利用GPS垂直位移反演区域陆地水储量变化的TSVD-Tikhonov正则化方法

钟波， 李贤炮， 李建成*， 汪海洪,2， 丁剑

1 武汉大学测绘学院， 武汉 430079 2 地球空间环境与大地测量教育部重点实验室， 武汉 430079 3 湖北珞珈实验室， 武汉 430079 4 中国测绘科学研究院， 北京 100830

0 引言

全球定位系统(Global Positioning System, GPS)作为现代大地测量的重要观测手段，被广泛应用于参考框架确定、板块构造动力学机制研究和地表形变监测等科学问题.根据质量负荷格林函数理论(Farrell, 1972)，地表质量负荷(如地表水、地下水和冰川等)的迁移与重新分布会导致地壳发生形变.例如，Heki(2001)研究发现日本东北地区地表积雪的季节性变化会使GPS站点产生抬升和沉降.由于地表形变可以被GPS以毫米级精度连续地进行监测，因此可以利用GPS形变观测数据独立地反演地表质量变化(Blewitt et al., 2001).特别是，很多国家和地区建立了密集的GPS连续运行台网对区域地表形变进行监测(姜卫平，2017)，这为反演精细的区域地表质量变化提供了有力的数据保障.

扣除大气和海洋质量变化以后，地表质量变化主要为陆地水储量变化(Terrestrial Water Storage Change，TWSC).TWSC是指储存在地表以及地下的全部水分，包括地表水、地下水、土壤水、树冠水以及积雪等，是水循环的重要组成部分(Rodell and Famiglietti, 1999; Cazenave and Chen, 2010; Rodell et al., 2018).由于GPS垂直位移相比水平位移能更准确地反映质量负荷变化信息(Wahr et al., 2013)，当前大多数研究是利用GPS垂直位移对区域TWSC进行反演.Argus 等(2014)利用密集的GPS垂直位移数据反演了美国加州地区的TWSC，结果表明其空间分辨率可达到～50 km，并且与重力恢复与气候实验卫星(Gravity Recovery and Climate Experiment，GRACE)观测结果及水文模型符合较好.随后，GPS被广泛用于反演不同地区的TWSC，如美国中西部地区(Borsa et al., 2014; Fu et al., 2015; Jin and Zhang, 2016; Argus et al., 2017)、中国西南地区(何思源等, 2018; Zhong et al., 2020; 成帅等, 2021; Jiang et al., 2021a,b; Shen et al., 2021)以及南美洲(Ferreira et al., 2019)等典型区域.其中，Borsa 等(2014)利用GPS垂直位移反演的TWSC研究了美国西部的干旱情况，结果表明GPS反演的水量流失总量与水文气象观测结果一致；Fu等(2015)利用GPS垂直位移反演了美国华盛顿和俄勒冈州的TWSC，结果显示GPS反演结果与GRACE及水文模型结果具有高度相关性；Jin和Zhang(2016)利用GPS垂直位移反演的TWSC有效监测了2012年美国西南部的干旱事件，表明GPS形变观测具有干旱指示器的作用；Argus等(2017)利用GPS垂直位移估算了2012—2015年美国加州山区持续干旱期间的水储量流失情况；何思源等(2018)利用GPS垂直位移反演了云南省TWSC的时空分布；Ferreira等(2019)探讨了利用每日间隔的GPS垂直位移反演南美地区TWSC的空间分辨率；Jiang等(2021a)利用每天的GPS垂直位移反演了云南省日间隔的TWSC，并追踪了极端天气事件导致的水储量变化；Shen 等(2021)提出了将随机森林算法和地壳负荷模型相结合的机器学习负荷反演方法，有效提高了利用稀疏GPS测站数据反演TWSC的精度.此外，利用GPS反演的TWSC还可作为GRACE及其继任者GFO(GRACE Follow-on)观测结果的有益补充，特别是可以有效弥补GRACE/GFO缺失月份和任务间隔期的TWSC信息(Fu et al., 2015；Zhong et al., 2020).

利用GPS垂直位移反演区域TWSC属于典型的病态问题，常规方法是基于Tikhonov正则化方法(Tikhonov, 1963)并利用二阶拉普拉斯算子作为正则化约束矩阵对病态问题进行求解(Argus et al., 2014; Fu et al., 2015; Jin and Zhang, 2016; 何思源等, 2018; Zhong et al., 2020; Jiang et al., 2021a,b; Shen et al., 2021)，或者是基于截断奇异值分解(Truncated Singular Value Decomposition，TSVD)的正则化方法求解病态问题(Lai et al., 2020).但这两种正则化方法各有优势，其中Tikhonov正则化是通过引入先验约束矩阵并结合正则化参数选取方法对病态问题进行求解，有效提高了反演结果的稳定性；而TSVD正则化是通过舍弃设计矩阵中贡献较小的奇异值并仅由观测数据进行独立求解，其反演结果不依赖于先验信息且计算简单.因此，通过组合TSVD和Tikhonov正则化方法(即TSVD-Tikhonov)可实现两者优势互补，即利用TSVD正则化舍弃小奇异值对反演结果的影响，并利用Tikhonov正则化引入先验约束以提高解的稳定性，进而得到比单独正则化解更稳定和可靠的反演结果.例如，Chen T Y等(2020)基于TSVD-Tikhonov正则化方法利用GRACE时变重力场模型位系数对青藏高原地区的地表质量变化进行估计，结果显示TSVD-Tikhonov正则化比单独利用TSVD或Tikhonov正则化的反演结果更优.

尽管TSVD-Tikhonov组合正则化方法是一种更优的病态问题求解方案，但其并未有效用于解决GPS反演区域TWSC的病态问题.本文以四川省为实验区，利用中国地壳运动观测网络(Crustal Movement Observation Network of China，CMONOC)发布的72个GPS测站的垂直位移数据，基于TSVD-Tikhonov正则化方法反演2010年12月至2021年2月的TWSC时间序列.首先，通过数值模拟对TSVD、Tikhonov和TSVD-Tikhonov正则化方法采用不同正则化参数选取策略进行TWSC反演分析，以验证TSVD-Tikhonov正则化方法的有效性.其次，基于TSVD-Tikhonov正则化方法利用实测的GPS垂直位移反演四川省的TWSC时间序列，并与JPL(Jet Propulsion Laboratory)、CSR(Center for Space Research)和GSFC(Goddard Space Flight Center)发布的GRACE/GFO RL06 版本的Mascon模型进行对比.最后，利用广义三角帽方法(Generalized Three-Cornered Hat，GTCH)融合不同类型的水文气象资料得到更为可靠的降水、蒸散发和径流数据，并根据水量平衡方程计算的四川省dTWSC/dt时间序列对GPS和GRACE/GFO反演结果进行验证.

1 理论与方法

1.1 负荷格林函数理论

根据弹性负荷理论(Farrell，1972)，地表质量负荷变化(如TWSC)引起的地球形变可以近似表示为弹性形变(包括垂直和水平方向).其中，垂直形变可以表示为质量负荷与垂直位移格林函数的卷积(Wahr et al., 2013; Jin and Zhang, 2016; Zhong et al., 2020)：

(1)

式中，U(φ)为垂直形变；ΔM为点质量负荷；R和Me分别为地球的半径和质量；hl为负荷Love数，本文采用Wang等(2012)的计算结果；Pl为l阶勒让德多项式；φ为点质量负荷与GPS测站之间的角距.

根据式(1)，GPS垂直位移与TWSC之间的观测方程可以表示为：

y=Ax+e,e～(0,σ2I),

(2)

式中，y为GPS垂直位移观测向量；A为格林函数设计矩阵；x为待求的TWSC向量，通常采用等效水高(Equivalent Water Height，EWH)表示；e和σ2分别是GPS垂直位移y的观测值残差向量和误差方差；I是与y相对应的单位矩阵.

1.2 正则化方法

由于相邻GPS测站的垂直位移观测值之间存在相关性，以及GPS测站个数通常远小于待估参数个数，这些都会导致式(2)求解的法方程矩阵条件数过大，因此利用GPS垂直位移反演区域TWSC属于典型的离散病态问题.以下简单介绍病态问题求解的Tikhonov和TSVD正则化方法，并给出两者组合的TSVD-Tikhonov正则化方法.

1.2.1 Tikhonov正则化

Tikhonov正则化方法是通过引入先验正则化约束矩阵对病态问题进行稳定求解.根据式(2)的观测方程，正则化约束求解TWSC向量x的目标函数为(Argus et al., 2014)：

(3)

式中，λ>0为正则化参数，其选取方法主要有L-curve法(Hansen, 1992)、广义交叉检验法(Generalized Cross Validation，GCV)(Golub et al., 1979)以及基于先验信息的均方根误差(Root Mean Square Error，RMSE)最小准则等；L为正则化约束矩阵，本文采用改进的正则化拉普拉斯矩阵(李贤炮等，2022)进行求解，该矩阵通过考虑边缘格网点与内部格网点之间的相关关系，可更好地抑制边缘效应的影响.于是，式(2)中TWSC参数向量的估值为：

(4)

需要说明的是，式(4)中GPS垂直位移的中误差σ通常难以准确获得，解算中可将σλ作为正则化参数进行估计.

1.2.2 TSVD正则化

TSVD正则化方法是通过对观测方程的设计矩阵进行奇异值分解，并利用贡献较大的奇异值及相应奇异向量对设计矩阵进行重构，再根据重构的观测方程独立求解待估参数.

对式(2)中格林函数设计矩阵A进行奇异值分解，可得(嵇昆浦和沈云中，2020)：

(5)

式中，Q=(q1,q2,…,qm)和V=(v1,v2,…,vn)分别为设计矩阵A的左、右奇异向量，m和n分别为观测值个数和待估参数个数；Σ=diag(σ1,σ2,…,σm)，σ1>σ2>…>σm>0为设计矩阵A的奇异值.

于是，由奇异值分解得到式(2)中TWSC参数向量的最小二乘估计解为：

(6)

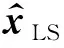
(7)

1.2.3 TSVD-Tikhonov正则化

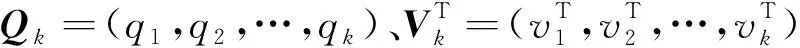
(8)

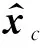
1.3 广义三角帽方法

广义三角帽方法(GTCH)最大的优点是可在缺少数据先验信息的情况下对多组数据集的不确定性进行评估(Tavella and Premoli, 1994; Galindo et al., 2001)，已被广泛用于估计不同GRACE时变重力场模型及陆面模型的不确定度(Long et al., 2017; 姚朝龙等，2019；Zhao et al., 2019).因此，本文采用GTCH方法对不同数据集(或模型)的不确定度进行估计，并根据估计的方差进行最优融合，进而得到更加可靠的结果.

针对不同的数据集{Xi,i=1,2,…,N}，其加权融合的结果可以表示为：

(9)

其中，pi为数据集Xi对应的权重，具体计算方法为：

(10)

式中，ωi为GTCH方法估计得到的数据集Xi的方差，具体计算方法参见姚朝龙等(2019)和Zhao 等(2019).

2 数值模拟

2.1 实验区概况

四川省位于我国西南地区，地处长江上游，界于北纬26°03′—34°19′和东经97°21′—108°12′之间，全省面积约为4.86×105km2，自然资源丰富，地形复杂多样，高差悬殊较大，地势呈西高东低的特点(见图1).四川省内气候温暖湿润，冬暖夏热，包含亚热带季风气候、高原山地气候以及高原高寒气候等多种气候类型，年平均气温约为16.4 ℃，多数地区的年降水量在900～1200 mm之间.在全球气候变暖的背景下，监测四川省TWSC的时空变化对于该地区的水循环研究及自然资源配置和经济发展具有重要意义.

为了更好的反演TWSC，并降低边缘效应的影响，本文将解算区域从四川省的边界向外扩展了2°，并使用了整个区域内共72个连续运行的GPS测站垂直位移数据进行计算.这些GPS测站的位置分布情况如图1所示，其中南部和东北部的测站相对密集，而西北部和东南部的测站相对稀疏，整个计算区域平均每10000 km2约有38.6个GPS测站，测站之间的平均距离约为169.6 km.

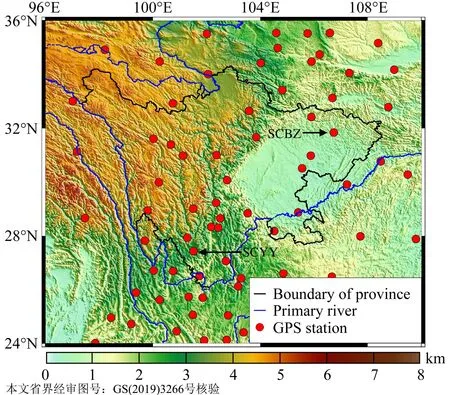
图1 实验区的地形及GPS测站位置分布Fig.1 Topography of the test area and distribution of GPS stations

2.2 不同正则化方法的模拟结果

为了验证TSVD-Tikhonov正则化方法的有效性，利用模拟的GPS垂直位移数据，基于TSVD、Tikhonov和TSVD-Tikhonov正则化方法采用不同的正则化参数选取策略进行反演.数值模拟中，将研究区域划分为0.5°×0.5°格网，以GLDAS(Global Land Data Assimilation Systems)水文模型(Rodell et al., 2004)计算的2005年1—12月的TWSC作为原始信号，根据式(1)模拟研究区域内72个GPS测站的垂直位移观测值，并在垂直位移数据中加入均值为0 mm、标准差为1 mm的高斯白噪声，然后分别由式(4)、式(7)和式(8)采用不同的正则化参数选取策略(RMSE最小准则、GCV法和L-curve法)反演TWSC，并将其与原始信号进行对比分析.

图2a和2b分别为基于Tikhonov和TSVD正则化方法采用不同的正则化参数选取策略反演的2005年1—12月的TWSC及与原始信号的区域平均时间序列比较.可以看出，Tikhonov和TSVD正则化方法的反演结果都能够与原始信号保持较好的一致性，但Tikhonov正则化对应的反演结果与原始信号更为接近，而TSVD的反演结果与原始信号的整体差异相对较大(如2005年9月)，这表明Tikhonov正则化相比TSVD正则化的反演结果更为稳定和可靠.

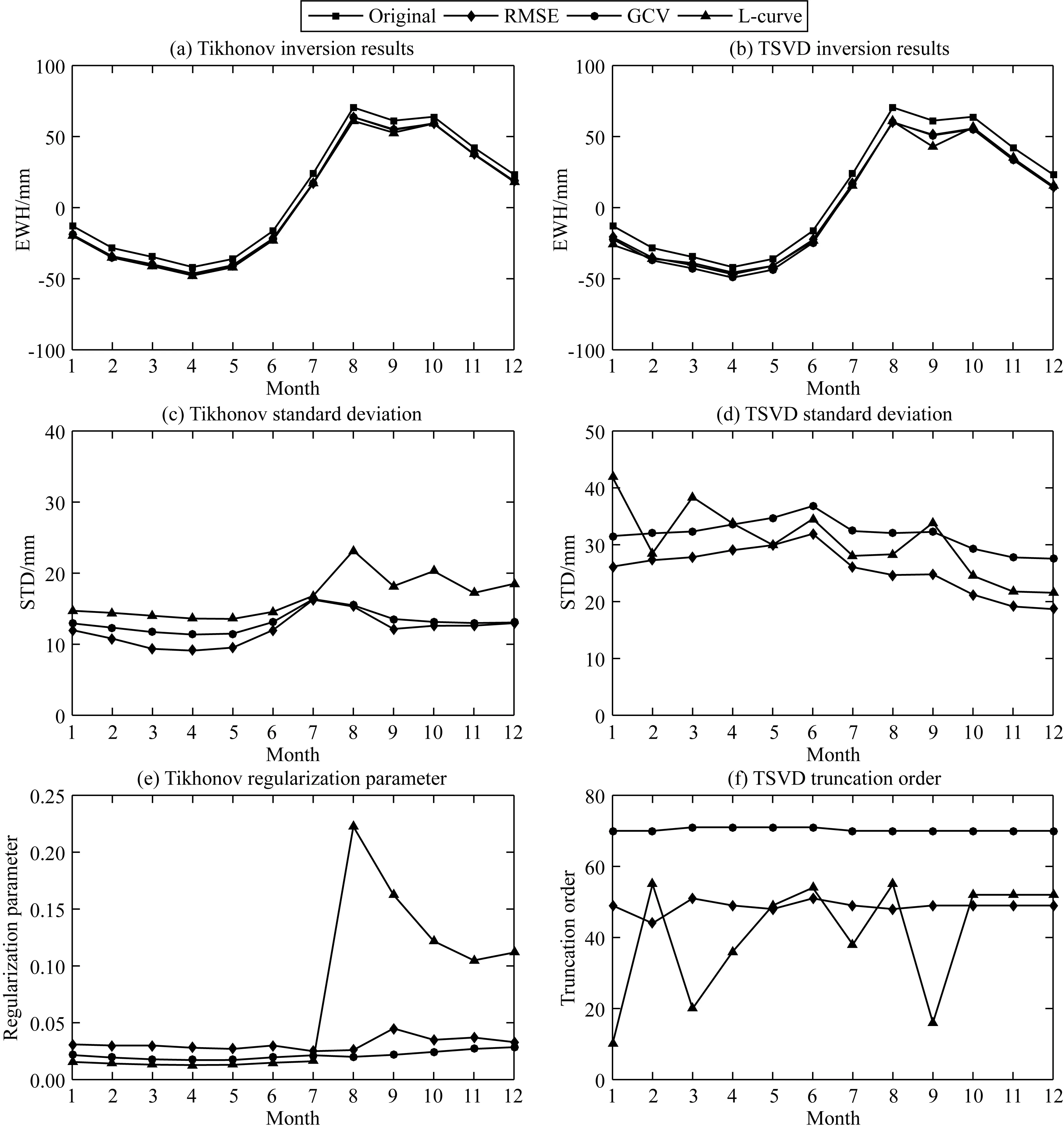
图2 基于TSVD和Tikhonov正则化由不同正则化参数选取方法反演的TWSC(a和b)及其与原始信号的差值标准差(c和d)和相应的最优正则化参数与截断阶数(e和f)Fig.2 TWSC solved by Tikhonov and TSVD regularizations through different regularization parameter selection methods (a and b), STD of differences between the estimated TWSC and original signal (c and d), and the corresponding optimal regularization parameters and truncation orders (e and f)

图2c和2d分别为基于Tikhonov和TSVD正则化方法由不同的正则化参数选取策略反演的TWSC与原始信号差值的标准差(Standard Deviation，STD).可以看出，在Tikhonov正则化的反演结果中，RMSE最小准则对应的STD最小，GCV法对应的STD次之，而L-curve法对应的STD最大；在TSVD正则化的反演结果中，RMSE最小准则对应的STD同样为最小，而L-curve法对应的STD在大多数月份小于GCV法对应的STD，但GCV法相比L-curve法对应的STD变化更为稳定.总体而言，TSVD正则化对应的STD均要大于Tikhonov正则化对应的STD，这也表明Tikhonov正则化比TSVD正则化的反演结果精度更高.

图2e和2f分别为Tikhonov和TSVD正则化采用RMSE最小准则、GCV法和L-curve法反演TWSC所选取的最优正则化参数和截断阶数.对于Tikhonov正则化而言，GCV法与RMSE最小准则确定的正则化参数更为接近，而L-curve法确定的正则化参数在8—12月出现较大差异，其对应的误差STD也相对较大(见图2c)，这是因为L-curve法有时难以准确获取最优的正则化参数；对于TSVD正则化，L-curve法与RMSE最小准则确定的最优截断阶数相近的月份更多，但L-curve法确定的最优截断阶数逐月变化差异较大，而GCV法确定的最优截断阶数的变化更为平稳.

为了对TSVD-Tikhonov正则化的截断阶数进行分析，图3a和3b分别给出了格林函数设计矩阵A的奇异值和不同截断阶数对应的累积贡献率，可知设计矩阵A的奇异值在40～50阶以后的变化趋于缓慢，其对应的累积贡献率在80%以上.例如，截断至44阶对应的累积贡献率达到了87.75%.

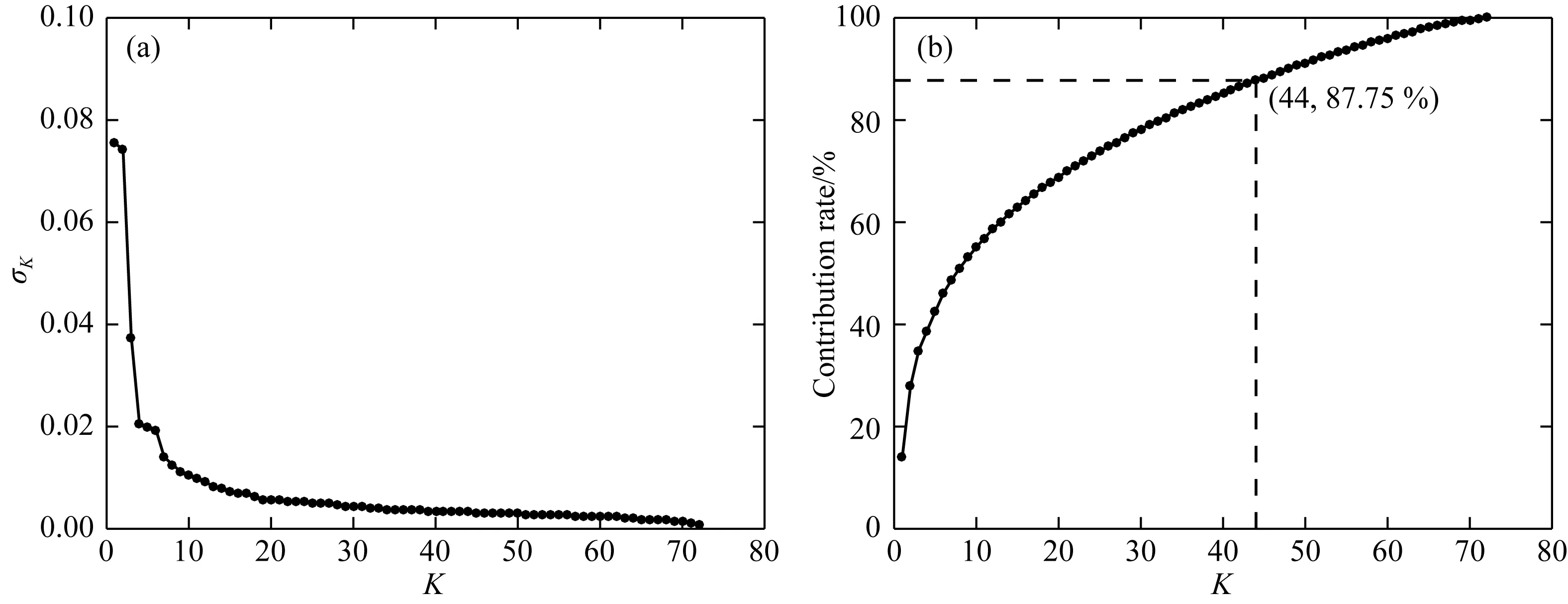
图3 设计矩阵奇异值(a)和不同截断阶数对应的累积贡献率(b)Fig.3 Singular values of design matrix (a) and their cumulative contribution ratio (b) with different truncation orders

由于Tikhonov正则化比TSVD正则化的反演结果更可靠(见图2)，因此图4a和4b以Tikhonov正则化反演结果作为参考，分别给出了Tikhonov正则化和采用不同截断阶数的TSVD-Tikhonov组合正则化反演结果对应的误差STD.图4a中矩形点线是Tikhonov正则化采用RMSE最小准则确定最优正则化参数的反演结果与原始信号差值的STD；圆形点线是TSVD-Tikhonov正则化采用RMSE最小准则选取TSVD截断阶数、GCV法确定Tikhonov最优正则化参数所对应的反演结果与原始信号差值的STD.可以看出，除个别月份(7月)以外，TSVD-Tikhonov正则化比Tikhonov正则化反演结果对应的STD更小，说明TSVD-Tikhonov正则化方法的反演结果更优.

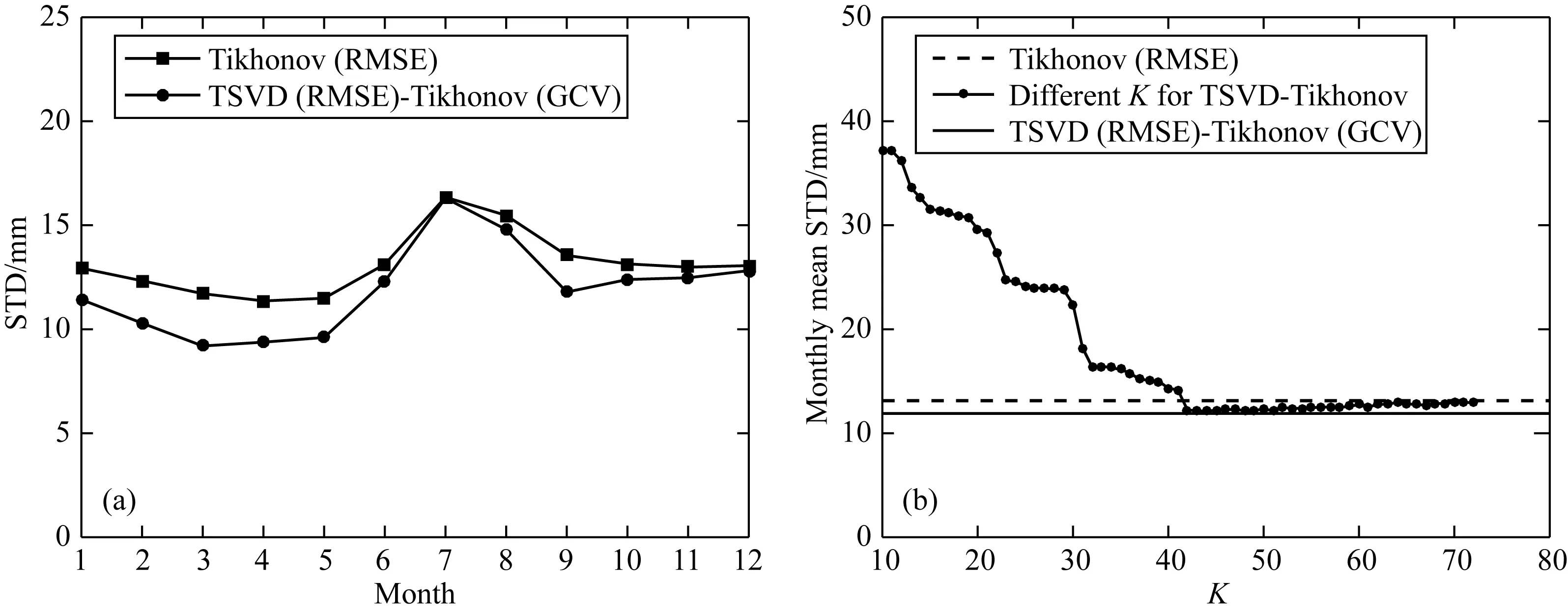
图4 Tikhonov正则化和不同截断阶数K的TSVD-Tikhonov正则化反演结果的误差STD(a)和月平均误差STD(b)Fig.4 STD (a) and monthly mean STD (b) of the errors of the inversion results based on Tikhonov regularization and TSVD-Tikhonov regularization with different truncation order K

图4b中虚线和实线分别为图4a中Tikhonov和TSVD-Tikhonov正则化反演结果对应STD的月平均值，而圆形点线则为不同截断阶数的TSVD-Tikhonov正则化反演结果对应的月平均STD值.可以看出，在截断阶数为42阶以后，TSVD-Tikhonov正则化比Tikhonov正则化反演结果对应的月平均STD更小，并且截断阶数为44阶时达到最优，相应的累积贡献率为87.75%(见图3b).而在TSVD-Tikhonov组合正则化过程中，每个月都以RMSE最小准则选取TSVD最优截断阶数，并采用GCV法确定最优正则化参数，其反演结果对应的月平均STD为最小(图4b中实线)，可认为是理论最优结果.

为了进一步评估TSVD-Tikhonov正则化方法的有效性，图5给出了TSVD、Tikhonov和TSVD-Tikhonov正则化反演的2005年1月至12月TWSC序列与原始信号差值STD的空间分布.可以看出，在整个四川省区域内，TSVD正则化反演结果的STD最大，平均STD为14.97 mm；Tikhonov正则化与TSVD-Tikhonov正则化对应的STD相对较小且总体接近，但在四川省东部Tikhonov正则化对应的STD比TSVD-Tikhonov正则化对应的STD更大，其相应的平均STD分别为7.03 mm和5.04 mm.也就是说，TSVD-Tikhonov正则化对应的平均STD在三者之中最小，即TSVD-Tikhonov正则化方法反演TWSC的精度最高.

图5 TSVD (a)、Tikhonov (b)和TSVD-Tikhonov (c)正则化反演的TWSC序列与原始信号差值STD的空间分布Fig.5 Spatial distributions of STD of the differences between the estimated TWSC series and original signal based on TSVD (a), Tikhonov (b), and TSVD-Tikhonov (c) regularizations

以上数值模拟结果表明，TSVD-Tikhonov正则化方法比单独利用TSVD或Tikhonov正则化方法反演的四川省TWSC的精度更高、稳定性也更好，初步验证了TSVD-Tikhonov组合正则化方法的有效性.需要指出的是，实测数据处理中无法获得可靠的先验信息由RMSE最小准则选取TSVD对应的最优截断阶数，因此在后续实测数据反演中以数值模拟得出的最优阶数(44阶)作为TSVD-Tikhonov正则化的截断阶数.同时，综合考虑GCV法和L-curve法的数值稳定性及反演精度(见图2)，在后续实测数据计算中采用GCV法确定最优正则化参数.

3 反演建模与结果分析

3.1 数据来源及预处理

3.1.1 GPS垂直位移数据

利用CMONOC的72个GPS测站(位置分布见图1)获取的2010年12月至2021年2月期间的垂直位移时间序列进行TWSC反演(数据下载自国家地震科学数据中心http:∥www.eqdsc.com).CMONOC提供的GPS单日位移时间序列相对于ITRF2008参考框架，是由GAMIT/GLOBK软件(10.4版)基于双差模型解算得到(详细说明参见官网数据处理手册).由于CMONOC发布的GPS位移时间序列已经扣除了固体潮、海潮以及极潮等的影响，因此获取的GPS垂直位移主要反映的是陆地水、非潮汐大气和海洋质量变化引起的垂直形变.此外，由于人类活动(Yao et al., 2020)、设备更换以及自然环境变化等因素的影响，GPS位移时间序列会存在数据跳跃和间断，因此需要对GPS垂直位移数据进行预处理，主要包括粗差探测和数据插值等.本文利用四分位粗差探测方法(Nikolaidis, 2012)剔除粗差，并采用克里金-卡尔曼滤波方法(Liu et al., 2018)对缺失的垂直位移数据进行插值补齐.图6给出了四川巴中(SCBZ)和四川盐源(SCYY)两个测站(位置见图1)的垂直位移时间序列在滤波前后的对比，图中显示滤波处理可以很好地去除高频噪声并填补缺失的数据.

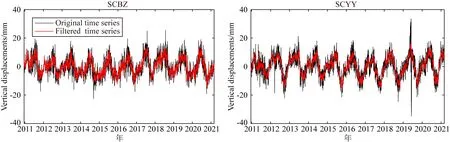
图6 SCBZ和SCYY测站的垂直位移时间序列滤波前后比较Fig.6 Comparisons of the vertical displacement time series at SCBZ and SCYY stations before and after filtering

另外，GPS垂直位移时间序列的长期趋势中包含了由地表质量变化、冰川均衡调整(Glacial Isostatic Adjustment，GIA)和板块运动等地球物理现象的综合贡献，但却难以将GIA和板块运动等引起的长期趋势准确地分离出来.考虑到研究区域的地表质量变化以季节性特征为主，因此在GPS垂直位移时间序列的预处理过程中扣除了长期趋势项，保留了周年和半周年变化信号.此外，为了最终反演得到TWSC序列，利用非潮汐大气与海洋去混频产品(Atmosphere and Ocean De-aliasing Level-1B, AOD1B)RL06版本扣除了GPS垂直位移中由非潮汐大气和海洋效应导致的地表形变影响.同时，为了与GRACE/GFO Mascon模型的时间尺度保持一致，本文将GPS垂直位移数据取月平均，然后用于TWSC的反演.

3.1.2 GRACE/GFO Mascon模型

为了对GPS反演结果进行比较，采用CSR(Save et al., 2016)、JPL(Watkins et al., 2015; Wiese et al., 2016)和GSFC(Loomis et al., 2019)发布的GRACE/GFO RL06版本的Mascon模型，分别计算了四川省2010年12月至2017年6月和2018年6月至2021年2月期间的TWSC时间序列.需要说明的是，Mascon模型通过采用约束方法对GRACE/GFO观测中含有的南北条带误差进行抑制，具有更高的空间分辨率，因此可以使用Mascon模型直接计算TWSC，并不需要对其进行滤波处理和信号泄漏改正.此外，由于GRACE/GFO反演的低阶项系数存在较大的不确定性，Mascon模型中对应的C20和C30(只针对GFO解)项已使用卫星激光测距(Satellite Laser Ranging，SLR)的估计结果进行了替换，并且地心运动导致的一阶项变化和GIA等效应也进行了相应改正，参见Save 等(2016)和Watkins 等(2015).

3.1.3 降水、蒸散发和径流数据

利用不同类型水文气象资料得到的降水、蒸散发和径流数据对GPS和GRACE/GFO反演结果进行检验.这些资料包括国家气象信息中心NMIC(National Meteorological Information Center)提供的地面降水月值0.5°×0.5°格网数据集V2.0(http:∥data.cma.cn/)；热带降雨测量任务TRMM(Tropical Rainfall Measurement Mission)(Huffman et al., 2007)提供的月值0.25°×0.25°格网降水数据(https:∥disc.gsfc.nasa.gov/datasets/TRMM_3B43_7/summary)；全球陆地蒸散发模型GLEAM(Global Land Evaporation Amsterdam Model)(Miralles et al., 2011; Martens et al., 2017)提供的月值0.25°×0.25°格网蒸散发数据(https:∥www.gleam.eu/)；英国国家大气科学中心NCAS(National Centre for Atmospheric Science)研制的气候产品CRU(Climatic Research Unit)计算的月值0.5°×0.5°格网降水和蒸散发数据(https:∥crudata.uea.ac.uk/cru/data/hrg/)；以及GLDAS的三个陆面模型Noah、CLSM和VIC(Rodell et al., 2004)计算的月尺度降水、蒸散发和径流数据(https:∥earthdata.nasa.gov/search?q=GLDAS)，其中Noah数据为0.25°×0.25°格网，CLSM和VIC数据为0.5°×0.5°格网.

对于一个特定的区域，其水循环主要是由降水、蒸散发和径流控制(Chen J L et al., 2020).于是，区域内的水量平衡方程可以表示为(Famiglietti et al., 2011; 李琼等，2013)：

(11)

式中，P为降水，ET为蒸散发，R为径流，dS/dt为TWSC关于时间t的一阶导数，即为dTWSC/dt.同时，由GPS或GRACE/GFO反演的TWSC序列计算dS/dt的公式可表示为：

(12)

式中，dSt为利用GPS或GRACE/GFO反演的连续两个月之间的TWSC，这里dt为1个月.

因此，可以采用水量平衡方程计算的月平均dTWSC/dt对GPS和GRACE/GFO计算的月平均dTWSC/dt进行检验.但水量平衡方程(式(11))计算的月平均dS/dt对应的时间为月中，而式(12)采用中心差分计算的GPS和GRACE/GFO月平均dSt/dt对应的时间为月初或月末.为了使两者在时间上保持一致，本文首先采用Landerer 等(2010)提出的时间序列滤波方法分别对水量平衡方程中的降水、蒸散发和径流数据进行滤波处理，即：

(13)

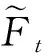
3.2 棋盘测试结果

利用GPS垂直位移反演TWSC的分辨率和可靠性还与计算区域内测站的数量及空间分布有关.因此，以下通过棋盘测试分析现有72个GPS测站分布对研究区内陆地水储量的恢复能力.将研究区域划分为0.5°×0.5°规则格网，棋盘信号采用2°×2°的EWH表示，如图7a所示，其中白色和棕色棋盘分别表示0 mm和300 mm的EWH信号.利用图7a中的棋盘信号模拟了72个GPS测站的垂直位移，然后将其反演得到如图7b所示的EWH空间分布.从图7b可以看出，川东盆地和川南地区的GPS测站相对密集，其反演结果对原始信号的恢复较好；而川西北地区的GPS测站分布相对稀疏，其反演结果对原始信号的恢复较差.总体而言，本文采用的72个GPS测站数据，它们之间的平均测站距离约为169.6 km，可以较好地恢复四川省内约2°×2°空间分辨率的TWSC信号.

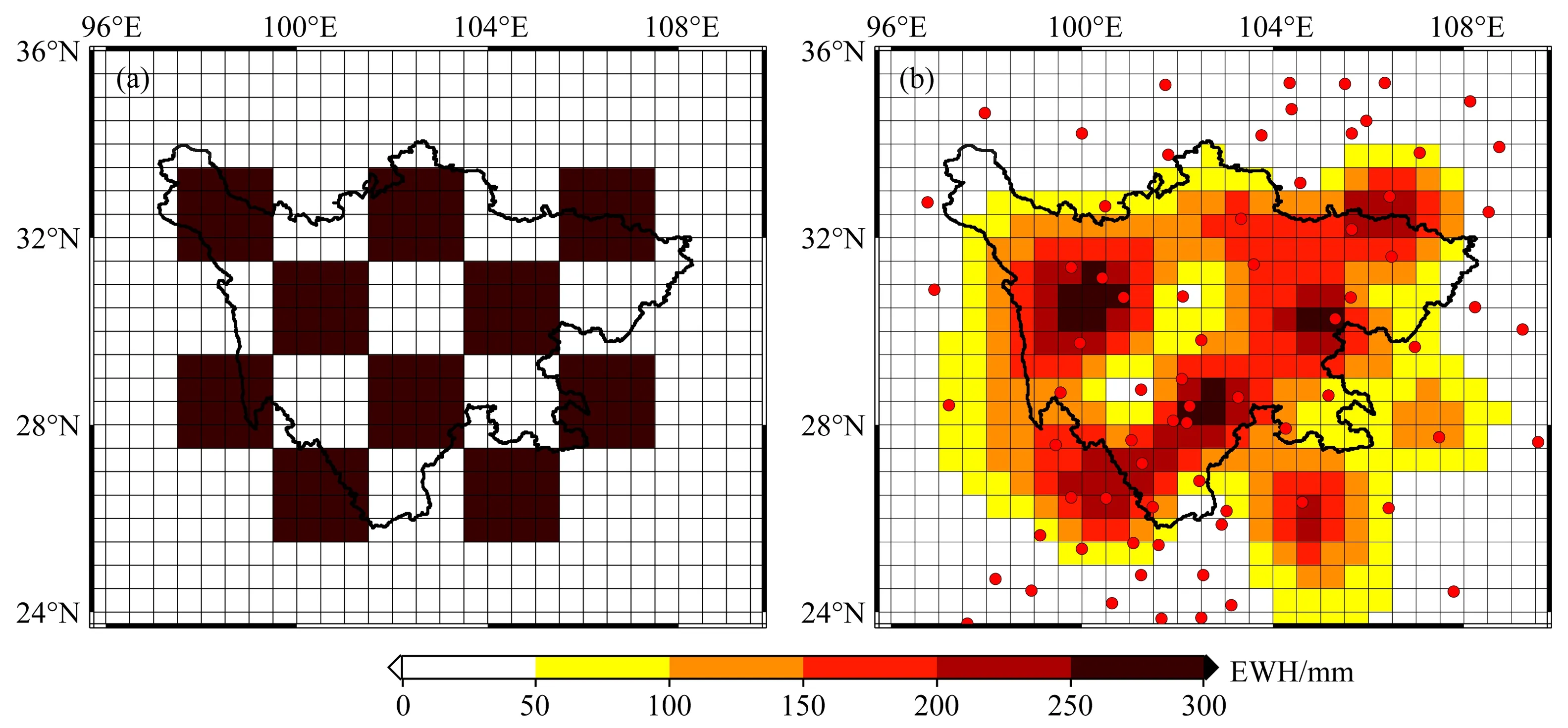
图7 72个GPS测站恢复EWH信号的棋盘测试(a) 原始信号； (b) 反演结果.Fig.7 Checkerboard test of EWH signal recovered from 72 GPS stations(a) Original signal; (b) Inversion result.

3.3 与GRACE/GFO反演结果对比

图8为官方机构(JPL、CSR和GSFC)发布的GRACE/GFO Mascon模型与GPS反演的TWSC在2010年12月至2021年2月期间的周年振幅空间分布.其中，图8a—c中的周年振幅为同时拟合GRACE和GFO数据的结果，图8d中GPS反演的TWSC采用了截断阶数为44阶的TSVD-Tikhonov组合正则化方法，并采用GCV方法确定最优正则化参数.

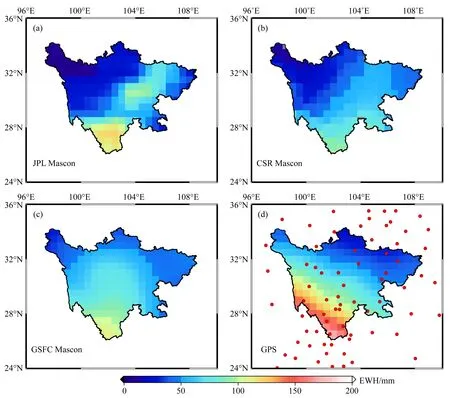
图8 GRACE/GFO Mascon模型(JPL、CSR和GSFC)与GPS垂直位移反演的TWSC周年振幅空间分布Fig.8 Spatial patterns of annual amplitudes for TWSC derived from GRACE/GFO Mascons (JPL, CSR, and GSFC) and GPS vertical displacements

从图8可以看出，JPL和CSR Mascon模型得到的TWSC周年振幅的空间分布较为一致，其在川东盆地的信号较强，川西高原的信号较弱，并且JPL比CSR反演结果的信号更强；而GSFC Mascon模型与GPS反演结果的周年振幅空间分布在总体上更为接近，它们在川西南山地的信号较强，而在东北部地区的信号较弱，并且GPS比GSFC反演结果的信号更强.总体上看，GPS反演结果与GRACE/GFO Mascon模型的周年振幅保持了较好的一致性，但GPS反演的TWSC信号振幅更强，这是由于基于地基观测的GPS垂直形变数据对局部水质量负荷变化更为敏感，而GRACE/GFO反演结果的空间分辨率有限(～300 km)，受到信号泄漏及混频效应的影响，其对大尺度的TWSC估计更为准确.同时，GPS和GRACE/GFO观测数据误差来源及数据处理策略的不同也是导致两者反演结果具有差异的一个重要原因.另外，与Jiang 等(2021b)利用GPS反演的四川省TWSC的周年振幅相比，本文反演结果的空间分布特征与其总体接近，但振幅量级相对偏小.引起该差异的主要原因可能有两方面：一方面是由于不同的GPS解算软件和解算策略会引起反演结果的差异，另一方面是本文反演TWSC所采用的四川省内的GPS测站数有限且分布更为稀疏，进而影响了TWSC信号的恢复性能.

图9为GPS反演的TWSC、GRACE/GFO Mascon模型(JPL、CSR和GSFC)及GTCH方法融合的Mascon模型(定义为GTCH-TWSC)在2010年12月至2021年2月之间的时间序列变化.可以看出，GPS和GRACE/GFO反演结果总体保持较好的一致性，并且都很好地反映了四川省TWSC明显的季节性变化特征.此外，利用GPS反演的TWSC时间序列的振幅总体大于GRACE/GFO反演结果，并且能够很好地填补GRACE和GFO任务间隔期的数据空白.需要指出的是，图9还显示出GPS反演结果在2011、2012和2017等年份的年初或年终存在异常信号，且比GRACE/GFO反演结果更敏感，这可能是由于GPS时间序列中仍然含有未被模型化的虚假信号所引起，如交点年误差(Fu et al., 2015; 何思源等，2018).

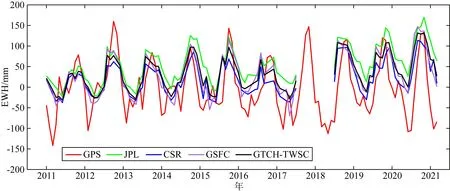
图9 GRACE/GFO Mascon模型(JPL、CSR和GSFC)及其融合模型(GTCH-TWSC)与GPS垂直位移反演的TWSC时间序列比较Fig.9 Comparisons of TWSC time series derived from GRACE/GFO Mascons (JPL, CSR, and GSFC) and their fusion model (GTCH-TWSC), and GPS vertical displacements

由于GPS垂直位移时间序列在预处理中扣除了长期趋势项，为了与其保持一致性，将GRACE/GFO反演结果同样扣除趋势项，然后统计两者的相关性和差值STD.表1为去掉趋势后GRACE/GFO Mascon模型(JPL、CSR和GSFC)及其GTCH融合模型(GTCH-TWSC)与GPS反演的TWSC时间序列的相关系数和差值STD统计.对比表1中三个Mascon模型的统计结果可知，JPL与GPS反演结果的相关性最好且STD最小，GSFC次之，而CSR对应的相关性和STD略差.而GTCH融合模型GTCH-TWS与GPS反演结果的相关性和差值STD均为最好，这说明通过GTCH方法估计的误差方差对不同模型进行加权得到的融合模型GTCH-TWS更加可靠，其与GPS反演结果的一致性也更好.

表1 GRACE/GFO Mascon模型(JPL、CSR和GSFC)及其融合模型(GTCH-TWSC)与GPS反演的TWSC时间序列去除线性趋势后的相关系数和差值STD统计Table 1 Correlation coefficients and STD of the differences between TWSC time series derived from GPS and GRACE/GFO Mascons (JPL, CSR, and GSFC) and their fusion model (GTCH-TWSC) after removing linear trends

表2给出了GPS反演的TWSC、GRACE/GFO Mascon模型(JPL、CSR和GSFC)及其融合模型GTCH-TWSC分别在2010年12月—2021年2月、2010年12月—2017年6月和2018年6月(GPS为2017年7月)—2021年2月等三个时间段对应时间序列的周年振幅、相位和线性趋势统计.由表2可知，GPS反演的TWSC时间序列在三个时段的周年振幅均大于GRACE/GFO结果，这是因为GPS反演的空间分辨率更高，并且地基GPS对局部范围的短波信号更为敏感.对于周年相位，GPS和GRACE/GFO反演结果的一致性较好，不同时段內各种结果的相位差异小于半个月.对于线性趋势，各种Mascon模型及其融合模型均呈现增长趋势，其中JPL反演结果的增长趋势最为明显，CSR与GSFC反演结果的增长趋势相当.相反，GPS反演结果在以上三个时段均呈现下降趋势.其主要原因是，本文对GPS垂直位移时间序列做了去趋势处理(用于扣除GIA和板块构造运动导致的长期趋势)，进而影响了GPS反演结果对应线性趋势的准确性.需要指出的是，四川省TWSC主要为季节性变化，其趋势变化较小，因而各种结果估计趋势的不确定度也较大.

表2 GPS、GRACE/GFO Mascon模型(JPL、CSR和GSFC)及其融合模型(GTCH-TWSC)估计的TWSC时间序列的周年振幅、相位和线性趋势统计Table 2 Annual amplitudes, phases, and linear trends of TWSC time series estimated by GPS, GRACE/GFO Mascons (JPL, CSR, and GSFC) and their fusion model (GTCH-TWSC)

3.4 水文气象数据验证结果

图10为采用不同类型水文气象资料计算的四川省2011—2021年的月平均降水、蒸散发和径流时间序列.其中，图10a为不同数据源计算的月平均降水变化时间序列，可以看出不同类型降水数据的一致性较好，其周年振幅约为200 mm/month，但在降水量达到峰值的月份仍有一定的差异(如2012、2018和2020年的7—9月).图10b为不同数据源计算的月平均蒸散发变化时间序列，其周年振幅约为100 mm/month，但不同类型的蒸散发数据在相位和振幅上都存在较大的差异.图10c为GLDAS三个陆面模型(Noah、CLSM和VIC)计算的月平均径流变化时间序列，相比于该区域的月平均降水和蒸散发变化，其月平均径流变化的量级略小，振幅在100 mm/month以内，并且三个陆面模型计算的径流变化之间也存在较大的差异.

由于各种类型水文气象资料的精度和可靠性不同，为了降低不同数据源计算的降水、蒸散发和径流变化的差异影响，本文采用GTCH方法对各类数据进行融合，得到更为可靠的降水、蒸散发和径流数据，以便更好地对GPS和GRACE/GFO反演的dTWSC/dt进行验证.

图11a是利用图10a—c中不同类型的月平均降水(P)、蒸散发(ET)和径流(R)时间序列，采用GTCH方法融合得到的降水(GTCH-P)、蒸散发(GTCH-ET)和径流(GTCH-R)数据.图11b是利用融合后的GTCH-P、GTCH-ET和GTCH-R由水量平衡方程(式(11))计算的dTWSC/dt序列(记为PER-dS/dt)，以及GPS反演的TWSC和GRACE/GFO融合模型GTCH-TWSC由式(12)计算的dTWSC/dt序列(分别记为GPS-dS/dt和GRACE/GFO-dS/dt).其中，PER-dS/dt序列采用了式(13)进行滤波处理，以保持其与GPS-dS/dt和GRACE/GFO-dS/dt序列的时间同步.从图11b可看出，PER-dS/dt序列与GPS-dS/dt和GRACE/GFO-dS/dt序列的季节性变化具有很好的一致性，但GPS-dS/dt序列的振幅略大于PER-dS/dt和GRACE/GFO-dS/dt序列，并且GPS-dS/dt和GRACE/GFO-dS/dt序列的逐月变化差异较大.

图10 不同类型水文气象数据计算的四川省月平均降水、蒸散发和径流变化(2011—2021年)Fig.10 Monthly average precipitation, evapotranspiration, and runoff changes of Sichuan Province derived from different hydrometeorology datasets (from 2011 to 2021)

图11 (a)GTCH方法融合后的降水、蒸散发和径流月平均时间序列； (b)和(c) 分别为平滑前后的PER-dS/dt、GPS-dS/dt和GRACE/GFO-dS/dt时间序列Fig.11 (a) Monthly average precipitation, evapotranspiration, and runoff time series fused by GTCH method; (b) and (c) are the PER-dS/dt, GPS-dS/dt, and GRACE/GFO-dS/dt time series before and after smoothing

为了避免各类数据中高频噪声的影响，并更为直观的分析以上三种dTWSC/dt时间序列的季节性变化特征，以及考虑到时间序列中可能存在的半周年信号，分别对PER-dS/dt、GPS-dS/dt和GRACE/GFO-dS/dt序列做5个月的滑动平均处理(Jiang et al., 2017)，其结果如图11c所示.可以看出，平滑后的PER-dS/dt、GPS-dS/dt和GRACE/GFO-dS/dt序列具有更好的一致性，但平滑后的GPS-dS/dt序列的振幅略大于平滑后的PER-dS/dt和GRACE/GFO-dS/dt序列.此外，PER-dS/dt序列相比GPS-dS/dt和GRACE/GFO-dS/dt序列有明显的相位滞后(统计结果见表3).

表3给出了GTCH方法融合的降水、蒸散发和径流月平均序列，GPS反演的TWSC序列(GPS-TWSC)和GRACE/GFO融合模型GTCH-TWSC(GRACE/GFO-TWSC)，以及PER-dS/dt、GPS-dS/dt和GRACE/GFO-dS/dt序列平滑前后计算的周年振幅和相位统计值.图12给出了平滑前后的GPS-dS/dt和GRACE/GFO-dS/dt序列与PER-dS/dt序列之间的散点图分布及相关系数和差值STD统计.

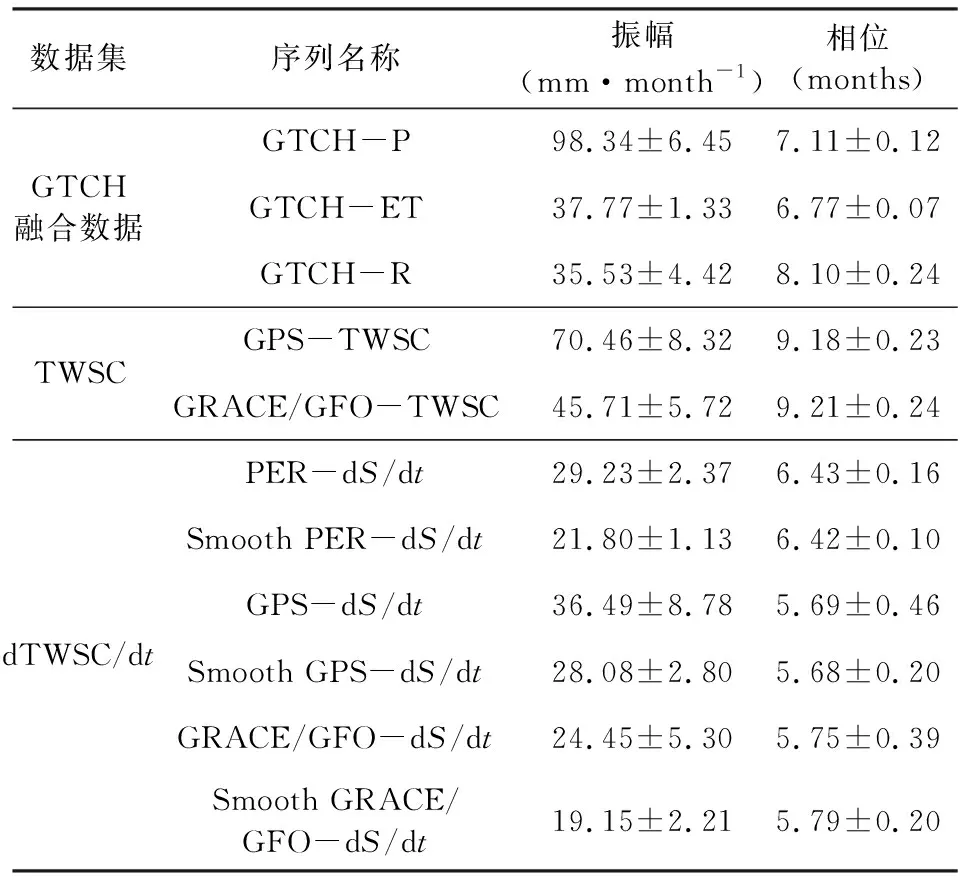
表3 不同类型时间序列数据的周年振幅和相位统计Table 3 Statistics of annual amplitudes and phases for the different types of time series datasets

由表3可知，GPS-TWSC和GRACE/GFO-TWSC序列比降水、蒸散发和径流数据的相位滞后了约1～2个月，这是因为TWSC是降水、蒸散发和径流变化的综合反映，这三者需要经过复杂的水动力学过程及时间变化才能转化为TWSC.比较不同的dTWSC/dt序列可以看出，平滑前后GPS-dS/dt的振幅均为最大，PER-dS/dt的振幅次之，而GRACE/GFO-dS/dt的振幅最小.此外，平滑前后各种序列的相位几乎保持不变，但与PER-dS/dt序列相比，GPS-dS/dt与GRACE/GFO-dS/dt序列的相位更为一致.

从图12可以看出，对于未平滑的结果，GPS-dS/dt和GRACE/GFO-dS/dt序列与PER-dS/dt序列的相关系数分别为0.53和0.73，差值STD分别为43.82 mm和18.37 mm，如图12a和b所示.而平滑以后(见图12c和d)，GPS-dS/dt和GRACE/GFO-dS/dt序列与PER-dS/dt序列的相关系数分别为0.78和0.87，差值STD分别为15.01 mm和8.44 mm.也就是说，平滑后GPS-dS/dt和GRACE/GFO-dS/dt序列与PER-dS/dt序列的差值STD明显减小，相关性有了显著提高(特别是GPS-dS/dt序列).但与GRACE/GFO-dS/dt序列相比，平滑前后GPS-dS/dt与PER-dS/dt序列之间的差异更大.

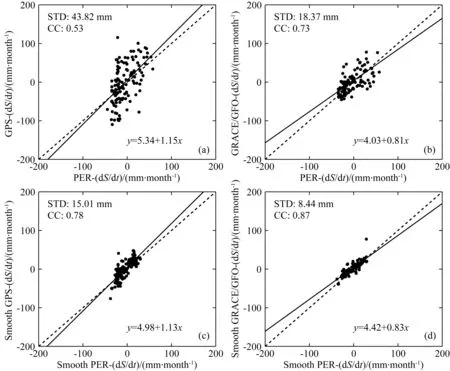
图12 平滑前后GPS-dS/dt和GRACE/GFO-dS/dt序列与PER-dS/dt序列之间的散点图及相关系数(CC)和差值STD比较Fig.12 Comparisons of scatter plot, correlation coefficient (CC), and STD of the differences between GPS-dS/dt, GRACE/GFO-dS/dt and PER-dS/dt series before and after smoothing

分析其原因，一方面考虑到地基GPS垂直形变数据对局部水质量负荷变化更敏感，其反演结果的幅度变化更大，进而引起GPS-dS/dt与PER-dS/dt序列之间的差值STD较大.另一方面，不同数据源计算的蒸散发和径流数据之间存在明显的差异(见图10b和c)，其GTCH融合结果的不确定度也相对较大，导致PER-dS/dt序列也存在较大的不确定性.考虑到不同源的降水数据差异较小(见图10a)，具有更好的可靠性，为此进一步分析了GPS和GRACE/GFO反演结果与GTCH融合的降水序列(GTCH-P)之间的相关性，结果显示GPS反演的TWSC序列与GTCH-P序列经5个月滑动平均处理前后的相关系数分别为0.55和0.85，而GRACE/GFO融合序列GTCH-TWSC与GTCH-P序列在平滑前后的相关系数分别为0.52和0.72，这说明GPS相比GRACE/GFO观测结果对降水变化的响应更为敏感，再次印证了其对局部水质量负荷变化的感应能力更强.以上分析表明，GPS和GRACE/GFO在监测TWSC方面各有优势，但由于GPS垂直位移对局部水质量负荷变化更为敏感，因此可作为GRACE/GFO反演区域TWSC的有益补充.

4 结论

本文研究了基于TSVD-Tikhonov组合正则化方法求解GPS垂直位移反演TWSC的病态问题，并通过数值模拟验证了其有效性.利用CMONOC发布的72个GPS测站的垂直位移数据反演了四川省的TWSC时间序列，并与官方机构(JPL、CSR和GSFC)发布的GRACE/GFO Mascon模型进行对比.同时，利用水文气象资料由水量平衡方程计算的dTWSC/dt序列对GPS反演结果进行验证.主要结论如下：

(1)利用模拟的72个GPS测站的垂直位移数据反演四川省TWSC，结果表明：采用不同的正则化参数选取策略(RMSE最小准则、GCV法和L-curve法)，TSVD-Tikhonov正则化反演的TWSC比单独使用TSVD或Tikhonov正则化的反演结果具有更高的精度和稳定性；TSVD、Tikhonov和TSVD-Tikhonov正则化方法反演2005年1月至12月的TWSC时间序列与原始信号差值的平均STD分别为14.97 mm、7.03 mm和5.04 mm.

(2)采用棋盘测试分析了现有72个GPS测站恢复四川省TWSC信号的能力，并利用实测的GPS测站垂直位移数据反演了四川省2010年12月至2021年2月的TWSC时间序列，结果表明：现有72个测站可以较好地恢复四川省内2°×2°空间分辨率的TWSC信号；基于TSVD-Tikhonov组合正则化由GPS反演的TWSC与GRACE/GFO Mascon模型(JPL、CSR和GSFC)及其GTCH融合模型的空间分布特征及季节性变化符合较好，并且GPS反演结果与GTCH融合模型更为一致；GPS反演的TWSC信号振幅比GRACE/GFO Mascon模型更强，这是由于地基GPS垂直形变观测数据对局部水质量负荷变化更为敏感，而GRACE/GFO反演的空间分辨率约为300 km，受到信号泄漏的影响，其对大尺度的TWSC估计更为准确.

(3)采用GTCH方法融合不同类型的降水、蒸散发和径流数据，根据水量平衡方程计算的dTWSC/dt序列(PER-dS/dt)对GPS反演结果(GPS-dS/dt)和GRACE/GFO Mascon模型融合结果(GRACE/GFO-dS/dt)进行验证，结果显示：GPS-dS/dt和GRACE/GFO-dS/dt序列与PER-dS/dt序列具有较好的一致性，平滑后GPS-dS/dt和GRACE/GFO-dS/dt序列与PER-dS/dt序列的相关系数分别为0.78和0.87，差值STD分别为15.01 mm和8.44 mm；GPS反演的TWSC序列和GRACE/GFO融合序列(GTCH-TWSC)与降水融合序列(GTCH-P)在平滑后的相关系数分别为0.85和0.72，说明GPS相比GRACE/GFO对降水变化的响应更为敏感.总体上讲，GPS和GRACE/GFO反演TWSC各有优势，但GPS观测对局部水质量负荷变化的感应能力更强，因此可作为GRACE/GFO反演区域TWSC的有益补充.

(4)TSVD-Tikhonov正则化方法有效提高了利用GPS垂直位移反演区域TWSC的精度和可靠性，但在实际应用中如何快速有效地选取最优截断阶数和最优正则化参数还需要深入探讨.同时，本文反演四川省TWSC采用的GPS测站分布较为稀疏，导致TWSC信号的恢复能力有限，后续可采用更为密集的GPS测站数据进行反演与验证.此外，有效分离GPS垂直位移时间序列中非水文负荷因素(如人类活动、GIA或板块构造运动等)导致的形变，并准确估计GPS反演的TWSC的长期趋势仍是一项具有挑战性的课题.

致谢感谢国家地震科学数据中心提供的CMONOC GPS垂直位移数据，JPL、CSR和GSFC提供的GRACE/GFO Mascon模型，NMIC和TRMM提供的降水数据，GLEAM提供的蒸散发数据，NCAS提供的降水和蒸散发数据，以及GLDAS提供的降水、蒸散发和径流数据.感谢三位匿名审稿专家对本文提出的宝贵修改意见和建议.