《复数的乘、除运算》教学设计
2023-03-16俞红玉黑龙江省哈尔滨市方正县第一中学校
俞红玉 黑龙江省哈尔滨市方正县第一中学校
●创新整合点
①利用PowerPoint制作多媒体课件,使课堂生动灵活,结尾简介“复数”这个神奇而又充满魅力的“诡辩量”—i,激发学生的学习兴趣,对学生进行德育渗透,从而让学生对科学未知充满好奇,让学生有勇气去质疑去挑战并积极地去探索宇宙的奥秘。
②利用电子白板制作游戏环节,使课堂氛围活跃,提高学生的课堂参与度,直观呈现学生学习效果,提高课堂效率。
③设计“我是小老师”环节,突破学生的固定思维模式,从“我是出题人”的角度出发,先是怎样把复数这部分知识学得更扎实、牢固,然后再能力提升,充分体现了学以致用。
●教材分析
本节课选自人民教育出版社出版的《普通高中教科书数学必修第二册(A版)》第七章第二节第二课时《复数的乘、除运算》,依据新课改新大纲要求,复数四则运算是本章知识的重点。主要内容是复数的乘、除运算。学生的知识基础是已经学习了复数的概念和坐标表示,在第二节第一课时,介绍了复数代数形式的加、减的运算法则,同时指出了复数加法、减法的几何意义,复平面上两点间的距离公式,沟通了“数与形”之间的联系,提供了用“形”来帮助处理“数”和用“数”来帮助处理“形”的工具。
在这节内容中,类比多项式的乘法法则,可把复数代数形式a+bi看成由a和bi两个非同类项组成,这样,多项式的运算法则几乎可以全部搬过来照用不误,于是复数就与多项式、方程联系起来,从而能帮助解决一些多项式中的因式分解、解方程等数学问题。新教材降低了对复数的要求,只要求学习复数的概念、复数的代数形式及几何意义、加减乘除运算及加减的几何意义。
通过本节课对学生渗透数形结合的数学思想,渗透化归的思想,将实数的运算通性、通法扩充到复数,是对数学知识的一种创新,有利于培养学生的学习兴趣和创新精神。所以,《复数的乘、除运算》一课的编排有着重要的意义。
●学情分析
高一学生知识经验与学习经验较为丰富,已具有类比知识点的学习方法。
●教学重难点
重点:复数代数形式的乘、除法的运算法则及其运算律。
难点:复数除法的运算法则。
●教学目标
知识与技能目标:理解并掌握复数的代数形式的乘法与除法运算法则。
过程与方法目标:在问题探究过程中,体会和学习类比等数学思想方法,感悟运算形成的基本过程。
情感态度与价值观目标:培养类比思想和逆向思维;通过复数的乘除法的学习,体会实虚数的矛盾和统一,加深对数学的情感认识。
数学核心素养:①数学抽象:复数乘法、除法运算法则;②逻辑推理:复数乘法运算律的推导;③数学运算:复数四则运算;④数学建模:结合实数范围内求根公式和复数四则运算,解决复数范围内的方程根问题。
●教学环境与准备
教学环境:多媒体教室、宽带网络、seewo触控一体机。
课堂准备:教材、练习本、笔等课堂用品。
●教学过程
1.复习回顾,引入新课
师:各位同学,大家好。今天这节课我们将探讨复数的乘法、除法运算。经过前面的学习,我们了解了复数的概念,以及复数加减法运算及其几何意义。复数的加法和减法法则,类似多项式的加减法,是将复数的实部与实部、虚部与虚部分别相加减。从几何意义的角度出发,复数的加法可以按照向量的加法(平行四边形法则)来进行,复数的减法可以按照向量的减法(三角形法则)来进。一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数。通过上节课的探究我们发现,复数的加减法与实数中多项式的加减法类似,那么,复数的乘除运算,是否也有这个规律呢?接下来让我们一起来探究一下。
设计意图:复习复数的加减法运算及其几何意义相关知识,通过复数加减法运算与实数运算的对比,引出复数乘除法的运算法则。
2.新课探究
(1)复数的乘法法则
师:我们规定,复数的乘法法则如下:设z1=a+bi,z2=c+di(a,b,c,d∈R),那么它们的积z1z2=(a+b i)(c+di)=ac+adi+bci+bdi2=(acbd)+(ad+bc)i。
根据复数的乘法法则,请思考并探讨以下问题:
问题①—两个复数的积是什么数?它的值唯一确定吗?
生:通过观察,我们发现,两个复数的积仍是复数,它的值唯一确定。
师:问题②—当z1,z2都是实数时,与实数乘法法则一致吗?
生:根据法则,我们发现,当b=d=0时,z1,z2都是实数,复数的乘法与实数乘法法则一致。
师:问题③—复数的乘法类似于实数的哪种运算方法?
生:两个复数相乘,类似于两个多项式相乘,只要在所得结果中把i2换成-1,并把实部与虚部分别合并即可。
师:通过以上探究,我们知道,两个复数的积仍然是一个复数,且唯一确定,运算中与实数的乘法法则保持一致,类似于两个多项式相乘。
设计意图:与实数多项式的乘法进行类比,有利于学生理解复数的乘法法则,同时培养学生类比的核心素养。
(2)复数乘法的运算律
师:复数的加法满足实数运算中的运算律,那么,复数的乘法是否满足实数乘法的运算律呢?
教师和学生一起来验证乘法交换律,余下的以作业形式让学生自己来验证。
设计意图:引导学生根据复数的加法满足实数加法的运算律,大胆尝试推导复数乘法的运算律。培养学生的学习兴趣和勇于探索的精神。
(3)复数的除法法则
师:与复数减法法则的推导方法类似,我们利用复数的减法是复数加法的逆运算,利用复数的加法法则,推导出了复数的减法法则。现在,我们依据复数的除法是乘法的逆运算,利用复数的乘法法则,去推导复数的除法法则。即把满足(c+di)(x+yi)=a+bi,(a,b,c,d∈R)的复数x+y i,叫做复数a+b i除以c+di的商。
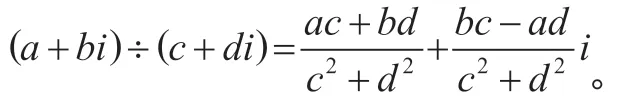
教师说明:在进行复数的除法运算时,通常先把相除的形式改写成分数的形式,再把分子与分母都乘分母的共轭复数,这里分子分母都乘分母的“实数化因式”(共轭复数),从而使分母“实数化”。
设计意图:通过将复数的除法转化成分式的除法,再类比实数中的分母有理化,对分母进行实数化,通过该化简的过程,帮助学生理解复数的除法法则。渗透类比和转化的数学思想方法,体会数学知识的紧密联系。
(4)例题讲解
①复数的乘法对应例题。
例:计算(1-2i)(3+4i)(-2+i)。
教师分析:复数的乘法,类似于多项式乘法,从左到右进行计算。注意,在结果中如果遇到i2换成-1完成计算。
例:计算(1)(2+3i)(2-3i);(2)(1+i)2。
教师分析:可以利用复数的乘法法则计算,也可以用与实数系相对应的乘法公式计算。
设计意图:及时运用新的理论知识,进行应用和巩固练习,让学生体验成功。使学生实现从掌握知识到运用知识的转化。在计算的过程中,锻炼学生的计算能力,培养学生数学运算的核心能力。
②复数的除法对应例题。
例:计算(1+2i)÷(3-4i)。
教师分析:先将除法化成分式的形式,再进行分母实数化运算。
③提升练习。
在复数范围内解方程x2+2=0。
设计意图:在熟练应用复数的乘法除法运算法则之余,进行提升练习。让学生先独立思考,提高学生的建构能力及主动发现问题、探究问题的能力。分层教学,让不同能力水平的学生学有所得。
在复数范围内解方程ax2+bx+c=0。
通过计算观察发现两个根互为共轭复数。
设计意图:让学生探究讨论在复数范围内如何求解方程,同时也让学生学会举一反三。
④开展“我是小老师”活动。
以小组为单位组内出题,做出准确答案,然后做其他小组出的题。
设计意图:突破学生的固定思维模式,从“我是出题人”的角度出发,思考怎样把复数这部分知识学得更扎实、牢固,然后再能力提升,学以致用。
3.课堂总结
①复数代数形式的乘法法则:两个复数相乘,类似于两个多项式相乘,只要在所得结果中把i2换成-1,并且把实部与虚部分别合并即可。
②复数代数形式的除法法则。
③在进行复数的除法运算时,通常先把相除的形式改写成分式的形式,再把分子与分母都乘分母的共轭复数,将分母“实数化”。
设计意图:通过课堂小结,增强学生对复数代数形式的乘法除法运算的理解,引导学生自我反馈、自我总结,并对所学知识进行提炼升华。
●教学反思
在新课程背景下,如何有效利用课堂教学时间,尽可能地提高学生的学习兴趣是一个重要的课题。教师首先要对新课标和新教材有整体的把握和认识,才能将知识系统化,注意知识前后的联系,形成知识框架、知识网络。笔者首先了解了学生现阶段的认知水平和年龄特点,因材施教,并围绕复数的乘除运算逐步展开。课上,笔者选择的题目呈阶梯式展现,且紧密联系新课改新高考,与时俱进。同时,“我是小老师”这一环节培养了学生的创造性,提高了学生学习的主动性。
本课虽然完成了教学设计中的各个环节,学生的能力也得到了相应的提高,但仍有不足,如:教学设计中的例题比较多,课堂上的时间比较紧张;课后没有做很好的小结。如果在教学设计和课堂中处理好这些问题,这节课也许会更好。
因此,在以后的教学中笔者还要经常反思,不断提高自己的教学水平。
