指向深度学习的“排列组合”高三复习教学探究
2023-03-15吴景峰

[摘 要] 针对高三复习过于功利而存在的浅表、低效学习现象,以“排列组合(第1课时)”高三一轮复习教学为例,阐述如何在高三复习课中,贯彻单元整合理念,创设层层递进的问题情境,落实对话指导与反思指导,促进深度学习.
[关键词] 深度学习;高三复习;排列组合
基金项目:广州市教育科学规划2021年度青年专项课题“‘O2O教学模式在艺术生数学教学中的实践研究”(202113695),广州市教育科学规划2022年度名师专项课题“基于深度学习的高中数学主题教学研究”(202214227).
作者简介:吴景峰(1986—),中学一级教师,广州市高中数学十佳青年教师,广州市特约教研员,广州市骨干班主任,广州市施永红名教师工作室成员,广东省钟进均名教师工作室成员.
引言
新高考背景下,迫切需要提升学生的数学核心素养,对数学教师的高三复习也提出了更高要求. 《普通高中数学课程标准(2017年版2020年修订)》(以下简称《标准》)指出,教学中要关注育人目的,注重培养学生核心素养,提高學生综合运用知识解决实际问题的能力,帮助学生把握学习的深度[1].
深度学习为此提供了重要途径,它是“学习者能动地参与教学的总称”[2]. 它从问题的揭示开始,学生围绕问题思考,寻求种种解决方法,教师则纵观全局,判断学生的最近发展区,指引学生展开以解决问题为目的的探究活动[2]. 它有三个重要特征:一是强调学生立场,关注教师指导下学生的有意义学习;二是强调单元整体教学,强调学习的挑战性,强调学科基本知识、基本方法、基本思想的学习和理解;三是强调教学的育人功能,落实到学生素养的发展上,落实立德树人[3].
“排列组合”高三复习课教学现状
当前高三复习教学普遍存在浅表、虚假、低效的学习现象和行为,根源在于问题设计失效、情境创设失真、师生互动失衡,难以激发并维持学生有效的思维活动,影响了学习质量和效果[4]. 在“排列组合”高三一轮复习中主要表现为:①教学问题的设计缺乏系统性、层次性和关联性. 部分教师分类讲解排列组合的题型,例如先讲排列的题型,再讲组合的题型,这样复习既割裂了整个知识体系,也容易忽略各类问题的关系. ②情境创设缺乏时代性、真实性和挑战性. 复习时,很多问题情境是陈年已久的例子,难以激发学生的兴趣和思维主观能动性,思维层阶偏低. ③师生互动缺乏针对性、目的性和实效性. 授课时,部分教师为赶复习进度,对排列组合问题难点的处理,通常以全班口答的形式进行,造成“学生都懂”的假象,没有充分暴露学生的思维. ④对思维激发的引导不够,探究浅尝辄止,概括浮于表面. 解决排列组合问题需要的思维量很大,教师的引导很多时候代替了学生的思考,导致学生的思维结果“含金量低”[4].
针对需求与现状的差距,很多学者以深度学习为理论依据开展各种高三复习教学的研讨活动,本文以笔者某次异地实践教学探究为例展开论述.
“排列组合”复习课案例描述
笔者在某次异地教学活动中,以“排列组合(第1课时)”为课题上了一节高三复习示范课. 课前,笔者通过线上问卷形式布置了课前任务,要求每位学生从身边寻找一个关于排列组合的数学问题,然后自主编题并解答,意在考查学生是否已了解排列组合的含义. 笔者在课前把学生编制的题目进行了整理,分成了两类,一类是经典错例,另一类是答案正确的题目. 第一类题目用于课前3分钟展示,师生共同纠正;第二类题目作为题库随机选取,作为课前3分钟的课堂引入.
课堂上,笔者随机选取了两道学生编制的题目(问题1、问题2)作为课堂引入:
问题1:有3张相同的参观券,要在5人中确定3人去参观,不同的方法有多少种?
问题2:要从5件不同的礼物中选出3件分别送给3位同学,不同的方法有多少种?
追问1:问题1与问题2的本质区别是什么?
追问2:问题1与问题2的联系是什么?
变式1:有m张相同的参观券,要在n人中确定m人去参观,不同的方法有多少种?
变式2:要从n件不同的礼物中选出m件分别送给m位同学,不同的方法有多少种?
师生活动:随机挑选个别学生回答,并表扬编题者.
设计意图 让学生自主编题,明确复习内容,并通过追问,让学生回忆排列组合知识,重视知识间的联系.
问题3:某中学的模特队中有5名男生,3名女生,按以下要求排成一排拍照,分别有几种方法?
(1)女生必须相邻;
(2)女生都不相邻;
(3)女生甲排在女生乙的左边;
(4)女生甲不能排在最左,也不能排在最右.
追问3:若第(3)问中的甲、乙两人,由两个完全相同的女模特道具代替放进队伍中,方法数是否变化?与原问题的区别是什么?
师生活动:学生独立思考,限时训练5分钟,5分钟后开展3分钟的小组讨论,学生上台“说数学”进行交流.
设计意图 利用异地教学所在学校的情境,一以贯之创设5个题目,转化为8个元素限制条件下的排列组合问题,以此整合零散的方法便于学生发现问题间的联系与区别.
变式3:如图1所示,这是某中学校园内的三个篮球场,甲同学在A点处,想用最短路径去B点处拿回自己的水杯,但由于每个半场内均有其他同学在打篮球,于是甲同学只能沿着如图2所示的黑色路径行走. 问:甲同学的行走路径有多少条?
师生活动:学生展开讨论,全程参与,共同探究,笔者选择个别学生提问.
设计意图 利用异地教学所在学校的校园地图创设变式3,让学生先从一条条路径数,到思考如何列举,再发现前后问题的相通之处,强调排列组合问题表征,增强学生的分析能力,同时体会转化与化归思想的美妙,实现最近发展区的进阶.
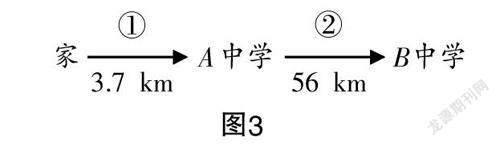
问题4:今天早上W老师从家出发,先到达A中学,中午再从A中学出发,到达B中学给同学们上课,线路如图3所示.
图3
第①段线路可供选择的出行方法:步行、自行车、出租车、私家车、公共交通工具.
第②段线路可供选择的出行方法:步行、自行车、出租车、私家车、公共交通工具.
问:按上述线路,W老师共有多少种出行方法?
师生活动:全班齐声回答“25种”,笔者反问条件是否充分,全班学生恍然大悟,笔者继续补充以下几点.
(1)公共交通工具有公交车和地铁;
(2)私家车从家出发;
(3)考虑路途用时不宜过长,因此步行不超过5 km,自行车骑行不超过10 km.
追问4:按上述线路,W老师共有多少种出行方法?
师生活动:落入“陷阱”后,学生积极展开讨论,笔者选择个别学生提问.
设计意图 利用W老师的出行经历来设计多限制条件的排列组合问题,先让学生落入“陷阱”,思维受阻,再启发学生抓住关键的限制条件进行有序思考,提升其分析问题的能力.
变式4:某中学模特队的5名男生排成一排拍照,其中男生X不能排在最左,男生Y不能排在最右,有几种排法?
变式5:某中学模特队有5名男生,3名女生,从中选出3名学生作为代表,且至少有2名男生,共多少种方法?
师生活动:限时训练,学生完成后核对答案,师生共讨.
設计意图 通过变式训练,引导学生从本质上理解排列组合是枚举法的一种转化,遇到多限制条件的计数问题时,要学会抓核心条件转化问题,展开分类枚举,通过分类简化问题.
问题5:某人想邀请朋友来家中聚会,写好了4封请柬,需要装入4个信封,结果因为粗心把请柬全部装错了信封. 请问:装错的可能情况有多少种呢?
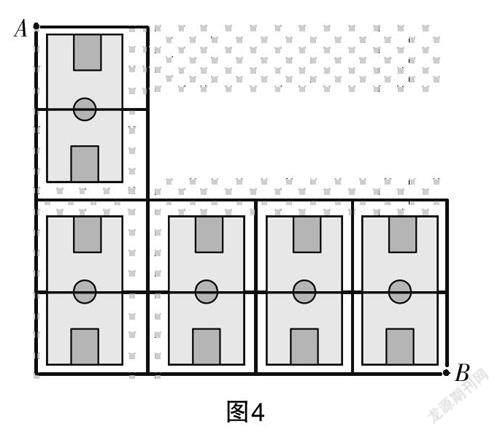
问题6:某中学校园内共有5个篮球场,甲同学在A点处,想用最短路径去B点处,但由于每个半场内均有其他同学在打篮球,于是甲同学只能沿着如图4所示的黑色路径行走. 问:甲的行走路径有多少条?
设计意图 问题5改编自著名的伯努利—欧拉装错信封问题,是数学史上著名的数论问题,也是排列组合问题——通过历史名题渗透数学文化;问题6改编自变式3,是留给学生的挑战任务.
最后,笔者提出了两个问题:①本节课解决了哪些类型的问题,其区别与联系是什么?②学习本课后,对编题有何感受?能否利用其他同学或老师编制的题目,进行二次改编?引导学生学后反思,教师布置分层作业——大部分作业来自学生线上自主编制的题目.
指向深度学习的排列组合高三复习教学的启示
深度学习是以学生为主体的,只有通过学生积极主动地全身心参与才能实现[3]. 因此,在高三第一轮复习中,要提高学生参与的自主性和深度,将学生内在学习动机的激发和维持及思维的参与贯穿教学始终,这是高三数学有效复习所需要的[5].
1. 单元整合,聚焦生成
排列组合的综合应用是高考的重难点,问题情境常考常新[6],因此在高三的复习课中,“单元整合”理念要贯穿教学始终.
首先,从教师“教”的创造加工视角来看,单元设计是出发点. 为避免学生在运用排列组合模型的过程中,因缺乏深度理解而张冠李戴[6],案例中的问题3与变式3,把相邻问题、不相邻问题、定序问题、相同元素问题等整合为单一条件限制问题,并归纳出特殊元素(位置)的特殊处理方法;问题4、问题5、问题6以及变式4、变式5则是多限制条件计数问题的整合,引导学生归纳核心方法,实现“多题归一”.
其次,从学生“学”的生成过程视角来看,聚焦生成是落脚处. 《标准》指出,高考考查内容应围绕数学内容主线,聚焦学生对数学知识的理解和应用[1]. 案例中,笔者在课前线上组织学生自主编题,并随机抽取题目作为课堂引入,既有反例又有正例,促进学生回顾知识,调动学生积极性,是异地教学中线上线下融合的一次尝试. 问题3让学生上台“说数学”,暴露学生的思维;变式3先让学生尝试解答,再集思广益寻求更优方法;问题4设计了“小陷阱”,引发学生认知冲突,从而让学生意识到问题分析的重要性,体现“练在讲之前,讲在关键处”[7].
这需要在单元设计中预设,在课堂实施中生成,寻求两者的平衡点,让高三复习充满智慧与活力.
2. 情境创设,分层启诱
《标准》指出,在教学活动中,教师应结合教学任务及蕴含的数学学科核心素养设计合适的问题情境,引导学生用数学的眼光观察现象发现问题,用恰当的数学语言描述问题,用数学的思想方法解决问题[1]. 案例中,笔者通过创设三个问题情境组由浅入深地对学生进行分层启发诱导. 第一个情境组,放手让学生去发现与创造问题,通过学生线上编题,达到学生再认识排列组合的目的,除了概括排列组合外,还要从自己的视角出发观察身边的例子,得出自己对所学内容的理解,为进一步学习做好铺垫. 第二个情境组是问题3与变式3,笔者利用学生熟悉的校园情境创设问题,把学生所在校园的地图截取在变式3中,大大调动了学生学习的参与度,同时把零散的问题类型与解决方法串联起来,诱导学生发现各类问题的联系与区别. 第三个情境组是问题4,从笔者的实际情境出发进行创设,先让学生感觉很容易,继而发现问题不简单,认知冲突后再启发学生有序思考. 另外,还有以数学史为背景的问题5,渗透着数学文化.
3. 对话指导,加强交流
相互对话的教学即“对话指导”,是深度学习的重要支撑. 它包含三种对话——与自己的对话、与他者的对话、与客体的对话[3]. 案例中,笔者先在课前组织学生自主编题,师生共同纠正经典错例,构建师生“畅所欲言”的课堂生态;然后以现实生活为背景创设情境问题,营造“用数学的眼光观察世界”的课堂气氛;再在课中组织学生小组讨论,让学生“说数学”,充分暴露学生的思维,让学生感受到笔者对他们“犯错”与“不理解”的宽容;又利用问题4的“小陷阱”,让全班学生感受到“共同犯错”的愉悦,加以启诱,感觉到“发现”的惊喜,充分调动学生对话与情感投入;最后通过布置挑战性任务,整理学生编制的题目来布置作业,加强学生课后的数学交流. 通过三种对话及相互作用,促进深度学习.
4. 反思指导,提升素养
在每个教学环境的最后阶段,给学生适当的留白空间进行反思十分重要,能使学生感受到充实感,即“达成感”与“自我有能感”. 例如解决问题3时,学生上台板演后,笔者让学生“说数学”——除了说解题过程,更重要的是引导学生说“反思”与“总结”. 解决变式3时,笔者让学生通过讨论及时反思,总结问题模型的共性方法,让学生能够确实感受到“会做了”. 布置作业时,利用学生自编的题目让学生感受到“别人改编的题目,我也能做”,让编题的学生感受到“我也能做小老师”. 在这种元认知的反思下,学生才能真正体验到深度学习,提升自身素养,这对学生的可持续发展有重要意义.
参考文献:
[1] 中华人民共和国教育部.普通高中数学课程标准(2017年版2020年修订)[M]. 北京:人民教育出版社,2020.
[2] 钟启泉. 深度学习:课堂转型的标识[J]. 全球教育展望,2021,50(01):14-33.
[3] 刘月霞. 深度学习走向核心素养[M]. 北京:教育科学出版社,2019.
[4] 戴建仁,李志洪. 创设数学问题情境〓促进学生深度学习——以《计数原理的综合应用》为例[J]. 福建中学数学,2020(11):18-21.
[5] 伍春兰.检视高考数学第一轮复习——以排列组合复习为例[J]. 数学通报,2017,56(12):37-38.
[6] 韦崇裕. 基于深度学习的“排列与组合”微设计[J]. 中学数学教学参考,2021(04):65-67.
[7] 周伟锋. 练在讲之前,讲在关键处——有效提高数学课堂教学效率的途径[J]. 中学数学研究(华南师范大学版),2006(04):9-11.
