基于GNSS-A的海洋声速变化估计及其对定位的影响
2023-03-15张盛秋杨元喜徐天河
张盛秋, 杨元喜, 徐天河
1 长安大学地质工程与测绘学院, 西安 710054 2 地理信息工程国家重点实验室,西安测绘研究所, 西安 710054 3 山东大学(威海)空间科学研究院, 山东威海 264209
0 引言
海洋定位、导航和授时(Positioning, Navigation and Timing, PNT)依赖于精准的水下时间测量,由于海水对电磁波能量具有较强的吸收作用,Spiess(1980)提出的全球卫星导航系统/声学测距组合技术GNSS-A(Global Navigation Satellite System-Acoustic ranging combined)得到了广泛的应用(Sato et al., 2013; Chen et al., 2019; Sakic et al., 2020; Yang et al., 2020; Yang and Qin,2021),与之相关的硬件设备与软件算法也在不断发展(Ishikawa et al., 2020; Watanabe et al., 2020). GNSS-A的观测系统由海面单元(通常为船只或浮标)和海底应答器组成. 海面单元包含GNSS天线、船只姿态传感器和船底换能器,因此可以在国际地球参考框架(International Terrestrial Reference Frame, ITRF)下利用动态GNSS实时确定海面单元的位置. 海底转发器接收换能器发射的声学信号后将信号发送回换能器,利用M序列码的特性,通过识别往返信号相关图中最高峰获得时延.
GNSS-A系统的海面误差源主要来源于动态GNSS本身的误差源以及姿态传感器的测量误差,水下误差源主要包括声速误差、时间偏差和海底应答器的硬件延迟. 其中最为重要的是声速时空变化导致的误差,其高频部分在时间平均后不会产生较大的影响,但是低频部分对于海底定位来说不容忽视.
我们知道,海洋声速存在时空变化,声速沿声线路径的变化将直接影响声波测距,因此声学测距中必须考虑海洋中随潮汐周期以及气象因素变化的洋流(Spiess,1985). 声速的时间变化包括年变化、季节性变化、由温度引起的日变化和内波引起的短周期变化. 当假设声速为水平分层时,则需要考虑声速的水平不均匀性,这种空间变化可能由内波、洋流驱动的异常海水平流或其他因素造成(Honsho et al., 2019). 声速的时空变化严重影响着海底应答器定位的精确度,在单点定位模式的声学测量误差数值模拟实验中,声速变化对应答器的位置影响可达18 cm(Yamada et al., 2002). 对于应答器阵列,声速的水平空间变化可能导致阵列位置几个厘米的偏移(Kido,2007).
不同海域声速是变化的,相同海域不同时间声速也是变化的,而且这些变化几乎不可预知,即便进行频繁的声速测量也无法保证声速时空的连续性. 在2.5~4.5 km水深下,3 h的CTD(Conductance, Temperature and Depth)观测不可能完全跟踪声速时间变化(Osada et al., 2003). 声速剖面是构建声速模型的重要手段. 然而,声速剖面是海水温度、盐度和静水压力的函数,不同经验公式计算的声速差异很大,且随深度线性增加,2000 m可达0.55 m·s-1,双向延迟达0.3 ms(Kido et al., 2008),此外还存在设备的固有误差. 因此,通过现场测量来实时获取海洋中随时间和空间变化的声速很难做到(Fujita et al., 2006; Kido et al., 2008).
针对声速的时空变化,可以采用一些特殊观测方法来削弱其影响. Spiess等(1998)将固定海面单元置于三个或四个海底转发器的水平中心位置进行海底地壳监测(Scripps Institution of Oceanography, SIO方法),得到水平精度优于4 cm的海底基准点坐标. 随后多位学者都使用了类似观测方式(Osada et al., 2003; Kido et al., 2006, 2008; Tomita et al., 2015, 2017),这种方法是建立在声速仅随深度变化的假设条件下的. 由于测量时间一致性与几何对称性,将显著削弱阵列中心的声速变化,这意味着SIO方法能够精确测定阵列中心的水平位置. 但是声速变化对阵列中心位置的垂直分量影响仍然没有消除,同时如果声速存在空间变化,SIO方法阵列中心的水平精度将会出现恶化. Asada和Yabuki(2001)尝试了走航观测,得到大约4 cm的水平定位精度. 后续多位学者采用对称设计的走航测量(Yokota et al., 2019; Kinugasa et al., 2020; 马越原等, 2021b; Yang and Qin,2021; Zeng et al., 2021),对称构型在一定程度上能够削弱呈周期性变化的系统误差,其原理与SIO方法具有类似之处.实际上,海面观测无论采用何种构型,由于不具有时间一致性,声速的时间变化和空间变化将会耦合影响海底定位.此外,船体姿态数据噪声的影响也不可忽略.Xu等(2005)给出了系统误差近似公式,并提出了海底单点定位的单差法与海底相对定位的双差法.其中双差法基本只受随机误差的影响,且不要求对称观测,可实现海底基线向量亚厘米级测量精度.
声速变化对于某一历元往返时间的影响可由标量声速描述,这表明相对于某一特定声速结构的声速扰动可以与应答器位置同时求解.Obana等(2000)仅用一个声速剖面得到的往返观测残差发现一些系统趋势,这种声速结构之间的差异提示我们,同时确定海底参考位置与声速结构是十分必要的.Fujita等(2006)和Ikuta等(2008)在声速求解上做出了系统性成果,前者采用不同时间窗口的二次多项式估计平均声速的时间变化,大大提高了定位精度.后者采用B样条拟合声速的连续变化,通过同时求解声速结构和基准位置得到厘米级的定位结果.声速的空间梯度被证明可以使用水平距离的线性函数建模(Kido,2007),这种方法提取的声速变化与声速测量结果具有一致性(Kido et al., 2008).随后多位学者在观测方程中构建了声速的时空变化模型(Yasuda et al., 2017; Yokota et al., 2019; Kinugasa et al., 2020; Watanabe et al., 2020),同时声速的空间梯度场有可能反映海洋的水平结构(Yokota and Ishikawa,2019).
本文重新推导了时间延迟函数模型,给出了更为严谨的时间延迟-声速扰动关系式和参考声速的求解方程.基于B样条曲线和贝叶斯估计提出了一种声速扰动建模方法与参数估计策略,并将该算法应用于我国深海实测声学数据,得到了海底定位结果和声速变化特性.
1 水下声线跟踪方程
1.1 基本方程推导
如图1所示,双程声线跟踪模型是水下声学定位的基础.如若不考虑声速的时空变化,在观测历元i,声线跟踪观测方程可以表示为:
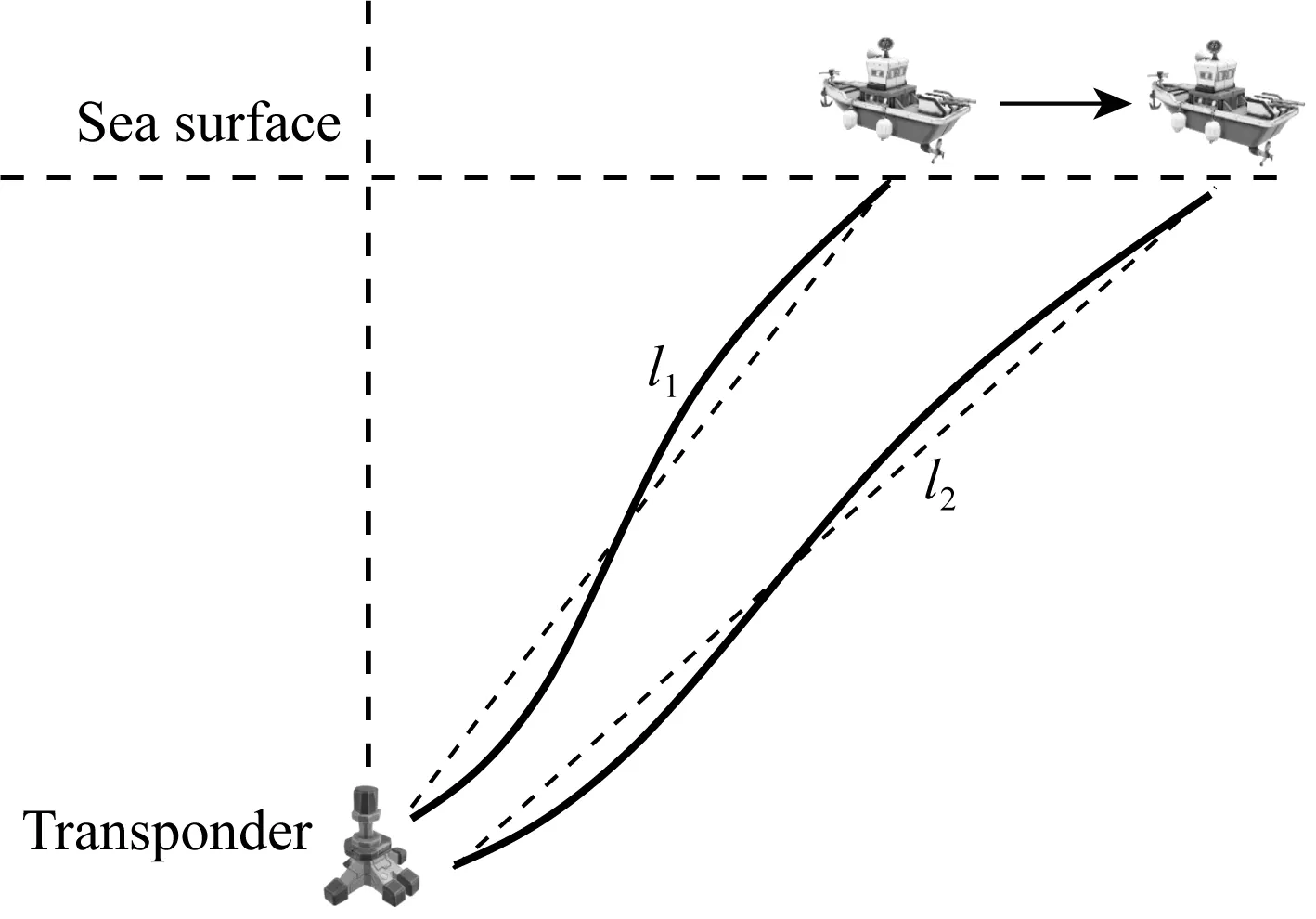
图1 双程声线跟踪模型Fig.1 Acoustic ray tracking model of round trip
Ti=T(x1,y,V(u))+T(x2,y,V(u))+εi,
(1)
式中x1表示信号发射时刻船底换能器矢量,x2表示信号接收时刻船底换能器矢量,y为海底应答器的坐标.V(u)表示已知水平分层的声速剖面,T(*)为遵循Snell反射定律的声线跟踪函数过程,Ti为往返测量时间,εi为测量偶然误差.至少3个方程即可利用最小二乘求解海底应答器的坐标,此时由于声速的时空变化,方程(1)中会存在一定的系统误差.
可以根据沿着声线路径的积分时间建立严格的声速扰动方程:
(2)

(3)
ln(T(x1,y,V(u))+T(x2,y,V(u)))-ln(Ti)
(4)
由此得到包含声速扰动的声线跟踪观测方程,如果认为任意时刻声速扰动相同,则可得到:
ln(T(x1,y,V(u))+T(x2,y,V(u)))-ln(Ti)
(5)
方程(4)(5)为求解声速问题的两个极端情况.对于方程(4),每个历元将包含两个声速扰动参数,如若不加入约束条件则方程欠定.而方程(5)强制所有声速扰动不变,此时至少4个方程便可使用最小二乘求解,但是固定不变的声速参数无法反映声速的波动性质.因此需要使用合理的约束条件对声速扰动建模,方程(5)可以用于求解较为精确的坐标初值.
需要指出,引入声速扰动参数一个不可避免的问题是其与海底应答器垂向坐标参数强相关,这意味着利用方程(5)解算某些入射角变化幅度不大的数据时(例如圆走航),可能会出现病态问题.此时可以利用已知的声速结构通过方程(1)计算,这种情况下声速误差将直接影响垂向坐标准确度.
1.2 参考声速的求解


图2 等梯度声线跟踪算法Fig.2 Constant-gradient acoustic ray tracking method

(6)
(7)
(8)
其中θ0为声线入射角,p为Snell常数,Rk为声线在该层的圆弧路径半径.由此可以得到声线在此深度区间的水平距:
Δdk=Rk|cosθk-cosθk+1|.
(9)
声线入射角θ0和Snell常数p是需要迭代求解的.声线在所有深度区间的水平距之和等于船底换能器和海底应答器之间的水平距离,即:
(10)

(11)
(12)
(13)
式中S为声线传播总路程,T为声线传播总时间.
1.3 B样条曲线建模
针对声速扰动项ΔV,可以根据Weierstrass逼近定理采用多项式逼近.较为合理的假设是声速扰动在连续观测时间段内是光滑连续的,而B样条曲线作为分段多项式基函数的线性组合可以保证曲线的连续性,故可将声速扰动建模为时间的B样条函数ΔV(t)(Ikuta et al., 2008; Honsho and Kido,2017; Yasuda et al., 2017; Kinugasa et al., 2020; Watanabe et al., 2020).此时在第i个历元的观测方程(4)中有:ΔV1=ΔV(ti1),ΔV2=ΔV(ti2).ti1为该历元船底换能器发射信号时刻,ti2为船底换能器接收信号时刻.
考虑到声速的空间变化,将声速扰动分解为三个分量(时间变化与二维空间变化),分别采用定义在n+1个节点上的三次B样条曲线建模:
(14)
式中a1i、a2i和a3i为控制曲线的顶点参数,其中a1i为声速扰动的时间变化参数( m·s-1),a2i和a3i为声速扰动的水平梯度参数(m·s-1·km-1).d′为当前历元声线到达一定水深所走过的水平位移,φ为当前历元船底换能器相对海底应答器的方位角.Bi,3为三次B样条基函数,可以采用de Boor-Cox递推公式(Piegl and Tiller,1995) 得到三次B样条曲线的分段多项式基函数.如图3所示,第i个B样条基函数仅在[ti,ti+4)5个节点之间有定义:

图3 第i个3次B样条基函数的定义区间Fig.3 The interval defined for the ith cubic B-spline basis function
(15)
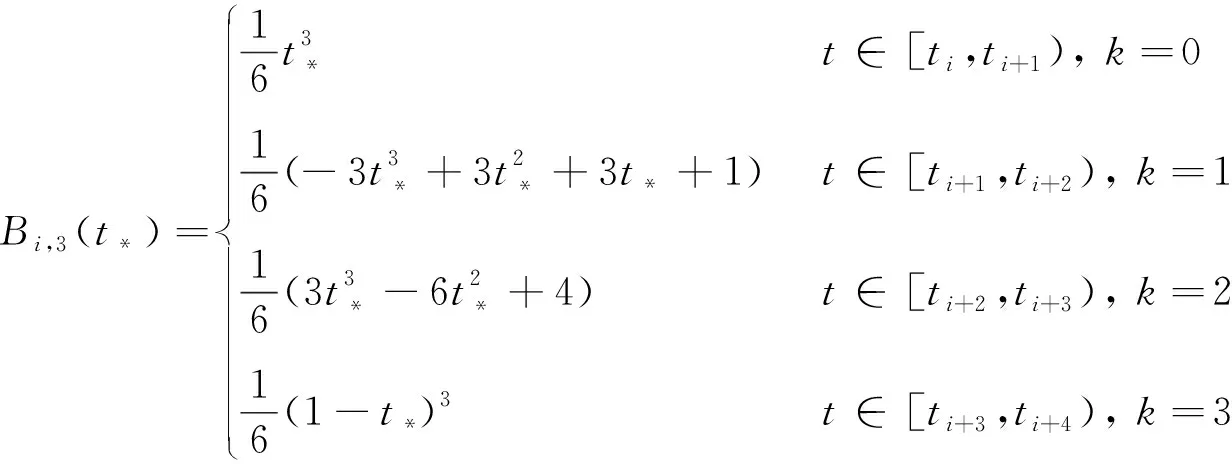
(16)
2 参数估计
求解公式(4)中的三维坐标和声速扰动两类参数,最简单的方式是固定一类参数去求解另一类参数,此时无法保证参数的无偏性.考虑采用贝叶斯估计对参数进行先验信息约束,三维坐标参数初值可以由公式(5)得到,对此非线性优化问题采用下降梯度求解局部最优即可.
2.1 先验信息控制与超参数选取
考虑先验信息的海底基准点坐标解算已经有学者做过探讨(马越原等, 2021a).我们这里的先验信息包括三维坐标参数初值、方差和声速扰动参数初值、曲线粗糙度.
若有m观测历元,整个观测时段设置为n+1时间节点,则共有3n+12个待定参数(包括3个坐标参数和3(n+3)个声速参数).采用二阶平滑来控制声速结构的光滑程度(Fessler,1991; Honsho and Kido,2017; Watanabe et al., 2020),并通过超参数调整.一般情况下声速的水平空间变化要小于声速的时间变化,因此控制空间梯度的变化更加平滑.此时对于参数初值与先验权阵可采用如下形式:
(17)
(18)
(19)
其中X0包含三维坐标初值和声速扰动参数初值,声速扰动初值设置为0.Bi,3(t)和Bj,3(t)均为B样条基函数(i,j=0,1,…,n+2).P0为所有参数的先验权矩阵.公式(19)包含DE0,N0,U0和μ两类超参数,其中μ控制着声速扰动曲线的光滑度,DE0,N0,U0为坐标初值方差.
超参数μ的选取将影响声速估计结果,我们希望在贝叶斯估计前选取最优的超参数,即确定声速的波动程度(曲线粗糙度).因为利用方程(5)求解坐标初值后的残差中保留了声速的波动信息,同时声速模型中包含强相关量,因此可以引入最小范数条件来选取最优超参数:
Pa=diag(Pi,j102Pi,j102Pi,j),
(20)
(21)
(22)
其中Pa为声速参数的先验权矩阵,ρ为方程(5)最小二乘更新后的残差序列,B为函数f′对所有声速参数的雅可比矩阵,则满足:
a=(BTB+μPa)-1(BTρ),
(23)

(24)
公式(23)(24)表明,通过选取合理的μ值使得声速参数向量的二范数最小.
对于坐标参数先验方差DE0,N0,U0,如果取值较小,意味着坐标初值具有较强约束作用,声速扰动反演类似于Yang和Qin(2021)直接使用残差建立时域上的系统误差模型.如果取值较大,先验约束较弱,定位结果收敛后可能会出现一定程度的偏移,尤其是方程出现病态情形.
2.2 贝叶斯估计与精度评定
对于先验信息与待估参数有:
(25)
观测方程(4)可以化为:

(26)
f=ln(T(x1,y,V(u))+T(x2,y,V(u)))
(27)
(28)
A为所有参数的雅可比矩阵.构造目标函数:
(29)

(30)
参数的验后协方差矩阵为:
(31)
(32)

3 数据计算与分析
3.1 数据与算法步骤
2019年7月14日至16日对1个海底应答器进行了3000 m水深声学定位实验,该应答器采用方舱固定.实验采用三种观测构型,图4显示了海底应答器与观测数据的水平空间关系,其中黄线对应数据Data 1;红线对应数据Data 2;蓝线对应数据Data 3.表1给出了三种数据的详细信息,可以看出它们为不同时间段的观测,不同数据的计算结果可以相互检验.Data 3不是连续的数据,不同时间段之间相隔3或4 h,而方程(4)的前提假设是只有连续的数据具有连续的声速扰动,所以对Data 3采用3条独立的B样条曲线建模.此时不同时间跨度的声速扰动将无关联,但是仍然共同影响着海底应答器坐标的确定.理论上,在连续时间段内取越多的B样条时间节点,建模效果会越好,但也有可能会出现过度参数化问题.本文以30 min为间隔取时间节点,时间节点数目与观测时间长度成正比.

图4 观测数据的时空关系Fig.4 Space-time relationship of observations

表1 观测数据信息Table 1 The information of observation
图5显示了试验期间所测量的4个声速剖面,表2给出了声速剖面测量的具体信息.从图5可以看出0~1800 m深度下4个声速剖面具有一定差异,同一水深最大声速差异为1.43 m·s-1,这证明了声速确实是存在时空变化的.因为声速的时空变化一般存在于水层的较浅部分(Kido et al., 2008; Yasuda et al., 2017),所以本文只利用声线到达水深1800 m时的水平位移来求解声速的水平空间梯度.从表2可以看出声速剖面的测量是十分耗时的.

表2 声速剖面测量信息Table 2 Detailed information about SVP
在这长达2~3 h的测量过程中,声速结构很有可能已经发生了变化.4个声速剖面中只有1个声速测量的最大水深超过3100 m,但是由于深海中声速基本随深度线性变化,可以通过最小二乘外推获得直至海底应答器深度的所有声速值.
数据处理过程如下:
(1) 通过包含固定声速扰动参数的观测方程(5)获得应答器坐标初值(E0N0U0)和模型残差ρ(在圆走航数据处理中,可以选择使用方程(1)).
(2) 基于约束最小二乘公式(23)—(24),利用步骤(1)得到的残差来估计与声速扰动参数相关的最优超参数μ.
(3) 基于包含3次B样条声速扰动参数的声线跟踪方程(4),迭代求解应答器坐标和声速的时间变化与空间梯度,直至海底点三维坐标改正数小于0.1 cm.
(4) 将求得的声速扰动看作已知量计算海底点坐标精度.
因为深海观测环境复杂,步骤(1)采用3σ为粗差剔除标准.从公式(14)可以看出,定义在n+1个节点上的声速模型将包含3n+9个声速参数.因此对于整个算法来说,节点个数取得越多,模型参数越多,解算效率越低,建立的系统误差模型越复杂.定位精度取决于系统误差模型的平滑度,误差模型越平滑,定位精度越低.相反模型局部波动越大,定位精度越高,但此时模型可能不符合声速的实际变化规律.
3.2 海底站坐标与声速分析
图6给出了不同数据的超参数选择结果.表3和图7分别为海底点的定位结果和不同观测时段内声速的时间变化以及二维空间梯度变化.图8、图9和图10分别为参考声速值,整合后的声速扰动与所有历元实际声速标量值.

表3 定位结果与精度Table 3 Positioning results and precision
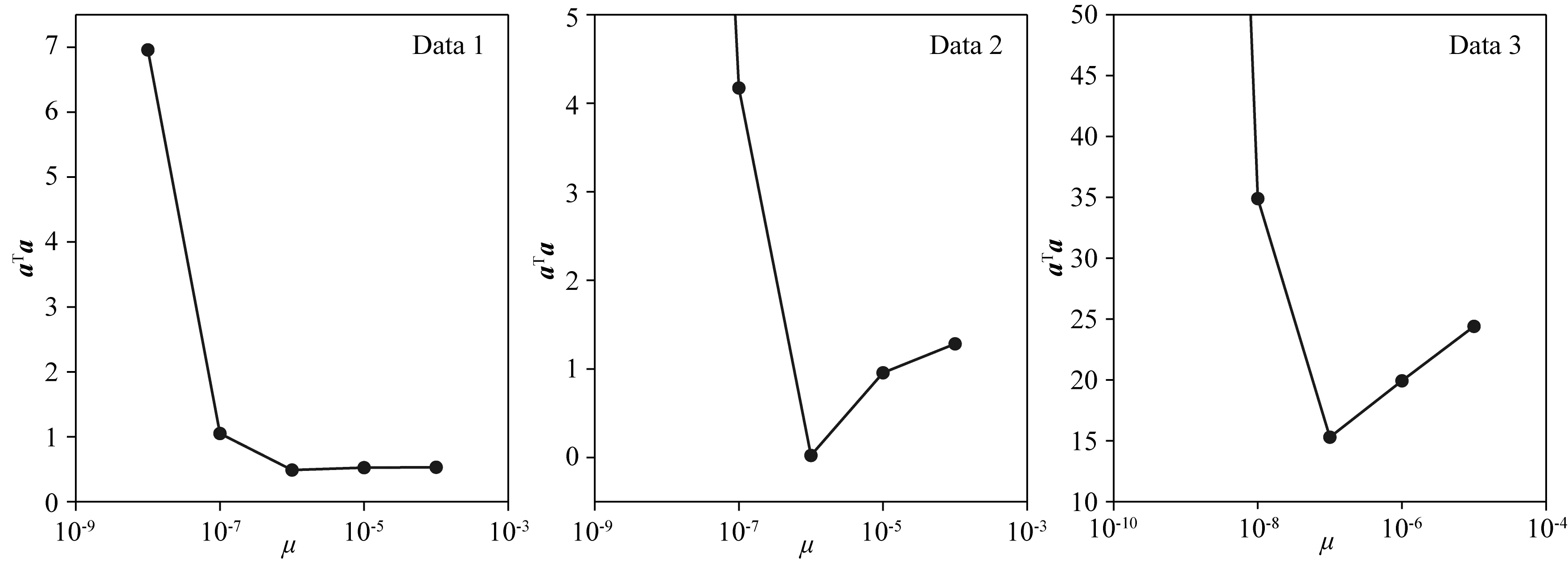
图6 Data 1, Data 2和Data 3的超参数选取Fig.6 Hyper-parameters selection of Data 1, Data 2 and Data 3

图7 不同数据的声速时间变化与二维空间梯度(a) Data 1; (b) Data 2; (c) Data 3.Fig.7 Temporal variation of sound velocity and two-dimensional spatial gradient of different data sets

图8 参考声速Fig.8 Reference sound velocity
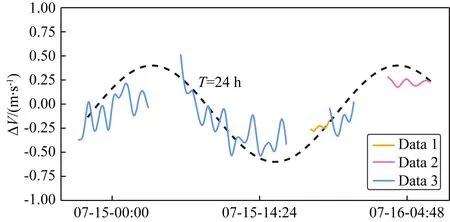
图9 总体声速扰动Fig.9 Total sound velocity perturbation

图10 总体声速变化Fig.10 Total variation of sound velocity
如图6所示,当μ=10-6时,Data 1和Data 2声速向量的二范数最小,而Data 3的最优超参数为10-7.考虑到Data 1和Data 2都为圆走航,其垂向坐标较易受到病态问题或声速误差的影响,故依次选取坐标先验方差为:
D1E0,N0,U0=diag(105105107),
D2E0,N0,U0=diag(105105108),
D3E0,N0,U0=diag(105105105).
表3给出了海底点三维坐标和方差均方根(内符合精度).从坐标差异的角度分析:不同数据集N坐标分量重复度最好,E坐标分量重复度最差.不同数据集之间E/N/U分量的最大差异分别为0.391,0.035和0.120 m.而Data 1和Data 2的E坐标分量非常接近,仅相差0.016 m,有理由推测是Data 3的声速结构差异导致其E坐标分量的偏移,本文在后续的声速结果中解释了这一现象.
从定位精度可以看出,所有数据解算的坐标精度均达cm级.其中Data 3的ENU三分量精度均为最优,这得益于其20 h的长时间观测.半径为1.5倍水深的Data 2具有较高的三维位置精度,且各分量精度近似,这与许多学者研究得到的结论是一致的(Zhao et al., 2016; Xue and Yang,2017; Chen et al., 2020).Data 2的垂直精度差于Data 1,这可能是声线入射角较大所致,较长距离的声学测距可能带来较大的测量误差,同时垂直精度衰减因子(VDOP)也将变差.
如图7所示,不同数据的声速扰动分量图包含3部分:黄线表示声速的时间变化,中间红蓝线表示声速的南北/东西空间梯度,下方红蓝线表示声速的空间变化,空间变化为空间梯度与相应水平距离的乘积.因为Data 1和Data 3部分时段声速空间变化较大且部分航迹非均匀变化,B样条局部调和特性可能造成局部空间梯度估计异常.故可对其适当加大约束:认为整个观测时段内空间梯度固定,这不仅减少了待估参数的数量使运算得到简化;同时更有利于空间梯度之间的相互比较.需要说明的是,这些声速扰动是建立在固定声速剖面SVP-1512上的,选取此声速剖面的原因是其与所有数据集的时间重合度最好.
可以看出Data 1声速的时间扰动在-0.27 m·s-1至-0.16 m·s-1之间,也即比参考声速更慢.Data 2声速的时间扰动在0.18 m·s-1至0.26 m·s-1之间,相比于参考声速更快.Data 3则分布较为均匀,大部分时间处于-0.5 m·s-1至0.5 m·s-1之间.图7a,c显示Data 1和Data 3的声速空间梯度均小于0.04 m·s-1·km-1,且都为南北方向梯度明显大于东西方向梯度,说明两者观测时段内声速的水平空间结构具有一定的相似性.同时Data 1声速的空间变化小于0.04 m·s-1,Data 3声速的空间变化小于0.1 m·s-1.图7b反映出Data 2两个方向的空间梯度变化范围较为一致,声速的空间变化小于0.03 m·s-1.
如图9所示,整个时间轴上声速扰动呈现类似于正弦函数的长周期日变化与内波导致的短周期波动,这表明了声速估计与实际情况的一致性.其中黄线对应Data 1、红线对应Data 2、蓝线对应Data 3.黑色虚线对应周期为24 h的正弦曲线.声速扰动整体处于-0.5 m·s-1至0.5 m·s-1之间,变化幅度小于1 m·s-1.图10显示了所有声线路径上的标量声速值变化,它是参考声速与声速扰动之和.可以看出声速值大致在1494.8 m·s-1至1495.8 m·s-1之间波动,变化幅度小于1 m·s-1.
声速的周期性时间变化远大于空间变化,同时船体不断移动,因此不同区域的声速平均值由于声速的时间变化而不同.由图10中Data 3所有历元声线的标量声速值,可展示出Data 3不同区域的平均声速.如果对Data 3所有航迹点进行南北分域和东西分域,并假设分域后所有观测点相对于应答器分布均匀,则可以计算出南北分域的平均声速差值为0.001 m·s-1,东西分域的平均声速差值为0.034 m·s-1(如表4所示);而且东西声速差异是南北声速差异的34倍,具体表现为东快西慢.

表4 不同区域的声速
图11展示了声速差异对定位结果的影响.对于所有关于应答器对称的观测数据对,应答器西侧声速都比东侧平均慢0.034 m·s-1.最小二乘估计的本质是平衡差异,坐标定位结果会附和声速的变化,使得对称观测数据拥有相似的时间延迟.所以Data 3的声速结构会造成其坐标E分量更偏西,这就解释了为什么定位结果(表3)中Data 3的E分量相对于Data 1/2向西偏移了0.383 m左右,而N分量并无显著差异.同时也证明了网格构型解算的水平坐标易受到声速变化的影响,尤其是具有较长时间的观测数据.圆走航数据的水平坐标不受到影响的一个可能原因是其观测时间较短,声速变化的长周期部分没有产生较大的影响,对称点处的声速并无显著差异.在Xu等(2005)中的矩形测量与圆形测量实验中,实验结果表明矩形测量在削弱系统误差方面不如圆形测量有效,这一现象被解释为圆形测量在短时间内就可满足对称性的要求,这在一定程度上与本文结论是一致的.
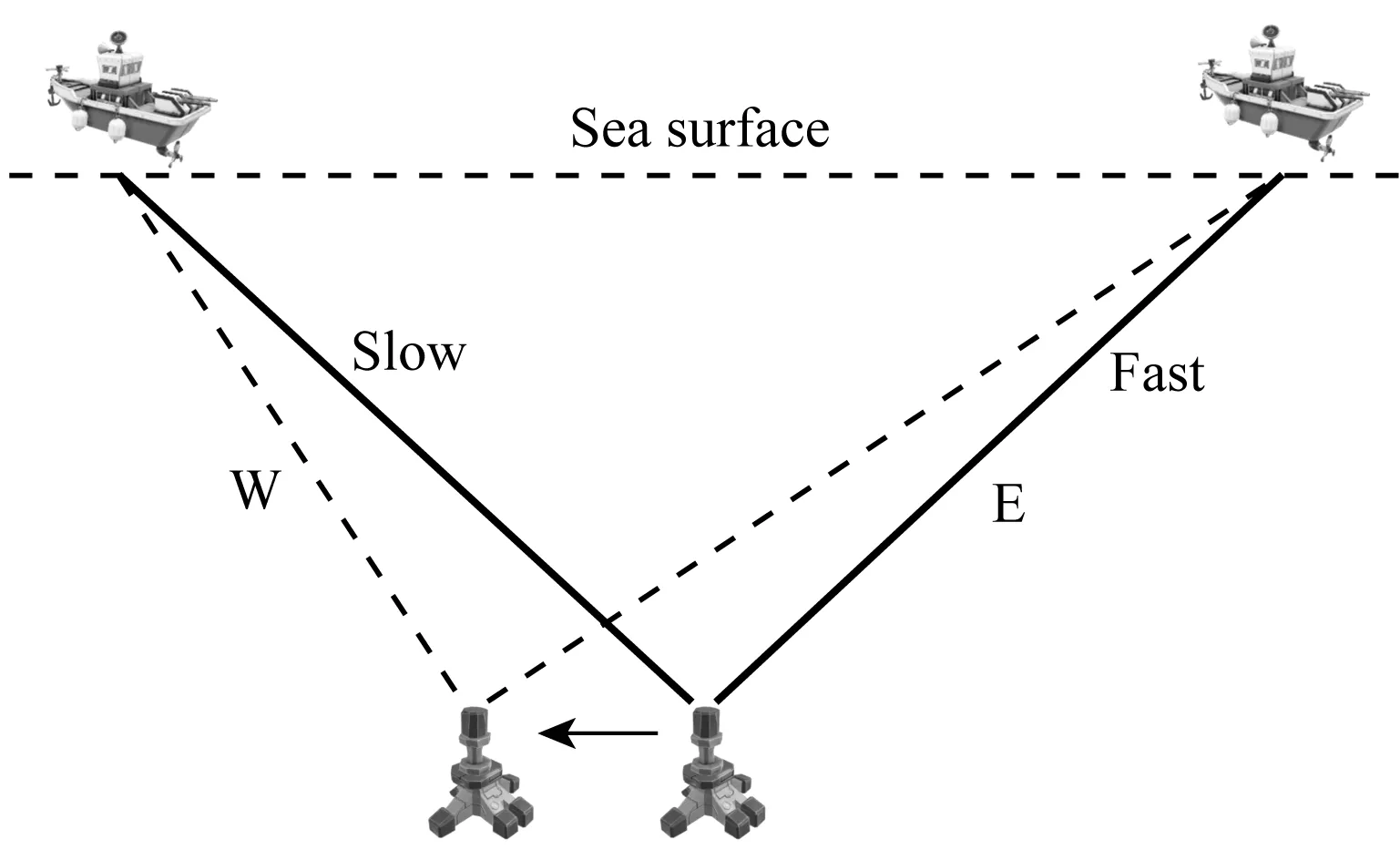
图11 声速对定位结果的影响Fig.11 Influence of sound velocity on positioning
图12显示了所有数据模型残差序列和直方图.这些直方图都大致遵循正态分布,残差序列无明显的系统趋势.但也可以看出不同时段内测量精度是不同的,距离海底应答器更近的观测数据具有更小的偶然误差.这一现象在图12c的残差序列中尤为明显.

图12 不同数据集的双程时间残差序列及直方图(a) Data 1; (b) Data 2; (c) Data 3.Fig.12 Round-trip time residual and histogram of different data set
4 结论
本文在双程声线跟踪方程的基础上,推导出了顾及声速扰动的海底定位模型,实现了海底应答器坐标与声速时空变化的联合估计.通过实测数据解算,可以得出以下结论:
(1) 顾及声速扰动的海底定位模型残差大致遵循正态分布,系统误差得到了较好的补偿,海底应答器定位精度优于10 cm.
(2) 声速结构表现出明显的日变化和内波引起的短周期波动特性.声速的整体时间变化小于1 m·s-1,整体空间变化小于0.1 m·s-1,空间梯度小于0.04 m·s-1·km-1.大部分观测时段内南北方向梯度明显大于东西方向梯度.
(3) 相比于圆走航数据,由网格构型数据估计的水平坐标易受到声速时间变化的影响.
致谢非常感谢编辑和审稿人的建议和意见.
