基于VMD-LSTM 的非侵入式负荷识别方法

王 毅，易 欢，李松浓，冯 凌，刘期烈，宋如楠

（1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.国网重庆市电力公司电力科学研究院，重庆 400014；3.国网重庆市电力公司营销服务中心，重庆 400014；4.中国电力科学研究院，北京 100192）

0 引言

随着社会的发展，电力成为社会的主要能源。电网是电力运输、分配和使用的载体。保持智能电网的稳定运行是电力系统规划和管理的根本目标[1]。负荷监测可以帮助电力公司获得用户的详细用电信息，分析用户用电信息可以为电力系统的规划和智能调度提供指导意见[2]。对电力用户来说，可以通过负荷监测结果分析自己的用电行为，制定合理的用电策略，降低用电成本，节约能源资源。侵入式负荷监测(Intrusive Load Monitoring,ILM) 和非侵入式负荷监测(Non-Intrusive Load Monitoring,NILM)是电力监控的两种手段。ILM 系统需在每个家用电器的前端安装测量传感器，用以实时的记录设备的用电信息，其成本与电器的数量成线性关系；NILM 由美国麻省理工学院的Hart[3]教授于20 世纪80 年代提出，仅通过家庭入口处的电流电压信息，采用算法得到各用电器的电气信息。与ILM 系统相比，NILM 系统有安装方便、成本低、保护隐私安全等优点。非侵入式负荷识别主要有两种实现方法，即事件法[4]和分解法[5，6]。事件法检测电器设备的启动/关闭事件，以事件的瞬态变化为特征判断电器的类型，从而推断电器的实时工作状态，实现电能的分解。分解法是直接从多负载叠加的电气特性分解为每个电器特性最可能的组合。但随着电器设备数量的增多，分解法的复杂度大大提高，而事件法则没有上述缺点。事件法的关键在于对电器产生的负荷投切事件进行准确分类。

文献[7]采用孪生神经网络结合空间凸包重叠率的相似性计算方法，在保证已知负荷的识别精度的基础上，引入迁移学习实现了未知负荷的识别。文献[8]采用电压和电流的总体变化作为负载特征，根据循环中电压电流变化的差异提取V-I 轨迹的特征，以带有附加注意模块的卷积神经网络进行负载识别，但特征提取步骤较繁琐且V-I 轨迹的训练占用计算资源大。文献[9]采用有功功率和无功功率作为第一层中识别负载的特征，以电流的三次谐波和五次谐波作为第二层中识别负载的特征，通过KNN 进行负荷的识别。文献[10]采用局部均值平均法(LMD)结合KNN 的方法，通过LMD 将有功功率进行分解，将分解得到的分量作为设备的唯一负载指纹，有效增加了相似负荷的识别率，但是对KNN 的K值以及LMD 的分解维数都需要根据经验得到，存在不确定性。文献[11]采用随机森林对负荷特征进行优选，再利用经过遗传算法优化的极限学习机进行负荷分类。文献[12]先采用有功功率和无功功率作为负荷特征，采用k-means 算法进行聚类，针对一阶段的识别盲区，构建卷积神经网络，以V-I 轨迹作为负荷特征进行二次识别，但模型训练时间长。文献[13]在电压满足一定条件的情况下采集负荷稳态波形作为负荷特征，利用动态时间弯曲(DTW)算法计算稳态波形与模板库的距离来识别负荷，但是在测量稳态波形时对电压有严格要求且对小电流设备的工作状态容易误判。

针对以上方法存在的缺陷，本文采用VMD 对归一化的单周期稳态电流信号进行分解，求分解后分量与归一化信号的相关系数，选相关系数最大的两个分量作为电器的负荷特征，输入训练好的LSTM 神经网络进行识别。该方法不仅提高了相似性负荷的识别率，且模型训练时间短，花费计算资源较少。通过PLAID 数据集和实验室采集数据进行仿真实验，证明了本文方法的有效性。

1 特征构建

1.1 VMD 算法原理

变分模态分解(Variational Mode Decomposition,VMD)是Dragomiretskiy K[14]等人于2014 年提出的一种新的非线性、非平稳信号的自适应分解计算方法。该方法认为各个IMF 分量都是集中在中心频率附近的窄带信号。根据IMF 分量的窄带条件建立约束问题来估计IMF 分量的中心频率和重构IMF 分量。

电流的原始信号为i(t),ik(t) 为经VMD 分解的K个离散模态分量,k=1,2,…,K。

算法分解步骤如下：

(1)应用Hilbert 变换获取每个模态分量ik(t)的单边谱，如式(1)所示：

式中：δ(t)为狄拉克函数。

(2)将每个模态分量ik(t)频谱搬移到相应基频带，如式(2)所示：

式中：ωk为ik(t)的中心频率。

(3)通过对各模态分量ik(t) 解调信号的高斯平滑方式估计各模态分量的带宽，构造式(3)所示的约束变分模型：

式中：∂t为对t求偏导。引入拉格朗日乘子λ和二次惩罚因子α，通过增广拉格朗日函数将上述等式约束优化问题等效为一个无约束优化问题，如式(4)所示：

采用交替方向乘子法ADMM 和Parseval 定理交替迭代更新，直至满足迭代终止条件：

式中：ε为求解精度。

求解过程中单个变量的更新表达式如式(6)、式(7)、式(8)所示：

式中：γ为噪声容忍度。

1.2 基于VMD 的特征构建

非侵入式负荷监测系统中，数据质量是影响识别精度的重要因素。且不同的采样频率、不同的采样设备得到的数据会有一定的不同。为减小不同采集设备采集数据的差异，本文对电流进行归一化处理，将电流归一化到(-1,1)范围。归一化按式(9)进行处理：

式中:inor代表归一化电流数据，imax为单周期内电流的最大值，imin为单周期内电流的最小值。

笔记本稳态电流经VMD 分解为5 个IMF 分量的波形如图1 所示。

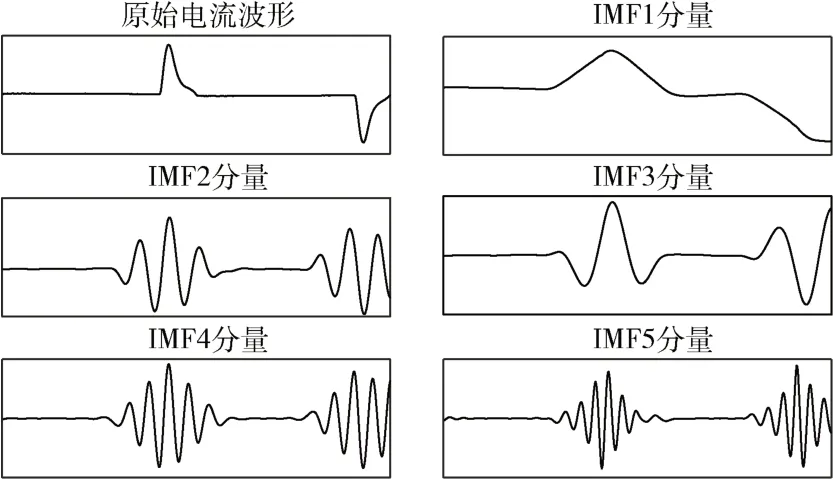
图1 笔记本原始电流及分量波形

计算各IMF 分量与归一化后电流信号的相关系数，将相关系数最大的两个IMF 分量合并为一维向量作为该负荷的负载特征。

笔记本的负荷特征曲线如图2 所示。横轴为采样点的个数，单周期的采样点为500，分解后的每个分量的采样点也为500，故合并后的特征的采样点为1 000。

图2 笔记本负荷特征波形

2 LSTM 网络模型及识别流程

2.1 LSTM 网络模型

在循环神经网络(RNN)的基础上引入了遗忘门、输入门和输出门控制每个细胞单元的状态得到长短期记忆神经网络（LSTM）[15]，它解决了RNN 梯度消失和梯度爆炸等问题。LSTM 的模型内部结构如图3 所示。

图3 LSTM 内部结构图

ft为遗忘门、Wf为遗忘门的权重矩阵；it为输入门，Wi输入门的权重矩阵；ot为输出门，Wo为输出门的权重矩阵。各计算公式如式(10)所示：

2.2 识别流程

负荷识别流程如图4 所示，首先经过稳态数据的采集得到设备的稳态电流，将稳态周期电流经VMD 分解，得到各分量波形；将与归一化后电流信号相关系数最大的两个分量拼接为一维负荷特征，输入训练好的LSTM网络进行负荷识别。

图4 负荷识别流程

3 算例测试及分析

本文采用基于Python 3.6 平台TensorFlow 2.0 的深度学习框架。硬件平台为Intel(R) Core(TM) i5-6500 CPU 3.2 GHz、8 GB RAM。

3.1 评价指标

本文采用混淆矩阵全面地评价分类结果。评价指标Pre代表当前样本的准确率，Rre代表召回率，F1代表准确率和召回率的平均评估指标[16]。计算公式如式(11)、式(12)、式(13)所示：

其中TP 表示真实和预测都为正类的数量；TN 表示实际和预测都是负类的数量；FP 表示实际为负类，但预测为正类的数量；FN 表示实际为正类，但被预测为负类的数量。

3.2 PLAID 数据集算例分析

PLAID 数据集，采样频率为30 kHz，该数据集记录了美国宾夕法尼亚州55 个家庭用户的用电数据，包括11 种不同的电器1 793 组电压、电流数据[17]。提取各个电器的180 个稳态周期的电流数据，经过VMD 分解后选择与归一化信号相关系数最大的两个分量作为负荷特征，构建成1×1 000 的一维负荷特征。文中训练数据集与测试数据集的比例为7:3，总数分别为1 386 和594。实验仿真结果绘制的混淆矩阵如图5 所示。

图5 PLAID 数据集LSTM 识别结果绘制的混淆矩阵

混淆矩阵中，纵轴表示用电设备的实际类别，横轴表示预测类别，矩阵中斜对角线上的数字表示正确识别的数量，其他位置的数字表示未被正确识别的数量。百分数表示当前类别数量占测试集总样本的比例，最右侧的百分数表示准确率，最下侧的百分比表示召回率。从中可以看到，各个电器的识别率都在96%以上，整体识别率达到了99%，说明本文方法有效。

3.3 与其他算法的对比

为了进一步说明本文方法的有效性，与其他负荷识别算法进行对比，表1 列出了各个算法的设备识别率，实验均在PLAID 数据集上进行。各算法的准确率如表1 所示。

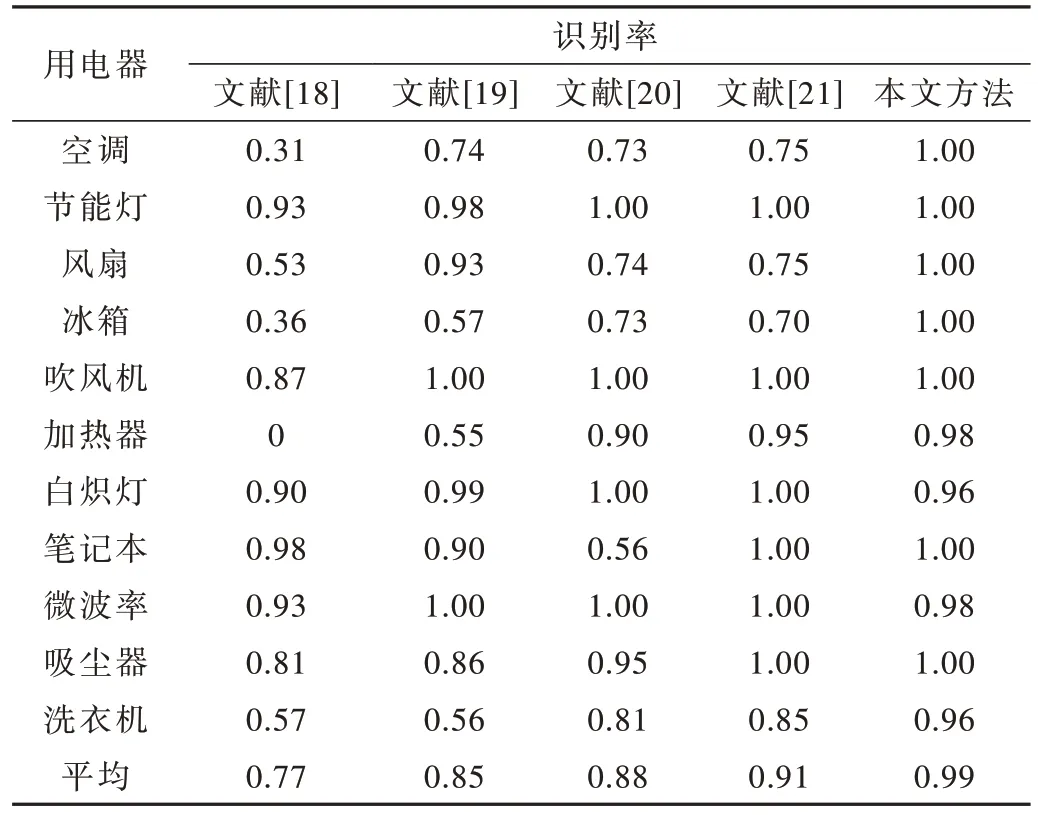
表1 与其他识别算法的识别率对比

其中文献[18]提取V-I 轨迹图像的轮廓特征，利用这些特征计算椭圆傅里叶描述符作为负荷特征，利用多层感知机进行分类。文献[19]采用自动选择设备特征的递归特征消除算法，以随机森林作为分类算法。文献[20]采用稳态、暂态相结合的负荷特征，利用基于PCA 的辨识分类算法进行分类。文献[21]使用V-I 轨迹图像结合功率作为负荷特征，以BP 神经网络进行分类。由表1 可知，相比于参考文献中的方法，本文方法采用VMD 分解单周期稳态电流，计算分量与归一化电流信号的相关系数，挑选相关系数最大的两个分量作为负荷特征，增加了算法的辨识能力。

3.4 实验室自采数据集实验仿真及分析

实验室采集数据采用1 000:1 的电流互感器，Pico-Scope 5000 series 进行数据采集。用电设备信息如表2所示。

表2 实验室所用设备信息

实验室自采数据集采样频率为5 kHz，包括6 种电器共1 080 个电流周期数据。经VMD 分解后选用与归一化电流信号相关系数最大的两个分量拼接为1×200 的一维向量作为负荷特征。与PLAID 数据集一样，训练集与测试集的比例为7:3，训练集和测试集的样本总数分别为756、324。经训练后的LSTM 模型分类效果如图6 混淆矩阵所示。

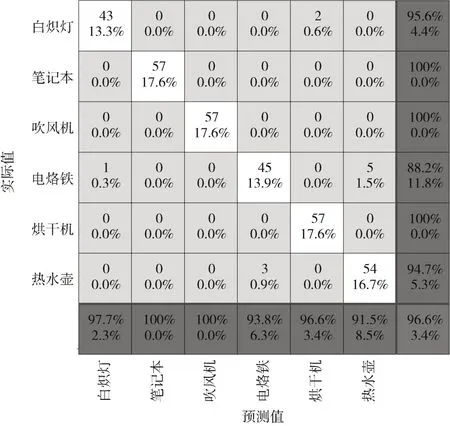
图6 实验室采集数据集LSTM 识别结果绘制的混淆矩阵

3.5 数据集结果差异分析

整体来看，该方法在PLAID 数据集上的识别率高于实验室采集数据的识别率，分析主要的原因在于PLAID数据集相似性负荷较少，而实验室采集的数据相似性负荷较多。另外一方面是采样频率的不同，PLAID 的采样频率为30 kHz，而实验室采集的数据是5 kHz，采样频率越高，则采集得到的数据含有的负荷信息就会更多，经VMD 分解后会有更多的特征信息。

4 结论

针对相似性负荷识别率较低的问题，本文提出一种VMD 结合LSTM 的负荷识别方法。先将归一化的单周期稳态电流用VMD 进行分解，再计算各分量与归一化电流信号的相关系数，将与归一化信号相关系数最大的两个分量作为负荷特征，采用LSTM 神经网络进行识别。在公开数据集PLAID 上进行仿真验证，仿真结果的识别率为99%，表明本文方法的有效性。与其他负荷识别算法对比，本文所提方法可以得到更多的负荷特征信息，可以有效地提高识别率。最后在实验室采集的数据集上进行了仿真验证，96.6%的识别率充分说明本文所提方法拥有良好的鲁棒性。