基于平均电流模式的同步Buck 数字电源设计研究

李键文，潘永雄，徐家锐，梁 康

（广东工业大学 物理与光电工程学院，广东 广州 510006）

0 引言

同步Buck 变换器在传统Buck 变换器基础上结合了同步整流技术，具有效率高、体积小和拓扑结构简单等优点。同步Buck 变换器控制可以采用模拟控制或数字控制两种方式，相对于传统模拟控制而言，数字控制具有较强的适应性和灵活性[1]，数字控制的实现要求设计者具备使用高性能数字控制芯片的能力、仿真分析控制算法的能力以及良好的自动控制理论基础。

文献[2]详细介绍了同步Buck 数字电源的硬件电路设计，包括主电路器件选型、驱动电路设计和辅助电源电路设计。文献[3]基于平均电流模式同步Buck 数字电源，讨论了电压模式和电流模式下的闭环控制器设计，提出在PI 补偿器的基础上增加一个高频极点以降低系统的高频噪声。文献[4]提出了同步Buck 电路的双闭环PI 参数计算方法，对引入补偿器后的系统开环传递函数按照系统型别进行补偿器优化设计。本文在以上研究的基础上结合理论分析和Matlab/Simulink 软件仿真，分析了同步Buck 的环路设计条件，确保变换器在严苛条件下仍能稳定运行，详细阐述了两种电压电流双闭环PI参数设计方法，提出一种基于电流环简化的电压环设计方法，提高了数字环路设计的灵活性，并以ST 公司的STM32G474 处理器为主控芯片，设计了一款基于平均电流模式的同步Buck 数字电源，实现高精度恒压恒流电源功能，具有一定的参考意义和实用性。

1 系统结构框图

系统结构框图如图1 所示，同步Buck 数字电源由主电路、辅助电源、驱动电路、采样电路以及STM32G474 主控电路构成。在本设计中以STM32G474作为主控芯片，利用其高精度定时器模块产生所需的互补PWM 信号；驱动电路部分采用半桥栅极驱动器芯片SI8233，该驱动器带有死区时间可编程功能，能有效避免上下管共通现象；输出电压和输出电流的采样电路均采用差分放大的方式实现，能较大程度地减小开关电源的高频噪声对采样电路的干扰，使用低零偏运算放大器RS8559 可以提高电流转化精度，结合ADC 模块将采集的信号进行运算处理，以达到恒压恒流输出的目的；辅助电源部分采用XL7005A、AMS1117-5 和AMS1117-3.3 分别变换产生12 V、5 V 和3.3 V 供电，并为驱动电路、采样电路、主控芯片以及ADC 模块参考电压供电。

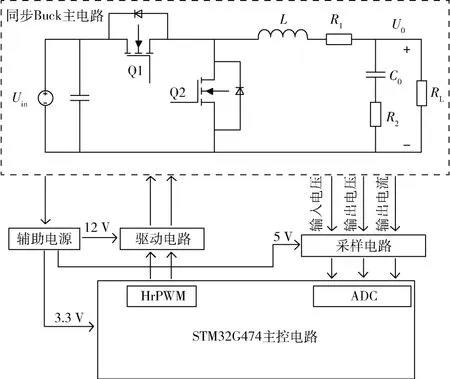
图1 同步Buck 数字电源系统结构框图

2 双闭环控制器设计

Buck 变换器的小信号交流等效电路为二阶电路，当系统采用电压单环控制时，若变换器输入电压或输出负载发生变化，系统只有在检测到输出电压发生变化后才触发电压控制环动作，因此系统的动态响应相对较慢，再加入电流反馈环后，实现电压、电流双环控制就能够从主电路中获取更多的状态信息，从而得到比单环控制更好的动态响应性能[5]。常用的电流控制模式有峰值电流模式和平均电流模式两种，其中峰值电流模式能够实现逐周限流保护，具有更高的可靠性，但在占空比大于50%时，需要增加斜坡补偿以消除次谐波振荡现象。次谐波振荡现象的产生是由于PWM 比较器的两个输入端信号发生不匹配，峰值电流模式采用斜坡补偿来调节，而平均电流模式则采用一个高增益电流反馈来调节[6-8]。

2.1 同步Buck 环路设计条件

在环路设计前需要先建立Buck 变换器的动态数学模型，小信号分析法是目前常用的方法，其基本思想是：假设变换器系统运行在某一稳态工作点附近，当施加小信号扰动时，电路状态变量的小信号扰动量之间的关系会呈现出线性系统的特性，因此在研究变换器系统在某一个稳态工作点附近的动态特性时，可以把它近似为线性系统，并利用经典控制理论进行补偿器设计。采用小信号分析法[7,9]可以得到Buck 变换器从占空比(s)到电感电流(s)的传递函数Gid(s)、从占空比(s)到输出电压(s)的传递函数Gud(s)和从电感电流(s)到输出电压(s) 的传递函数Giu(s)，相应传 递函数 分别用 式(1)、式(3)和式(4)表示：

本设计是基于平均电流模式下的同步Buck 数字电源，主要设计参数如下：输入电压Uin为12 V～30 V，输出电压UO为5 V～15 V，额定输出电流IO=5 A，目标效率η=95%，开关频率fSW=200 kHz。在式(1)～式(4)中，Δ 为式(1)和式(3)的分母特征多项式；RL为负载电阻；L为输出滤波电感，电感值为22 µH，等效直流电阻R1约为30 mΩ；CO为输出滤波电容，电容值为100 µF，等效串联电阻R2约为10 mΩ。

在式(3)中，传递函数Gud(s)的直流增益正比于输入电压，通过Matlab 软件绘制Gud(s)在不同输入电压下的波特图如图2 所示，当输入电压升高时，幅频曲线上移，频宽变大，但相频曲线并没有改变，造成相位裕量下降，影响系统稳定度；在式(4)中，传递函数Gid(s)的直流增益反比于负载电阻R，即当负载电阻减小时也会造成相位裕量下降。因此为了保证系统有足够的相位裕量，应该按最高输入电压和最小负载电阻来进行补偿器设计，在本设计中以最高输入电压30 V 和最小负载电阻1 Ω 作为同步Buck 的环路设计条件。

图2 不同输入电压下Gud(s)的波特图

2.2 两种双闭环PI 补偿器参数设计方法

2.2.1 先补偿电流环后补偿电压环

基于平均电流模式的同步Buck 变换器控制系统结构图如图3 所示，其中Gu(s)和Gi(s)分别为电压环和电流环PI 补偿器的传递函数；Gid(s)为占空比到电感电流的传递函数；Giu(s) 为电感电流到输出电压的传递函数；Ki(s)和Ku(s)分别为电感电流采样网络和输出电压采样网络的传递函数，在本设计中电感电流采样和输出电压采样均使用差分放大器实现，Ki(s)=0.495，Ku(s)=0.061；Gm(s) 为脉宽调制器的传递函数，Gm(s)=1/3.3。

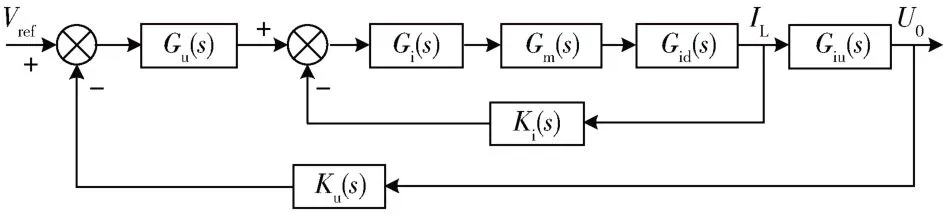
图3 平均电流模式同步Buck 变换器控制系统结构图

采用电压电流双闭环控制时，电压补偿器的输出需作为电流补偿器的基准输入，为保证电流环基准的稳定，电流环的穿越频率需高于电压环的穿越频率。穿越频率越高，系统响应速度越快，但相位裕量相对越低，影响控制系统的稳定度。因此，电压环也被称为慢环，电流环被称为快环。对于数字电源而言，工程上通常将补偿后电流环开环传递函数的穿越频率fC1设计为开关频率fSW的1/10～1/20[5]。在本设计中将补偿后电流环的穿越频率fC1取为开关频率fSW的1/10，即fC1=20 kHz，将补偿后电压环的穿越频率fC2取为fC1的1/4，即fC2=5 kHz。

采用PI 补偿器对电流环进行补偿设计，定义电流环PI 补偿器的被控对象传递函数为Ai(s),电流环开环传递函数为Ti(s)，则有：

PI 补偿器为单极点单零点形式，引入了一个零极点和一个左半平面零点ωZ1，其传递函数可表示为：

与模拟控制相比，数字控制会引入额外的延时而造成相位损失[4]，例如ADC 采样零阶保持器所引入的延时和ADC 采样到实际占空比更新所引入的延时。因此，设计时应预留足够的相位裕量。在本设计中定义补偿后的电流环相位裕量为70°，则PI 补偿器的左半平面零点ωZ1在穿越频率fC1处所需要产生的相位超前角度θ1应满足：

式(8)中的-90°相移为PI 补偿器的零极点作用，计算得到θ1=69.019°。对应的零点位置应满足：

又根据穿越频率的定义，电流环开环传递函数Ti(s)在穿越频率fC1处的增益为0 dB，则：

由式(9)和式(10)可得电流环PI 补偿器GI(s)的左半平面零 点位置ωZ1=2πfZ1=4.819 × 104rad/s，系 数K1=2.687 × 104。模拟PI 补偿器的传递函数还可以表示为：

在式(11)中，KP1和KI1分别为比例环节和积分环节的系数，对比式(7)和式(11)可以得到KP1=0.558，KI1=2.687 × 104。电流环补偿前后的波特图如图4 所示，可见加入电流环PI 补偿器后，电流环的穿越频率和相位裕量均达到目标值。完成电流环补偿器设计后，可以将图3 所示的双闭环控制系统转化为包含电流环作用的电压单环控制系统，在本设计中设定补偿后电压环穿越频率fC2=5 kHz，相位裕量为70°，定义电压环补偿器Gu(s)的传递函数为：

图4 电流环补偿前后的波特图

电压环PI 补偿器的参数设计方法与电流环PI 补偿器一致，计算得 到：ωZ2=2πfZ2=2.206 × 104rad/s，K2=4.633 × 105，KP2=20.996，KI2=4.633 × 105，图5 为电压环补偿前后的波特图，补偿后的幅频曲线在低频段具有较大的增益，有利于减少稳态误差；在中频段以-20 dB/(°)的斜率穿越0 dB 线，且占据较宽的频率范围，保证控制系统有足够的相位裕量。

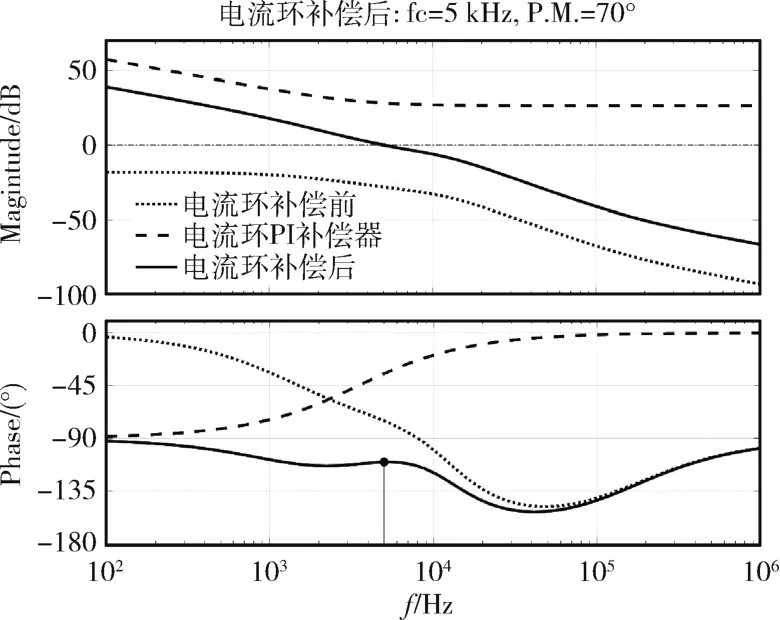
图5 电压环补偿前后的波特图

2.2.2 基于电流环简化的电压环设计

由于电流环的带宽高于电压环，当f＜fC1时，满足|Ti(s)| ＞＞1，可以对电流环进行简化，电流环闭环传递函数Gi_close可以表示为：

基于电流环简化的同步Buck 控制系统结构图如图6 所示，对简化后的控制系统进行电压环PI 补偿器设计，得到PI 参数为：比例系数KP3=21.018，积分系数KI3=5.403 × 105。对比可知基于电流环简化所计算得到的电压环PI 参数KP3和KI3与2.2.1 节先补偿电流环后补偿电压环所计算得到的PI 参数KP2和KI2接近，提高了双闭环PI 补偿器设计的灵活性。

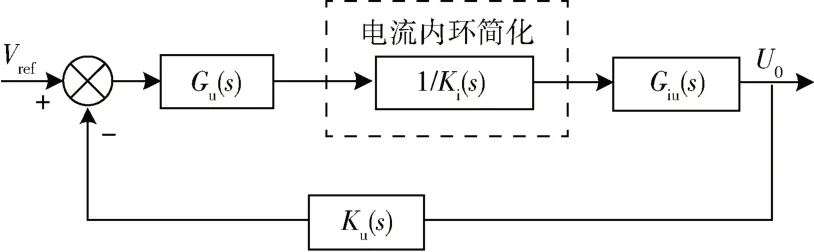
图6 基于电流环简化的同步Buck 控制系统结构图

3 系统软件设计

控制系统以STM32G474 作为主控芯片，STM32G4系列基于一颗170 MHz 且内部集成FPU 和DSP 指令的 ARM Cortex-M4 高速内核，相比STM32F3 系列具有更强大的性能[10]。为简化系统软件架构，同时增加系统软件的可移植性，本设计采用中断事件触发和状态机运行思想来构建同步Buck 软件系统。系统软件架构如图7所示，控制器在上电或复位后，会先初始化时钟和相关外设，随后进入空循环状态，等待中断事件触发。软件主体主要由两个中断构成，分别为100 kHz 中断和200 Hz中断，其中100 kHz 中断的优先级设为最高，同时在中断运行过程中启用中断嵌套功能，即优先级高的中断可以打断优先级低的中断。软件在100 kHz 中断服务程序中完成ADC 数据获取、PI 补偿器运算、占空比更新和过流保护等对时效性要求高的程序，并通过DMA 实现ADC数据采样，由于DMA 为直接存储器访问，其无需CPU 干预即可直接控制传输，可以提高控制芯片的时间资源利用率。200 Hz 的中断优先级较低，主要运行程序控制状态机函数，状态机包括初始化状态、等待状态、软启动状态和正常运行状态。状态机运行图如图8 所示，程序在初始化状态下完成相关参数基准值的设定，然后进入空闲状态，在等待一定时间并查询无故障情况后进入软启动状态，软启动结束后进入程序正常运行状态，若在软启动或正常运行过程中发生故障或触发保护时，则程序会进入故障状态，等待故障恢复后电源返回空闲状态。

图7 系统软件架构

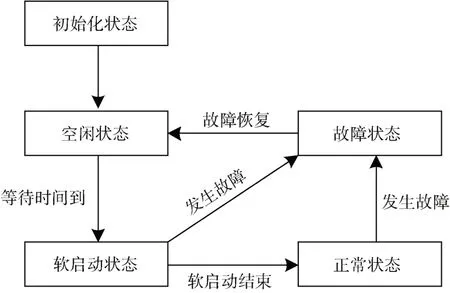
图8 状态机运行图

4 仿真分析及实验结果

4.1 仿真分析

利用Matlab/Simulink 软件对所设计的Buck 变换器进行仿真验证，电路仿真模型如图9 所示，在电流环控制回路中，以频率固定的三角波信号作为载波信号并将其与电流环PI 补偿器输出信号进行比较后产生PWM 控制信号。当电流环PI 补偿器输出信号高于载波信号时，比较器输出高电平信号，且载波信号在高电平信号的中点时刻达到最小值。当Buck 变换器工作在CCM 模式时，利用采样保持模块对该时刻的电感电流信号进行采样，便能得到电感电流的平均电流值，即该时刻可以作为平均电流控制模式下的电流采样时刻。图10 和图11分别为仿真模型在输入电压发生跳变（输入电压从30 V切换至15 V）和输出负载发生跳变时（输出负载从25%切换至100%）的环路响应波形，仿真结果表明该电源变换器在输入电压或输出负载发生跳变时电流环响应迅速，输出电压过冲/下冲小，调节时间短，环路设计合理。

图9 基于平均电流模式的Buck 电路仿真模型

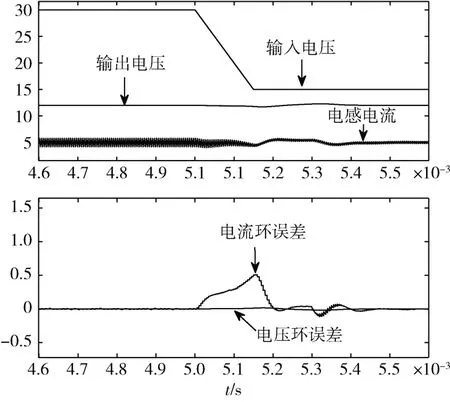
图10 输入电压跳变时的环路响应波形

图11 输出负载跳变时的环路响应波形

4.2 实验结果

根据前述的设计条件制作了一台实验样机，实验样机在输入电压为30 V，输出电压为5 V～15 V，输出负载为0.5 A～5 A 时的效率曲线如图12 所示，实测效率高达95%，负载调整率小于5%，系统能长时间稳定运行，符合设计要求。

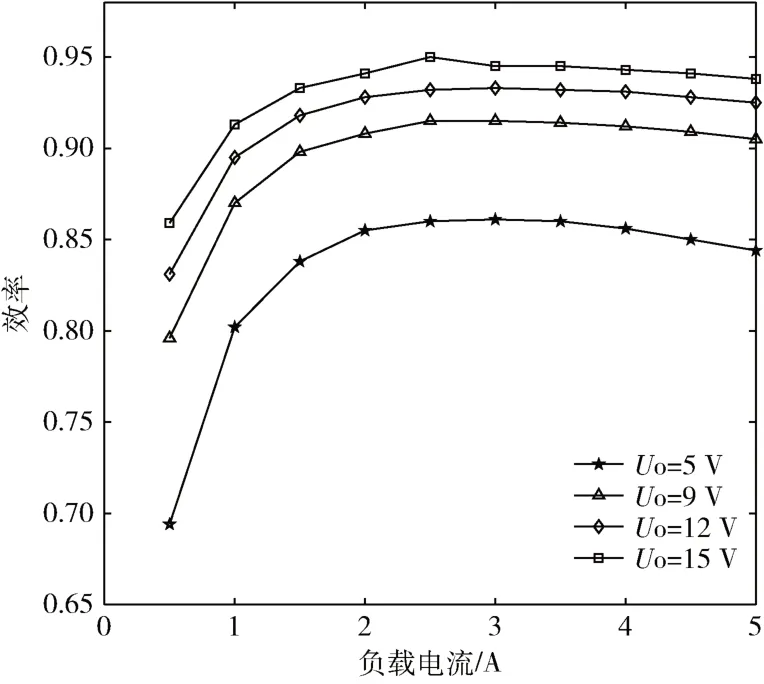
图12 效率曲线

5 结论

本文针对平均电流模式下的同步Buck 数字电源，结合理论分析和Matlab/Simulink 软件仿真，分析了同步Buck 变换器的环路设计条件，对双闭环PI 补偿器进行了详细设计，并提出了一种基于电流环简化的电压环设计方法，提高了数字环路设计的灵活性。基于高性能主流MCU 芯片STM32G474 实现了变换器的双闭环数字控制，搭建了实验样机。仿真及实验结果表明系统具有效率高、动态响应快和鲁棒性强等特点，实现了高精度恒压恒流功能，具有一定的应用价值。