基于多体动力学的海底管线终端布放过程分析❋

樊莹莹，常宗瑜,2，郑中强，张博文，赵 林❋❋

(1.中国海洋大学工程学院，山东 青岛 266100；2.中国海洋大学 山东省海洋工程重点实验室，山东 青岛 266100)

水下生产系统因具有适应性强、占地面积小、灵活度高以及开采效率高等优点，广泛应用于深海油气开发工程中。海底管线终端(PLET)用于连接管道和水下生产设施，高质量的安装保障着水下油气运输过程，所以对其安装过程进行深入研究有着重要的现实意义[3]。

20世纪70年代，随着海洋油气开发的作业深度逐渐增加，国外各大石油公司对深水无潜海管回接技术开始了深入研究[4]。发展至今，国外PLET的安装深度记录在不断刷新，最深的PLET工作深度已达到2 926 m[5]。国内对于PLET安装的研究开始较晚，2012年，周美珍[6]等对流花4-1海管项目中PLET建造和安装的要求进行了阐述，这是国内第一次应用深水PLET。为了给实际安装提供理论技术支持，Liu等[7]在三维空间中研究了下端焊接有管道并通过吸力桩绕线牵引的PLET装置，建立了安装系统的数学模型及算法，并举例说明了安装工程中计算管道和牵引线力学行为的迭代过程。尹汉军等[2]对PLET的安装过程进行了介绍，并对整个过程中的关键位置进行了静态分析，还根据计算结果对PLET的安装过程进行了优化。PLET下放过程中缆索的动力学建模及分析是进行布放操作研究的重要部分。

现今针对于PLET安装过程的研究主要为静力学分析，对其安装过程的动态分析研究较少。本文基于多体运动学方法建立安装过程分析模型，采用多刚体添加轴套力的方式模拟钢丝绳柔性[8]，与PLET简化模型连接后，进行铺设安装的仿真分析，然后综合考虑流速、水深、PLET尺寸等因素的变化对绳索张力、伸长量以及落点偏移的影响，研究结果对于PLET实际安装有参考意义。

1 PLET结构及安装

PLET通常由防沉板、管道及各结构组件、支撑结构与扼套(YOKE)几部分组成，如图1所示。防沉板用来保证整体稳定性以及减少海底沉降与滑移，支撑结构支撑PLET的所有组件，扼套与支撑结构铰接，减少布放过程中的扭转[1]。

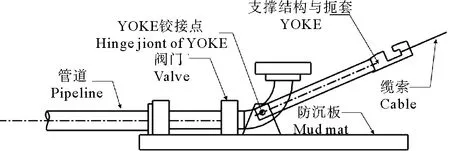
图1 PLET结构简图

PLET的安装方式可分为直接吊装与铺设安装两种[9]。直接吊装法是通过作业船将PLET结构直接吊装下放至海底，然后将连接的管汇结构也下放至海底进行组装，管线尺寸以及结构形状不受限制，但是需要在海底进行两端的海管连接，操作难度大；铺设安装法中，海底管线已经焊接到PLET管道连接端，PLET随管线一同布放，海管与PLET在水上提前进行焊接节省了水下与管线的安装时间，但是管线尺寸受铺管船限制较大。在深水项目中，为了减低施工成本，越来越多的PLET安装采用铺设安装的方式，铺设安装法是PLET安装的未来趋势[10]。在本文中，主要对铺设安装的PLET进行研究，了解PLET在安装过程中的力学性能。PLET进行铺设安装时的安装过程如图2所示，Antani等[11]对在Neptune进行的PLET铺设安装过程进行了详细的介绍：首先在安装前检查所有阀门处于关闭状态；其次将PLET从安装船甲板吊起并倒置转移到悬挂架上；然后将PLET与悬挂架下方的管道进行焊接、涂敷涂层等操作；最后将PLET与管道一同移至A字架进行安装下放操作，直至安装至海床上。

(从左到右。From left to right.)

2 理论分析与模型构建

依据上文实际安装过程建立仿真模型，对整体安装系统在海洋环境中的受力进行分析，缆索、PLET及管道受力(单位：N)包括：重力G、浮力B、水动力FD、惯性力I、缆索张力T以及管道张力Tp。

本文对完全入水后的安装过程进行考虑，故结构物所受重力与浮力始终不变，浮力的表达式为：

B=ρgV。

(1)

式中:ρ为流体密度，取1 025 kg/m3；g为重力加速度，数值取9.806 65 m/s2；V为PLET排水体积，m3。

进行缆索及管道建模时，可采用添加轴套力方法，在ADAMS软件中分别将其划分为i、j段刚体，并在刚体之间添加轴套力，使其与实际缆索、管道的运动状态吻合，轴套力通过在两刚体间添加力与力矩来定义[12-13]，利用此方法建模，便于在缆索及管道上添加水动力。在安装过程中，水下结构物受到的流体阻力以及惯性力对布放过程有着重要的影响。在本文中，依据小尺度结构物的Morison方程进行流体阻力和惯性力计算[14],考虑安装过程中各结构物和水流的相对速度，则缆索微元、PLET及管道微元受到的流体阻力以及惯性力分别为：

(2)

(3)

式中：FDci为缆索微元所受流体阻力，单位：N;FDPLET为PLET所受流体阻力，单位：N;FDpj为管道微元所受流体阻力，单位：N;Ici为缆索微元所受流体惯性力，单位：N;IPLET为PLET所受流体惯性力，单位：N;Ipj为管道微元所受流体惯性力，单位：N;CD为阻力系数，无因次，在本文中阻力系数取0.78；Cm为附加质量系数，无因次，在本文中取2.0；ρ为流体密度，单位：kg/m3；Ac为缆索微元截面积，单位：m2；APLET为PLET截面积，单位：m2；Ap为管道微元截面积，单位：m2；U为水流速度分布矢量，单位：m/s；vci为缆索微元速度矢量，单位：m/s；vPLET为PLET安装时速度矢量，单位：m/s；vpj为管道微元速度矢量，单位：m/s；Vc为缆索微元体积，单位：m3；VPLET为PLET截面积，单位：m3；Vp为管道微元截面积，单位：m3。

在Morison方程中，流体相对速度与海底流速变化密切相关，海底流速在无法进行详细测量时，流速随深度的变化可由以下分布规律计算[15]：

(4)

式中：vtide,0为静止水面流速，单位：m/s；h为深度，取正值，单位：m；z为距离水面距离，向上为正，单位：m；α为系数，一般取1/7。以顺流状态为例，该分布规律的流速剖面图如图3所示。

综合水下结构物受力，建立PLET安装过程中动力学方程：

(5)

式中：mci为单位缆索微元质量，单位：kg；mPLET为PLET质量，单位：kg；mpj为单位管道微元质量，单位：kg。

依据上文中建模理论建立PLET布放动力学仿真模型进行仿真分析，下放过程中的坐标系及下放流程简图如图3所示，以缆索与PLET连接点为坐标原点，水平面方向为x轴，垂直水平面方向为z轴，安装船沿x轴正向移动，PLET随安装船移动向z轴负向布放，PLET上YOKE连接缆索，下端与管道焊接，PLET上YOKE与防沉板间角度为θ。PLET简化模型与管道、缆索的参数如表1所示，安装地点水深约180 m。

图3 下放过程阶段示意图

表1 PLET简化模型及管道缆索参数

3 模型验证

Gilchrist[18]介绍了一种PLET安装过程的静态简化分析方法，在分析时进行如下假设：管道和缆索不受剪应力；忽略流对结构物的作用力；管道采用悬链线模型。对PLET进行静力平衡分析，如图4所示。

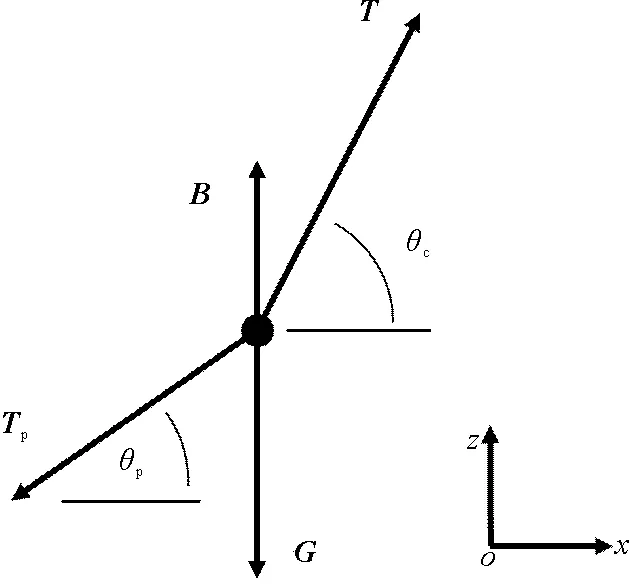
图4 PLET静力平衡简图

在x轴和z轴方向进行受力分析：

∑Fx=T·cosθc-Tp·cosθp=0;

(6)

∑Fz=T·sinθc-Tp·sinθp+B-G=0。

(7)

式中:Fx为x轴方向受力，单位：N；T为缆索张力，单位：N;Tp为管道张力，单位：N;Fz为z轴方向受力，单位：N；B为浮力，单位：N；G为重力，单位：N。

管道建模采用悬链线模型，通过悬链线方程计算管道内部张力。截取一个管道微元进行受力平衡分析，推导出管道的悬链线方程为：

(8)

式中：TO为管道内部轴向力的水平分量；w为单位管道微元受到的重力与浮力的合力。二者单位皆为N。

结合梁的曲率理论以及管线的曲率半径和应变的关系可得到管道轴向力水平分量的计算公式[17]：

(9)

对下放过程进行静态分析，将其假设为9个阶段，根据式(8)、(9)分别计算该九个阶段的管道内部的静态轴向应力，代入式(6)、(7)可得到绳索内部的静态轴向应力，然后将各个阶段计算得到的张力绘成曲线，将计算结果曲线与模型的动力学仿真分析结果进行对比，如图5、6所示，由于在计算中忽略了水动力以及流对于结构物的影响，所以绳索内部张力的计算结果略小于仿真结果，管道内部张力吻合较好，计算结果整体趋势相同，所以模型可用于研究。

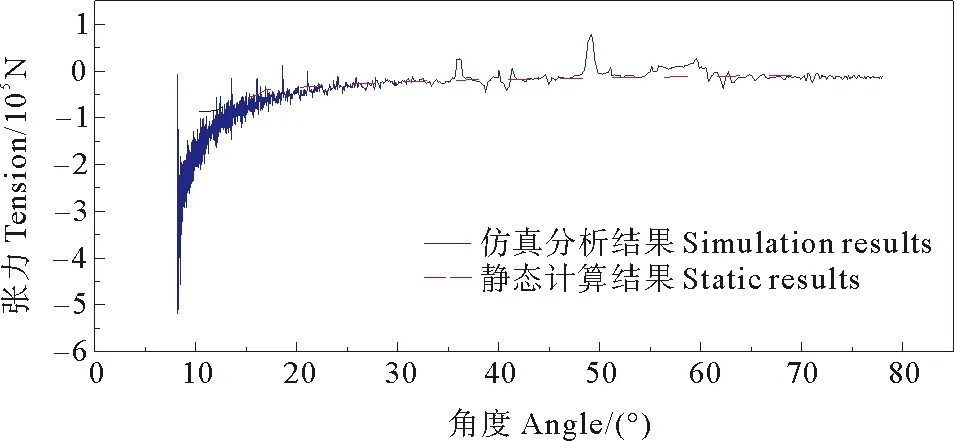
图5 管道张力随下放角度变化

图6 绳索张力随下放角度变化

4 动态仿真及结果讨论

4.1 静水下放结果分析

在流速为0 m/s时，即静水状态下进行下放，安装至约180 m水深处。图7为截取动态仿真过程中几个时刻下PLET、船体、缆索及管道状态的云图叠加，从图中可直观地看出布放过程中各结构的状态，可对布放过程有较直观的了解。

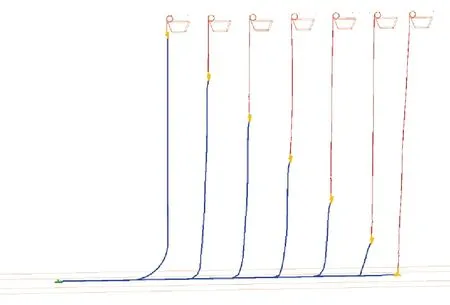
图7 下放轨迹变化

下放过程中竖直方向上位移响应曲线如图8所示，速度变化如图9所示，PLET进行布放时一般要求速度不超过1 m/s，文中为了缩短仿真时间，设定PLET下放速度约为1 m/s。安装时，初始释放点的速度变化较大，然后恢复稳定，以约1 m/s的速度下放，直至到达海床。图10为YOKE与防沉板间的角度θ在布放过程中的变化，在实际布放操作中，需要添加浮筒等结构来确保PLET不会产生较大扭转以及正向下放到海床上，从图中可以看出，YOKE与防沉板间的角度θ随PLET下放深度的增加逐渐增大，直至安装至海床，最后打开约80°。

图8 PLET竖直方向位移时间历程

图9 PLET竖直方向下放速度

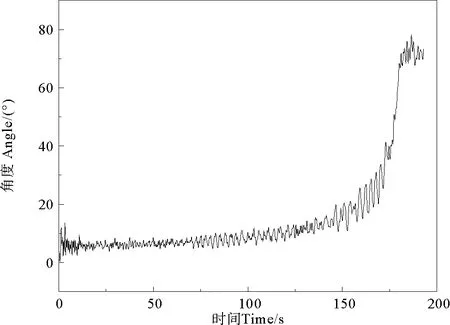
图10 YOKE与防沉板间角度θ时间历程

图11为静水状态下缆索张力时间历程，由图可知，初始释放阶段，缆索由松弛突然变为紧绷状态，张力产生突变，最大约为1.5×106N，从张力图的拟合曲线中可以看出，张力逐渐减少，从约5.0×105N减少到约3.0×105N，这是由于PLET下端连接铺设至海床的海管，缆索承担的质量逐渐减少，张力也逐渐减少。图12为管道张力时间历程，管道张力随PLET下放呈现逐渐减小的趋势，由管道张力的拟合曲线可知，力由约3.0×105N减小到约0。

图11 缆索张力时间历程

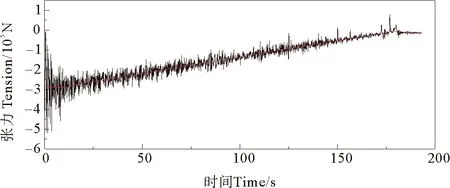
图12 管道张力时间历程

4.2 不同流速下PLET安装仿真分析

PLET在水下进行安装时，流速是重要的影响因素，会对安装结果产生各方面的影响，分别取南海流花海域以下几种海况流速条件[16]进行仿真安装分析，下放速度与静水安装时相同。

4.2.1 顺流状态下安装 设置流速方向与船体前进方向相同，流速分布规律按照式(4)计算，流速剖面图如图3所示，图13、14分别为缆索张力与管道张力随时间变化情况，更改流体速度后，缆索内部张力和管道张力在流速变化后整体趋势未产生较大变化，且数值上与静水下放时较为接近，可以得知：流速对张力的影响较小。

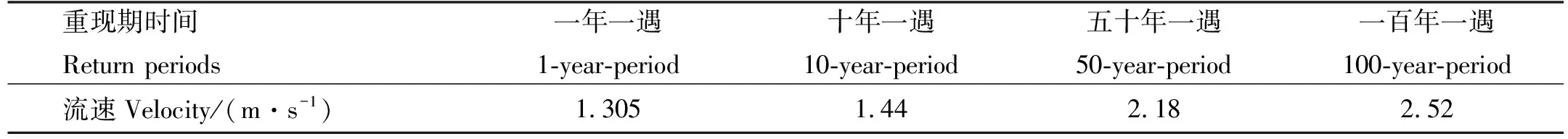
表2 南海流花海域海况条件

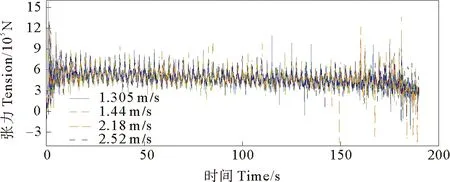
图13 不同顺流流速下缆索张力时间历程

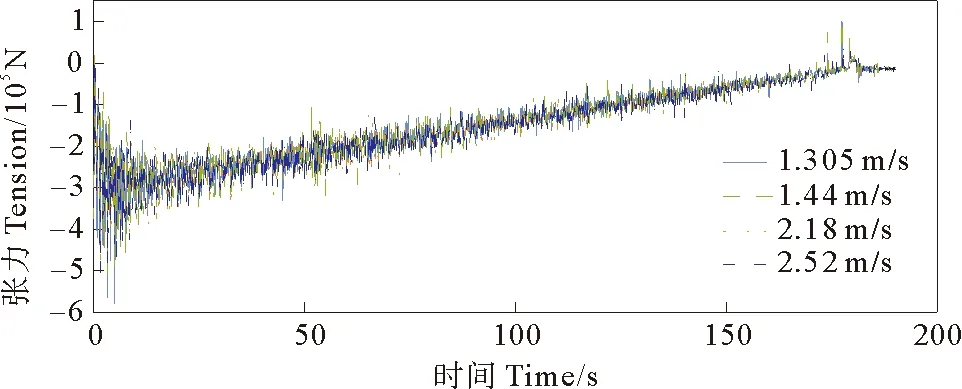
图14 不同顺流流速下管道张力时间历程

PLET在进行安装时，还应考虑的因素有弹性缆索在自重、PLET质量以及管道质量的影响下产生的伸长量以及PLET在安装至海床时产生的落点的偏移。表3为不同流速下放至同一深处海床时，缆索伸长量的变化，可以从表中看出，缆索的伸长量随流速增大几乎没有明显变化，流速对其影响较小。表4为不同流速下PLET在安装至海床时产生的偏移，表中计划安装位置为系统模型中始端PLET与终端PLET之间的距离。在与PLET横向安装方向一致的顺流流速方向作用下，流速越大，PLET落点的偏移量越小，且越接近既定安装位置，但也要综合考虑流速对安装船定位的影响，并非顺流流速越大越便于安装。

表3 不同顺流流速下缆索伸长量

表4 不同顺流流速下PLET落点偏移

4.2.2 逆流状态下安装 更改流速方向为与船体前进方向相反，流速分布规律与顺流相同，再次进行安装仿真，得到结果如图15、16所示。图15、16分别为逆流下的缆索张力和管道张力随时间变化情况，流速对于张力影响较小。

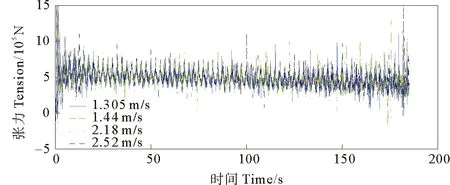
图15 不同逆流流速下缆索张力时间历程

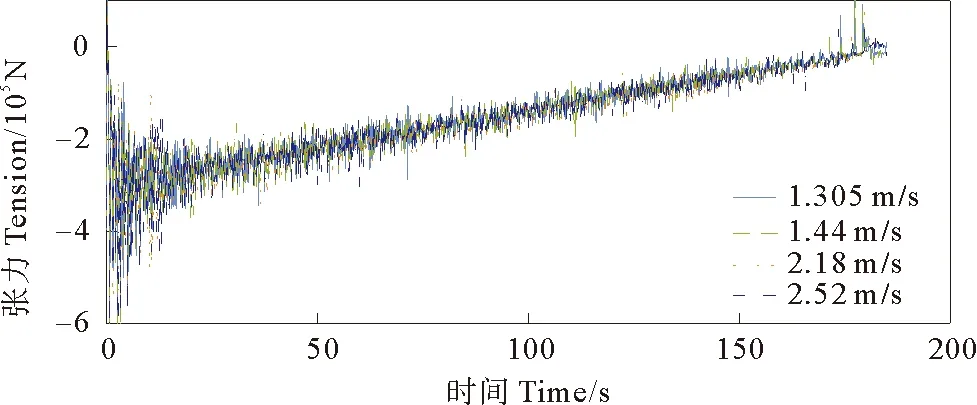
图16 不同逆流流速下管道张力时间历程

表5为逆流下安装至同一深度海床时，缆索伸长量的变化，可从表中看出，流速的变化对绳索伸长量的影响较小。表6为逆流下PLET实际安装位置与预计安装位置之间的偏移量，逆向流速对于偏移量影响较大，且随着流速增大，落点偏移量也逐渐增大。实际安装中，PLET应在规定位置下落并与其他水下结构物进行连接，过大的偏移量会影响后续安装工作的进行，在流速较大的情况下，PLET安装接近海床时，应及时调整其安装位置，保证安装准确性。

表5 不同逆流流速下缆索伸长量

表6 不同逆流流速下PLET落点偏移

4.3 不同深度下PLET安装仿真

PLET的安装深度对安装过程也有着重要影响，设定安装深度分别为200、300和400 m，其他条件相同。

图17、18分别是不同安装深度下缆索张力、管道张力时间历程，缆索张力及管道张力均随安装深度的增加而逐渐增大，这主要是由于安装深度增加，PLET下端连接管道长度变长，缆索需要承担的质量增加，所以管道及缆索张力变大，400 m安装深度时，缆索受到的张力约可达到1.0×106N。

图17 不同安装深度下缆索张力时间历程

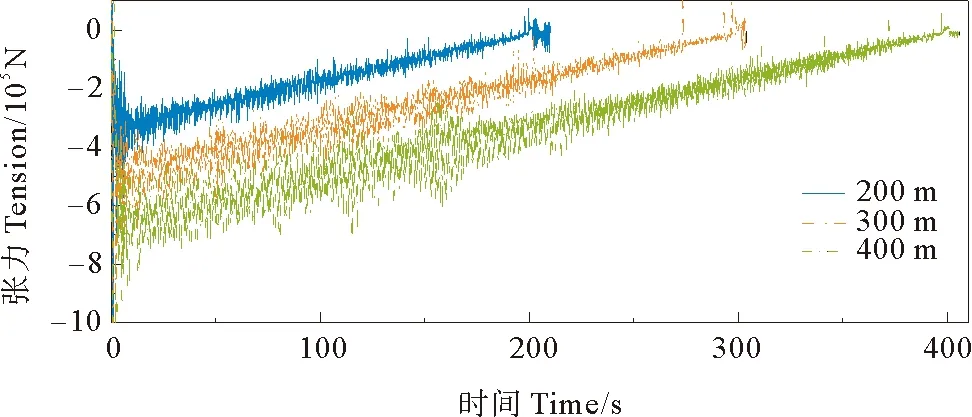
图18 不同安装深度管道张力时间历程

表7为不同安装深度下缆索伸长量，随着安装深度增加，缆索伸长量逐渐增大，并且接近线性增加，可得知：缆索的伸长量和安装深度呈线性关系。表8为不同的安装深度下PLET的落点偏移变化，安装深度的改变使水下流速分布情况产生了变化，随着深度的增加，落点位置的偏移逐渐增大，但不呈现线性变化，说明安装深度对安装位置会产生影响，但安装过程中，缆索拖拽力、缆索浮力与重力合力等因素共同作用导致结果不呈现线性。

表7 不同安装深度下缆索伸长量

表8 不同安装深度下PLET落点偏移

4.4 不同尺寸PLET安装仿真

更改PLET的规格尺寸，分别建立长×宽×高为5 m×3.5 m×2.2 m、6 m×4 m×2.5 m、7 m×5 m×2.7 m的PLET模型，对应质量分别为30、39、53 t，依据前文中建模理论进行建模，其余工况相同。

图19、20分别是不同PLET尺寸下的缆索张力、管道张力的时间历程，管道张力并未随PLET尺寸改变而变化，而缆索张力随PLET质量增大而增加，因而要对缆索的承载能力提出更高的要求。

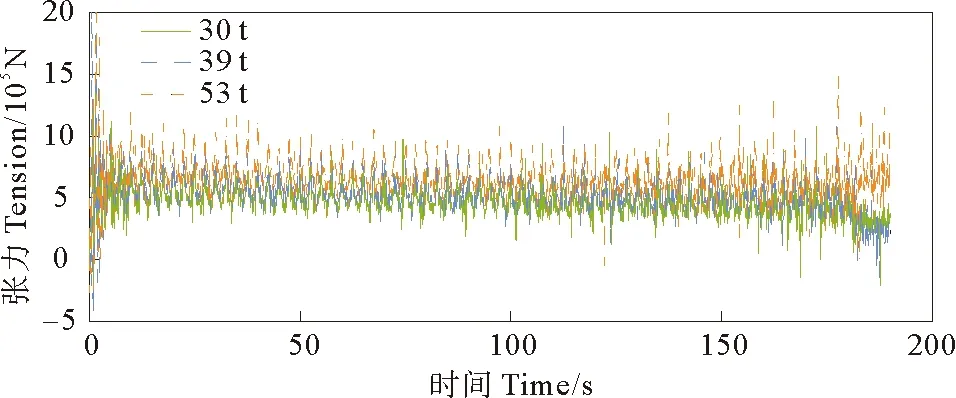
图19 不同PLET尺寸下缆索张力时间历程

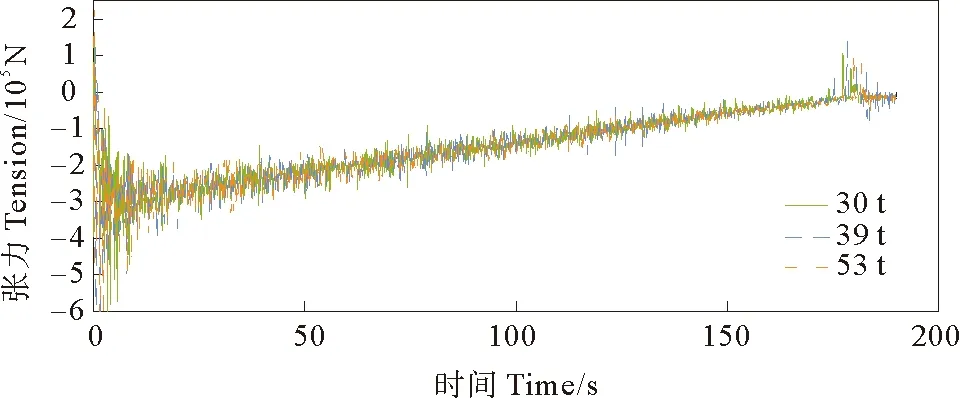
图20 不同PLET尺寸下管道张力时间历程

表9为进行不同PLET尺寸安装时缆索的伸长量，随着PLET质量的增加，缆索的伸长量逐渐增大，并且与PLET质量的增加接近呈线性增长关系。表10为不同PLET质量下的落点偏移，从表中可以看出，随着PLET质量的增加，落点的偏移量也逐渐增大。

表9 不同PLET尺寸下缆索伸长量

表10 不同PLET尺寸下落点偏移

5 结论

本文采用多体动力学方法对PLET布放过程进行研究，考虑了水深、流速、PLET尺寸等因素对缆索张力、管道张力、缆索伸长量及落点偏移的影响，建立了PLET布放过程，并对其进行了仿真研究，综合研究结果可得到以下结论：

(1)缆索张力主要受到安装水深以及PLET尺寸变化的影响，随着安装水深增大，铺设安装法所携带的管道质量增加，缆索所受张力增大。

(2)绳索的伸长量与PLET质量以及安装深度呈现近似线性的关系，随着PLET质量的增大以及安装深度的增加，绳索的伸长量逐渐增长。

(3)PLET的落点偏移量与流速、安装深度以及PLET质量的变化均有关，安装深度对其影响较小，随深度增加，偏移量增大，PLET远离安装位置；当正向流速增大时，PLET接近既定安装位置，但在实际安装时，流速的增大可能会导致安装船定位出现问题，所以在实际安装中，应在合适的海况下进行安装；当逆向流速增大时，PLET远离既定安装位置，且随着流速增大，落点偏移量也逐渐增大。当PLET质量逐渐增大时，降落至海床上的位置偏移量也越大，因此在安装中，应将PLET尺寸变化对于安装位置的偏移量进行提前考虑。