领航主机约束化的多四旋翼无人机编队航迹优化方法*

张利民 李 茜 柴旭朝 路向阳 刘若阳

1. 中原工学院电子信息学院，郑州 451191 2. 天津工业大学机械工程学院，天津 300387

0 引言

四旋翼无人机由于其机械结构简单、操控灵活方便等优点，近年受到了很多学者的关注[1-3]，四旋翼无人机多机协同航路规划是多架无人机协同作战任务规划系统中的关键技术，近年来有很多相关研究成果，比如，莫宏伟等[4]在蚁群算法改进的基础上，提出了变主方向搜索策略和简化的四旋翼无人机航迹策略；Chen等[5]针对多四旋翼无人机协同装配任务中的轨迹优化问题，提出了一种基于离线路径规划过程和在线轨迹规划过程的分层优化策略；Zhang等[6]提出了一种基于优先级的RRT算法，该算法为每个具有避障功能的四旋翼机生成一条在线全局路径，在障碍物密集的环境中实现多个四旋翼自主导航的分散运动规划；Iswanto等[7]结合模糊逻辑算法和单元分解算法，使四旋翼能够通过寻找最短路径快速移动到目标位置；Turpin等[8]控制一组微型四旋翼飞行器在三维环境中快速移动，同时保持紧密编队。

但目前的文献中少有对三维空间有约束情况下，利用四旋翼无人机编队队形信息的航迹优化研究。本文针对此问题，首先，建立四旋翼无人机动力学模型，分析其飞行过程中的约束条件，分析领航主机的约束问题，然后将跟随四旋翼无人机的约束转换为领航主机的约束，将多机的航迹优化问题转换为领航主机的单机三维空间航迹优化，并利用Gauss伪谱法(Gauss pseudo spectrum method，GPM)对领航主机进行单机航迹优化。

1 多四旋翼无人机编队约束分析

1.1 单四旋翼无人机的非线性模型

本文采用+字型四旋翼飞无人机，其结构简图如图1所示[4]。

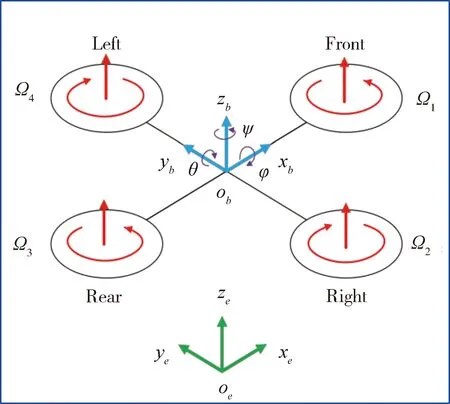
图1 四旋翼无人机结构示意图

四旋翼无人机的非线性模型[5-6]为：

(1)

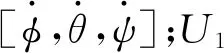
本文采用一致性理论定义各四旋翼无人机之间的队形保持问题，将编队系统转化为网络拓扑结构，通过一致性算法使得无人机的状态信息与期望信息保持一致，从而实现多无人机自主编队运动控制，本文对一致性控制不做研究。

1.2 领航四旋翼无人机约束条件分析

1)初始约束

四旋翼无人机在起始点t=0时需满足的初始位置和姿态约束，即：

(2)

2)终端约束

四旋翼无人机在到达目标点时需满足的终端位置和终端姿态约束为：

(3)

3)最小转弯半径

四旋翼无人机的自身特性决定了在需要拐弯时拐弯半径的最小值，另外，较大的转弯半径还够避免四旋翼无人机编队在改变队形时相互碰撞。一般情况下此半径大小需满足如下要求：

(4)

式中：V1为领航四旋翼无人机速度，R1为领航无人机转弯半径，g为重力加速度，n1max为领航无人机最大法向过载。

4)控制约束

Uimin≤Ui≤Uimax,i=1,2,3,4

(5)

5)最低飞行高度

四旋翼无人机一般在飞行过程中会遇到较高的地形或者敌方火力范围，因此在进行路径规划时要设定四旋翼无人机实时飞行的最低高度，确保所有的无人机在安全高度以上飞行。

z1(t)≥hmin(t),hmin(t)>0

(6)

其中：z1(t)为编队中领航无人机的实时飞行高度，hmin(t)为根据地形等数据得到的实时最低飞行高度要求。

6)水平方向约束

如果四旋翼无人机在一定的高度飞行时，可以在水平方向上要求其距离障碍物的外围轮廓保持一段安全距离，防止无人机因为惯性或者机动性不足而与障碍物发生碰撞，另外还可以利用障碍物的阻挡减小被敌方侦查到的概率。本文均以圆盘表示在一定飞行高度上对应的水平障碍物约束：

(x1(t)-xj)2+(y1(t)-yj)2>Rj,j=1,2,…，m

(7)

式中：(x1(t)，y1(t))表示领航无人机的实时位置，(xj,yj)和Rj分别表示第j个禁飞区圆盘的圆心和半径，m表示禁飞区总数。

1.3 跟随四旋翼无人机约束转换

在本文研究的多无人机编队航迹优化中，我们将跟随四旋翼无人机(从机)特性作为领航主机存在的约束条件，其转换为约束的处理如下：

1)从机位置约束转换：按照从机和领航主机在编队中的位置信息，可得到从机在惯性坐标系下的位置表示：

(8)

其中：(xi(t),yi(t),zi(t))为第i个从机的实时位置， (x1(t),y1(t),z1(t))为领航主机的实时位置，(xi1,yi1,zi1)为第i个从机和领航主机之间在队形中的相对位置，为已知值，从其表达式可以看出，对从机的位置约束处理时，可以将其变换为对领航主机的位置约束，于是，进一步，对于从机的最低飞行高度和水平方向的约束，我们可以做下面的分析。

2)从机最低飞行高度约束转换：

当从机飞行时要求的最低飞行高度约束为zi(t)=z1(t)-zi1≥himin(t)时，其中himin(t)>0，我们可以将其转换为领航主机的飞行高度约束，即

z1(t)≥hmin(t)+zi1

(9)

3) 从机水平方向约束转换：

和高度约束转换方法一样，如果我们要求从机在水平方向上距离障碍物某个点的距离要求(xi(t)-xj)2+(yi(t)-yj)2>Rj,j=1,2,…,m，其中Rj表示从机i距离第j个障碍物表面的最近距离，则我们可以将其转换为领航主机的水平方向约束，即

(x1(t)-xi1-xj)2+(y1(t)-yi1-yj)2>Rj

(10)

4)最小转弯半径

和领航无人机一样，从机的转弯半径大小也需满足如下要求：

(11)

(12)

于是可得从机与主机之间的速度关系：

(13)

式(11)左边可变为，

(14)

如果假设四旋翼无人机编队在转弯时，转弯中心的相对领航主机的位置坐标为(0, 0, 0)，则有：

(15)

即式(11)可变为：

(16)

这样，从机的最小转弯半径可转换为领航主机的最小转弯半径、速度和位置相关约束。

1.4 性能指标函数

本文采用编队能耗最小作为性能指标，即

(17)

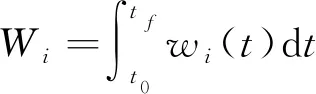
2 基于GPM的四旋翼编队航迹优化

2.1 Gauss伪谱法原理[9-11]

1)时域变换

采用Gauss伪谱法时，需要将时间区间[t0,tf]转换为[-1,1]，即

(18)

2)状态变量与控制变量的近似

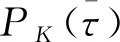
(19)

其中：

(20)

(21)

令式(19)中节点处的近似状态值和实际状态值相等，得Xi=X(τi)=x(τi)。

对于控制变量采用同样的方法离散，有

u(τk)=U(τk),k=1,…,K

(22)

即:

(23)

3)动力学微分方程约束

对式(19)求节点上微分：

(24)

其中：微分矩阵可以离线确定，即:

(25)

从而动力学微分方程约束转换为代数约束:

(26)

其中：k= 1,…,K。

4)终端状态约束的处理

状态变量在终端时刻节点需要单独处理，终端状态应满足如下动力学方程约束:

(27)

将式(27) Gauss积分公式近似得:

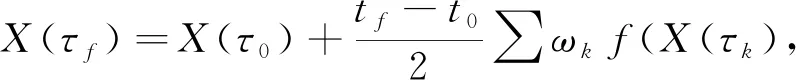
(28)

5)性能指标函数的近似

将性能指标函数中的积分项采用Gauss积分公式近似得：

(29)

6)Gauss伪谱法的一般描述

根据上述数学变换，Gauss伪谱法求解最优控制问题的原理可以描述为：求离散节点上的状态变量Xi，i=0,…,K和控制变量Uk，k= 1,…,K，以及初末时刻t0和tf，使得性能指标式(29)最小，并满足终端状态约束式(26)，以及原最优控制问题的边界条件式(27)，以及原最优控制问题的边界条件

φ(X0,t0,Xf,tf)=0

(30)

C(Xk,Uk,τk;t0,tf)≤0,k=1,…，K

(31)

从而将原最优控制问题转化成非线性规划问题(NLP)，即:

(32)

其中:y为设计变量，包含控制变量、状态变量和两个端点时间。目前已有很多种有效方法求解非线性规划问题，其中序列二次规划算法(SQP)以其局部超一次收敛性、整体收敛性得到广泛应用，Gauss伪谱法采用SQP算法处理转换而来的NLP问题。

2.2 四旋翼无人机编队最优控制问题转换分析

从四旋翼无人机的模型可以看出，四旋翼无人机的航迹优化属于强非线性的最优控制问题，其求解比较复杂，本文借鉴Gauss伪谱法GPM思想，将最优控制问题转化为一系列具有代数约束的参数优化问题，即非线性规划问题。

经过本文的分析，四旋翼无人机编队最优控制问题的最优航迹规划问题可描述为：在满足动力学微分方程约束式(1)、领航主机的边界条件式(2)和(3)、最小转弯半径约束式(4)、控制约束式(5)、最低飞行高度约束式(6)、水平方向约束下式(7)和跟随四旋翼无人机转换为领航主机的约束式(8)((10)和(12)，寻求最优控制量u(t)，使性能指标式(17)最小。

3 仿真校验

实验针对6架四旋翼无人机组成的多机编队，起飞时以等边三角形编队，编队保持策略是领航跟随法。规定领航四旋翼无人机要完成的任务是：在指定出发点(x0,y0,z0)=(2,1,3)m，以初始速度矢量(vx0,vy0,vz0)=(2,2,0)m/s，给定的初始姿态角(ψ0,θ0,φ0)=(45°,0°,0°)初始出发，穿过分布了多个山峰的非平地区域，以指定的速度矢量(vxf,vyf,vzf)=(0,0,0)m/s、(ψf,θf,φf)=(30°,0°,0°)姿态角，在规定的时间t=330s时从较高的高度到达目的地点(1200,1000,2)m。5架跟随无人机的起飞位置分别为(0,0,3)m，(0,3,3)m，(1,0.5,3)m，(0,0.5,3)m，(1,1.5,3)m，起飞速度矢量、姿态角、末端速度矢量和姿态角与领航无人机相同。地形约束模型采用由式(33)生成的地面高度和式(34)生成的山峰地形数据[12-13]。

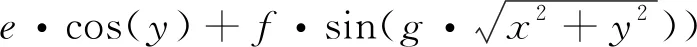
(33)

(34)

实验中使用的四旋翼无人机其他相关参数如表1和式(35)所示。

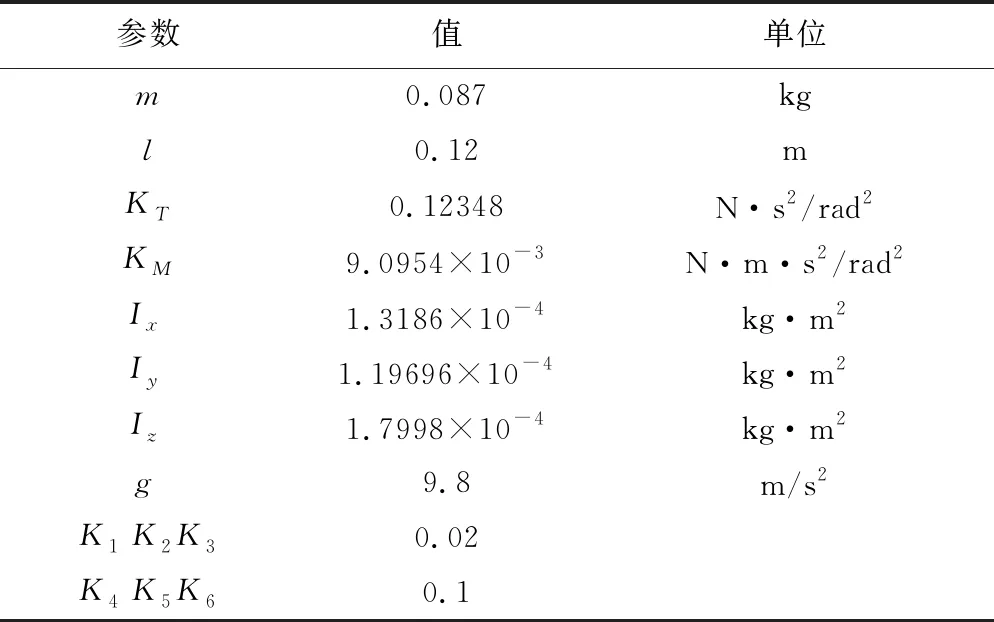
表1 仿真参数设置

(35)

在采用领航跟随策略的无人机编队中，首先要为领航者指定参考航迹，使用本文方法生成了领航者无人机的参考航迹，用GPM生成的航迹以节点形式给出，通过自适应选点的B样条平滑策略平滑处理，并加以最大值约束。其结果如图2所示。

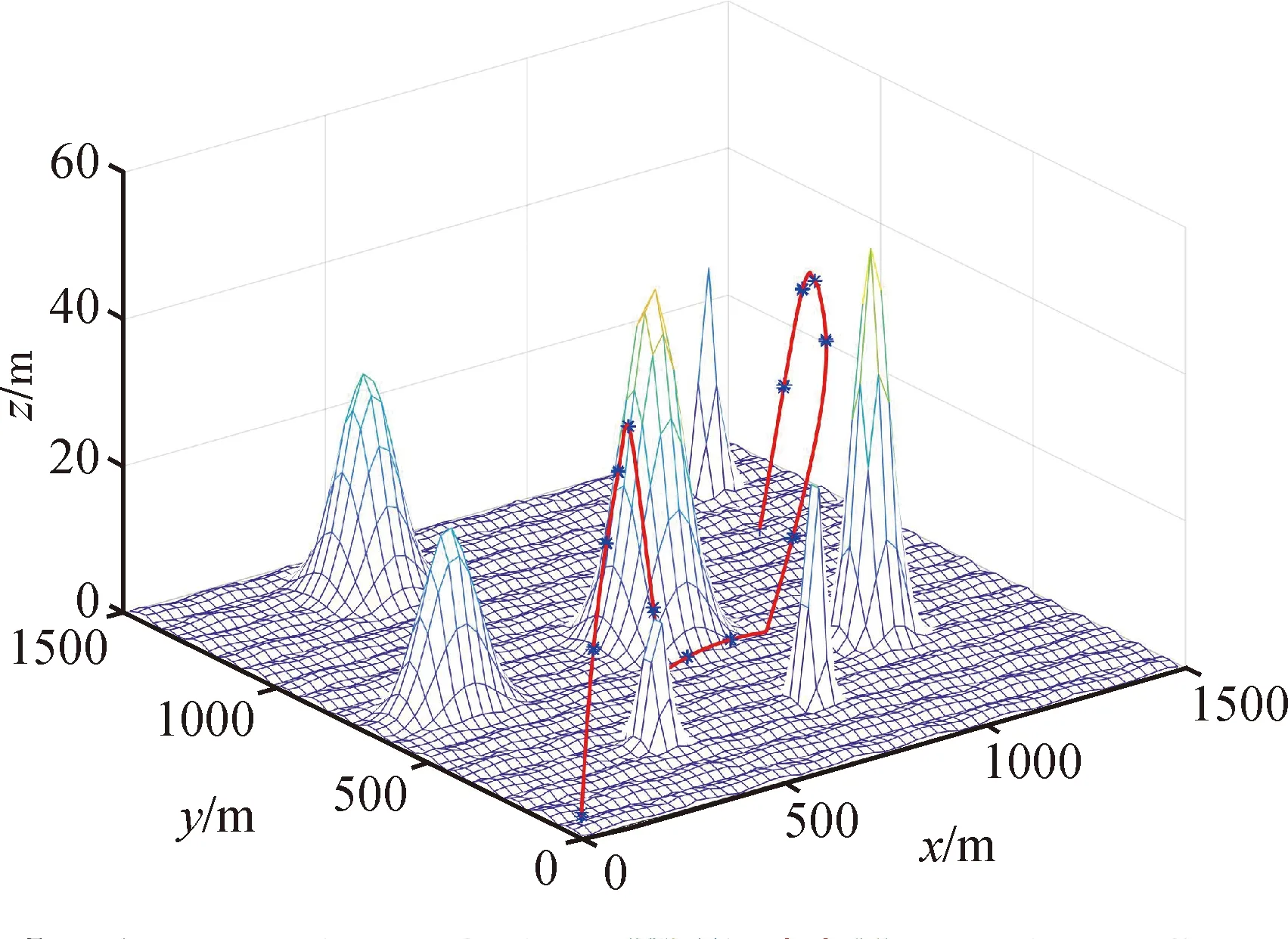
图2 生成的领航者航迹

图2展示了领航者无人机在分布了多个障碍物环境下的航迹，可以看出该航迹与所有障碍物都未发生碰撞，并能从起点到达指定终点。图中实心点代表无人机编队示意图。从图2可以看出规划的飞行路径平滑，均满足约束条件。在飞行末端无人机编队从较高位置逐渐降落在指定高度2m。在飞行过程中，飞行路径先后经过上升-下降-上升-下降4个过程，这个过程为消耗多余时间而进行的飞行。

领航主机的航向角、俯仰角、横滚角的变化曲线分别如图3～5所示。

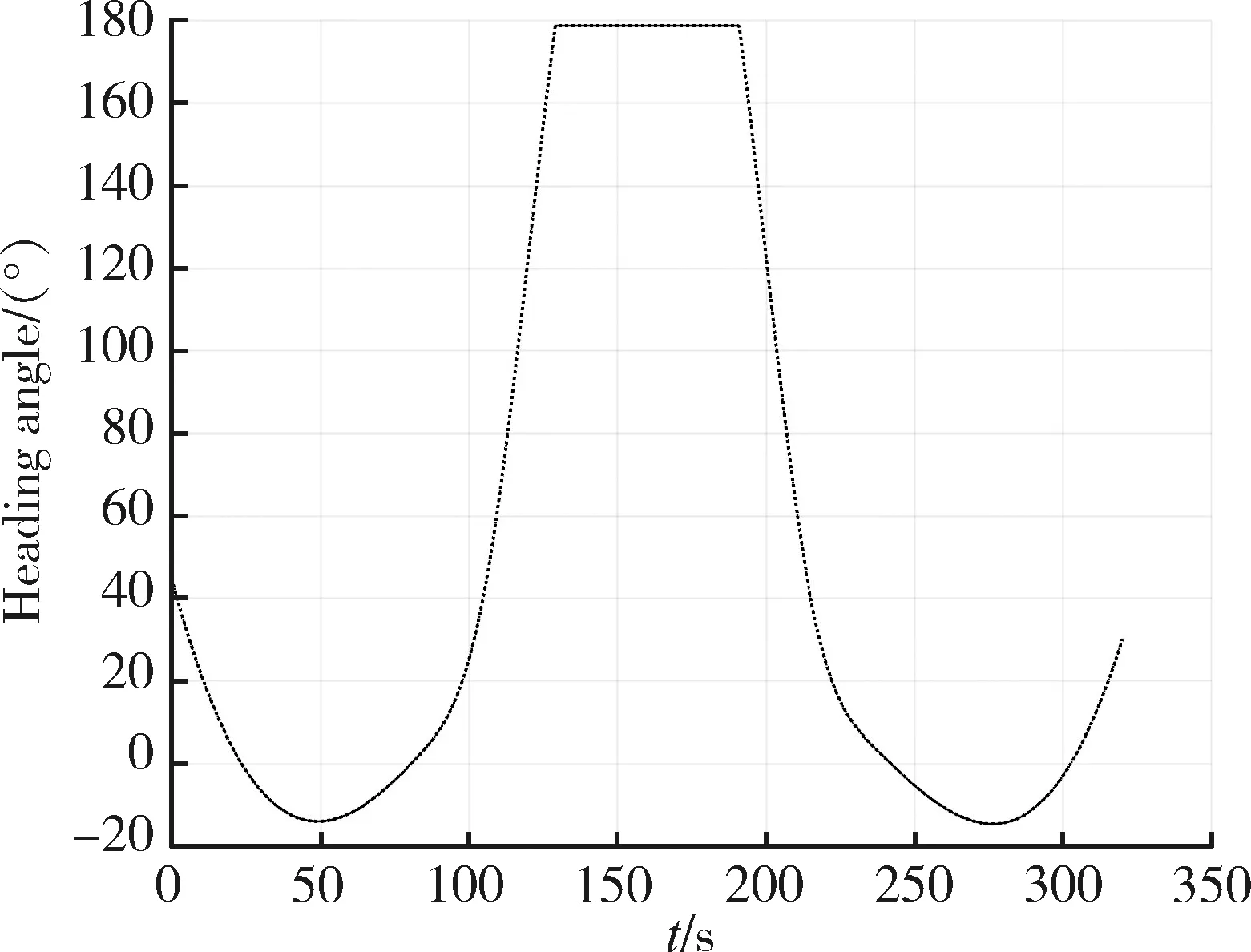
图3 领航主机航向角

从图3可以看出，领航主机经过4次航向变化，这部分对应的正是穿越山峰区域的时间，通过航向的变化可以在山峰直接穿越。中间有一段保持航向不变的飞行时间，此段时间为山谷间的平地飞行(或地面高度值不大)。从图4可以看出，领航主机经过2次爬升和2次降落过程。爬升过程均为翻越较低山峰准备，第1次降落过程为越过山峰后的过程，第2次降落为到达目的地后，根据要求从较高的高度逐渐降低到目标高度的过程。从图5可以看出，领航主机在飞行过程中通过小角度翻滚带领从机规避障碍物或地形，最终到达目的地时回到无翻滚状态。

图4 领航主机俯仰角

图5 领航主机横滚角

图6～7分别为控制量U1、U2、U3和U4的变化曲线图。

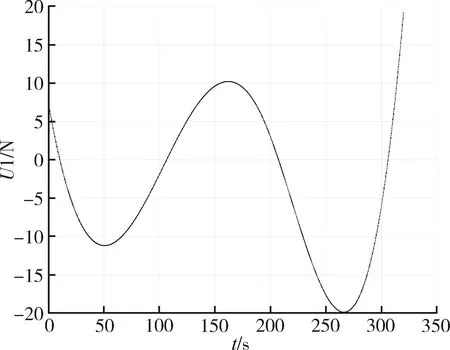
图6 领航主机控制量U1

从图6可以看出，通过U1改变3个空间方向的速度，实现无人机轨迹的变化，达到领航主机规避障碍物和消耗多余时间的要求。从图7可以看出，三个姿态角在飞行过程中微小的变化，是为了改变领航主机的飞行方向和姿态稳定性或者规避障碍物。

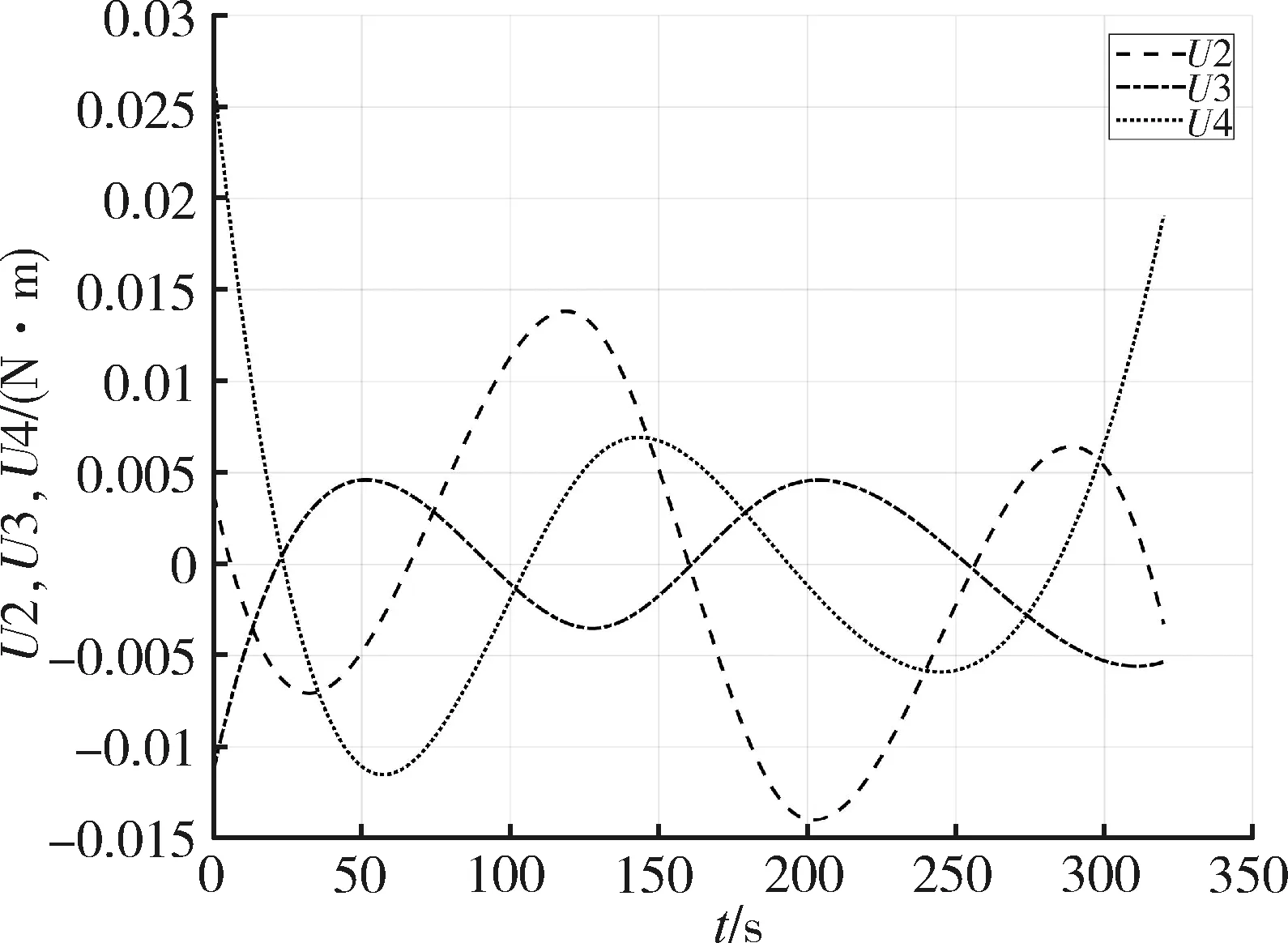
图7 领航主机控制量U2、U3和U4

4 结论

本文对四旋翼无人机编队问题进行了研究，首先采用了领航-跟随法的策略，并基于一致性理论将编队系统转化为网络拓扑结构，将编队看成一个虚拟刚体。在此基础上，首先分析了领航四旋翼无人机自身的一些约束条件，然后将编队中的跟随无人机信息进行分析，转换为领航主机的约束，将编队问题单机化，最后，给出了四旋翼无人机编队航迹优化问题的分析，提出基于Gauss伪谱法将航迹优化的最优控制问题全部转换到非线性规划的求解框架之中。最后的仿真结果表明了方法的有效性。