高速航行体齐射出水过程的空化与运动特性研究
2023-03-13周东辉贾会霞施红辉王焯锴
周东辉,贾会霞,施红辉,王焯锴
(1.浙江工业职业技术学院,绍兴 312000;2.西北工业大学 宁波研究院,宁波 315100;3.浙江理工大学 机械与自动控制学院,杭州 310018)
0 引言
从水下发射超空泡射弹攻击水面目标或者低空飞行目标,可提高武器发射的隐蔽性,增强其作战效果。例如挪威 DSG 公司研制的多环境枪弹[1],可实现水下5 m 深度发射,打击1 000 m 飞行高度的直升机。德国研制的反气垫船超空泡射弹,可预先在水下将射弹垂直布置,当目标出现后在不到1 s 时间内完成攻击任务[2]。在实际应用中,为了提高射弹的命中概率和毁伤效果,往往需要采用齐射方式,即以一定发射空间间距、在极短时间间隔内连续发射多发射弹。齐射出水过程中,不仅会出现空化、湍动、穿越自由面等复杂的三相耦合流动现象,还存在多弹体超空泡流场的相互扰动,导致射弹的超空泡流动和运动特性非常复杂。因此,开展相关的研究具有重要的学术研究和工程应用价值。
针对带空泡航行体的出水问题,其中出水空泡形成、发展、溃灭以及影响因素分析等方面一直是研究重点,这主要是由于空泡的形态、溃灭关系到航行体的受力及冲击载荷,进而影响航行体出水过程的弹道稳定性和结构安全。在国外,Waugh 等[3]通过实验研究了发射角度和空泡对导弹出水姿态的扰动影响,给出了出水空泡的形态。Nguyen 等[4]利用数值模拟方法研究了射弹匀速出水过程的超空泡流动,给出了射弹出水过程的阻力变化和超空泡形态。Logvinovich等[5]提出了空泡截面独立膨胀原理,给出了计算超空泡特征直径和特征长度的半经验公式。Savchenko等[6]修正了Logvinovich 提出的计算超空泡轮廓的半经验公式。在国内,褚学森等[7]利用均质多相流方法对圆柱体垂直出水进行了数值模拟,研究发现空泡在圆柱体的肩部和尾部形成,在穿越自由面的过程中溃灭。颜开等[8]对空化器朝水面高速运动产生的非定常空泡进行了理论研究,计算了空化器出水后空泡从脱落、收缩到溃灭的时间。魏海鹏等[9]分析了空化数及非凝结性气体含量对潜射导弹空化流动的影响。施红辉等[10-12]对射弹高速出水的超空泡流动进行了实验和数值模拟研究,获得了出水超空泡的演化过程,分析了超空泡发展对射弹出水姿态的影响以及射弹头部形状对射弹运动、超空泡形态等的影响。王一伟等[13-14]采用实验和数值模拟相结合的方法研究了射弹垂直出水过程的非定常空化流动,给出了出水空泡的演化和射弹表面压力分布特征,揭示了空泡发生溃灭的机制。付国强等[15]对细长体垂直出水过程的空化流动进行了实验研究,分析了水深和发射速度对空泡发展的影响。陈瑛等[16]采用大涡模拟的方法对潜射航行体出水过程的空化流动进行了数值模拟,给出了出水空泡的演化过程、湍流结构和压力特征,讨论了潜射深度、发射速度、迎角的影响。Chen 等[17]利用自行设计的水下发射平台开展了射弹垂直出水实验,研究了射弹头部形状和发射速度对出水空泡演化和射弹运动的影响,分析了空化数、再进入射流与空泡稳定性之间的关系。
针对多个航行体出水的研究,Mnasri 等[18]建立双圆柱体低速并联出水的二维数值模拟,分析了流场的相互扰动。卢佳兴等[19]开展了发射速度为15 m/s的两发回转体齐射出水实验,获得了齐射过程中回转体的空泡演化特性和运动特性。施红辉等[20]进行了两发超空泡射弹连续出水过程的数值模拟,分析了出水过程超空泡流场的干扰规律以及超空泡演化过程对射弹运动的影响。毕凤阳等[21]建立了多细长体水下齐射多相流动与多体运动耦合数值模拟的计算模型,研究了细长体筒中段及离筒初期的流动、运动及干扰特性。Xu 等[22]进行了两发射弹齐射出筒的六自由度数值模拟,研究了尾流的演化及其与射弹的相互作用。Gao 等[23]基于VOF 方法研究了射弹水下齐射过程中的流动干扰特性,获得了射弹表面的压力分布、水动力特性、弹道特性以及俯仰角的变化,由于射弹的发射速度较低,不考虑自然空化作用。
综上所述,目前的研究集中在航行体单独出水的空泡演化、流体动力及运动特性,对多发航行体齐射出水的研究较少,仍处于探索阶段,而且已有齐射出水的研究涉及自然空化作用的较少。因此,本文基于VOF 多相流模型,通过重叠网格技术开展了双发射弹齐射出水问题的数值模拟研究,获得了齐射出水过程的超空泡演化特性、射弹的运动轨迹、偏转角变化、速度衰减曲线和阻力特性,分析了超空泡流场的干扰机理以及发射时差的影响。研究结果可为水下多弹齐射安全性分析和方案设计提供相关的参考。
1 数学模型及数值方法
1.1 控制方程
采用均质多相流模型来处理射弹出水过程诱导的多相流动,即将水、空气、水蒸气三相当作单一介质的混合相,混合相的密度由各相的密度和体积率共同决定,各相之间不存在速度滑移,并且具有相同的压力场和速度场,流场计算时只对混合相求解N-S 方程和湍流方程。
混合相的连续性方程和动量方程分别为:
式中:ρm为 混合相密度;xi、xj为笛卡尔坐标分量;ui、uj分别为笛卡尔坐标系中的速度分量;p为压力;µm为混合相动力黏度;gi为重力加速度的分量。
混合相密度的表达式为:
式中:αv、αg分 别为水蒸气、空气的体积分数;ρv、ρl、ρg分别为水蒸气、水和空气的密度。
混合相的动力黏度的表达式为:
式中:µv、µl、µg分别为水蒸气、水和空气的动力黏度。
采用SSTk-ω湍流模型[24]对雷诺平均方程提供湍流封闭,该模型考虑了湍流剪切应力传输,综合了k-ε模型在外部区域模拟和标准的k-ω湍流模型在近壁计算的优点,能够精确模拟逆压梯度下出现的流动分离现象。
涡黏性系数 µt的表达式为:
湍动能k和比耗散率 ω的输运方程如下:
式中:σk、σω是 湍动能k、比耗散率 ω的湍流普朗特数;Gk、Gω分别为湍动能、比耗散率产生项;Sk与Sω为自定义项;Yk、Yω分别为湍动能、比耗散率的发散相;Dω为正交发散项。
空气和水蒸气相的体积分数的输运方程为:
空化问题的求解采用基于Rayleigh-Plesset 气泡方程建立的Schnerr-Sauer 空化模型:
式中:RB为 气核的半径;pv为水的饱和蒸气压力;n0为单位液体体积空泡个数,取值为1×1011。
1.2 6DOF 刚体运动模型
射弹在流场的运动通过6DOF 刚体运动模型[25]来求解。射弹运动可分为质心的平动和绕质心的转动,在惯性参考坐标系下建立射弹的平移运动控制方程:
式中:VG为射弹质心的平移速度矢量;m为射弹的质量;FG是射弹受到的外力矢量。
射弹的转动在刚体坐标下的控制方程为:
式中:ωp为射弹角速度矢量;I为射弹的惯性张量;M为射弹外力矩矢量。
1.3 计算模型、边界条件及数值方法
本文数值计算采用的射弹模型为参考文献[10]的射弹模型,射弹为截锥型回转体,由头部锥台段和圆柱段组成,弹体总长L=48 mm,头部空化器直径D0=3 mm,锥台段L0=18 mm,如图1 所示,质量m为2.98 g。
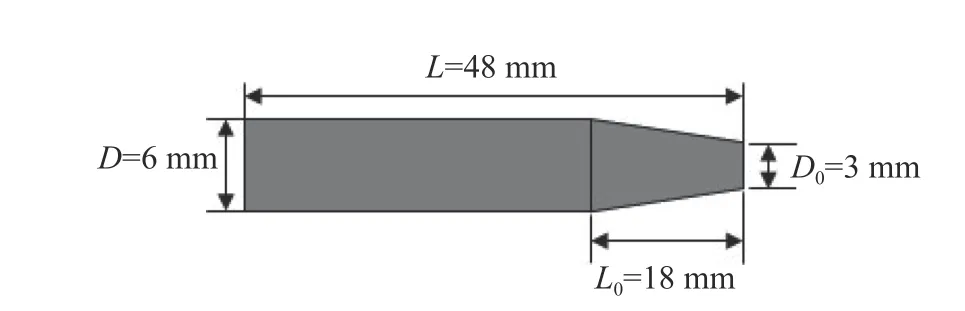
图1 射弹的几何模型Fig.1 Geometric model of projectile
计算域和边界条件如图2 所示,计算域长35D、宽20D、高130D,空气域高度为50D,水域高度为80D,首发射弹和次发射弹的质心距离自由液面的高度h均为71.2D,两射弹中轴线之间的距离为4D。计算域底部为压力入口,压强为105 704 Pa,计算域顶部为压力出口,压强为标准大气压,4 个侧面均为压力出口,压强依据水深环境指定,其压力梯度分布由用户自定义场函数定义。首发射弹和次发射弹的表面均设定为无滑移壁面条件。定义处于两射弹的中间区域为射弹的内侧,其余为射弹的外侧。
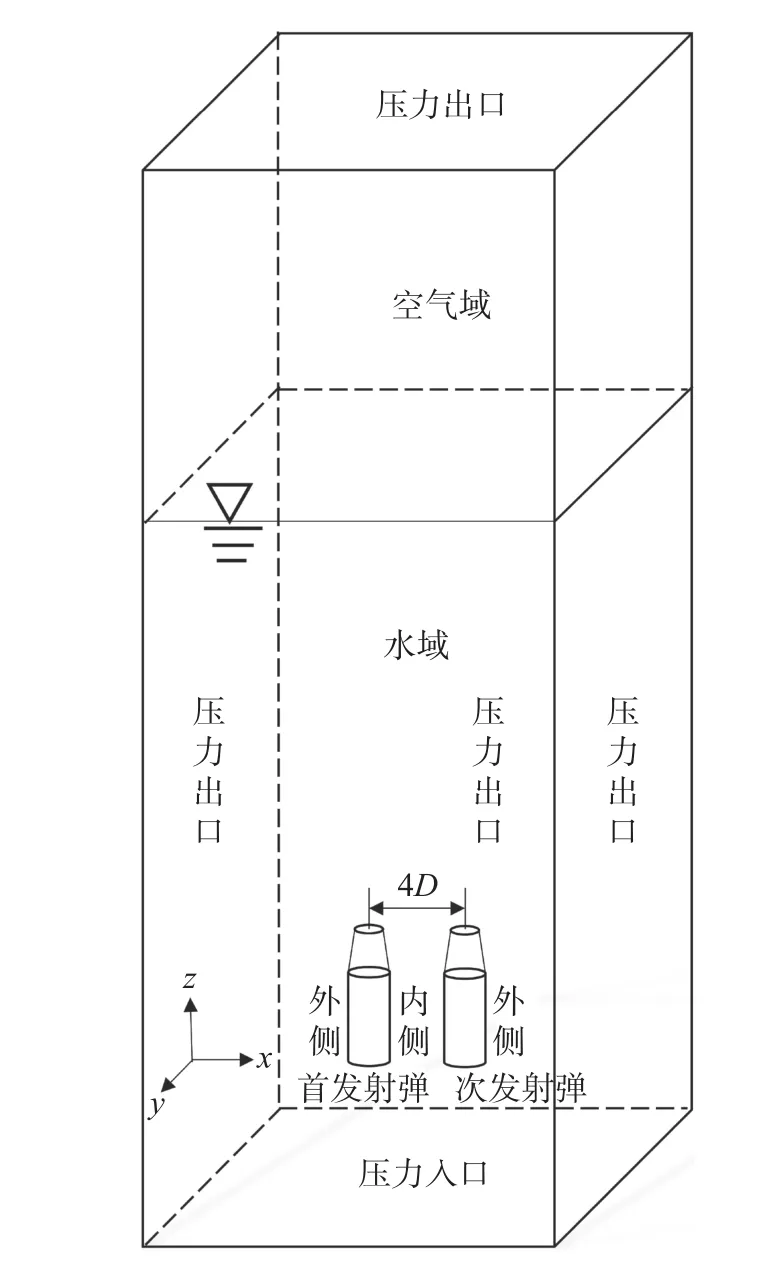
图2 计算域及边界条件设置Fig.2 Computational domain and boundary condition setting
两发射弹齐射出水过程中,首发射弹和次发射弹的发射时间间隔为发射时差 Δt。当 Δt=0 时,被称为同步发射;当 Δt≠0 时,被称为异步发射,异步发射过程中首发射弹先发射,随后次发射弹发射。在数值模拟中通过UDF 控制次发射弹在水下运动的起始时间从而实现两发射弹以不同发射时差出水,出水过程中,首发射弹和次发射弹的初速度均为150 m/s。
计算域网格划分使用重叠网格技术,该技术对计算流场中多物体运动比较有效。计算区域分为背景网格区域和子网格区域,整个流场为背景网格区域,由于首发射弹和次发射弹分别独立运动,因此需要划分两个子网格区域,两个子网格区域大小相同,均为包裹射弹的圆柱,其长度为10D,直径为3D。图3 为计算域的网格划分示意图,均采用结构化网格进行划分,背景区域中对航行体运动区域和自由液面附近的网格进行局部加密,以便精确捕捉超空泡界面和自由液面的变形,子区域中对射弹壁面附近的网格进行局部加密。计算中,设置子网格1 计算域与首发射弹同步运动以及子网格2 计算域与次发射弹同步运动,然后结合 6DOF 算法可以实现两个射弹各自独立运动的六自由度运动求解。计算模型中压力与速度耦合的求解采用Coupled 算法,压力场和空间离散采用PRESTO!格式,数值计算中时间步长选择为1×10-6s。
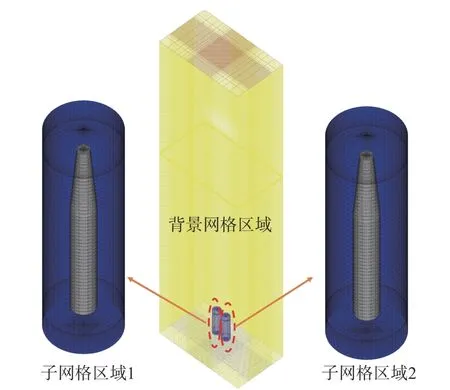
图3 网格划分示意图Fig.3 Schematic of computational domain grids
1.4 无量纲数
对文中的物理量进行无量纲化:
式中:t为时间;v0为 射弹的初速度;Δt为两发射弹的发射时差;vz为射弹的竖直速度;z为射弹质心的竖直位移;x为射弹质心的水平位移。
定义无量纲超空泡半径、无量纲位置:
式中:r为在zs位置处的超空泡轮廓半径,设定空泡外侧轮廓到中轴线距离为负,空泡内侧轮廓到中轴线距离为正。
式中:p0为标准大气压;Fz为射弹在z轴方向受到的阻力;A0为空化器的沾湿面积,这里取射弹头部的横截面积。
2 数值方法验证
先进行网格无关性验证,针对发射时差 Δ=0 的两发射弹齐射出水采用了3 种不同数量的网格进行数值模拟,网格数分别为157 万(粗糙尺度网格)、274 万(中等尺度网格)、362 万(精细尺度网格),不同网格尺度下首发射弹的无量纲竖直速度的变化如图4 所示。从图中可以看出,随着网格密度的增加,中等尺度网格和精细网格计算所得的结果基本一致,综合考虑计算精度和计算效率,故选取了中等尺度网格开展数值计算。
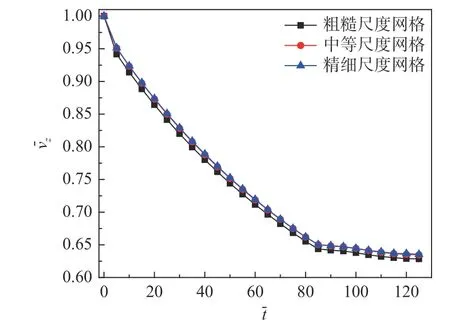
图4 不同网格数量下无量纲竖直速度衰减曲线Fig.4 Dimensionless vertical velocity attenuations of different grid numbers
采用文献中[10]中的超空泡射弹出水的实验数据进行数值方法的有效性验证,实验中的射弹模型与本文数值计算采用的射弹模型相同(见图1),实验中射弹的出水初速度为98 m/s。图5 表示的是超空泡射弹出水过程的实验和数值模拟结果对比,图中相邻图片的无量纲时间间隔为24.5,通过对比可以发现,整体上数值模拟结果和实验结果吻合度较好,但数值模拟中水在射弹尾部两侧的附着现象与实验结果不太一致,其原因为射弹尾部两侧的水破碎成液滴,继而受到重力作用下降,而数值模拟中对此破碎过程难以准确模拟。另外在数值模拟中尾空泡的长度要长于实验观测,这是由于超空泡尾部闭合区域是充满蒸气、液滴和旋涡的多相流湍流区,数值模拟很难精确模拟超空泡尾部滞止及溃灭。为了进一步验证数值模拟方法的准确性,将射弹的无量纲竖直位移的数值结果与实验数据进行对比,如图6 所示。从图中可以看出射弹无量纲竖直位移的数值结果与实验数据具有较好的一致性,其最大误差约为3.9%,误差结果在可接受的范围。因此,经过上述的比较,说明本文采用的数值模拟方法是有效的。

图5 超空泡射弹出水过程的实验[10]和数值模拟结果对比Fig.5 Comparison of the water-exit process between experimental and numerical simulation results
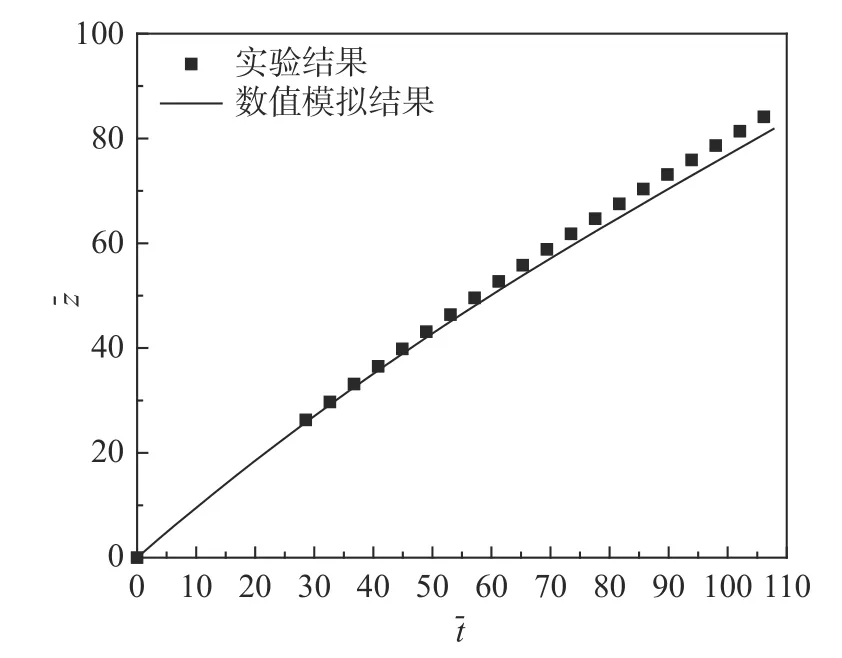
图6 无量纲竖直位移变化的实验和数值模拟结果对比Fig.6 Comparison of dimensionless vertical displacement between experimental and numerical simulation results
3 结果与讨论
3.1 空化流场特性分析
图7 给出了4 种发射无量纲时差条件下双发射弹齐射出水过程的水相图。为便于讨论,定义处于两射弹中间区域的超空泡壁面为超空泡内侧壁面,其余为超空泡外侧壁面。齐射过程中,两发射弹都经历了超空泡的生成、发展、溃灭,在出水阶段,伴随着自由面的抬升和隆起,剧烈喷溅出水花等现象。对于同步发射,两发射弹的超空泡内侧壁面同时扩张时,由于超空泡内侧壁面附近的流体形成了对流,抑制了超空泡向两射弹中间区域的扩张,而外侧壁面自由扩张,导致单个超空泡失去了对称性;随着时间的发展,两个超空泡在尾部区域相互靠拢,但两个超空泡在空间上呈现了良好的镜面对称特征。不同于同步发射的工况,Δ=25 的异步发射过程超空泡形态有较大差别,从图7(b)中可知,首发射弹先进入水中运动,其诱导的超空泡迅速扩张,空泡轮廓正常发展;随后次发射弹紧随而来,在次发射弹流场的干扰下,首发射弹超空泡尾部区域的内侧壁面发生收缩并且空泡尾部溃灭的速度加快,而次发射弹超空泡内侧壁面发生膨胀。结合图8,根据Logvinovich 的空泡截面独立扩张原理[5],空泡的每个横截面的膨胀扩张只取决于空泡外界和空泡内部的压差,以及头部空化器经过该截面时的速度、空化器的尺寸及阻力。对于本工况,影响空泡截面扩张的决定性因素是空泡外界和空泡内部的压差。射弹在水下高速运动,射弹头部区域生成高压区,诱导生成的超空泡内部为低压区,其值等于水的饱和蒸气压(约为3 540 Pa)。对于首发射弹超空泡,在次发射弹头部高压区持续压缩下,处于高压区附近的首发射弹空泡内侧壁面率先收缩;对于次发射弹超空泡,由于内侧区域的空泡内外压力差相对外侧较小,导致次发射弹空泡内侧壁面扩张的幅度更大。对于 Δ=50 和Δ=75,它们的空泡演化过程和 Δ=25相似,这里不再赘述。

图7 不同发射无量纲时差下射弹齐射出水的水相图Fig.7 Supercavity evolutions of two projectiles exiting water in underwater salvo for different launch dimensionless time intervals

图8 Δ =25 时,超空泡演化示意图Fig.8 Diagram of supercavity evolutions for Δ =25
图9 表示的是 Δ=75、次发射弹典型时刻的无量纲压力云图。结合图9(d)可以看出,首发射弹出水后剥离在自由面下的空泡发生收缩溃灭,在溃灭的过程中空泡上端和下端产生了局部高压,此时次发射弹处于该空泡的附近,引起次发射弹头部附近的压力场与空泡溃灭产生的局部高压发生耦合作用。在首发射弹脱体空泡溃灭造成的局部高压作用下,次发射弹超空泡在相同水深的空泡壁面率先发生收缩,最终出现了“颈缩”现象”,如图7(d)中=175 所示。
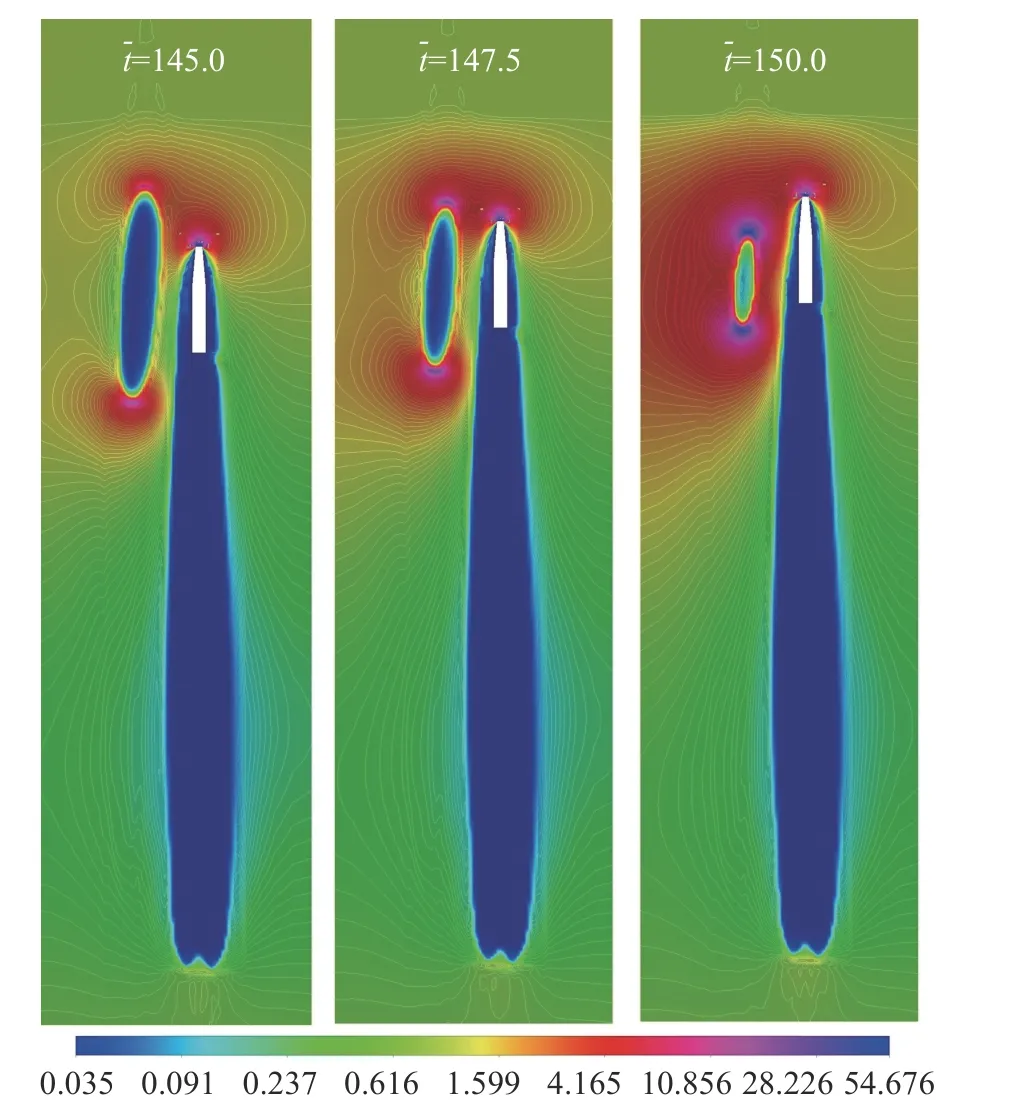
图9 Δ =75,次发射弹典型时刻的无量纲压力云图Fig.9 Dimensionless pressure distributions at typical time of the second projectile for Δ =75
由于射弹在水下高速航行时的空化数很小,超空泡的全局尺寸很大,但只有射弹附近的空泡形态对流体动力特性有影响。因此,本文选择超空泡前沿轮廓(2 倍弹长)作为研究对象。图10 给出了不同发射时差下射弹在特征位置处的前沿轮廓对比,其中图10(a)为首发射弹在无量纲竖直位移=61 时的超空泡前沿轮廓对比,图10(b)为次发射弹在=23 时的超空泡前沿轮廓对比。在图10(a)中,同步发射条件下的首发射弹超空泡外侧前沿轮廓曲率大于内侧的,而异步发射条件下的首发射弹的超空泡前沿轮廓对称性较好,这是由于同步发射时,超空泡的内侧受到相邻射弹的排挤作用,空泡内侧壁面的扩张受到抑制,而空泡外侧壁面自由扩张,异步发射时,首发射弹超空泡的前沿部分不受次发射弹流场的干扰,空泡前沿的外侧和内侧壁面均自由发展,超空泡前沿轮廓左右基本对称。从图10(b)中可知,对于异步发射,超空泡外侧前沿轮廓的曲率小于内侧前沿轮廓的曲率,其原因上文已给出分析,并且次发射弹超空泡内侧前沿轮廓曲率随着发射时差的增大而减小。
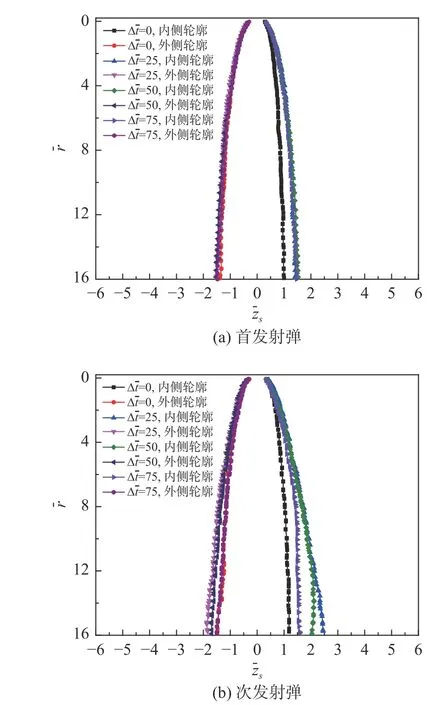
图10 特征位置处的射弹超空泡前沿轮廓对比Fig.10 Comparison of the front part of supercavity profiles at the feature position

图11 Δ =0,出水阶段特征位置的射弹表面无量纲压力分布及超空泡轮廓图Fig.11 Dimensionless pressure distributions on the projectile surface and supercavity profiles at the feature position of water exit stage for Δ =0
3.2 运动特性分析
图12 为出水过程射弹的运动轨迹。从图12(a)中可知,异步发射的3 种发射时差下,首发射弹的运动轨迹几乎为一条竖直线,这是由于异步发射时,次发射弹主要干扰的是首发射弹超空泡的尾部部分,对射弹附近的空泡形态几乎无影响,而决定射弹流体动力的是射弹附近的空泡形态,这也表明异步发射条件下次发射弹流场对首发射弹的运动基本无干扰。对于同步发射,首发射弹的质心先向内侧偏移,随后向外侧偏移,当完全出水后,首发射弹质心的轨迹基本为直线变化。由图12(b)可知,对于同步发射,次发射弹和首发射弹的运动具有对称性。对于异步发射,由于受到首发射弹超空泡流场的干扰,次发射弹在内外两侧压差作用下质心先向内侧偏移,在穿越自由面阶段有所波动。异步发射条件下,次发射弹质心的最大无量纲水平位移随发射时差的增大而减小。
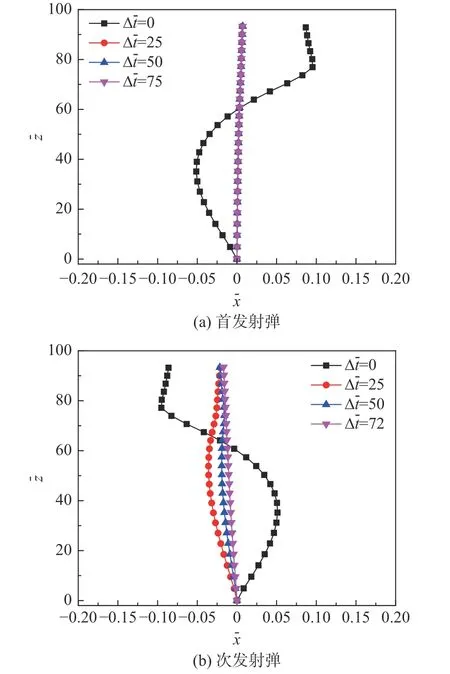
图12 出水过程射弹的运动轨迹Fig.12 Trajectories during the projectiles exiting water
图13 为不同发射无量纲时差下射弹偏转角随无量纲竖直位移的变化,定义偏转角θ为当前射弹轴线与竖直方向z轴的夹角,取射弹发生逆时针偏转时为正值。从图中可知,同步发射条件下,由于两发射弹头部附近区域均产生了高压区,压力场的作用下产生了方向相反的力矩,首发射弹逆时针偏转,次发射弹顺时针偏转,即两发射弹的运动向着两者头部远离、尾部靠近的方向偏转。此种工况下,首发射弹和次发射弹的偏转角大小随着无量纲竖直位移的增大而逐渐增大,最大值达到了3.1°;当射弹出水后,由于超空泡的不对称溃灭(图11 可知),使射弹产生了相反方向的俯仰力矩,其偏转角开始减小。对于异步发射,出水过程中首发射弹的偏转角基本为0°,而次发射弹由于受到首发射弹超空泡尾部低压流场的影响发生逆时针偏转,随着次发射弹向上运动距离逐渐增大,在出水后,其偏转角发生波动。次发射弹的最大偏转角随发射时差的增大而减小,当发射时差 Δ=75 时,次发射弹的偏转角几乎维持在0°附近。

图13 不同发射无量纲时差下射弹偏转角随无量纲竖直位移的变化Fig.13 Variations of deflection angles of projectiles with dimensionless vertical displacement for different launch dimensionless time intervals
图14 表示出水过程中射弹无量纲竖直速度衰减曲线。图14(b)中定义为当地无量纲时间,时间零点为次发射弹发射时刻。从图中可以看出,运动过程中4 种发射时差的首发射弹和次发射弹的无量纲竖直速度之间的差异较小。从放大图中可知,同步发射条件下首发射弹和次发射弹的无量纲竖直速度衰减略快,这是因为同步发射相对异步发射,首发射弹发生了较大偏转,阻力增加,产生了更大的能量损失,这表明同步发射会对超空泡射弹的减阻产生不利影响。
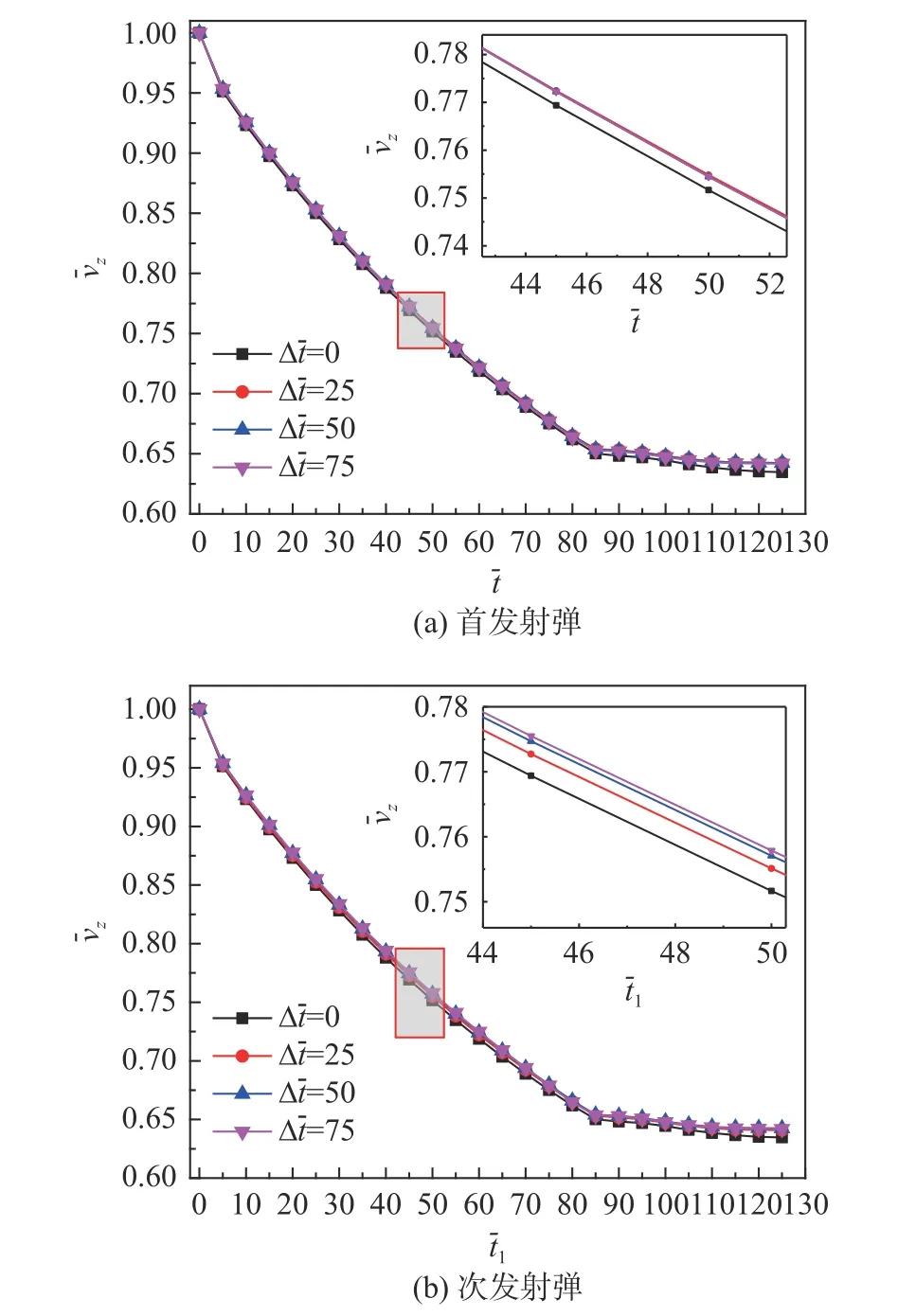
图14 出水过程射弹无量纲竖直速度衰减曲线Fig.14 Attenuation curves of dimensionless vertical velocity during the projectiles exiting water in vertical direction
图15 表示出水过程中射弹的阻力系数变化。射弹起始运动时,射弹大部分还处于沾湿状态,受到水的阻力较大,随着超空泡的生成,射弹被超空泡包裹,只有头部沾湿,射弹受到水的黏性阻力几乎为0,主要为压差阻力,此过程射弹的阻力系数比较稳定。随着射弹穿越自由面进入空气中,射弹头部周围的流体介质由水变成空气,密度值显著降低,导致射弹受到的阻力变成了量级很小的空气阻力值,这时阻力系数不妨标记为0。首发射弹和次发射弹出水过程的阻力系数曲线的变化趋势基本一致;相比异步发射,同步发射条件下射弹阻力系数的平均值略大。需要注意的是,Δ=75 时,次发射弹的阻力系数从=70(对应=145)时刻起出现增大,其原因为次发射弹受到附近溃灭空泡产生的局部高压影响,引起次发射弹受到的压差阻力增大(见图9)。
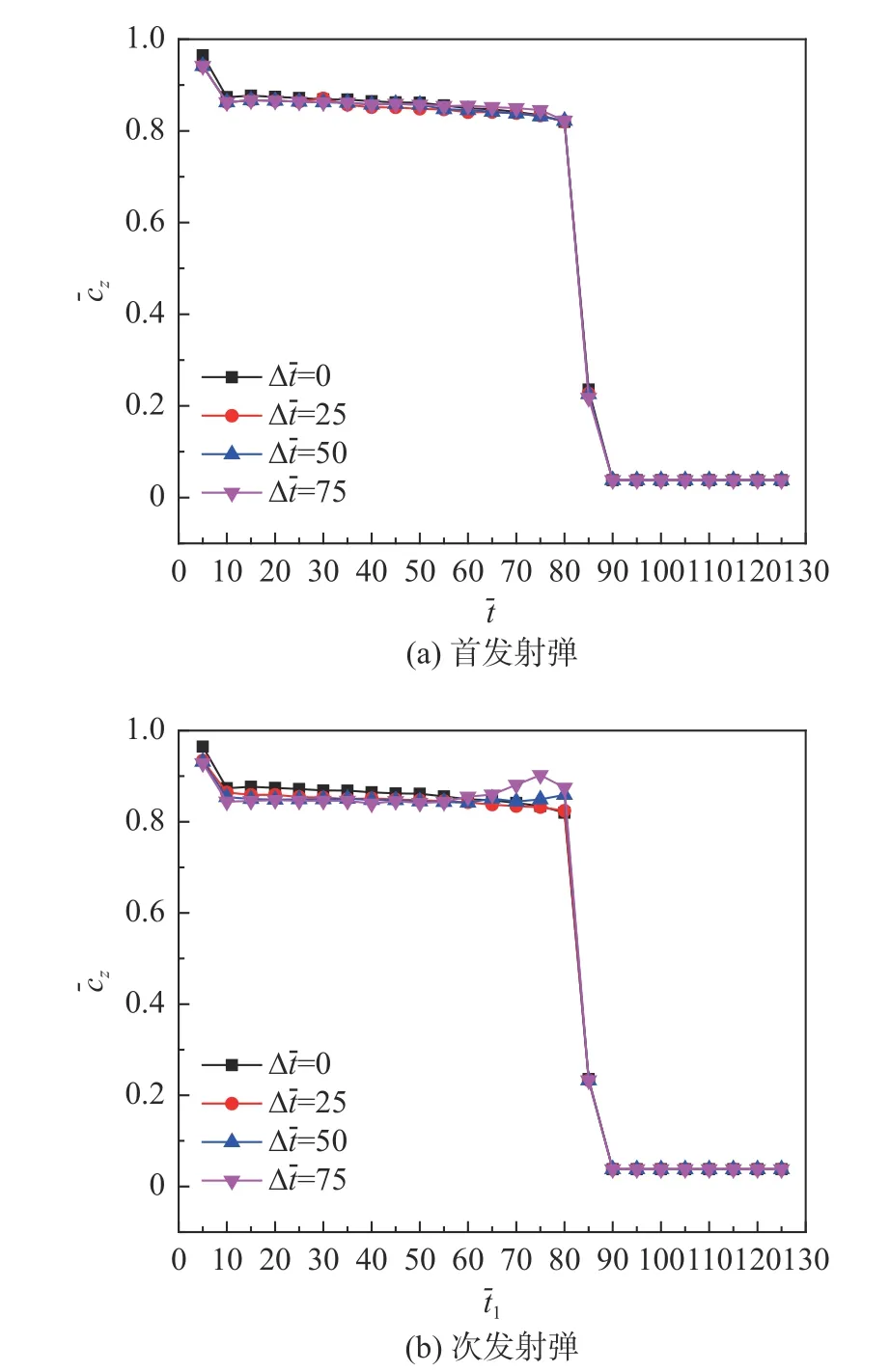
图15 出水过程中射弹的阻力系数变化Fig.15 Variations of drag coefficients during the projectiles exiting water
4 结论
本文基于求解N-S 方程的VOF 方法,采用重叠网格技术对高速射弹齐射出水问题进行了数值模拟研究,获得的主要结论如下:
1)同步发射出水时,两发射弹的超空泡流场互相影响,超空泡内侧扩张受到抑制,引起射弹超空泡外侧前沿轮廓曲率大于内侧,在出水阶段出水超空泡发生了非对称性溃灭。异步发射出水时,首发射弹超空泡前沿轮廓基本对称,而次发射弹超空泡前沿轮廓内侧壁面发生膨胀,失去了对称性,随着发射无量纲时差的增大,次发射弹超空泡内侧前沿轮廓曲率变小。
2)出水过程中,同步发射条件下两发射弹的弹道稳定性较差,两射弹先发生向外侧的偏转,随后向内侧偏转,其偏转角的最大值达到了3.1°。异步发射条件下首发射弹有很强的弹道稳定性,运动轨迹沿竖直方向向上运动,偏转角基本为0°;次发射弹在压差作用下向内侧偏转,运动轨迹也向内侧偏移,运动过程中次发射弹的最大无量纲水平位移和最大偏转角随发射时差的增大而减小,当发射无量纲时差为70 时,次发射弹的偏转角几乎为0°。
3)相比异步发射出水,同步发射出水射弹的无量纲竖直速度衰减较快,降低了射弹的减阻性能。
