非结构高阶CPR 方法的子单元限制中的问题单元侦测

石国权，燕振国，朱华君，*，马燕凯，贾斐然，2

(1.空气动力学国家重点实验室，绵阳 621000；2.西北工业大学 动力与能源学院，西安 710000)

0 引言

近年来，计算流体力学（Computational Fluid Dynamics，CFD）快速发展，不管是基础理论研究还是工程实际应用都需要进行精细的流场结构模拟。对于旋涡、分离、湍流等复杂流动现象，低阶格式数值耗散和色散较大，难以给出精细的流场结构（计算代价远远大于高阶精度格式），需采用耗散和色散小的高阶精度计算格式（3 阶及以上）[1]。另一方面，对复杂构型有着良好适应性的非结构网格，生成简单，且随机的数据结构非常利于网格自适应，非结构网格算法受到国内外学者重视[2]。近年来发展的高阶CPR方法是一种既适用于结构网格[3]，也适用于非结构网格[4]的紧致的差分型格式，具有很高的计算效率。

CPR 方法最早是由Huynh[3]在2007 年为求解结构网格下的双曲守恒律方程提出的，当时被称为通量重构（flux reconstruction，FR）方法。一维FR 方法可以直接利用张量计算推广到四边形网格和六面体网格上。2009 年，Wang 和Gao[4]将FR 的概念推广到了二维三角形网格及混合网格上，提出了提升配点惩罚(lifting collocation penalty,LCP)方法。由于FR 和LCP方法紧密联系，相关学者将其统称为CPR 方法[5]。

CPR 方法在选择特殊的求解点和修正函数时，在线性方程情况下可以等价于间断Garlerkin（discontinuous Galerkin，DG）方法、谱差分（spectral difference，SD）方法等，同时呈现出更简化的形式，计算量又相对较小[3]。具体来看，DG 方法在求解过程中涉及到通量函数的积分，计算量较大，而CPR 方法是基于求解点的差分型方法，没有积分计算的过程，因而计算方便且复杂度较低。此外，由于CPR 方法在具体计算某个单元内的函数值时，只需要利用与其直接相邻单元的函数值，因此CPR 格式具有紧致的特点，方便进行并行计算，适合求解大规模复杂构型流动问题。

但CPR 方法是高阶线性格式，在捕捉较强间断时，容易产生明显的虚假振荡，需要发展适合非结构CPR 方法的激波捕捉策略。目前对间断问题，常见的限制技术有添加人工黏性[6-8]、添加限制器[9-11]、采用混合格式[12-13]等方法。这些常见的限制技术已有学者将其推广应用到CPR 方法中，如MLP 方法[14]、人工黏性方法[15]、斜率限制器[16]、WENO 限制器方法[17]等。值得一提的是子单元限制技术的发展。Persson 和Peraire[7]提出，对高阶多项式近似，分辨率为 δ～h/p（h是 单元尺度，p是多项式阶数），激波通常跨越2～4 个单元，而划分子单元的做法可以将激波限制在子单元层面。如高阶DG 方法在单元内构造了高次多项式分布，具有高分辨特性，子单元限制技术可以在激波捕捉过程中尽可能地保持这种高分辨特性。Huerta 等[18]提出的用于DG 单元内分段积分常数的激波捕捉方法、Dumbser 等[19-20]基于多维最优阶 侦 测（multi-dimensional optimal order detection，MOOD）方法提出的后验子单元有限体积限制器、Kochi 和Ramakrishna[21]提出的DG 上的紧致子单元加权本质无振荡（compact subcell weighted essentially non-oscillatory，CSWENO）限制方法、Guo 等[22]提出的用于守恒律方程激波捕捉的三阶WCNS-CPR 混合格式，都是基于子单元的思想进行子单元激波捕捉格式的构造。但是这些方法中子单元等距分布，需要考虑主单元与子单元之间的数据交换。Hennemann 等[23]提出可压缩Euler 方程的高阶分裂形式DG 的熵稳定子单元激波捕捉方法，基于Gauss-Legendre-Lobatto（GLL）求解点，设计了一种非等距的子单元限制方法。Sonntag 和Munz[24]也提出了一种DG 方法的FV子单元限制方法，子单元划分方式选取了Gauss积分权值作为子单元的边长。非等距剖分下的子单元限制过程中，子单元的值直接由主单元上求解点的值得到，避免了平均划分子单元时所遇到的主单元与子单元之间的数据传递问题。这些子单元限制方法的基本思想是侦测到问题单元后，将其剖分为子单元，然后在子单元上采取具有激波捕捉能力的格式。从这个角度来看，子单元限制属于混合格式的范畴。

我们前期针对二维结构网格提出了一种高阶CPR 方法的子单元限制方法[25]并推广到非结构四边形网格[26]，在光滑单元上采用CPR 方法，问题单元上采用二阶非等距非线性加权激波捕捉格式。该子单元限制方法使用扩展多项式的最高模态衰减（highest modal decay of the extended polynomials,MDHE）激波侦测因子[23]侦测问题单元。本文在文献[25]的基础上，基于非结构四边形网格CPR 方法的子单元限制方法，讨论了单元混合策略和分维混合的可行性，并对比了不同问题单元侦测因子下的结果，为间断有限元类高阶格式（DG、CPR、SD 等）的子单元限制提供可靠的参考。

1 控制方程及离散

1.1 控制方程

考虑守恒形式的二维Euler 方程

式中，U是守恒变量，F、G是通量。

式中，ρ 为密度，u、v为速度，p为 压力，E为总能。对理想气体，比热比 γ=1.4。

1.2 二维非结构四边形网格上的CPR 方法

首先，建立物理空间中的四边形网格单元与计算空间中的标准单元I=[-1,1]×[-1,1]之间的坐标变换关系：

式中，L是用来定义四边形的点的个数，在直边四边形中L=4对 应4 个顶点，(xl,yl)是这些点的笛卡尔坐标，Ml是形状函数。Jacobi 矩阵形式如下：

假设该矩阵非奇异，则其逆矩阵为：

式中，

将Euler 方程（1）变换到计算空间后，变为：

每个单元上的通量值利用单元内部K×K个求解点处的通量值构造多项式得到。二维情况下，通量的插值多项式为：

式中，Lk是Lagrange 多项式。此时的通量多项式函数是间断通量函数，单元界面通量不连续，会破坏守恒律，需要构造连续通量多项式函数，即：

式中，gL、gR是K次多项式修正函数，满足：

在CPR 的计算过程中，需要求解通量导数。Huynh[3]基于通量的Lagrange 插值多项式和Riemann通量对间断通量函数进行修正，将界面处间断通量函数与Riemann 数值通量的差量引入到单元内部，构造连续的通量函数，建立了单元间的联系。求解点处的通量导数可由连续通量函数式（14）直接求导。最终得到计算空间中的空间离散方程：

本文采取五阶CPR 格式，求解点选择五点Gauss-Legendre 点，单元界面处的Riemann 通量选择局部 Lax-Friedrichs 通量。Riemann 通量基于原始变量计算，原始变量在界面的左右值通过基于求解点的插值多项式得到，多项式的形式与式（12、13）相同。修正函数选择文献[3]中gDG修正函数：

式中，PK是Legendre 多项式。

时间离散格式采取三阶Runge-Kutta 格式，用RHS表示式（1）的右端项：

则三阶Runge-Kutta 格式为：

式中，j是单元序号，k、l是四边形单元内部求解点序号，dt是时间步长。

2 子单元限制策略

本文子单元限制策略的主要思想是，利用问题单元侦测因子标记流场中含有大梯度或是间断的不光滑单元为问题单元，然后将这些问题单元按照求解点位置划分为非等距子单元，在子单元上添加限制措施。

2.1 问题单元侦测因子

本文的重点在于介绍不同侦测因子对结果的影响，选择了目前较为流行的TVB[12,27]、MDH[23,25-26]、JST[24,28]三种问题单元侦测因子进行对比。下面简单介绍这三种侦测因子的基本方法。

2.1.1 TVB 侦测因子

总变差有界（total variation bounded,TVB）是有限体积中经典的minmod 型限制器[27]。Qiu 等[12]基于TVB 构造了问题单元侦测因子，每当minmod 限制器试图改变斜率时，单元就被标记为问题单元。

TVB 限制器的思想是：

式中，

若(a1,a2,···,ak)没 有返回a1值，则说明此单元是问题单元，定义问题单元指示器 β=1，否则为光滑单元，定义 β=0。式（24）中的M是人工定义的常量，通过改变M的大小可以调节问题单元判断条件的严格程度。

2.1.2 MDHE 侦测因子

正如文献[7]中提到的那样，解的表达多项式的最高模态能量系数在光滑区域会迅速衰减，而在非光滑区域则衰减较慢，表征了单元的光滑程度。因此，可以针对最高模态定义阈值，来判断单元内是否存在间断。该方法被称作最高模态衰减（highest modal decay,MDH）方法[23]。Hennemann 等使用最高和次高模态系数改进了此方法以避免奇偶效应[29]，但是只利用了单元内部求解点，对于存在于单元界面处的间断可能无法识别。我们前期通过引入左右界面处Roe 平均值构造新的多项式[25]，构造新的多项式所用模板为 {u0,u1,···,uK+1}，其中u0和uK+1为左右界面处Roe 平均值。Roe 平均值基于界面通量点附近的两个求解点值计算得到[30]。由于它是通过扩展MDH 侦测因子的多项式阶来构造的，所以它被命名为MDHE[26]。一维多项式的模态能量定义为：

式中，K是单元内求解点个数，是模态系数，P j（j=0,···,K+1）是 Legendre 基函数，取 ∊=ρp为侦测变量。解的多项式可以表达为Lagrange 多项式展开式：

也可以表达为Legendre 基函数展开式：

基于最高和次高模态能量的占比定义为：

定义阈值为：

按照大量算例测试的经验[23]，式（30）中取a=0.5、c=1.8 。如果IE＞IT，则单元被标记为问题单元，并定义 β=1；否则判定为光滑单元，β=0。

2.1.3 JST 侦测因子

JST 侦测因子源于Jameson 等[28]提出的经典的Jameson-Schmidt-Turkel（JST）方法。该方法根据基于压力梯度的开关函数将人工二阶和四阶耗散项添加到欧拉方程以抑制振荡。Sonntag 等[24]在研究DG 方法的子单元限制策略中，改进了JST 侦测因子。本文采用该改进形式的JST 侦测因子。

一维情况下：

式中，k代表单元内部求解点的局部坐标索引，pmin,k=min(pk±d,d=1,2,3)是求解点附近节点值的最小压力，pmax,k=max(pk±d,d=1,2,3)是求解点附近节点值的最大压力。

二维情况下考虑两个方向：

式中，k、l代表单元内部求解点的局部坐标索引，pmin,k,l=min(pk±d,l±d,d=1,2,3)，pmax,k,l=max(pk±d,l±d,d=1,2,3)。在非结构四边形网格中，模板由本单元及共边的相邻单元提供。式（32）给出了每个子单元或CPR 求解点处的指示值，使用体积加权，得到单元的单个指标值：

式中，K是单元内 ξ 或 η方 向的求解点个数，VElement和Vk,l在标准单元上计算，分别是标准单元和子单元的面积。

如不特殊说明，我们取阈值IT=0.01来判断间断的存在。当IJST＞IT时，认为该单元是问题单元，记为β=1。另外，侦测变量的选取与文献[24]一致，使用压力p作为侦测变量。

2.2 基于非等距非线性插值的子单元激波捕捉格式（CNNW2）

在子单元上采取常值分布函数可以构造类似于Godunov 格式的一阶迎风格式，但是一阶格式的耗散太大，分辨率会严重下降。为提高子单元上的分辨率，在前期的工作中[26]，我们将Zhu 和Liu 等[24]提出的用作五阶CPR 方法的子单元限制器的二阶紧致非等距非线性加权格式（CNNW2）推广到了非结构网格。由于该子单元限制方法也是一种局部混合格式，故称作CPR-CNNW2 格式。

这里我们简要介绍一下CNNW2，详细可见文献[26]。非等距子单元的划分如图1 所示，子单元的求解点与CPR 单元的求解点重合[23]（红色圆点是Gauss 求解点，视作子单元“中心”；蓝色方块是子单元通量点，视作子单元边界），避免了子单元等距剖分下，主单元与子单元之间的数据交换的麻烦。每个子单元的长度可以表示为ξfpi+1-ξfpi=ωi，（i=1,2,…,K），其中：ωi为 Gauss 积分权；ξfpi为通量点位置，ξf p1=-1。

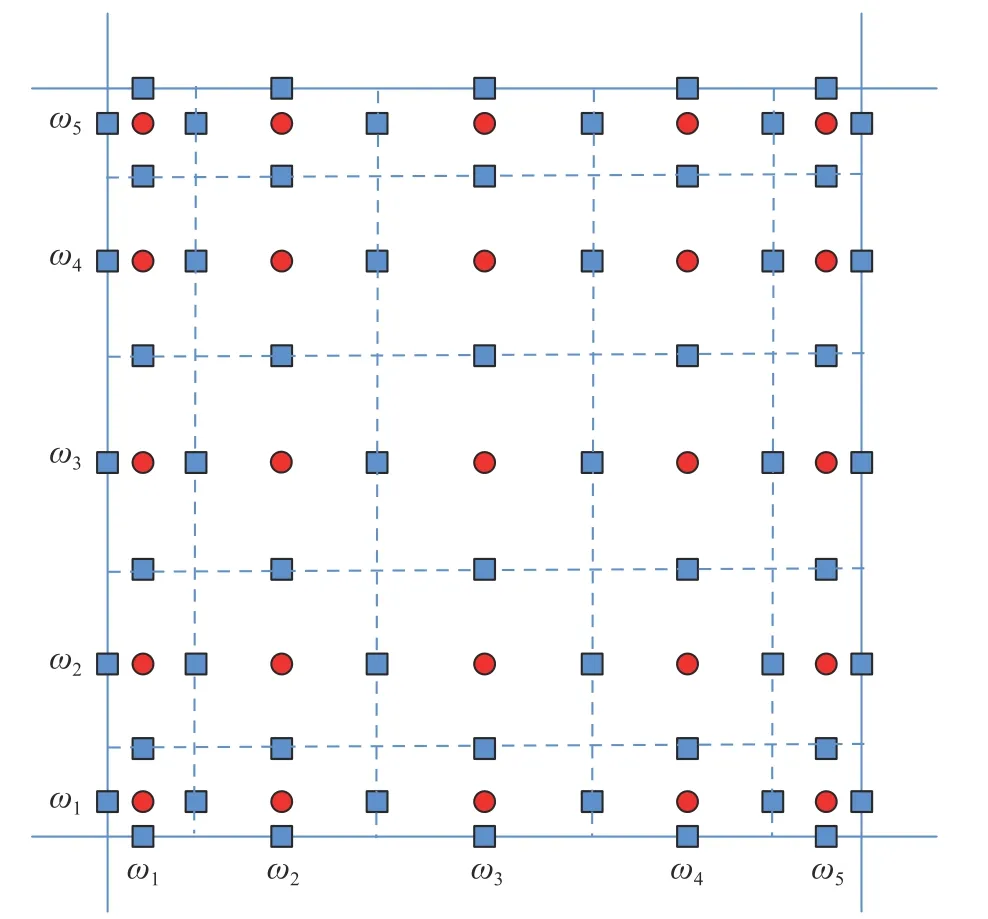
图1 子单元划分方式Fig.1 Layout of subcell division

对于五阶CPR，考虑单元五个Gauss 求解点的中间三个求解点对应的子单元，以第二个求解点为例，如图2 所示，CNNW2 插值利用标准单元内部三个求解点得到通量点处的值。

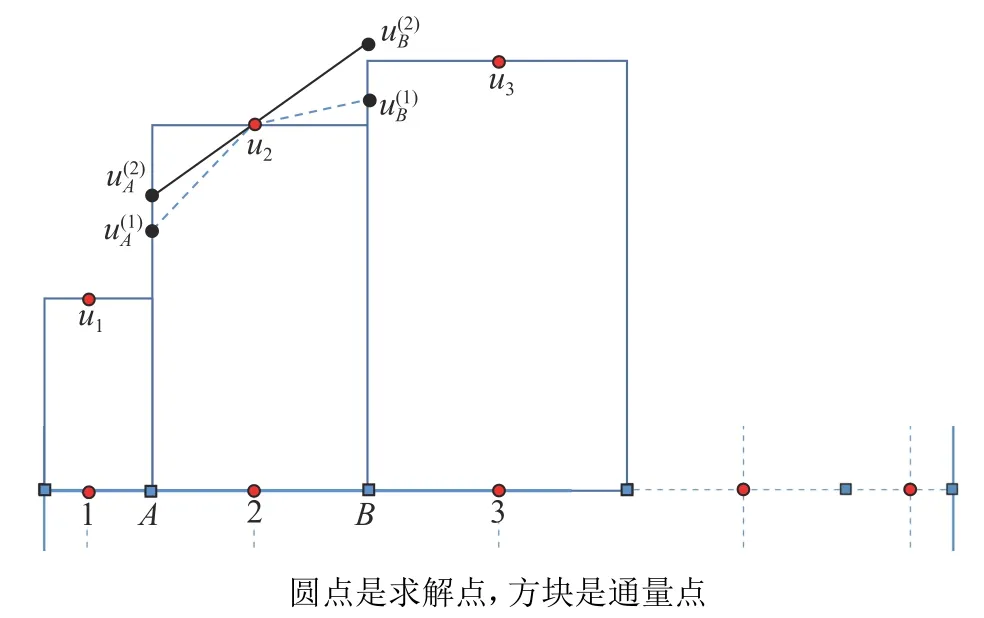
图2 二阶非等距非线性插值模板Fig.2 Stencil for the second-order nonuniform nonlinear interpolation

具体求解步骤如下：

4）添加限制器控制数值振荡，得到最终的子单元界面处物理量的逼近值。

式中限制器为：

式中，m=min(u1,u2,u3),M=max(u1,u2,u3)。

再考虑非结构四边形单元，每个方向上界面附近的两个求解点u1和u5对 应的子单元。图3 是求解u1对应子单元的情况，插值过程只在求解界面处时涉及到单元之间的数据处理。将的计算由计算空间改为物理空间上进行（反距离加权代入物理空间距离），在物理空间上计算得到。

图3 物理空间上插值模板Fig.3 Interpolation stencil in the physical space

插值过程使用特征变量，根据以上插值方法得到子单元界面的左右值，特征投影的过程参考文献[30]。最终得到子单元界面的原始变量，进而计算子单元界面处的Riemann 通量。半离散形式使用二阶差分算子：

问题单元内部的子单元分布是结构化的，由一维空间离散格式可以直接推广得到二维空间离散格式。

2.3 CPR-CNNW2 混合策略

2.3.1 格式切换

一个单元所采用的格式由问题单元指示器 β决定，当 β=1时 采用CNNW2，当 β=0时采用CPR。问题单元指示器的值发生变化，格式对应地进行切换。单元与单元的交界面处需要计算共用的Riemann 通量。Riemann 通量的左值和右值的求解方式根据单元是否为光滑单元而定，对于CPR 单元和CNNW2 单元的界面，假设左侧单元为CPR 单元，右侧为CNNW2 单元。左值由光滑单元提供，使用CPR 中的Lagrange 插值获得；右值由问题单元提供，使用二阶非等距非线性插值获得，然后得到Riemann 通量为：

也就是说，从求解点到界面通量点的插值方法由单元的类型进行控制。

2.3.2 单元/分维混合CPR-CNNW2 格式

四边形网格中，问题单元的侦测是逐维进行的，当单元内任一行/列被标记为问题单元，则整个单元都被标记为问题单元。按照问题单元分布，以整个单元为基本单元进行CPR-CNNW2 格式的切换计算，称作单元混合CPR-CNNW2 格式。

单元混合CPR-CNNW2 格式是常见的一种混合方法，但在四边形网格CPR 方法中，计算是逐维进行的。在单元内部只标记出现问题的行或列，如二维问题中激波附近区域的求解点的空间离散，在一个方向使用CNNW2 格式，另一个方向使用CPR 的模式是可行的，我们称之为分维混合CPR-CNNW2 格式，如图4。特定情况下，采用分维侦测可以减少侦测单元，提高格式分辨率，同时提高计算效率。我们在算例测试中，测试了分维混合CPR-CNNW2 格式下不同侦测因子的表现。

图4 分维混合CPR-CNNW2 示意图Fig.4 Schematic of the hybrid CPR-CNNW2 scheme by dimension

2.4 子单元时间步长限制

CPR 和DG 方法的CFL 数是和多项式阶数有关的，参照Dumbser 在文献[19]中提到的时间步长限制：

式中，d是空间维度，N是多项式阶数，h代表网格尺寸，|λmax|是最大特征波速度。对二维Euler 方程，其特征矩阵A(U)=∂F/∂U的特征值λA=[u-c,u,u,u+c]，特征矩阵B(U)=∂G/∂U的特征值 λB=[v-c,v,v,v+c]。令

式中，Δdj是相邻单元重心距离最小值。Dumbser[19]利用CFL 条件得到DG 的时间步长限制下，等距子单元的最大划分个数为Ns=2N+1，其中N是多项式次数。当Ns＞2N+1时，子单元时间步长限制会反过来约束DG 的最大时间步长。本文的非等距划分子单元方式，标准单元内子单元尺寸符合Gauss 积分权分布，和求解点个数相关，最小的为第一积分权 ω1代表的子单元长度。CPR 格式使用五阶精度，Guass 积分使用五点格式时，ω1＞1/(2N+1)。故在此可以统一使用CPR 的时间步长限制。

3 算例测试

3.1 Sod 激波管问题

Sod 激波管问题的初始条件为：

采用单元数为40，左右边界为Dirichlet 边界条件，计算终止时间为T=0.2，CFL=0.5，对三种激波侦测因子下的CPR-CNNW2 的计算结果进行对比。在此算例中TVB 侦测因子的自由参数取M=100.0。

计算结果如图5 所示。为了方便对比三种激波侦测因子下的问题单元分布，将图5 右侧纵坐标轴设为问题单元指示器 β，并将三种方法错位分布。在接触间断x=0.7 和x=0.85 附近，使用三种问题单元侦测因子都无明显振荡。对比之下，无论采取何种侦测方式，混合CPR-CNNW2 格式都比CNNW2 格式对间断的抹平小。虽然三种侦测因子最终的侦测结果中，问题单元只存在于间断附近，但可以看到采取TVB方法对接触间断的抹平较大，而MDHE 和JST 方法对间断的抹平较小，数值表现更好。

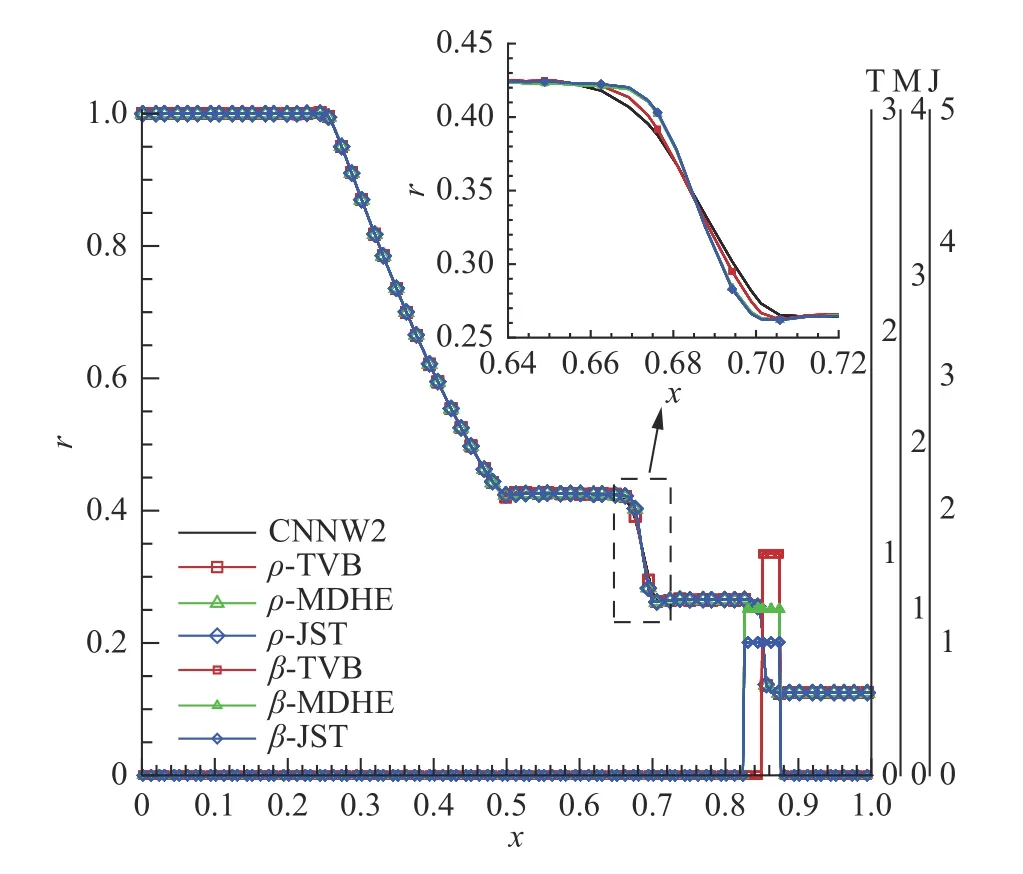
图5 Sod 激波管的密度分布和问题单元分布图Fig.5 Distributions of the density and problematic cells for the Sod shock tube problem

3.2 Shu-Osher 问题

Shu-Osher 问题的初始条件为：

采用单元数为100（对应DoFs=500），左右边界分别为流入流出边界条件，计算终止时间为T=0.18，CFL=0.9 。在此算例中TVB 侦测因子的自由参数取M=3.0。

计算结果见图6，其中参考结果为混合CPR-CNNW2格式在x方向DoFs=2 000 下的计算结果。混合格式在问题单元采取低阶格式计算，在流场的大部分光滑区域采取高阶CPR 方法计算，能够显著提高算法的分辨率。通过比较得到，MDHE 侦测因子下的分辨率最高，JST 次之，TVB 最低，相对应的问题单元占总单元数分别为5%、9%、23%。这反映了问题单元侦测区域与分辨率之间的关系：问题单元越多，即采取二阶格式计算的单元越多，引入的耗散越大，分辨率越低。问题区域的分布随时间变化见图7，TVB 侦测标记的问题单元较多，尤其是在高频振荡区，无法有效识别问题单元，这也导致了在高频振荡区TVB 侦测因子下混合CPR-CNNW2 格式的结果几乎和CNNW2的结果重合，而MDHE 和JST 的结果具有更高的分辨率，表现较好。

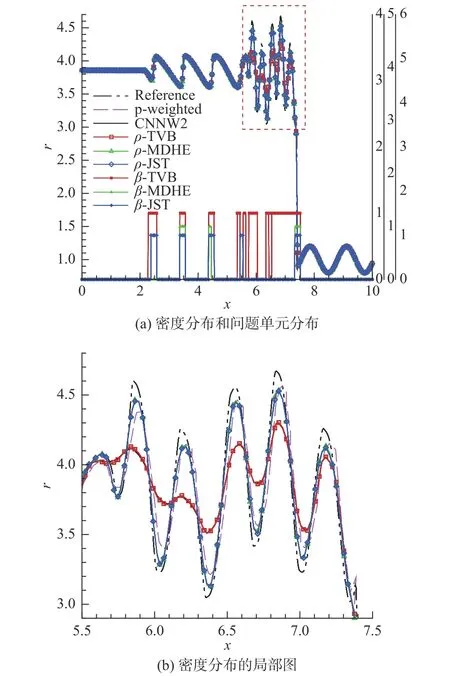
图6 Shu-Osher 问题的密度分布和问题单元分布Fig.6 Distributions of the density and prolematic cells for the Shu-Osher problem

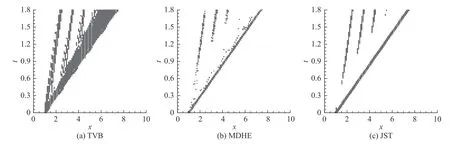
图7 问题单元随时间变化的分布图Fig.7 Distributions of problematic cells over time

另外，我们将本文的CPR-CNNW2 结果与文献[31]中的p-weighted 限制器在取p=5次多项式时采用Nc=100（DoFs=600）网格下的计算结果进行对比。可以看到在高频振荡区，MDHE 和JST 侦测因子下的计算结果的分辨率比p-weighted 限制器的计算结果稍好。

3.3 等熵涡测试

二维等熵涡问题的初始条件是在一个均匀流上添加一个各向异性的等熵旋涡的扰动。初始条件设置见文献[32]，取自由度为200×200，时间步长dt=0.000 1，计算到T=1.0。基于等熵涡问题，对CNNW2与CPR 的计算时间进行对比测试。

我们通过调节TVB 侦测因子中的参数M减小阈值，将一些光滑单元设置为问题单元，对比单元混合策略和分维混合策略的计算时间，如表1 所示。在相同的侦测阈值和计算条件下，分维混合策略的计算时间比单元混合花费时间略少，计算效率更高。但是在单元混合下，四边形单元出现不满足条件的维度时便可定义为问题单元，分维混合下需要计算所有维度。故在侦测时间上，分维混合所花费的时间较多。

表1 单元混合与分维混合的计算时间Table 1 Calculation time for hybrid by cell and by dimension

另外，调整不同侦测因子的自由参数使侦测到的问题单元占比为0，以测试不同侦测因子对计算时间的影响。由表2 中计算时间可知，在相同计算网格下，CPR 计算效率比CNNW2 高。另外，对比分维混合CPR-CNNW2 格式和单个CPR 格式，侦测因子会带来额外的计算量。表2 中单个CPR 的计算时间和侦测时间的总和与混合格式的总计算时间大致相同（相对误差小于1%），观察侦测时间的影响，MDHE侦测因子占总计算时间的6.71%，TVB 和JST 侦测因子计算开销更多。问题单元的占比对计算时间有一定影响，问题单元越多，采取CNNW2 格式计算的单元越多，计算效率越低。同时，侦测因子本身的计算时间也会对总计算时间产生影响，计算时间最小的是MDHE 侦测因子。

表2 不同侦测因子对计算时间的影响Table 2 Influence of different indicators on the calculation time

3.4 双马赫反射

双马赫反射的初始条件为：

要提到的是，TVB 侦测因子鲁棒性比较差，为解决这个问题，我们引入了过渡单元[22]，把问题单元的共边相邻单元也标记为问题单元，增加了侦测区域。双马赫反射问题计算结果见图8、图9。从图8 可以看出，三种侦测因子下CPR-CNNW2 都能准确地捕捉到马赫杆。JST 侦测下的计算结果中剪切涡更明显，分辨率更高，TVB 侦测与MDHE 侦测下的计算结果相差不大。对比问题单元的分布，TVB、MDHE 和JST 侦测因子标记的问题单元占总单元数分别为22.66%、3.84%、3.71%。TVB 侦测因子标记的问题单元最多，MDHE 明显少了很多，但是密度等值线结果的分辨率相差不多。JST 侦测因子下剪切涡附近的问题单元最少，所以对剪切涡的影响最小，分辨率最高。

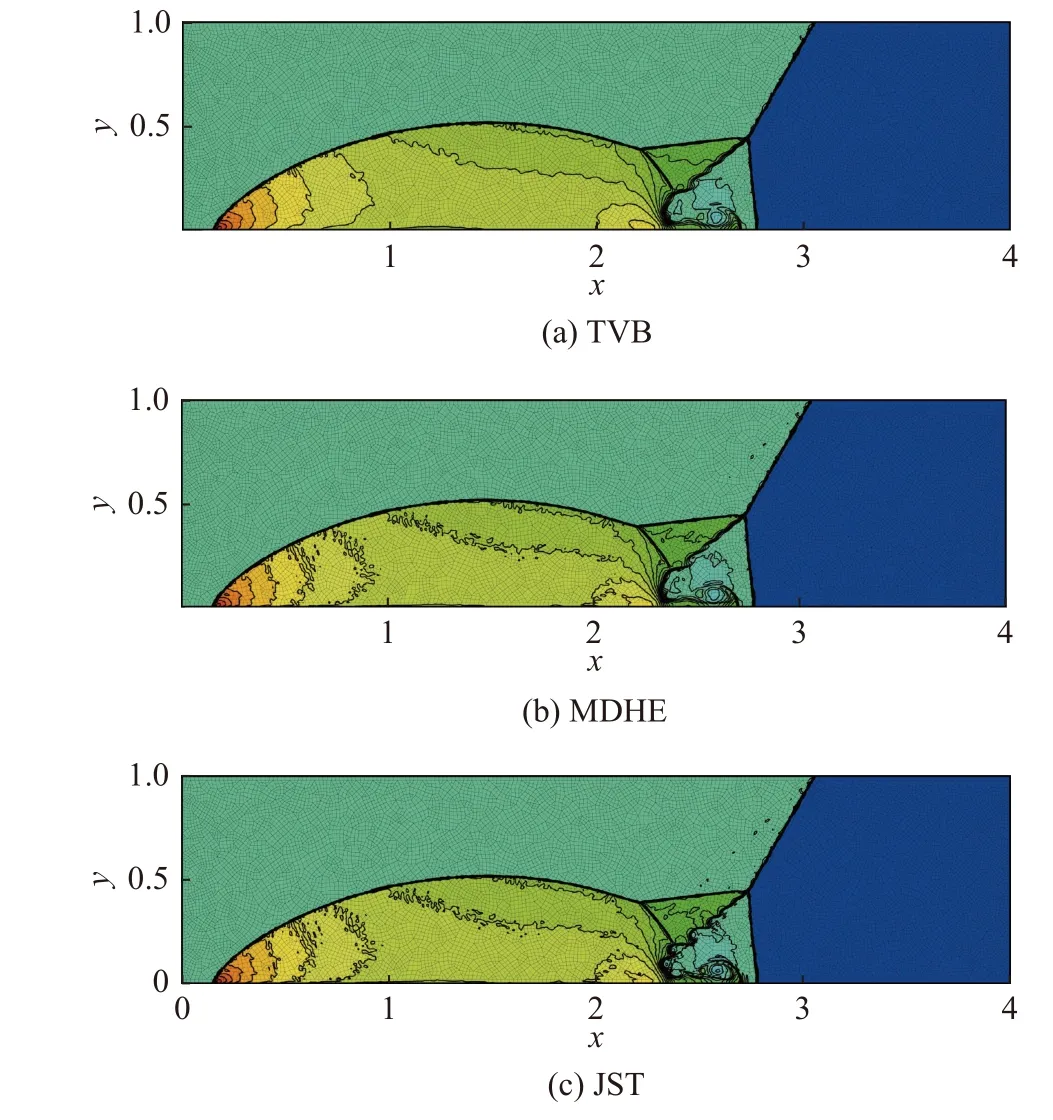
图8 CPR-CNNW2 在不同侦测因子下求解双马赫反射问题（从1.5 到21.7 的30 条密度等值线）Fig.8 Density contours with 30 levels ranging from 1.5 to 21.7 for CPR-CNNW2 with different indicators in the double Mach reflection problem

图9 双马赫反射问题的各种侦测因子下的问题单元分布图Fig.9 Distribution of problematic cells under different indicators for the double Mach reflection problem

从对比结果中可以看出，不同的问题单元侦测因子，侦测问题单元的区域不同，对计算结果的影响不同。问题单元越多，计算时间越长，分辨率越低。

由于TVB 侦测因子在分维混合计算双马赫问题，即使加上过渡单元且参数M取到1 ×10-6，依然计算失败，故以MDHE 和JST 侦测因子测试分维混合下的CPR-CNNW2 方法。双马赫问题计算结果密度等值线见图10（a、b）。图10（c、d）中红色区域内的求解点 ξ、η两个方向都采取CNNW2 格式，绿色部分只有一个方向采取CNNW2 格式计算。分维混合计算会使鲁棒性下降，我们按照一维形式增加了过渡单元。其中JST 侦测器在阈值不变的情况下计算稳定，而MDHE 侦测器需要减小阈值才能稳定计算。从图10（c、d）可以看到，过渡单元的添加和阈值的降低有可能会造成分维侦测的问题单元多于单元侦测的问题单元。在鲁棒性上，JST 侦测器的表现要好于MDHE 侦测器，但是JST 侦测因子下的计算结果仍需关注边界处出现局部振荡的现象。分维混合计算需要结合适合的问题单元侦测因子，才能更好地发挥减少问题单元区域、提高计算结果分辨率的优势。

图10 双马赫反射的分维混合CPR-CNNW2的计算结果Fig.10 Numerical results of CPR-CNNW2 with detecting by dimension for the double Mach reflection problem

3.5 激波-旋涡干扰

激波-旋涡干扰问题初始条件设置可以参考文献[33]。在该问题中，运动的旋涡和静止激波相互干扰，发展出具有平滑特征和间断的复杂流动结构，常用来测试格式捕捉激波和维持分辨率的能力。计算域[0,2]×[0,1]，初始条件由位于x=0.5的静止激波Ms和 中心位于 (xc,yc)=(0.25,0.5)的 旋涡Mv给出。其中旋涡Mv的切向速度表达式为：

式中，r2=(x-xc)2+(y-yc)2，vm是最大速度。

采用 120×60 (DoFs=600×300)的均匀网格计算该问题。左右边界为Dirichlet 边界条件，上下边界设置为壁面滑移边界条件，计算终止时间为T=0.7，CFL=0.9 。本算例中，TVB 侦测因子参数M=100.0，JST 侦测因子阈值IT=0.02。

3.5.1 单元混合CPR-CNNW2 格式计算结果

计算结果如图11、图12。从图11 中，明显观察到TVB 侦测因子下的结果在旋涡附近的分辨率明显不如MDHE 和JST 侦测下的计算结果，但相对于单一CNNW2 格式计算结果，分辨率改善很多。图12 中的TVB、MDHE、JST 三种侦测因子标记的问题单元区域占比依次为3.01%、1.72%、1.67%，且TVB 在旋涡处标记了较多问题单元，对耗散的引入比较大。

图11 不同侦测因子下CPR-CNNW2 求解激波-旋涡干扰问题的计算结果Fig.11 Numerical results of CPR-CNNW2 with different indicators for the shock-vortex interaction problem

图12 激波-旋涡干扰问题的问题单元分布Fig.12 Distribution of problematic cells for the shock-vortex interaction problem

为了更精细地对比，在不同结构特征处，通过截线进行定量分析[34]，两条截线分别为截线①（y=0.40）和截线②（x=1.05），如图13 所示。CNNW2 格式和三种侦测因子下的单元混合CPR-CNNW2 格式在截线处的密度分布结果见图14。从图中看出，TVB 侦测因子下旋涡处的耗散远大于JST 和MDHE 侦测因子下的结果。其次，从问题单元占比随时间变化的情况（见图15）可以看出，整个求解过程中TVB 的问题单元最多，MDHE 次之，JST 最少。问题单元侦测区域的大小不仅和侦测因子类型相关，也和阈值的设置相关，如图15 中黑色实线为JST 侦测因子阈值IT=0.01时问题单元的时间历史，旋涡区域也被标记为问题单元，引入耗散过大。MDHE 和JST 表现的微小差距和阈值的设置也是有关的。

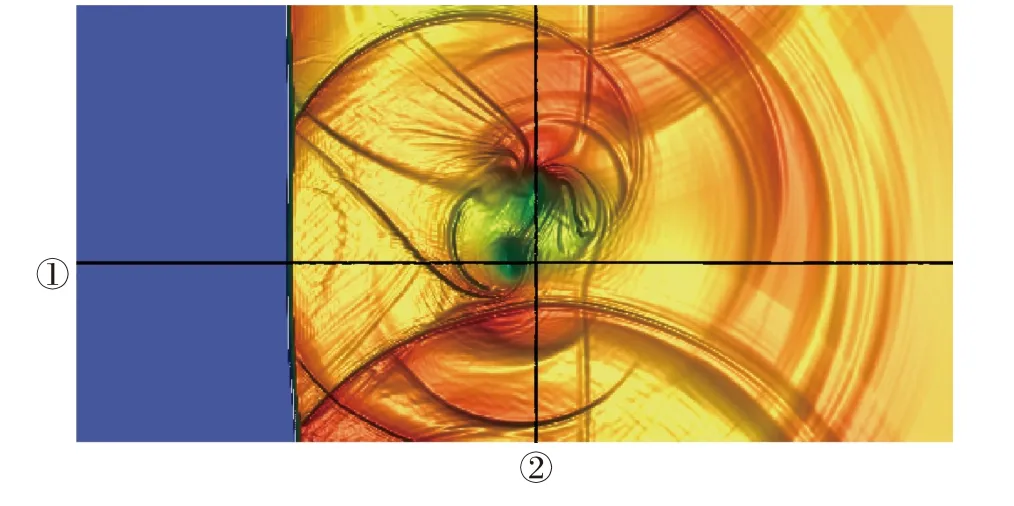
图13 激波-旋涡干扰问题的参考线位置Fig.13 Reference lines for the shock-vortex interaction problem

图14 不同侦测因子下单元混合CPR-CNNW2 格式在两条截线上的密度分布图Fig.14 Density distribution along the two sliced lines of CPRCNNW2 with detecting by cell for different cell indicators

图15 单元混合下CPR-CNNW2 格式问题单元占比随时间变化图Fig.15 Time variation of the problematic cell proportion for CPR-CNNW2 with detecting by cell

3.5.2 分维混合CPR-CNNW2 格式计算结果

图16 中展现了三种侦测因子下分维混合CPRCNNW2 方法在截线处的密度分布结果。在当前阈值下，MDHE 分维侦测下的计算结果分辨率在三者之中最高。另外从图17 可以看到，分维混合CPR-CNNW2方法下的问题单元分布和激波的分布相关。

图16 分维混合CPR-CNNW2 格式在两条截线上的密度分布Fig.16 Density distribution along two sliced lines for CPR-CNNW2 with detecting by dimension

图17 分维混合CPR-CNNW2 计算激波-旋涡干扰问题的问题单元分布Fig.17 Distribution of problematic cells of CPR-CNNW2 with detecting by dimension for the shock-vortex interaction problem

观察图18 中分维混合CPR-CNNW2 格式分别采取不同侦测因子的问题单元占比随时间变化情况，整个计算过程中，ξ 方向和 η方向的问题单元的占比相差很大，说明单元侦测的方式会标记“多余”部分。另外，最终的分维混合格式计算结果，MDHE 比JST 分辨率略高，可能是由于在T=0.1到T=0.4激波和旋涡干扰期间，MDHE 分维侦测比JST 分维侦测标记的问题单元少。

图18 分维混合CPR-CNNW2 格式的问题单元占比随时间变化图Fig.18 Time variation of the problematic cell proportion for CPR-CNNW2 with detecting by dimension

基于阈值对计算结果的影响，我们对比了三种侦测因子在不同阈值下的表现，其中TVB 侦测因子中分别设置M=100.0和M=10.0，MDHE 侦测因子中分别 设 置a=0.5和a=0.05，JST 侦 测 因 子 中 分 别 设 置IT=0.02和IT=0.01。如图19，相同侦测阈值下，分维混合策略比单元混合策略的分辨率高。需要注意的是，相比于其他两种侦测因子，在TVB 侦测因子下，分维的混合策略对结果的影响明显大于调整阈值的影响。而MDHE 侦测下，分维混合CPR-CNNW2 方法比单元混合分辨率更高，而且阈值越大，分辨率越高。JST 侦测下，分维侦测的影响较小，阈值的影响较大，阈值越大分辨率越高。

图19 截线y=0.40 上三种侦测因子在不同阈值下的密度分布Fig.19 Density distributions along the sliced line at y =0.40 for three indicators under different thresholds

3.5.3 CPR-CNNW2 格式与其他格式的对比

基于MDHE 侦测因子的分维混合CPR-CNNW2格式，在 400×200（DoFs=2 000×1 000）的矩形网格下的计算结果数值纹影（密度梯度云图）如图20 所示。在相同自由度下，与采用改进的五阶WENO-Z+格式[35]得到的计算结果相比，混合CPR-CNNW2 格式的计算结果流场细节更丰富。从图21 的截线处的密度分布结果来看，分维混合CPR-CNNW2 格式在旋涡处的分辨率更高。

图20 全局/局部数值纹影对比Fig.20 Global/local numerical schlieren comparison

图21 截线x=1.05 上CPR-CNNW2 和WENO 的密度分布对比Fig.21 Density distributions along the sliced line at x=1.05 compared between CPR-CNNW2 and WENO

4 结论

本文基于非结构四边形网格CPR 方法的子单元限制方法，对比了不同问题单元侦测因子对计算结果的影响，得到以下结论：

1）一维算例测试结果显示，不同侦测因子对结果的分辨率产生影响。TVB、MDHE、JST 三种侦测因子中，TVB 对结果的抹平最大，MDHE 和JST 的分辨率较高。

2）二维算例结果显示，基于多项式模态衰减的MDHE 侦测因子在侦测到很少一部分问题单元的情况下，计算稳定，而且侦测本身花费的时间较小。基于压力梯度的JST 侦测因子侦测到的问题单元也较少，但是侦测本身花费时间较多。而TVB 侦测因子对流场的适应性不强，对高马赫数问题需要采取一些措施提高鲁棒性，比如调整自由参数M或者添加过渡单元。

3）基于四边形单元分维计算的特点，测试了分维混合CPR-CNNW2 策略。和单元混合相比，分维混合可以提高分辨率。在含有明显方向特征的流场中，划分均匀网格并考虑分维侦测可以减少问题单元的标记，减小耗散的引入。激波旋涡干扰的算例显示，采取TVB 和MDHE 侦测因子时，分维混合策略计算稳定且结果分辨率更高；采取JST 侦测因子时，分辨率相差不大。同时，阈值的调整也会对计算结果的分辨率产生影响。

综合来看，MDHE 侦测因子计算过程花费时间少，对问题单元侦测比较准确，且在分维混合措施下对计算结果的分辨率有所提高，是一种适合于四边形网格的问题单元侦测因子。这三种侦测因子都需要人工设置参数，若不能有效准确地确定阈值，会造成计算的浪费。下一步我们将研究基于流场自适应选择阈值，进而减少人工干预，进一步提高计算效率。另外，通过将三角形单元分解为三个四边形单元的方式，该子单元限制方法可以推广到三角形网格或者混合网格，但这对网格质量的要求可能更高。