声涡相互作用下翼型分离泡内流动动力学特征
2023-03-13史泽奇钟伯文汤崇辉
史泽奇,刘 勇,*,钟伯文,汤崇辉
(1.南昌航空大学 飞行器工程学院,南昌 330063;2.江西省飞行器设计与气动仿真重点实验室,南昌 330063)
0 引言
许多工业中使用层流翼型设备,如小型无人飞行器、微型风力涡轮机等,在中等雷诺数(1×104≤Re≤1×106)条件下,层流翼型表面会出现层流分离泡(laminar flow separation bubble,LSB)的问题[1-3]。层流分离泡会使得翼型后缘产生自噪声(纯音噪声和宽频噪声),分离泡内某一频率的扰动被放大,从而形成纯音噪声,纯音噪声影响分离泡内对流不稳定性,形成噪声反馈回路,进一步增加远场噪声级[4]。随着小型无人机的快速发展,人们对噪声污染的要求越来越严格,纯音噪声的出现会使得这些设备使用受限[5-6]。因此研究声涡相互作用下层流分离泡内涡的动力学特征,对纯音噪声生成机理的理解及噪声控制有一定的意义。
Paterson 等[7]对二维NACA0012 和NACA0018翼型涡噪声研究中发现了离散纯音现象,并利用平板边界层的计算提出了离散纯音和主纯音噪声频率的经验公式。他们还观察到一种所谓的“阶梯型”频率变化:在局部,主纯音噪声频率随速度的变化而变化,然后突然发生跳跃。Tam 等[8]根据Paterson 的实验结果提出了一种反馈机制来解释梯形结构,他们认为在尾缘和噪声源之间存在自激励反馈回路。Lowson 等[9]实验显示纯音噪声的产生与压力侧存在分离泡有关。Nash 等[10]证明了翼型压力侧边界层的不稳定性对纯音噪声现象起重要作用。McAlpine等[11]实验显示纯音噪声频率接近压力侧最大放大频率。Brooks 等[5]研究发现分离剪切层发展和层流转捩与翼型后缘产生的纯音噪声和宽带噪声直接相关。Pröbsting[5]等表明当层流边界层分离或者层流分离泡靠近翼型后缘,导致分离剪切层内强烈的相干扰动被放大产生纯音噪声。Brooks 和Hodgson 等[12]研究表明当层流分离泡靠近前缘,湍流边界层在后缘形成时,翼型后缘产生宽频噪声。由于层流到湍流的转变对各种自由流扰动具有固有的敏感性,因此这种噪声排放的发生将对翼型的流动发展产生显著的影响。Plogmann、Herrig 和 Würz[13]研究表明音调噪声的上游传播建立了一个声学反馈回路,从而影响了引起噪声排放的剪切层扰动的发展。Pröbsting 和Yarusevych[4]证明这种由吸力或压力侧事件决定的反馈循环可以改变LSB 特性。自20 世纪70 年代以来,越来越多的学者开始从事研究纯音噪声现象的工作,有人认为这可能与反馈回路机制有关。但是目前关于纯音噪声的生成机理还不明确,对声涡相互作用下分离泡内流动动力学特性还需要进一步研究。
格子Boltzmann 方法(lattice Boltzmann method,LBM)是一种介观动力学方法,在计算流体力学领域已经得到广泛应用,并逐步应用于声学研究[14-16]。Lew 等[17-18]采用LBM与大涡模拟(large-eddy simulation,LES)相结合的LBM-LES 方法,对高亚声速喷流噪声进行预测,表明LBM-LES 方法能够用于计算高雷诺数下湍流引起的宽频噪声。冯欢欢等[19]基于LBM-LES 方法对翼型纯音噪声数值模拟得到了较精确的结果。已有实验表明[7,20],中等雷诺数下,来流层流时,NACA0012 翼型声涡相互作用下的流动在翼型的展向方向上一致性非常高,可以将三维问题简化为二维,降低噪声直接计算的计算量。
因此本文基于LBM-LES 方法对中等雷诺数下NACA0012 二维翼型气动噪声进行直接计算,对声涡相互作用下边界层内流动的发展、流动特征及纯音噪声产生机理等进行分析。首先分析层流分离泡内扰动演化规律;然后研究边界层内纯音噪声的动力学压强脉动演化特征,最后对纯音噪声有关大尺度结构进行探讨。本文可为进一步认识声涡相互作用的机理、边界层流动稳定性及感受性等问题打下基础。
1 数值方法
1.1 LBM 方法
基于BGK 碰撞模型的标准格子Boltzmann 方程可以写成:
其中,fα为α(α=0,1,···,M)方向上的粒子分布函数;M为粒子碰撞方向的个数;为局部平衡分布函数;eα(eαx,eαy)为 粒子的离散速度;τ为松弛时间,可以用黏性系数 υ、温度T和时间步长δt来表示:
宏观物理量可以由式(3)求出:
其中,ρ为流体密度,u为 流体的速度,压力p可直接由理想气体状态方程p=ρc2得到,c为声速。
本文离散速度采用D2Q9 模型[21]:
其中,α1=1、2、3、4,α2=5、6、7、8。
平衡态分布函数为:
其中Wα为权系数。
1.2 LES 方法
大涡模拟基本思想是计算大尺度涡,而将小尺度涡对大尺度涡的影响用模型替代,并假定小尺度涡具有相似性。
对于翼型的非定常流动,动态Smagorinsky 亚格子模型在数值模拟翼型流动时,能很好地反映翼型边界层扰动变化的影响和翼型扰流的真实流动,可以捕捉到翼型后缘涡脱落纯音噪声的频谱特性[19]。本文采用动态Smagorinsky 亚格子模型来模拟小尺度涡对大尺度涡的影响。动态Smagorinsky 亚格子模型动力黏度 υ与松弛时间 τ的关系式为:
式中 υ0是分子黏度。将上式亚格子模型引入MRT(Multi-Relaxation Time)的LBM 方法(MRT-LBM)中,得到:
其中,Cs取 值为0.12,Δ 是 网格过滤的尺度,∂jui)为网格过滤后的应变张量。
1.3 网格分布与边界条件
计算域为40C× 40C,C为翼型弦长。在计算域内需要对流场和声场进行直接计算,属于多尺度问题,不适用一般均匀性网格,因此本文采用检索效率高的非均匀四叉树网格,并对计算域按照计算要求进行合理划分。主要分为四个不同网格密度的区域,分别为Level 1~Level 4,如图1 所示。最小网格尺寸Level 4 为 5.2 × 10-4C,满足壁面 Δy+量级为1,Δx+最大不超过5[22]。网格满足LES 方法近壁面区流动的直接求解要求,因此无需壁面函数。
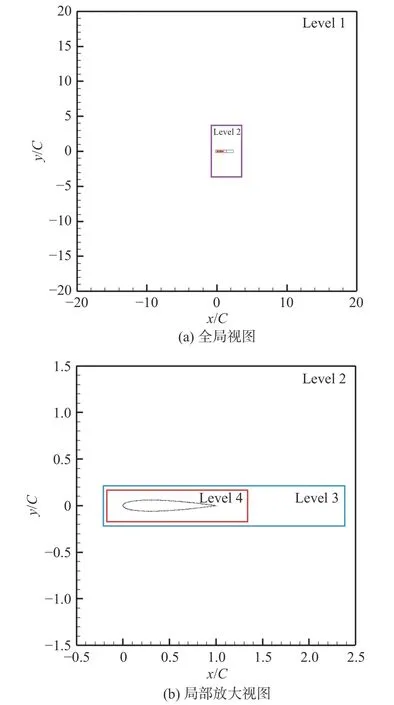
图1 NACA0012 翼型格子分布网格Fig.1 Grid distribution of the NACA0012 airfoil enlarged view
为了减小来自于边界并进入数值模拟区域的不必要的反射,采用局部一维无黏(LODI)方程推导出速度和压强的非反射 Dirichlet 边界条件[23]。本文计算采用的边界条件为:入口为速度边界条件;出口及上下边界为无反射边界条件。
2 计算结果与分析
2.1 数值方法验证
为验证本文数值计算的可靠性,采用LBM-LES方法对NACA0012 翼型在雷诺数为2 × 105(基于弦长C=0.3 m)、气体密度为0.350 8 kg/m³、采样频率为7 300 Hz、迎角2°条件下进行声场直接计算。从图2(a)中可看到,LBM-LES 方法得到的翼型吸力面时均压强系数与Mckee[24]实验值吻合得很好。图2(b)中,(1C,0.5C)处噪声的声压级(sound pressure level,SPL)频谱表现出明显的纯音噪声频谱特征,并与Desquesnes[20]采用的DNS 方法得到的主频幅值基本一致,变化趋势吻合良好。

图2 翼型吸力面时均压强系数分布和点(1C,0.5C)处声压级频谱图Fig.2 Mean pressure coefficient distribution on the suction side of the airfoil and SPL spectrum at the point (1C,0.5C)
图3 中远场声压与x=0.6C处近壁面和分离泡内动力学压强的功率谱密度(power spectral density,PSD)值比较发现,三者存在频率相同的峰值,说明远场纯音噪声和翼型分离泡内大尺度相干结构密切相关,并存在声涡相互作用,和实验结果[4]一致。

图3 边界层内压强及远场声压PSD 图Fig.3 PSD diagram of pressure in the boundary layer and sound pressure in the far field
2.2 流动时均特性
图4 为翼型时均流线图。从图4(a)中可以发现,在翼型吸力面剪切层流动分离后再附,存在明显的分离泡。分离泡中分离点S、转捩点T 和再附点R 如图4(b)所示。分离流线从壁面出发,最终回到壁面可以确定气流发生分离和时均再附的位置(即分离点S 和再附点R)。Kurelek 等[25]认为转捩点位于层流分离泡相对厚度最大位置,转捩点T 点位置为x/C=0.62。气流流经翼型壁面时,由于逆压梯度的作用,在S 点(x/C=0.42)开始发生气流分离;分离后的剪切层非常不稳定,会发生从层流到湍流的转捩,转捩后形成湍流,由于湍流可以将主流的动量引入剪切层,使得分离剪切层在R 点(x/C=0.68)再附到翼型壁面,从而形成分离泡。
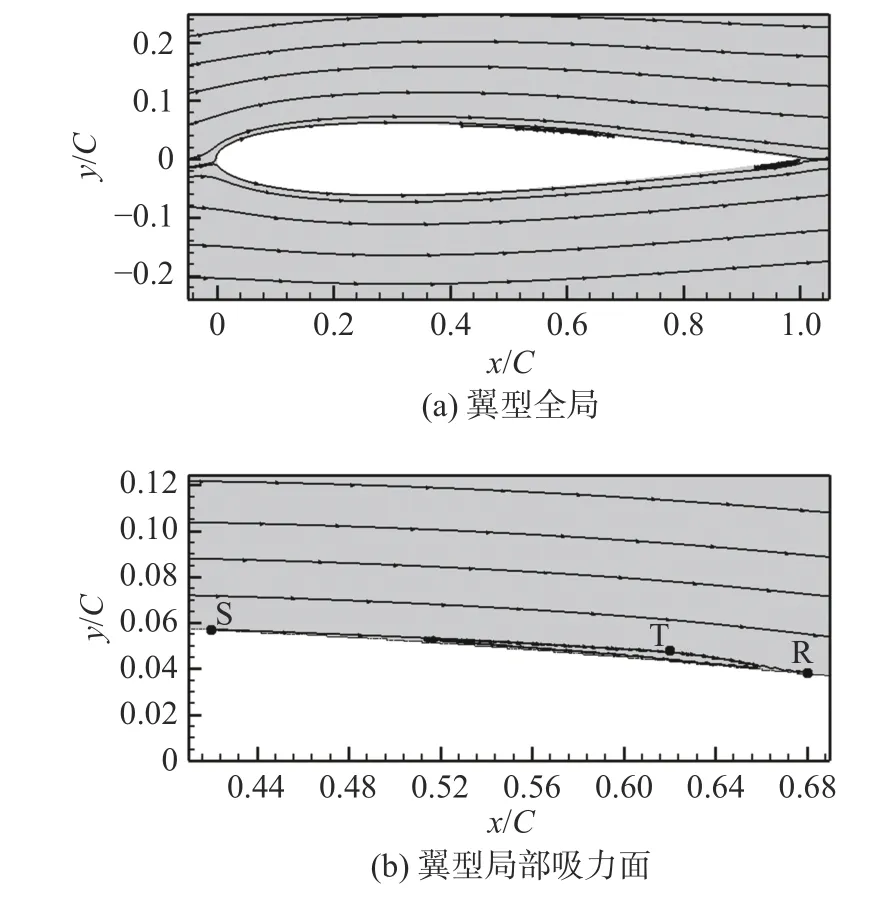
图4 翼型时均流线图Fig.4 Time averaged streamlines around the airfoil
图5 为翼型表面时均压强系数和吸力面边界层内时均湍流强度分布,Cp为表面压强系数,I为湍流强度。吸力面压强系数在S 点发生气流分离后,分离泡内部气流几乎静止,无法维持任何显著的压强梯度,使得吸力面压强系数几乎不变,曲线呈现平台特征;随后气流开始转捩成湍流,转捩过程中不稳定的气流可以加快剪切层内外动量互换,使得拐点T 点后压强迅速恢复,吸力面压强系数拐点与分离泡相对厚度最大的相对弦长位置一致,可以进一步说明T 点为转捩点,层流分离泡相对厚度最大位置和吸力面压强系数拐点可以用来判断分离泡内流动转捩位置。

图5 时均压强系数和时均湍流强度分布Fig.5 Distributions of the time averaged pressure coefficient and turbulence intensity
发生分离之前,湍流强度较小,边界层流动呈层流态;分离后,湍流强度快速增大直至分离剪切层转捩,转捩和再附之间,湍流强度保持不变;待分离剪切层再附后,湍流强度有所降低,可能是因为壁面黏性的作用。所以边界层分离后的自由剪切层对湍流强度的增长起重要作用,对远场气动噪声的影响可能非常关键,而附着剪切层内湍流强度的增长很小。
2.3 纯音噪声生成机理
图6 为翼型边界层内不同弦长处,750 Hz(纯音噪声频率)动力学压强的声压级(SPL)幅值,以观察边界层的发展过程。吸力面边界层在发生分离前,SPL 曲线平滑且缓慢增长;分离泡内,SPL 曲线开始出现波动,随后呈近似指数增长,直到分离剪切层再附达到最大值;再附后,SPL 值基于最大值呈现周期性发展。压力面观察到SPL 曲线在尾缘出现波动并迅速增长,在翼型尾缘和吸力面SPL 值相近,可能因为吸力面流动通过翼型后缘影响压力面的流动发展。从图6 中还可以发现,翼型边界层内近壁面和远壁面声压级沿着翼型分布几乎一致,说明在边界层内纯音噪声频率所对应的动力学压强脉动沿弦长分布特征,基本上与边界层内壁面法向位置无关;远场纯音噪声的产生是因为在自由剪切层里,动力学压强脉动(或扰动)迅速的增长。

图6 翼型边界层内750 Hz 压强声压级分布Fig.6 Distribution of pressure SPL at 750 Hz in the airfoil boundary layer
图7 为离散纯音频率(750、1 500、2 250 Hz)下的压强信号均方根(root mean square,RMS)值(幅值)沿着弦长分布图。750 Hz 频率压强信号的幅值在气流分离后先波浪式慢慢增长,分离后近似指数增长,而再附后指数增长结束开始呈现周期性波动,和图6 中规律一致;而750 Hz 信号的2 次(1 500 Hz)和3 次(2 250 Hz)高频谐波信号,呈现不同的发展规律。高次谐波信号幅值在分离剪切层流动转捩之后才开始增长,再附后继续增长到最大值,最大值相对弦长位置相同;频率越高,增长率越低。说明远场2 次和3 次谐波纯音噪声由同一物理机理生成的,和750 Hz纯音噪声生成机理不同。
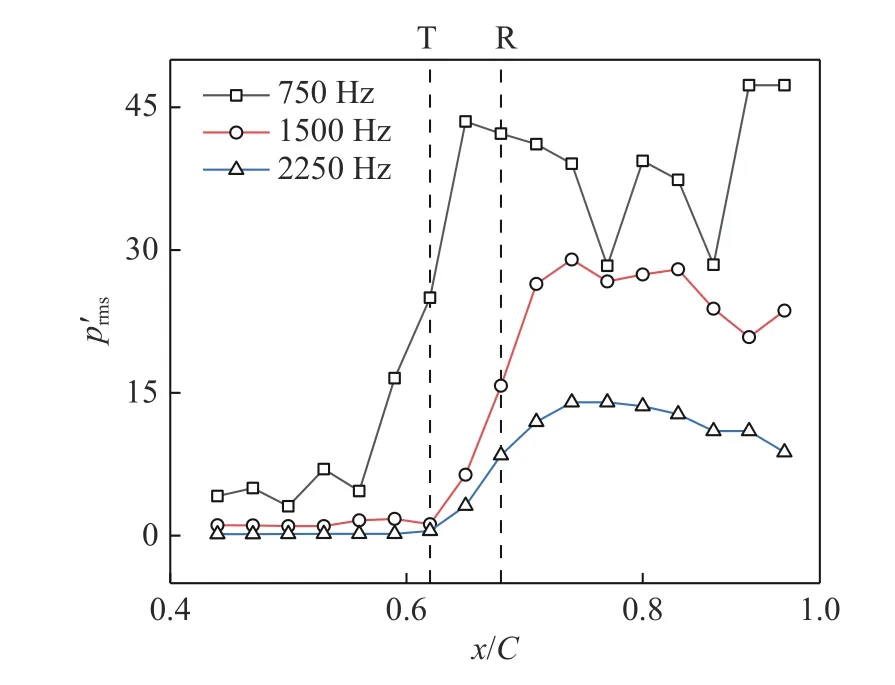
图7 翼型吸力面离散纯音压强脉动均方根分布Fig.7 RMS distribution of the discrete tonal pressure fluctuation on the suction side of the airfoil
2.4 边界层内流动的发展
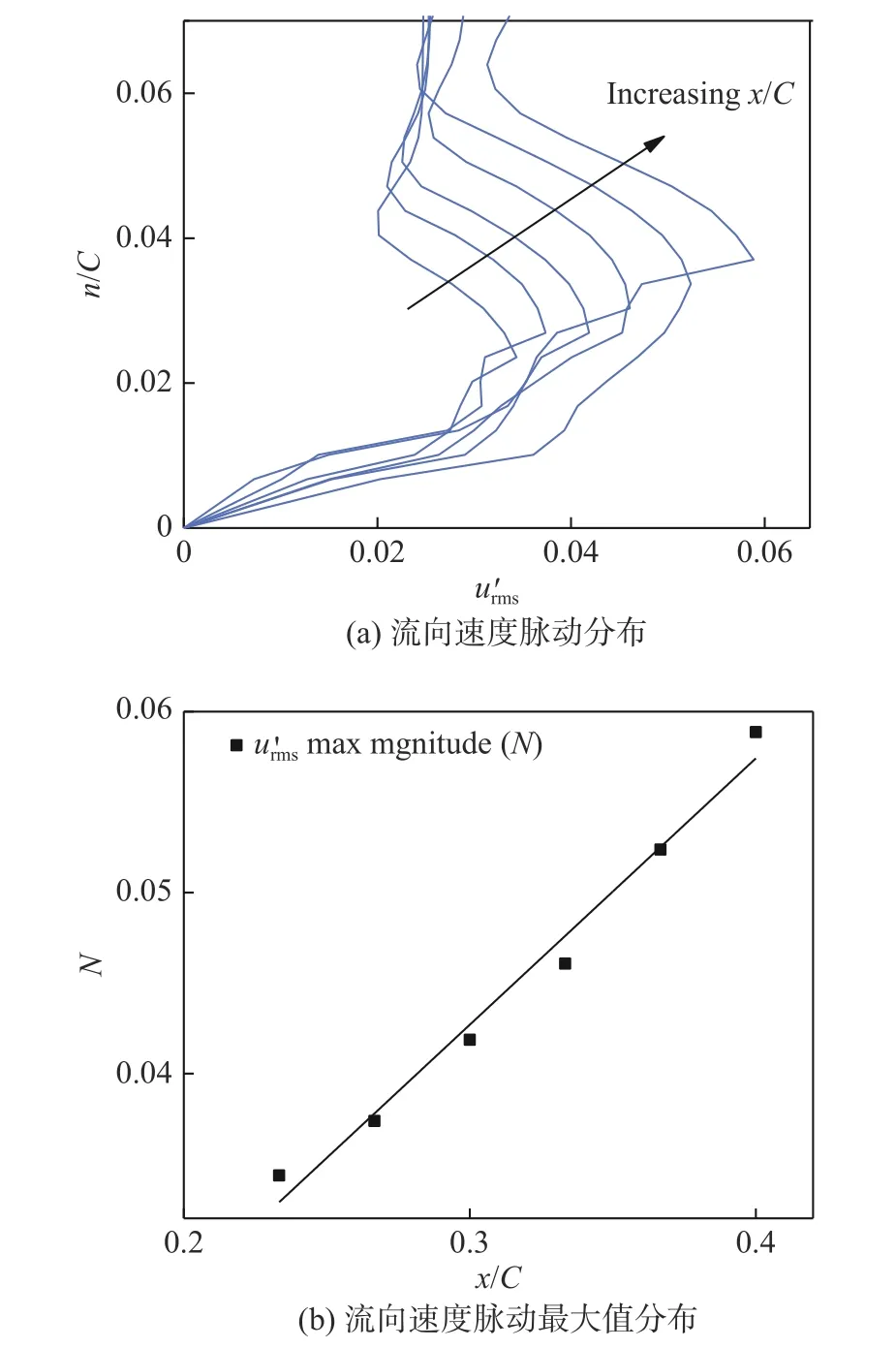
图8 分离前边界层流向速度脉动均方根Fig.8 RMS of the streamwise velocity fluctuation in the boundary layer before separation
图10 给出了流动边界层内的扰动从分离前到分离后的发展过程。分离前(0.41C处),沿壁面法向的分布呈现类高斯分布;发生分离后(0.44C处),沿壁面法向分布的形态发生了明显的变化,说明分离点在0.41C~0.44C之间,和时均流线及压强系数分布对分离点的预测结果相符。分离后,不再呈现类高斯分布,先是双峰分布,然后发展到三峰值分布,再附后又呈双峰值分布,如图9 所示。沿着壁面法线方向,扰动先增长到最大值,在有所减小后开始增长到峰值,随后减小直至边界层外缘。
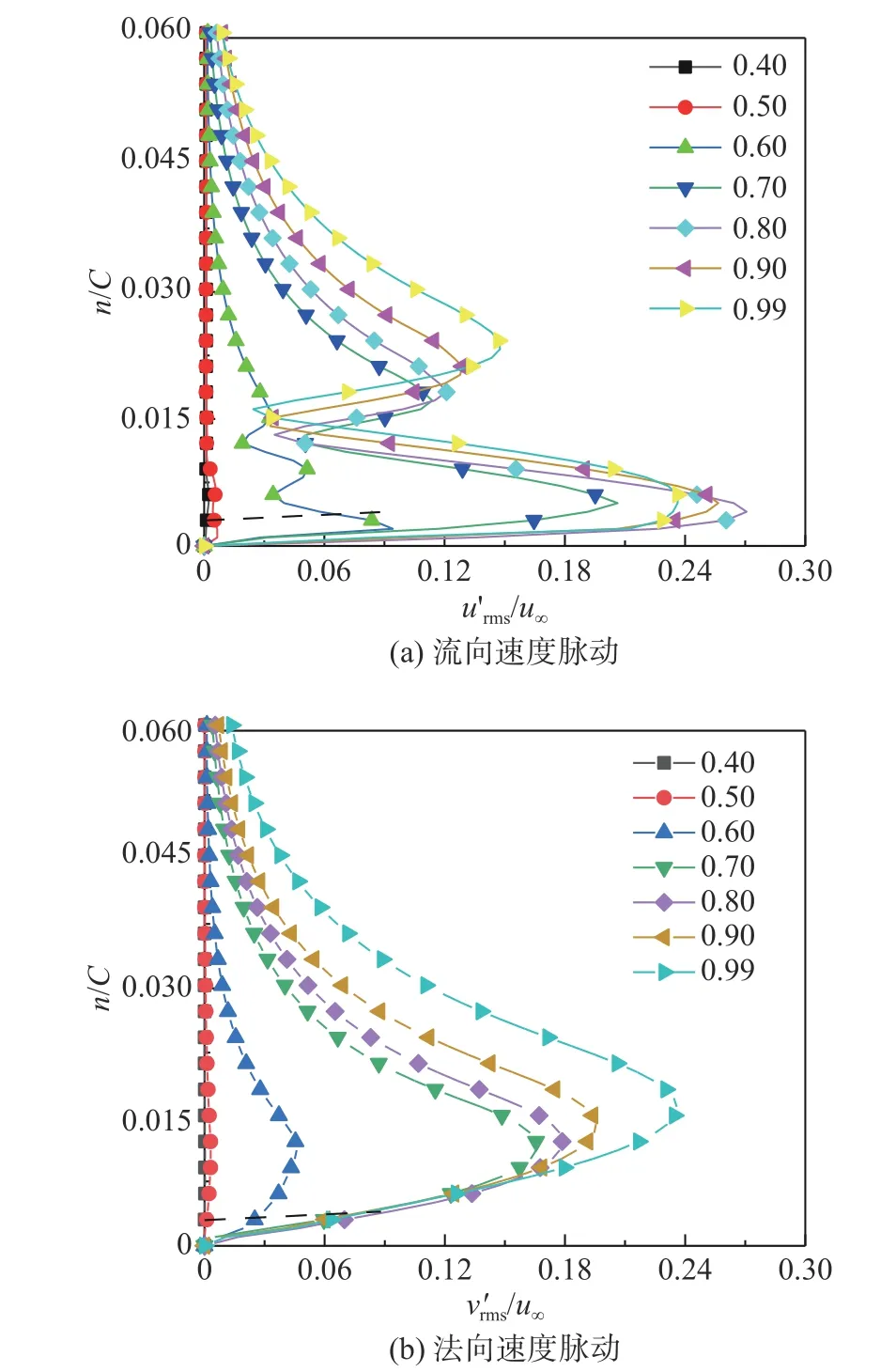
图9 分离后边界层内脉动分布Fig.9 fluctuation distribution in the boundary layer after separation

图10 流动分离前后流向速度脉动分布Fig.10 Streamwise velocity fluctuation distributions before and after the flow separation

图11 0.6C 边界层内速度及脉动均方根分布Fig.11 Distributions of the velocity and fluctuation RMS in the boundary layer at 0.6C
2.5 分离泡内大尺度旋涡结构
图12(a)显示了不同时间分离泡内涡量的分布,虚线表示了同一旋涡在不同时间的位置分布;从虚线的斜率可以看出再附前旋涡具有相同的对流速度0.598u∞,再附后旋涡对流速度变大。
在剪切层离开壁面后,大概0.55C处形成了较大尺度的旋涡,然后在再附点附近发展成稳定的旋涡结构,说明旋涡是从分离剪切层形成的,然后在分离泡内发展成稳定的结构。比较图9 中的不同位置流向速度脉动发展,发现在形成稳定的旋涡结构后,流向速度脉动沿着流向变化不大;稳定旋涡结构形成的过程,就是流向速度脉动增长最快的阶段。
在0.65C处壁面压强系数一个周期内的波形如图12(b)所示。旋涡经过0.65C时,该时刻压强系数为最小,旋涡离开后压强系数变大,旋涡运动的周期和压强系数波形图的周期一致,其频率都等于纯音噪声主频750 Hz。这进一步说明750 Hz 纯音噪声的生成是因为剪切分离流动失稳后,形成了较大尺度含能较高的旋涡结构。
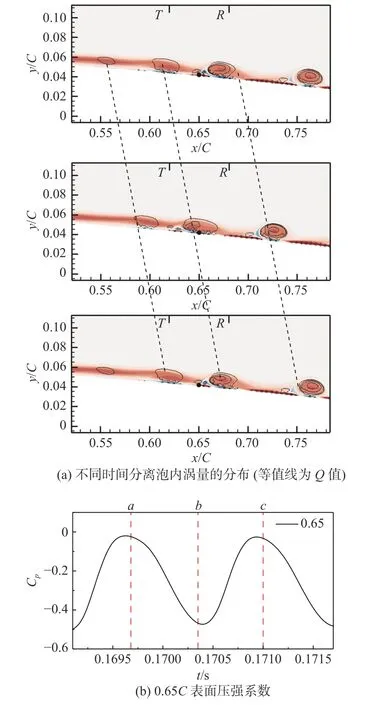
图12 不同时间分离泡内涡量的分布(等值线为Q 值)和0.65C 表面压力系数Fig.12 Vorticity distribution in the separation bubbles at different time instances (contour lines are for Q values) and pressure coefficient
分离泡内不同弦长位置归一化后壁面压强系数随时间变化的规律如图13 所示,从虚线可以看出影响压强信号的大尺度旋涡结构具有相同的对流速度,所以大尺度旋涡结构应为同一旋涡沿着流向发展而来的。在0.56C处,750 Hz 的旋涡结构已经形成,到0.62C处(再附之前)旋涡发展成稳定的旋涡结构。在分离自由剪切层再附后(0.68C处),压强信号出现高频信息;顺流向发展,高频信号表现得更加明显,但幅值比750 Hz 信号的幅值小很多。所以流动分离后,边界层的发展是由750 Hz 的大尺度周期性相干结构主导的。750 Hz 的高次谐波压强信号对应的旋涡结构,是在流动转捩后出现的,在分离剪切层再附后对边界层流动产生影响。

图13 分离泡内归一化压强波形图Fig.13 Normalized pressure waveform in the separation bubble
3 结论
本文基于LBM-LES 方法对NACA0012 翼型在雷诺数 2×105、2°迎角条件下的噪声声场进行了直接计算和验证,得出以下结论:
1)在翼型吸力面中段附近存在较长的分离泡,剪切层分离后,湍流强度显著增长直至转捩成湍流,但流动再附后,湍流强度有所降低;分离后的自由剪切层对远场纯音气动噪声的产生非常关键。
2)分离前流向速度脉动沿壁面法向的分布呈现单峰类高斯分布,分离后先是双峰分布,然后发展到三峰值分布,再附后又呈双峰值分布;边界层中流向最大扰动和分离泡中的逆向流动有关,K-H 不稳定对扰动的增长起重要作用。
3)自由剪切层K-H 失稳后,形成了纯音噪声频率750 Hz 的大尺度旋涡结构,该旋涡沿着流向发展,在流动转捩后但在再附前形成稳定的结构。主纯音噪声频率的2 次和3 次谐波频率对应的旋涡结构,是在流动转捩后产生的,在流动再附后继续发展成稳定旋涡结构。说明远场2 次和3 次谐波纯音噪声是由同一流动机理生成的,和750 Hz 纯音噪声生成机理不同。
本研究主要局限于翼型纯音噪声主频为750 Hz时附面层内分离泡的流动动力学特征分析,纯音噪声主频对动力学特征的影响、边界层内稳定性详细分析及感受性问题将是接下来要进一步研究的重点。此外,机翼实际会存在三维展向流动及翼尖涡,这使得翼型绕流的有效迎角和有效雷诺数发生变化,在一定程度上会对纯音噪声的频率和幅值产生影响,如何影响是值得深入研究又令人感兴趣的问题。
