宽包线吸气式高超声速飞行器外形优化研究

王健磊，牟 桓，魏 震，王 强，龚春林，*

(1.西北工业大学 航天学院，陕西省空天飞行器设计重点实验室，西安 710072；2.北京机电工程研究所，北京 100074)

0 引言

高超声速飞行器的动力系统一般采用吸气式发动机或组合推进系统。与传统的化学火箭相比，吸气式发动机以大气中的氧作为氧化剂，大大降低了飞行器的重量[1]。吸气式高超声速飞行器具有飞行速域宽、比冲高、推重比大等优点，目前适用的动力系统主要有火箭基组合循环动力系统（rocket based combined cycle,RBCC）[2]、涡轮基组合循环动力系统（turbo based combined cycle,TBCC）[3]、空气涡轮火箭发动机（air turbo rocket,ATR）[4]、涡轮辅助火箭增强冲压组合循环发动机（turbo-aided rocket-augmented ram-jet combined cycle engine,TRRE）[5]等。组合动力系统将不同的动力模态有机组合在一起并将彼此的优势结合，拓展了飞行器的飞行速域与空域[6]。

在吸气式宽包线高超声速飞行器设计所涉及的学科中，气动设计能够直接影响飞行器的飞行性能和飞行品质，对飞行安全、飞行效率与经济性等都具有决定性的影响。为了使飞行器具有良好的气动特性，气动外形优化是高超声速飞行器设计中面临的关键问题之一，国内外在该方面做了大量的研究。在国外，Takahiro 和Takeshi[7]对两级入轨RBCC 运载器进行了多学科优化设计，在气动模块上通过工程估算法来计算样本点气动特性并建立了RBF 代理模型，最后利用模拟退火算法来获取全局最优外形；Atsushi 等[8]基于三维Euler 方程以及序列二次规划算法对巡航点处的高超声速飞行器外形进行了优化，优化时将亚声速、跨声速两个设计点的气动性能作为约束条件，同时也考虑了防热、结构等其他学科约束，得到了较为理想的构型；Ahuja 和Hartfield[9]通过高速面元法求解巡航时高超声速飞行器的气动特性并利用准一维流来模拟发动机内流，实现了气动、推进、结构学科的匹配优化。在国内，车竞[10]以吸气式高超声速巡航飞行器为研究对象，利用多目标遗传算法，以巡航飞行阶段的气动力、气动热、雷达散射截面等作为优化目标，对高超声速飞行器气动布局的机身与机翼分别进行单独优化和总体优化；李晓宇[11]等对吸气式高超声速飞行器进行参数化建模，采用高精度CFD 方法建立了气动响应面近似模型，并结合遗传算法获得了不同优化目标的优化外形；陈兵[12]总结了吸气式高超声速飞行器的一体化设计与分析方法，运用多点优化的手段对宽速域RBCC 运载器的外形进行了分部件优化与整机优化，最后通过弹道验证证明了优化方案的优越性，但在整机优化时未使用基于N-S 方程的三维CFD 分析。综上所述，国内外对于吸气式宽包线高超声速飞行器气动优化设计研究目前主要集中在分部件优化与机体/推进一体化设计；在气动分析手段上，飞行器全机优化往往采用工程估算法，一定程度上影响了优化结果的可靠性；在评估点选取上，以单点优化为主，满足不了工程实际的需要；在优化策略上，以全局或局部范围内的单轮优化为主，无法保证优化结果的全局最优性。因此对于吸气式宽包线高超声速飞行器，基于三维高精度CFD 手段且考虑多评估点的多层气动优化仍需要进一步研究。

针对本文的优化问题，确立了如图1 所示的包含基于自适应代理模型的全局优化和基于伴随梯度法的局部优化的两层优化思路。宽包线气动优化问题往往是非线性、多峰值的，使用梯度算法容易陷入局部最优。使用代理模型来代替真实模型可以减少需要计算的样本点数目，但代理模型需要大量的样本点训练才能达到较高的精度，这对于本文的气动优化问题来说仍是不可承受的。因此，本文提出一个折中方案：首先利用略低于平均精度水平的代理模型得到初步优化方案，在此基础上通过梯度算法进行局部寻优。第一步优化代理模型的精度不需要太高，这样能有效减少训练样本点的数目。第二步优化求解目标函数与设计变量的梯度时采用了离散伴随方法，该方法的计算量与设计变量个数无关，可大大提高梯度求解效率[13-14]。因此，该优化策略既能有效降低气动计算量，又能得到相对精确的优化解。

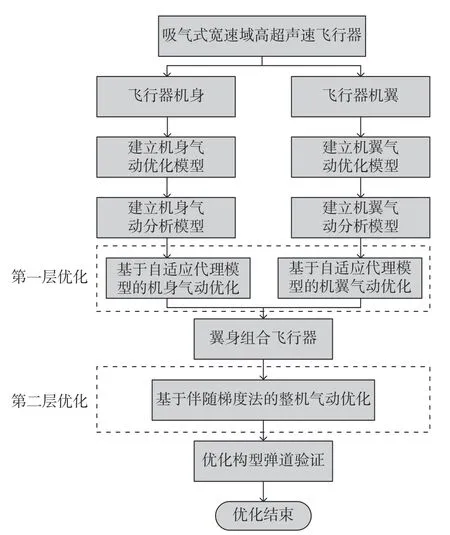
图1 基于翼身分解的分层优化思路Fig.1 Multi-layer optimization idea based on wing body decomposition

1 飞行任务描述

本文研究的对象是水平起降的宽包线高超声速飞行器，其动力系统采用RBCC 组合动力发动机。飞行器的典型飞行任务剖面如图2 所示。整个任务的飞行速域范围Ma=0～8，高度范围H=0～50 km。

图2 飞行任务剖面Fig.2 Flight mission profile

2 优化问题描述

2.1 问题提出

2.1.1 机身优化目标

本文采用加权求和法对优化结果进行评估。将阻力系数作为本文的优化目标，即：

其中，X为飞行器的外形优化设计变量，J为优化问题的目标函数。

对一定量的评估点的目标函数按式（2）进行标准化处理，Ji为第i个评估点的目标函数值，为样本中的目标近似最小值，为近似最大值：

最后得到的优化目标函数为：

其中：Jbody为 总的优化目标函数，N为优化评估点数目，ωi为 权重因子，为每个评估点标准化处理后的目标函数值。

将马赫数1.2、2.5、5.5、8.0 作为气动优化评估点。权重系数选取以基准弹道为参考，各评估点的权重系数为燃料消耗对阻力系数的偏导数。考虑到实际弹道的结果数据往往以离散的形式给出，各评估点的权重系数可表示为：

其中，ωi为权重因子；mF为燃料质量；CDb为阻力系数；ΔmF,i为第i个评估点下飞行器燃料消耗，是阻力系数的函数。通过式（4）可以看出如果在某个优化评估点阻力系数变化对燃料质量变化的影响越大，则这个计算点在多目标向单目标转化中所获得的权重也越大。最终获得的权重系数如表1 所示。

表1 机身优化评估点权重系数Table 1 Weight coefficients of the airframe optimization evaluation points

2.1.2 机翼优化目标

机翼优化设计同样需要采用多点优化方法，式（5）为其优化目标。但与机身不同的是，机翼需要承担飞行器起飞时绝大部分的升力，因此需要将计算起飞时Ma=0.4 的点作为优化分析点：

其中Jwing为机翼的优化目标函数。

参考基准弹道，最终得到机翼优化的评估点与权重如表2 所示。

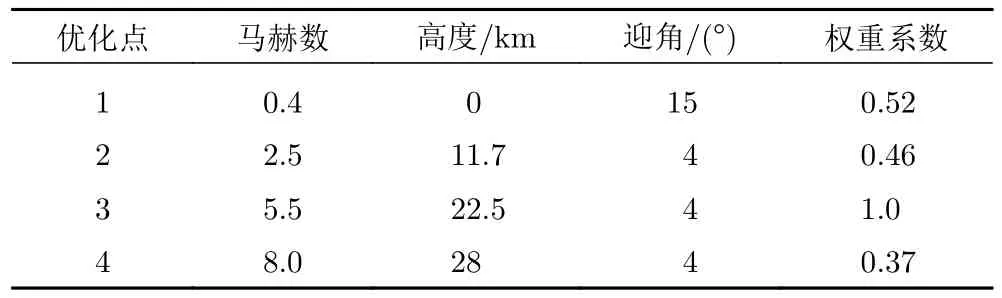
表2 机翼优化评估点计算状态与权重Table 2 Computational conditions and weights for the wing optimization evaluation points

2.2 优化约束

表3 为机身优化问题的主要约束变量和范围。变量范围均根据工程估算给出；其中为焦点相对位置，假定飞行器机身的质心相对位置为0.6。机翼优化问题的约束变量和范围如表4 所示。

表3 机身约束变量及约束范围Table 3 Airframe constraint variables and ranges

表4 机翼约束变量及约束范围Table 4 Wing constraint variables and ranges

3 飞行器气动分析建模

3.1 物理模型

飞行器基准构型采用翼身组合体的气动布局形式（图3），全长约32 m，最大翼展约19 m，进气面积10 m2，起飞质量约130 t。

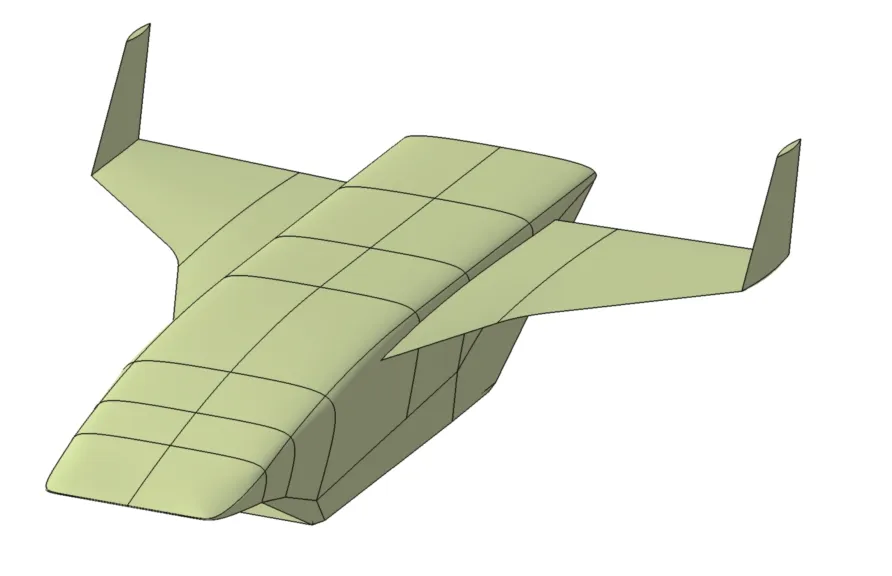
图3 吸气式高超声速飞行器基准外形Fig.3 Basic shape of the air-breathing hypersonic vehicle

机身参数化建模采用模线设计法，即通过构造飞行器不同位置的几个截面形状和每个截面的轮廓曲线来描述飞行器外形。如图4 沿飞行器纵轴设置5 个截面并对截面上的轮廓曲线进行参数化建模（图5），在二次曲线上选择一个控制点，则每个截面只用hi和 θi两个变量就能表示。其中：ai为z=0 对称面机身上表面轮廓线到下表面的距离；w为发动机宽度Wengine的一半；hi和 θi分别为各截面控制点的y坐标、轮廓的底部切线与x轴的夹角参数化；下标i为截面编号，取1～5 的整数。

图4 z=0 面上飞行器纵向轮廓及截面位置Fig.4 Longitudinal profile of the vehicle at z=0 and the cross-section positions

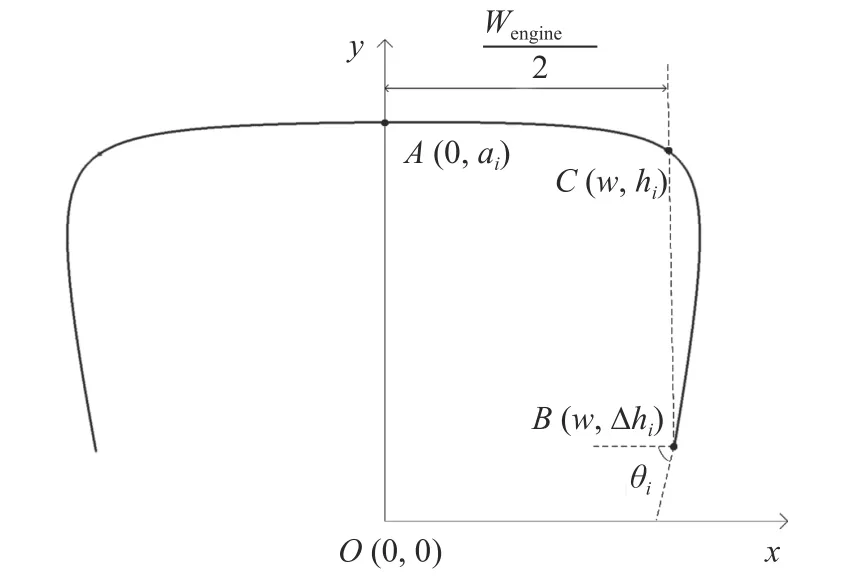
图5 飞行器机身截面轮廓和参数Fig.5 Cross-section profile and parameters of the vehicle fuselage

飞行器头部通过幂函数进行参数化设计，从y轴正方向向下俯视的轮廓曲线表达式为：

将n作为参数化变量，头部形状参数化示意图如图6 所示。最终完成的机身参数化模型三视图如图7所示。将发动机宽度作为参数化变量，进气高度可经计算得到。对于尾喷管，在入口高度一定的情况下，其长度是影响其气动特性的主要参数[15]，故取尾喷管长度作为设计变量。机身设计变量与范围如表5所示。

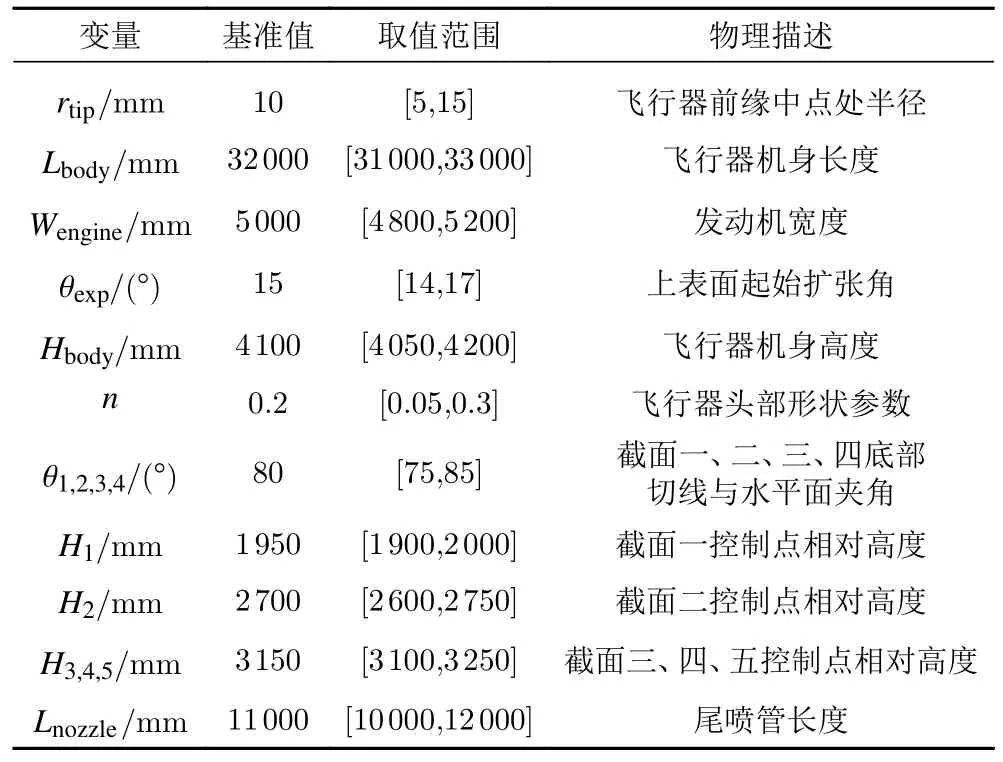
表5 机身设计变量与范围Table 5 Body design variables and ranges

图6 头部形状参数化示意图Fig.6 Schematic diagram of the parametric vehicle head

图7 机身参数化模型三视图Fig.7 Three views of the parametric fuselage model

水平机翼与垂尾组成的机翼建模如图8 所示。机翼的设计变量与范围如表6 所示。

表6 机翼设计变量与范围Table 6 Wing design variables and ranges

图8 机翼参数化建模Fig.8 Parametric modeling of the wings

3.2 气动特性计算模型

本文按照算力界面将整个流场划分为发动机内、外流场两部分，该划分方式对于绝大多数吸气式高超声速飞行器在宽包线范围内的研究有较好的适用性[16]。发动机内流场包括隔离段与燃烧室，采用准一维流计算，其他所有区域都定义为外流场，采用CFD 计算。本文的气动/推进算力界面划分如图9 所示，ABCD四点范围内划为推进学科，其余部分划为气动学科。

图9 气动/推进算力界面划分Fig.9 Aerodynamic/propulsion calculation interface division

4 基于分层优化的气动优化框架

基于提出的气动优化问题，本文构建面向具体问题的气动优化框架。为了保证优化精度和提高优化效率，本文在优化框架中设计了两层优化，如图10所示。

图10 气动优化框架流程图Fig.10 Flow chart of the aerodynamic optimization framework

第一层优化通过代理模型在全局范围内进行寻优，求解优化加点准则[17-18]定义的子优化问题，引入自适应加点提升全局搜索效率，本层的优化对象为单独的机身与机翼。当基于自适应代理模型的优化迭代一定次数后，继续加点对最优值附近的代理模型精度提升有限，此时可以在第一层优化的基础上进行第二层优化。第二层优化为局部优化，优化算法为最速下降法[19]，梯度信息可通过离散伴随法获得，该层的优化对象是翼身组合飞行器。

4.1 基于自适应Kriging 代理模型的第一层优化

4.1.1 自适应Kriging 代理模型的加点策略及改进

为了提高优化效率减少计算量，将Kriging 代理模型引入本文的优化问题[20-21]。基于代理模型直接优化仍然需要计算大量的样本，且盲目地在全局范围内加点会造成计算资源的浪费。为了提高优化效率，需采用一种快速高效的加点策略来研究本文的优化问题。Kriging 代理模型的加点准则有极值加点准则、EI 加点准则、误差最大加点准则等[22]，但每轮迭代只能加入一个新的样本点，导致优化效率较低，而并行加点法能在一轮内同时加入多个样本点，在计算资源充足的情况下，比单一加点法的优化效率更高，能极大地缩短优化所需的时间。

在所有的并行加点准则中，基于EI 准则的自适应加点手段应用最为广泛，但由于EI 准则存在固有缺陷，在全局最优值附近往往无法精确收敛。针对这个问题，本文提出的改进方法是将代理模型的预测最优值作为每步迭代的新增样本之一来改善搜索的局部收敛性。该方法本质上是极值加点准则与基于EI 准则的并行加点法的结合，在寻优前期EI 准则可以发挥其全局性，克服极值加点准则容易陷入局部收敛的缺陷；寻优后期全局最优解的范围大致确定，极值加点准则可以起到加速收敛的作用。

4.1.2 算例测试

为了检验离散伴随方法流程的有效性，应对其进行算例测试。本文采用翼型NACA0012 算例作为实际工程问题。该算例的来流状态为：总温T=311 K，总压p=101325 Pa，马赫数Ma=0.7，迎角α=1.55°。为了便于控制翼型形状，需要对其进行参数化处理，这里采用的参数化方法为CST 方法[23]。对NACA 圆头尖尾系列的翼型，规定翼型弦长为1 m，则CST 曲线的数学表达式为：

其中：ai为控制参数，n为Bernstein 多项式次数，=n!/[i!(n-i)!]，ΔyTE为翼型后缘厚度。算例采用6阶Bernstein 多项式，翼型上下表面的形状均由7 个参数控制，设计变量共14 个，其区间设置可参考文献[24]。

本文在保证升力不下降的同时对翼型进行减阻设计，从而进一步提高翼型在设计点的性能。该优化问题可表述为：

其中：CDa为翼型的阻力系数，CLa为优化后翼型的升力系数，CLa1为优化前翼型的升力系数。

采用序列二次规划法（NLPQL）作为该算例的优化算法，其他优化条件保持不变。为了验证本文离散伴随法的计算精度，利用有限差分法与离散伴随方法分别求解初始翼型阻力系数对外形参数的梯度并将计算结果进行对比，两种方法的扰动步长均设为0.001。表7 给出了两种方法的梯度计算结果，由表可知14 个外形参数的最大差别仅为3.34%，因此可认为伴随梯度方法的计算结果可靠，可用于之后的气动优化。

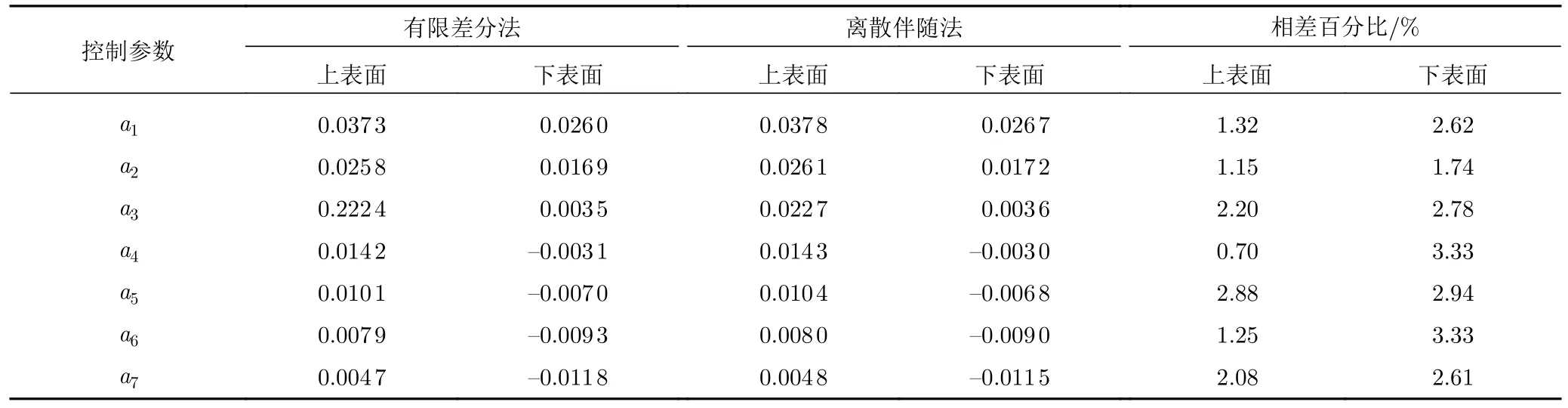
表7 两种方法的梯度计算结果对比Table 7 Comparison of the gradient calculation results between the two methods

下面通过算例来测试改进方法的有效性。本文主要考虑三种并行加点方法：混合加点法、Kriging 信任法、多点EI 法，其中混合加点法是在每步迭代时分别基于4.1.1 节中所提到的三种单一加点准则进行加点；Kriging 信任法为基于EI 准则的经典并行加点法，详见文献[25]；多点EI 法由文献[26]提出，是一种较为高效的并行加点方法。对于以下算例，所有并行加点法每次迭代均增加3 个新样本点，改进的加点策略每步迭代基于原方法添加2 个新样本，基于极值加点准则添加1 个新样本。初始样本的训练方法均为拉丁超立方抽样，基于代理模型的全局寻优方法均采用遗传算法。

G9 函数是测试全局优化算法的经典算例[27]，共有7 个设计变量和4 个约束，由于其优化可行域小、收敛下降量级大，优化难度较高，可对本文的寻优策略进行很好的检验。

G9 函数的数学模型为：

其中xi∈[-10,10]，i=1,···,7。通过样本训练得到300 个点作为初始样本建立Kriging 代理模型，采用多种加点策略来提高代理模型的近似精度。各自适应加点策略的收敛流程如图11 所示，优化结果与调用函数模型的次数如表8 所示。

图11 G9 算例各种自适应加点策略的收敛流程Fig.11 Convergence process of various adaptive point addition strategies for the G9 case

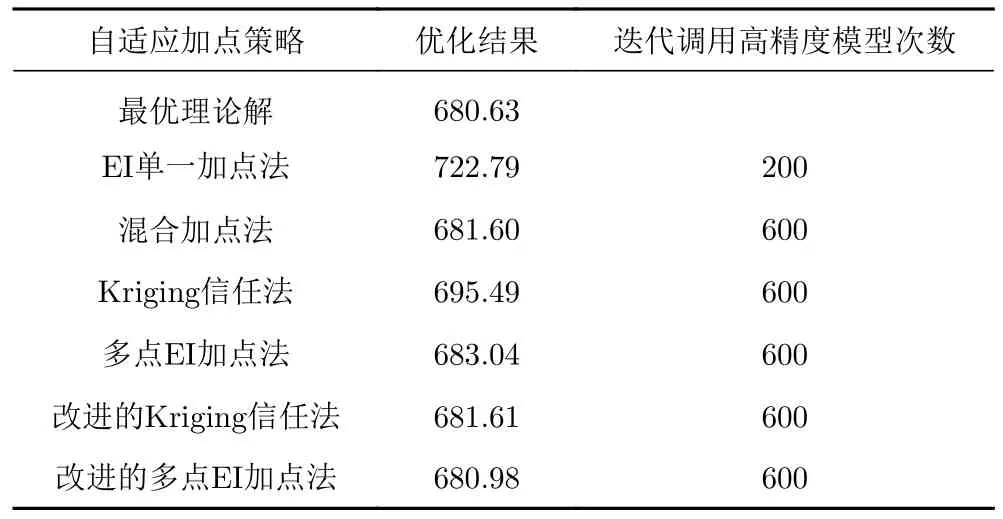
表8 G9 函数优化结果及调用高精度模型次数对比Table 8 Comparison of the G9 function optimization results and the times of calling high-precision models

根据不同并行加点策略之间的对比，可以发现对于复杂函数，在调用同样次数高精度模型的条件下，改进后的两种方法相比于改进前在收敛速度和结果精度上都有了较大的提高，说明本文提出的改进措施是有效的。多点EI 加点法改进后的优化效率提升更大，是本文研究的几种并行加点法中最优的加点策略，因此本文采用改进后的多点EI 法来解决之前提出的优化问题。

4.2 基于离散伴随法的第二层优化

为了在第一层优化的基础上获得整体气动性能更优的方案，需进一步采用梯度算法局部寻优。本文将离散伴随方法引入优化过程以降低求解梯度时的气动计算量，建立了基于伴随梯度法的气动优化流程如图12 所示[28]。

图12 基于离散伴随方法的优化流程图Fig.12 Flow chart of the optimization process based on the discrete adjoint method

5 优化结果

5.1 第一层优化结果

表9 给出了机身外形优化结果，该外形与基准外形的对比如图13 所示。图14 和图15 分别给出了马赫数5.5 时基准外形与优化外形在对称面处的静压与马赫数云图。由以上结果可知相比于基准外形，考虑所有约束的机身优化外形整体尺寸略有缩小、减阻效果显著，而且静稳定性、容积率、发动机进气条件三项指标也均有了明显的提升。

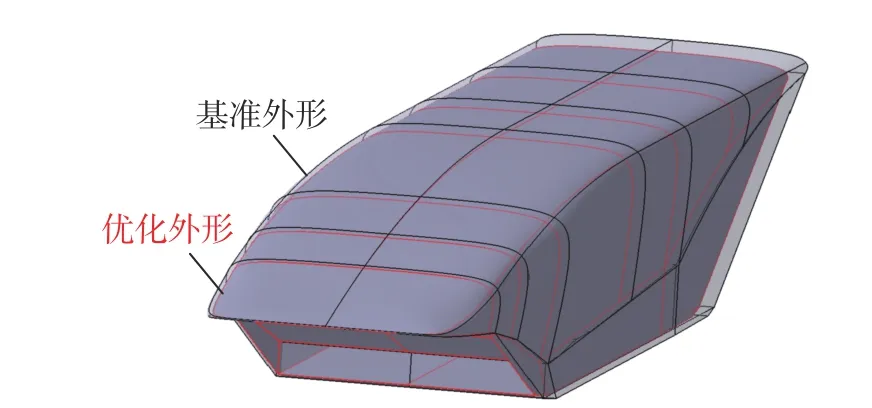
图13 机身优化外形与基准外形对比Fig.13 Comparison between the optimized and reference fuselage shapes

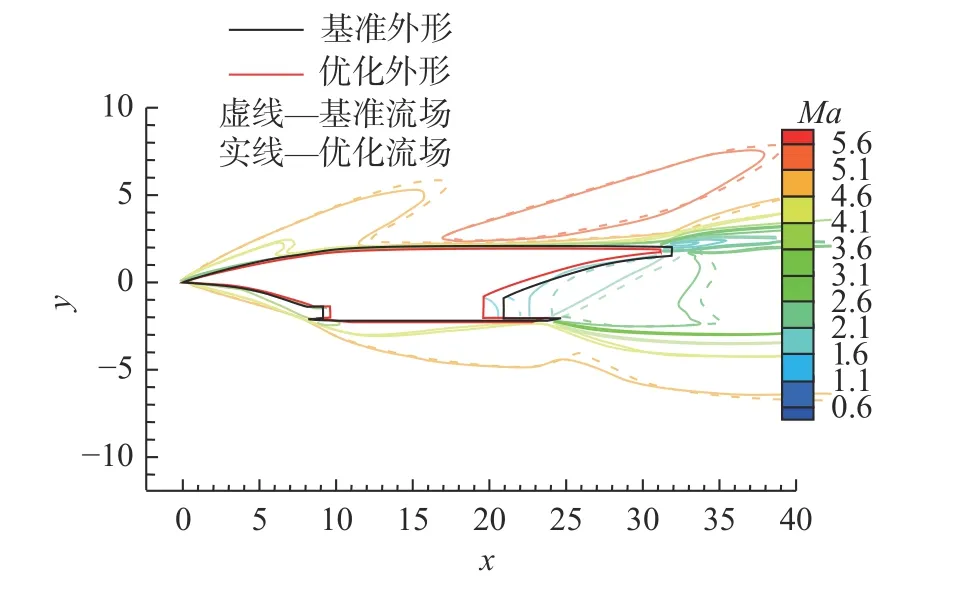
图15 Ma=5.5 时机身对称面处的马赫数对比Fig.15 Comparison of Mach number in the symmetry plane of the fuselage at Ma=5.5

表9 机身第一层优化结果Table 9 First layer optimization results of the fuselage

机翼最终的优化结果如表10 所示，该外形与基准构型的对比如图16 所示，可以看出优化外形的水平机翼面积缩小，垂尾弦长增加但高度减小。图17和图18 分别给出了马赫数5.5 时机翼基准外形与优化外形在下表面的静压云图和对称面的马赫数云图。马赫数5.5 时机翼半展长处的压强如图19 所示，可以看出优化后机翼前缘压强显著降低，减阻效果明显。

图16 机翼基准外形与优化外形对比Fig.16 Comparison between the baseline and the optimized shape of the wing

图17 Ma=5.5 时机翼下表面的静压对比Fig.17 Comparison of static pressure on the lower surface of the wing at Ma=5.5

图18 Ma=5.5 时机翼对称面处的马赫数对比Fig.18 Comparison of Mach number in the symmetry plane of the wing at Ma=5.5

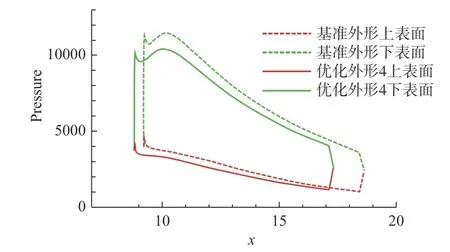
图19 Ma =5.5 时机翼半展长处上下表面压强对比Fig.19 Comparison of pressure on the upper and lower surfaces of the wing at half-wingspan for Ma=5.5

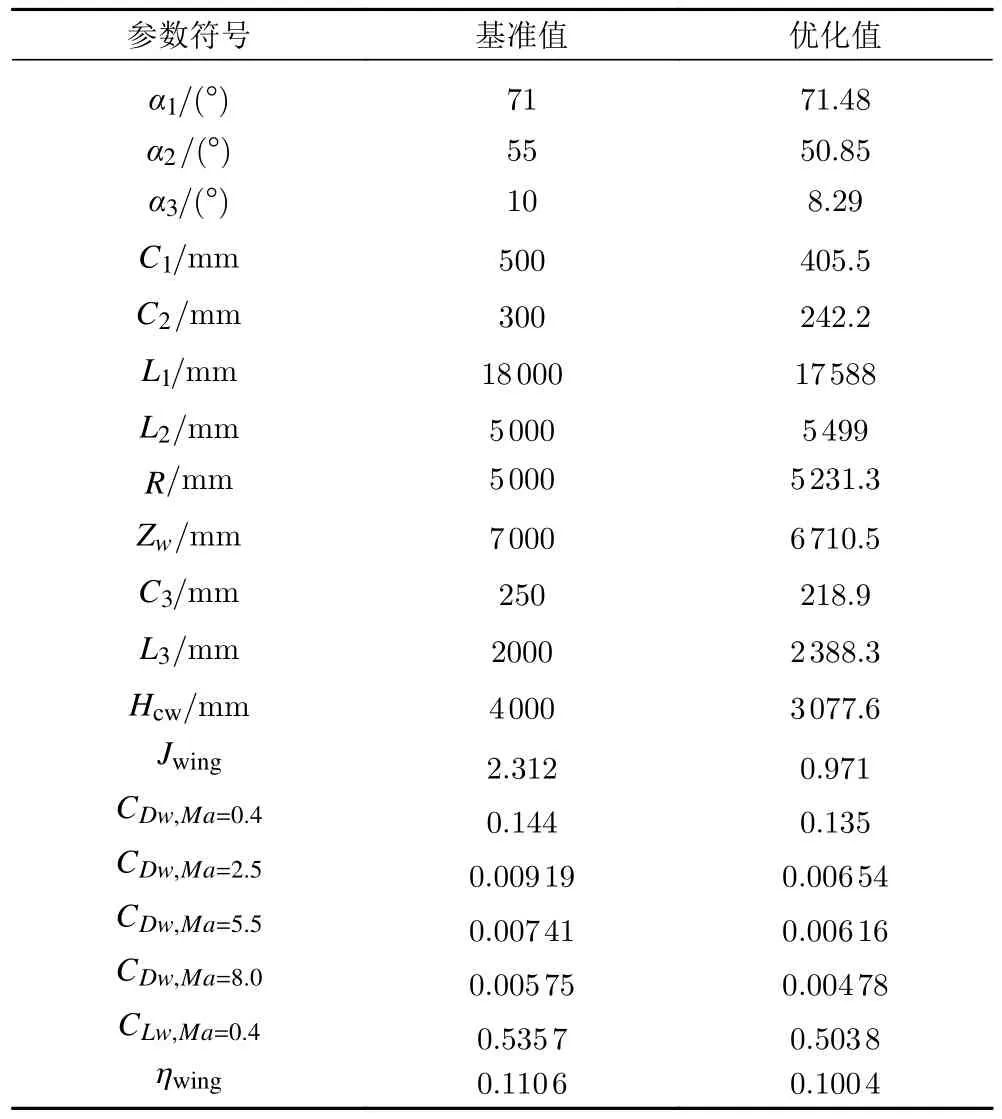
表10 机翼外形优化结果Table 10 Wing shape optimization results

5.2 第二层优化结果

该层优化的目标函数与机身、机翼的优化目标形式相同，记为Jcom。优化评估点和权重选择表1 中的4 个典型特征点及其相应权重，优化约束为机身、机翼优化问题的约束集合。翼身组合体的设计变量包括了机身、机翼优化问题的设计变量以及描述翼身相对位置的两个新变量，共24 个外形参数。新增的两个外形参数的详细描述如图20 所示。翼身组合体优化前后的各项参数如表11 所示，优化前后的外形对比如图21 所示，可以看到两者外形较为近似，伴随优化外形的整体尺寸略有缩小，4 个气动评估点的阻力系数均有所降低，目标函数比优化前减小了19.6%。图22 和图23 分别给出了马赫数5.5 时第一层优化结果与伴随优化外形在对称面处的静压与马赫数云图，从图中可以看出相比于第一层优化的外形，伴随优化外形的前缘高压区面积略微减小，后缘高压区面积略有增大，在满足约束的前提下使阻力进一步降低。

图20 新增两个设计变量的图形描述Fig.20 Schematic description of the two new design variables

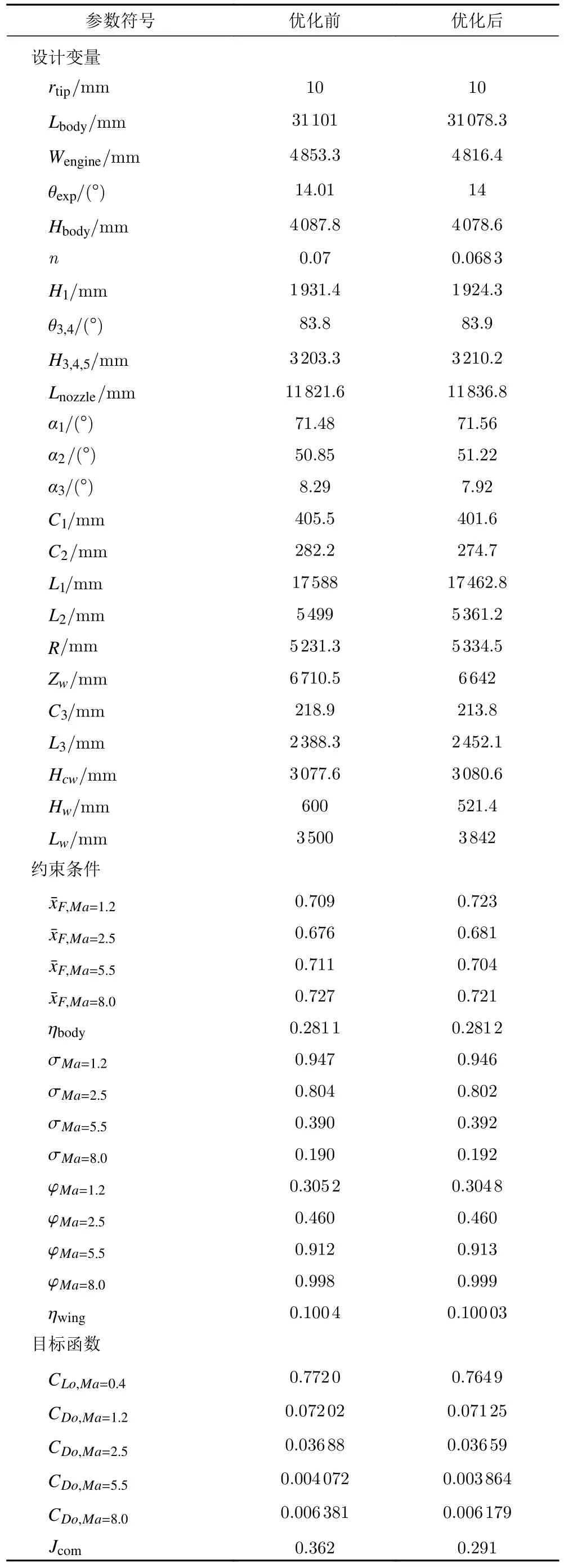
表11 翼身组合体优化前后参数对比Table 11 Comparison of parameters before and after optimization of the wing body assembly

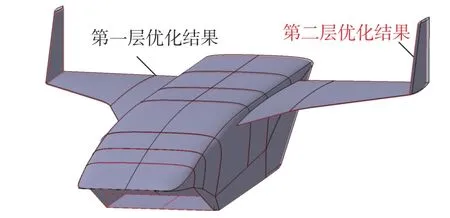
图21 第二层优化后的飞行器外形Fig.21 Vehicle shape after the second layer optimization

图22 Ma =5.5 时两层优化结果在对称面处的静压对比Fig.22 Comparison of static pressure in the symmetry plane for two-layer optimization at Ma =5.5

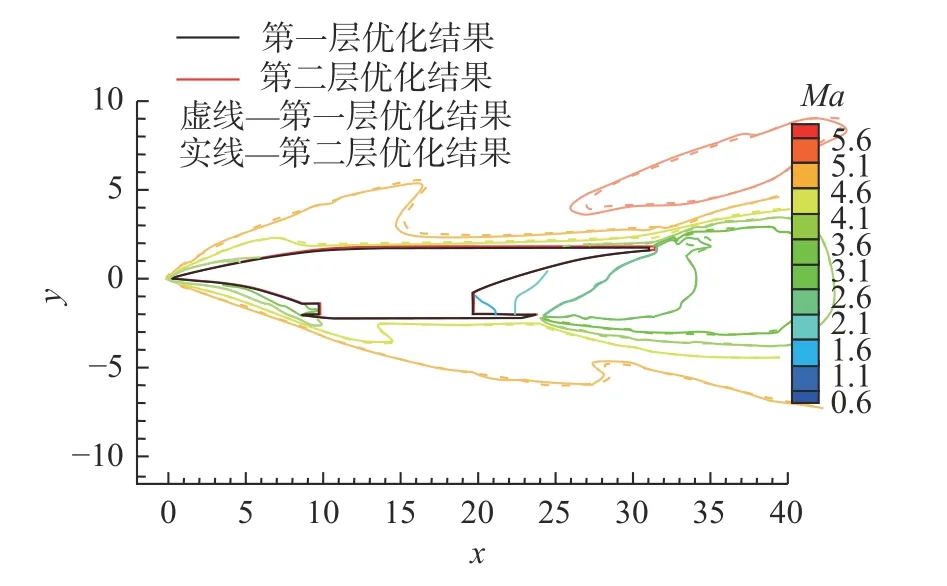
图23 Ma=5.5 时两层优化结果在对称面处的马赫数对比Fig.23 Comparison of Mach number in the symmetry plane for two-layer optimization at Ma =5.5

6 结论

本文以两级入轨飞行器中的下面级—吸气式高超声速运载器为研究对象，基于翼身分解的思路构建了多评估点的气动优化模型；建立了飞行器的气动分析模型，对算力界面进行划分并使用“CFD+准一维流”的气动求解流程；提出了基于分层优化的气动优化方法并对改进的自适应Kriging 代理模型加点策略进行算例测试，证明了改进措施的有效性；最后通过搭建的优化框架对吸气式高超声速飞行器的气动外形进行了分层优化。

1）针对本文算例模型，验证了根据燃料消耗对阻力系数的偏导数给出多优化评估点的权重系数的方法是可行的；

2）将代理模型的预测最优值作为每步迭代的新增样本之一的Kriging 代理模型的加点准则可以改善搜索的局部收敛性；

3）本文提出的优化方法在满足各学科约束的条件下可以使飞行器在4 个优化评估点处的阻力系数均有所减小。