基于GBDT 算法的混凝土叠合面黏结强度预测分析

王建民，叶钰蓉，饶超敏，卓仁杰，柳俊哲，3，*

（1.宁波大学 土木与环境工程学院，浙江 宁波 315211；2.电子科技大学 计算机科学与工程学院，四川 成都 611731；3.青岛农业大学 建筑工程学院，山东 青岛 266109）

普通混凝土（NC）与陶粒轻骨料混凝土（LWAC）之间的浇筑结合面（叠合面）为叠合构件的薄弱部位.叠合面的黏结强度受两侧混凝土材料性能、浇筑间隔时间、叠合面受力状态和叠合面处理方式等多种因素的综合影响.其中，浇筑间隔时间在较短时间范围内变化时影响较明显，且为非线性变化关系［1］.在低静水压力情况下，新老混凝土黏结强度与叠合面上法向作用力近似呈线性关系［2］.针对陶粒轻骨料混凝土和普通混凝土在较短时间间隔内的叠合浇筑，文献［3］在试验分析基础上提出具有内部分层式速度间断面的剪切破坏模型，将叠合浇筑的剪切破坏强度与剪切破坏面及破坏机构的形成、相关材料的特性相关联.考虑上述诸多因素及其相互之间的耦合影响，混凝土叠合面上的黏结强度影响表现为复杂关联的非线性关系.虽然可通过多参数分组组合，采用多因素多水平方法对叠合面黏结强度的变化影响开展试验分析，但有限的分组试验、试验数据的离散性等无法就各因素对黏结强度的变化和影响进行准确的预测分析.

BP 神经网络（BPNN）已广泛应用于优化混凝土配合比以及预测混凝土性能等方面，并取得了良好的预测效果［4-7］.但BPNN 作为一种单一学习器，在预测准确率上仍存在一定的局限，模型的可解释性不强，建模时神经元个数和隐含层层数等模型结构参数的选择尚无科学依据，需要从实践中总结经验.机器学习中的其他非线性模型，如随机森林（RF）、自适应提升（AdaBoost）、极端梯度提升（XGB）和梯度提升决策树（GBDT）等，是以决策树（DT）为基本模型的集成学习方法，可将单一学习模型有机结合，形成一个统一模型，从而可获得更准确可靠的预测学习结果.Tuan 等［8］采用XGB 学习方法根据混凝土材料组成和龄期对其立方体抗压强度进行了准确地预测分析.相比较而言，GBDT 作为一种成熟的集成学习算法，将多个回归树模型串联在一起，组成一个强学习器，其基本学习器回归树模型具有效率高、缺失值不明显的特点［9］，更注重学习模型的精度［10］，具有高效、预测准确、对原始数据不敏感和可解释性强等优点［11-12］.热镀力学性能学习模型的预测结果比较表明，GBDT、RF 和AdaBoost 这3 种集成学习模型在训练效率、预测精度以及在测试数据上的泛化能力优于BP 模型［13］.其中，GBDT 模型的预测精度和泛化能力最好.有关GBDT 在混凝土材料及其相关领域的预测分析目前尚未见研究和报道.

本文设计制作了多组陶粒轻骨料混凝土与普通混凝土叠合试块，对其进行了双面直剪试验；在此基础上，采用GBDT 算法对叠合面的黏结强度进行建模预测分析；并与支持向量回归（SVR）、K 近邻回归（KNN）、DT 和BPNN 这4 种经典模型的预测结果进行了综合对比.

1 试验样本

GBDT 作为端到端的机器学习模型，预测结果依赖于训练样本集规模与样本数据的可靠性等.石运良等［14］通过试验和数值模拟2 种方式综合获取了样本数据.考虑到数值模拟结果在一定程度上依赖于试验测试结果及数值模型的建立，本文所有样本数据均基于多因素多水平的正交试验.

设计制作尺寸为150 mm×150 mm×150 mm 的陶粒轻骨料混凝土与普通混凝土夹层叠合的双面直剪试块，如图1所示.试块浇筑时，先浇筑中间LWAC夹层部分，根据不同间隔时间再浇筑两侧NC 叠合层部分.图1 中F为叠合面法向作用力，q为试验作用均布荷载.LWAC 和NC 设计强度等级分别为LC30、C40.试验所用轻骨料为粉煤灰高强陶粒，筒压强度为8.4 MPa，堆积密度与表观密度分别为988、1 796 kg/m3；普通粗骨料为5～15 mm 连续级配的石灰岩碎石，堆积密度与表观密度分别为1 323、2 464 kg/m3；水泥采用海螺牌P·O 42.5 普通硅酸盐水泥；细骨料采用淡化后的中细海砂，粉煤灰采用镇海电厂Ⅱ级粉煤灰；采用自来水进行搅拌.LWAC 和NC 的配合比及28 d立方体抗压强度见表1.

表1 LWAC 和NC 的配合比及28 d 立方体抗压强度Table 1 Mix proportion and 28 d cubic compressive strength of LWAC and NC

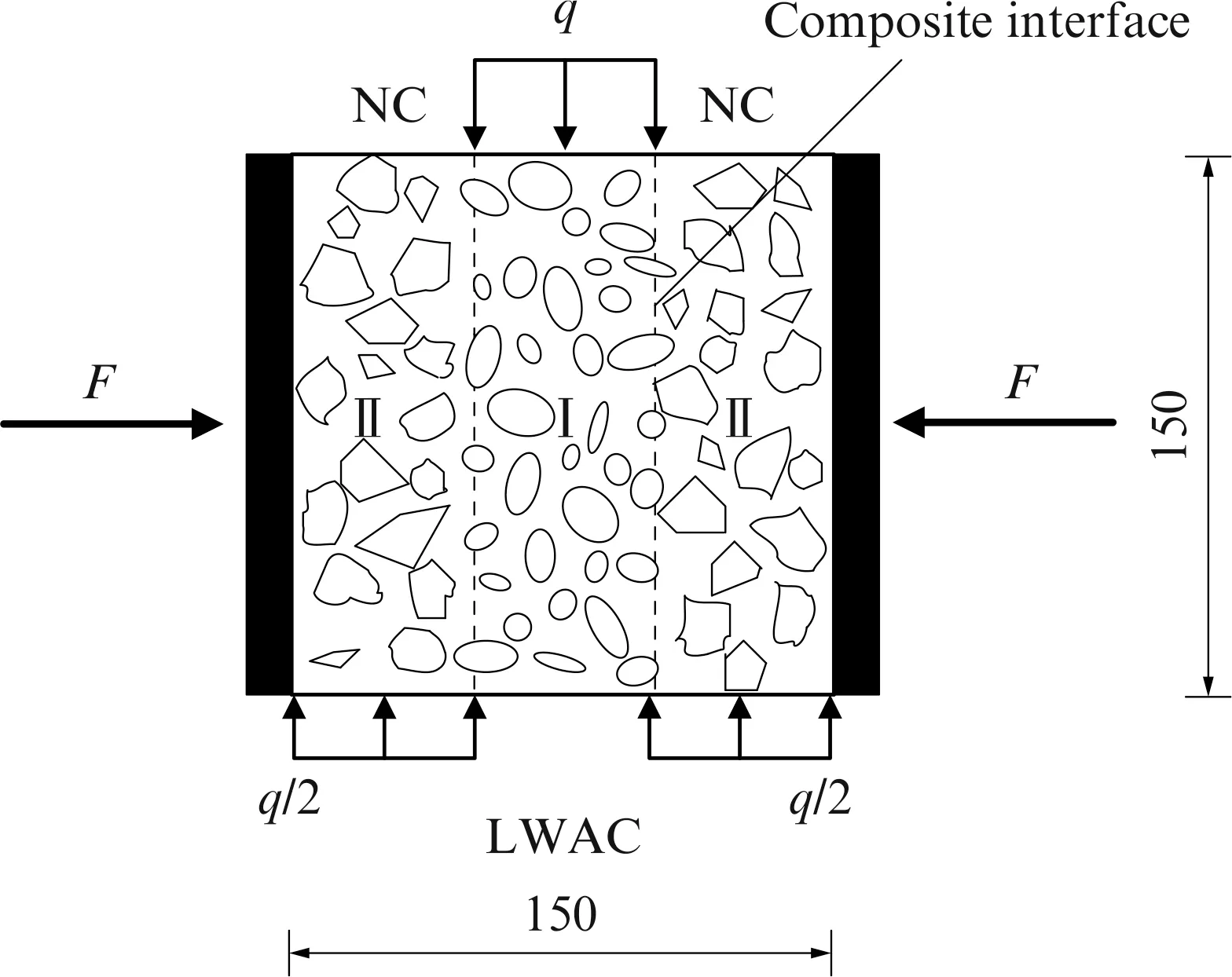
图1 双面叠合浇筑试块及试验加载示意图Fig.1 Diagram of sandwich composite blocks and loading scheme（size：mm）

考虑叠合面法向作用力F和浇筑间隔时间的变化，叠合面处理方式考虑人工刷毛、粉煤灰砂浆涂刷和露骨料剂处理这3 种方式.人工刷毛后叠合面平均粗糙程度控制为2～3 mm.叠合面法向作用力F取0、12.5、25.0、37.5、50.0、75.0、100.0 kN；浇筑间隔时间取10 h 及2、7、14、28 d.根据多因素多水平正交试验设计，选取具有代表性的参数组合进行36 组试验，具体见表2.每组试验包含3～5 个试块，其中包括1～2 块备用试块，结果取平均值.各组试块在实验室标准养护28 d 后按照图1 所示进行双面直剪试验.试验加载采用接触前位移控制、接触后力控制的方式，加载速率取0.5～0.8 MPa/s.采用千斤顶对试块分级施加法向荷载.

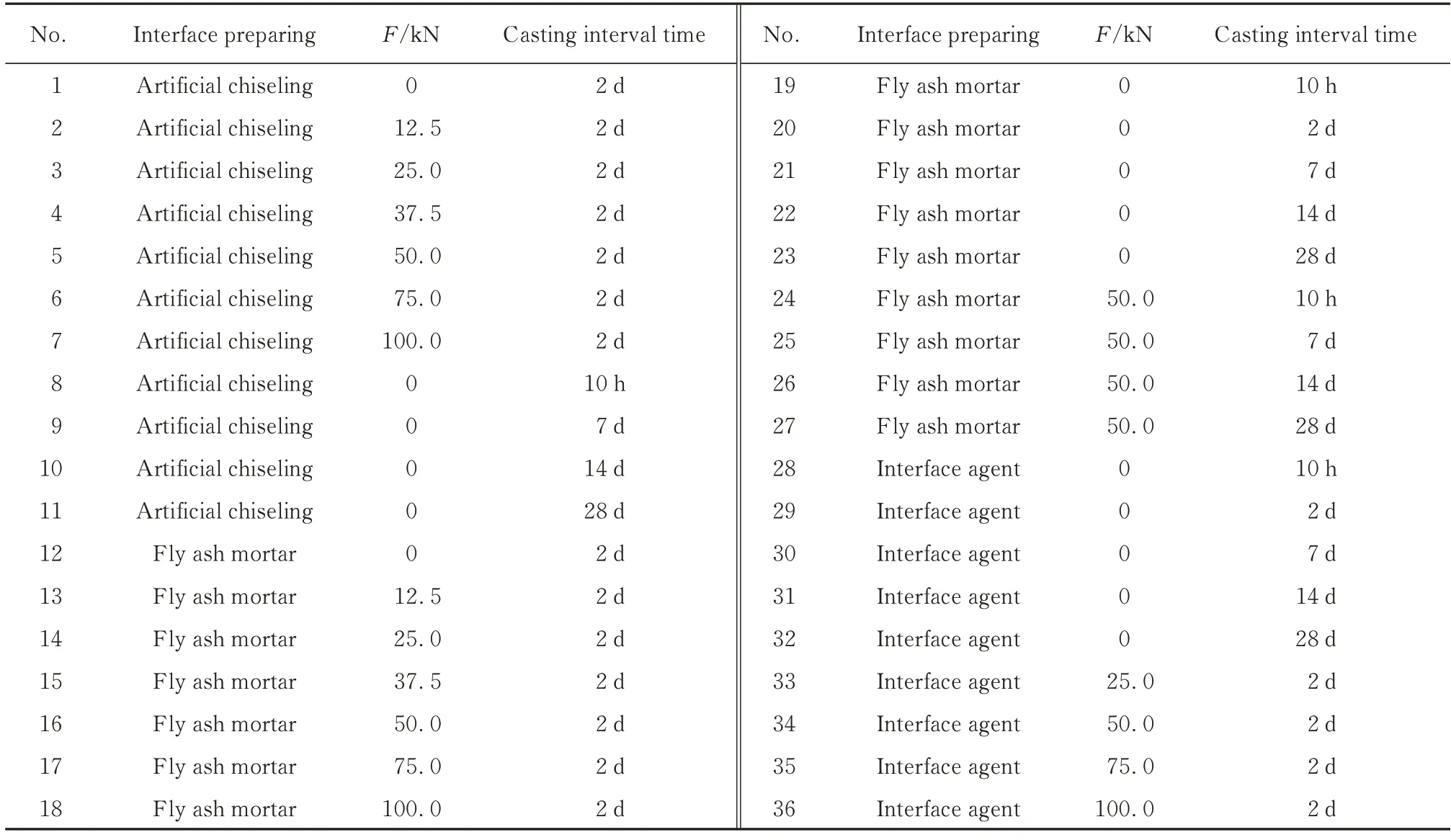
表2 试验样本分组Table 2 Groups of experimental samples

各试块黏结强度如图2 所示.由图2 可见，试块黏结强度随法向作用力的变化明显；试块黏结强度前期随浇筑间隔时间的变化明显，当浇筑间隔时间超过7 d 后，其变化相对平缓.

图2 各试块黏结强度Fig.2 Bonding strength of composite blocks

2 预测模型设计与建立

2.1 GBDT 模型

LWAC 与NC 叠合浇筑时，黏结强度与叠合面处理方式、法向作用力、浇筑间隔时间之间存在复杂的非线性关系，所考虑的3 个因素之间又相互影响.GBDT 作为一种以分类回归树（CART）为基本模型的集成学习算法，由决策树（decision tree）和梯度提升（gradient boosting）两部分组成.其基本学习器是回归树，作用是通过构造一个函数来拟合数据集D中的元素，使均方 误差最小.D=｛（x1，y1），（x2，y2），…，（xm，ym）｝为包含m个训练样本的数据集，每个样本由d个特征属性描述，即：xj=［xj1，xj2，…，xjd］；yj为对应样本的叠合面黏结强度.多个回归树模型按照一定的结合策略组成得到GBDT 集成学习器.

通过叠合面处理方式、法向作用力和浇筑间隔时间等条件属性，建立GBDT 集成学习拓扑模型，来预测陶粒轻骨料混凝土与普通混凝土叠合面的黏结强度，见图3.图3 中，Xi、Yi为相应的判据参数；Si为回归树模型中相应叶节点.

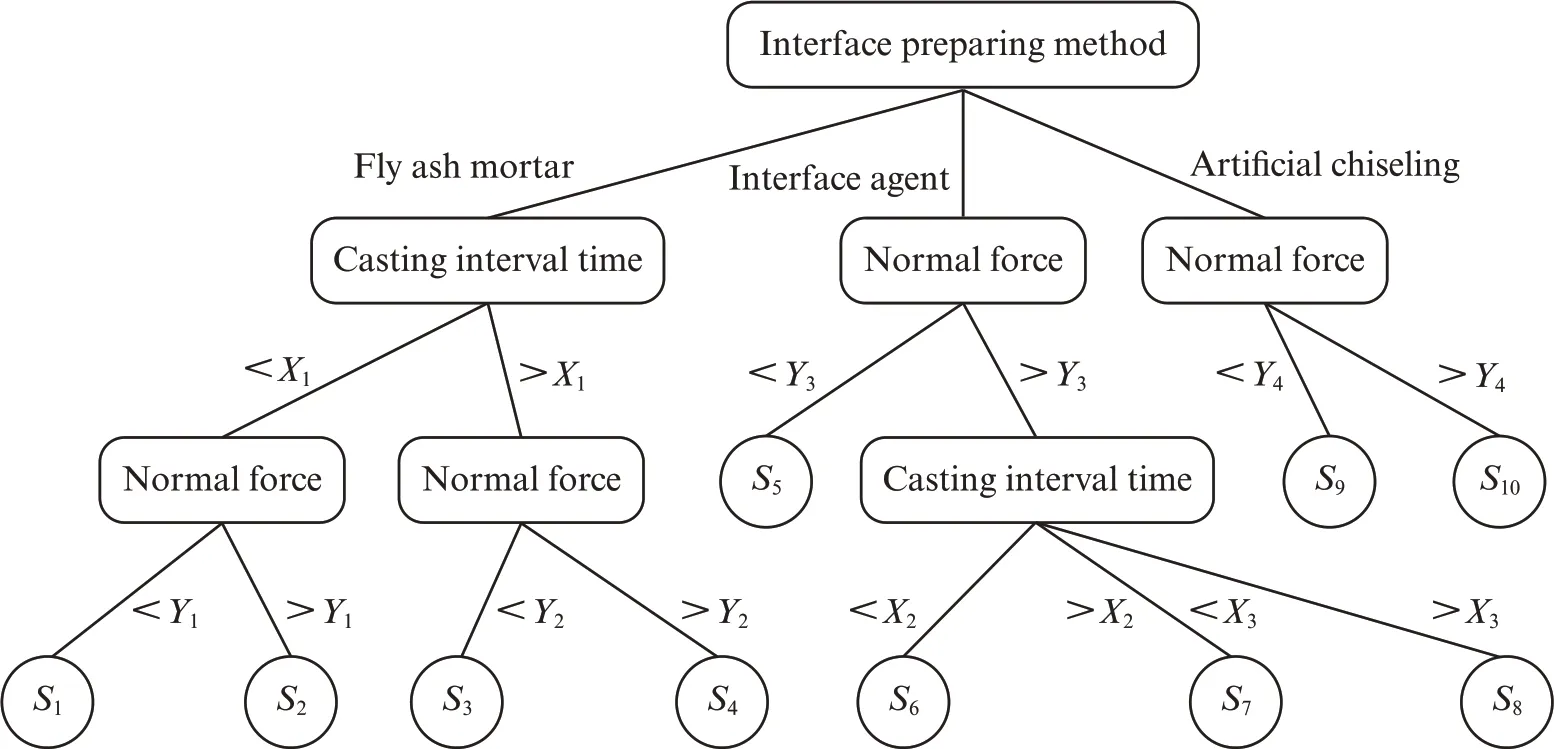
图3 GBDT 集成学习拓扑模型Fig.3 Topological model of GBDT ensemble learning algorithm

所建立的GBDT 模型基本算法流程如下：

（1）初始化基学习器f0（X）：

式中：X=［x1，x2，…，xm］；L（yj，α）为损失函数，用于计算真实值与预测值之间的误差；α为使损失函数最小化的常数.

（2）建立一系列CART 回归树，利用梯度提升技术拟合残差.在第k（k=1，2，…，K）次迭代中，对于每一个样本（xj，yj），GBDT 规定将损失值的负梯度作为残差估计值.本文选用平方损失函数，该函数的一阶导数连续且易于优化，被广泛应用于各种学习任务中.平方损失函数L表示如下：

故残差估计值Rjk为：

（3）确定了残差估计值后，利用CART 回归树进行拟合，得到第k棵树的叶节点区域为cjk（j=1，2，…，J），J为回归树叶节点个数.对于每个叶节点区域，可确定使对应平方损失函数最小化的最佳拟合值βjk：

（4）更新学习器fk（X）：

式中：η为学习率.

（5）迭代结束之后，形成GBDT 强学习器F(X)：

本文所建立的GBDT 模型将混凝土叠合面处理方式、法向作用力和浇筑间隔时间作为模型输入特征参数，模型输出特征参数为混凝土叠合面的黏结强度.根据分组试验共获取36 组样本数据.模型在训练和评估阶段，一般采用随机同分布和交叉验证理论划分训练集、验证集和测试集.本文在进行数据处理时，试验结果取每组试块试验结果的平均值yˉ，各组之间不是重复性试验.因此，按照5∶1 比例对总样本数据进行划分，即30 组样本数据构成模型训练样本集，剩余6 组样本数据作为模型测试样本集.按此比例分3 次划分训练样本集和测试样本集，对GBDT模型进行3 次训练和测试.

2.2 对比预测模型及参数调优结果

为了评价和检验GBDT 模型对叠合混凝土黏结强度的预测效果，本文同时建立了另外4 个经典机器学习模型：SVR、KNN、DT 和BPNN，在输入、输出特征参数和样本数据集划分不变的情况下，通过对各模型进行具体参数调优和训练，综合分析比较其预测结果.其中，SVR 通过寻找一个超曲面使期望风险最小，实现预测分析；KNN 算法利用距离其最近的K个“邻居投票”原理进行预测；DT 模型基于树的数据结构利用信息增益进行预测；BPNN 作为一种网状结构，通过BP 算法进行训练，学习某种规则，在给定输入值时得到最接近期望输出值的结果.

各模型预测结果采用拟合优度（R2）进行评价对比.同时，参考平均绝对误差（MAE）和均方根误差（RMSE）指标对各模型预测效果进行综合对比.其中，MAE 反映预测值和真实值之间的偏差，RMSE反映预测值和真实值之间差值的标准差，其具体计算方法如下：

式中：T为测试样本总数；pj为第j个测试样本的模型预测值.

本文GBDT 模型采用网格搜索法，在建模数据集上对模型的4 个超参数进行优化，其最优参数决策树个数为700，最大深度为3，叶节点最小样本数为1，学习率为0.05；SVR 模型采用线性核函数，惩罚参数C为10；KNN 模型超参数K设定为3，不考虑距离权重；对于DT 模型，采用均方差（MSE）作为结点分裂依据，叶节点最少样本数为1，不限制决策树最大深度；BPNN 模型采用双隐层，神经元个数分别为4 和4，采用Sigmoid 激活函数，优化算法采用拟牛顿法（L-BFGS）.

3 结果与分析

表3 给出了5 个模型经过3 次训练后，预测结果评价参数R2、MAE 和RMSE 的统计结果.其中，MAE 和RMSE 反映了模型对测试样本集的预测精度及模型的泛化能力.由表3 可见：GBDT 模型的拟合优度R2的平均值为0.976，优于其他4 个预测模型，其次是BPNN 模型，表明在所给样本集下GBDT 模型表现出更强的数据拟合能力；同时，GBDT 模型的MAE 和RMSE 均小于其他4 个预测模型.综合对比表明，GBDT 模型的整体预测性能优于其他模型，并具有较好的泛化能力.

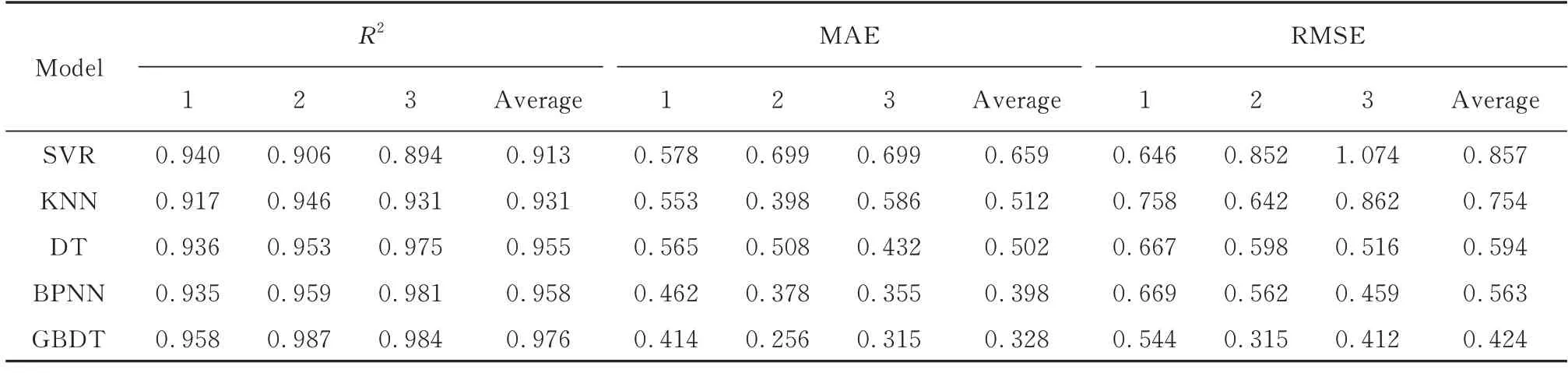
表3 模型预测结果评价参数Table 3 Evaluation parameters of prediction results from models

表4 给出了各模型对第3 组测试样本的预测结果及相对误差.由表4 可见：在6 个测试样本中，GBDT 模型在整体上可获得满意的预测结果，最小和最大相对误差分别为2.90%和8.64%，总体相对误差平均值为6.26%，明显小于其他4 个学习模型的预测结果.

表4 各模型对第3 组测试样本的预测结果及相对误差Table 4 Predicted results and relative errors of the third group of samples by different models

图4给出了GBDT 模型对3组测试样本预测结果的相对误差.由图4可见，除个别测试样本的相对误差较明显外，其余样本预测结果的相对误差均在±10%以内.不排除个别样本的试验结果可能存在较明显误差，从而对所建立模型的训练和预测造成一定程度的数据“噪声污染”，影响了模型的预测效果.

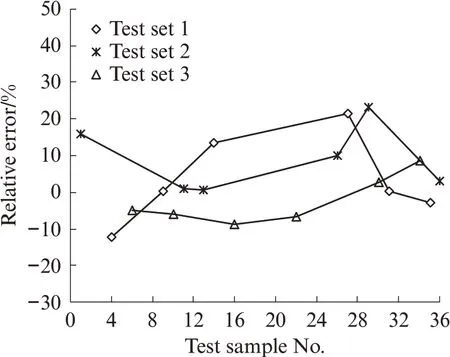
图4 GBDT 模型对3 组测试样本预测结果的相对误差Fig.4 Relative errors of three sets of test samples from GBDT model

4 结论

（1）与支持向量回归、K 近邻回归、决策树和BPNN 模型相比，GBDT 模型表现出良好的预测性能和泛化能力，在陶粒轻骨料混凝土与普通混凝土叠合面黏结强度预测分析中体现出良好的训练和预测优势.

（2）所建立的GBDT 模型的预测结果平均相对误差明显小于其他4 种模型，表明GBDT 模型在未知数据上表现出较好的预测性能，可获得整体满意的预测精度.

（3）本文现阶段试验样本数据仍较有限，仅考虑了叠合面处理方式、法向作用力和浇筑间隔时间这3 个输入特征参数.实际影响混凝土叠合面黏结性能的因素还包括混凝土材料性能、叠合面粗糙度和浇筑施工工艺等诸多因素.相关因素的筛选及其对混凝土叠合面黏结性能的影响和预测分析，以及机器学习模型的优化、泛化等仍有待进一步深入研究.