定向钢纤维增强水泥基复合材料断裂细观数值模拟

卿龙邦，杨子美，慕 儒，张金鑫，籍晓凯

（河北工业大学 土木与交通学院，天津 300401）

在水泥基体中加入适量的钢纤维可以有效抑制裂缝的扩展，改善水泥基复合材料的断裂性能［1-3］.研究表明，钢纤维的增强作用受其分布方向的影响［4-5］.在传统随机乱向钢纤维增强水泥基复合材料（SFRC）中，纤维呈随机乱向分布，部分纤维分布方向与拉应力方向并不一致，难以充分发挥其增强作用，将钢纤维按特定方向分布则可以明显提高其增强效率［6］.

采用磁场法可以实现钢纤维的定向分布.慕儒等［7-9］在盛有钢纤维增强水泥砂浆的试模外施加均匀电磁场，同时施加振动辅助，制备了定向钢纤维增强水泥基复合材料（ASFRC）并对其力学性能以及断裂性能进行了研究.Wijffels 等［10］利用钢纤维在磁场中磁化的特性，制备了钢纤维定向分布的水泥基复合材料，研究了定向钢纤维对复合材料弯曲性能的影响.王哲伟等［11］通过对钢纤维增强地质聚合物施加均匀电磁场，制备了定向钢纤维增强地质聚合物预制缺口梁.汪洋等［12］采用磁场诱导定向技术，制备了定向碳纤维增强水泥砂浆，研究了碳纤维的取向性对碳纤维增强水泥砂浆力学性能提升效果的影响.

细观数值模拟便于分析基体和钢纤维在断裂过程中任意时刻的受力状态，有利于深入研究钢纤维的增强机理.Wang等［13-14］通过分析钢纤维混凝土材料的应力-应变曲线，建立了钢纤维混凝土材料的本构关系，采用最大主应变破坏准则模拟了钢纤维混凝土在动态压缩荷载及爆破荷载下的破坏过程.Soetens等［15］假定纤维与基体无相对滑动，将纤维单元嵌入基体单元，建立了三维钢纤维混凝土有限元模型，模拟了端钩形钢纤维混凝土四点弯曲梁开裂的全过程.Fang等［16］建立了可预测SFRC 动态破坏的三维有限元模型，研究了高应变率下SFRC 的动态压缩性能.Yu等［17］在预计产生裂缝的截面处插入黏聚单元，将与裂纹张开速率相关的内聚定律作为黏聚单元的失效准则，模拟了端钩形钢纤维混凝土在不同落锤冲击速度下的断裂失效行为.

本文采用随机生成算法投放钢纤维，建立了SFRC 和ASFRC 三点弯曲梁细观有限元数值模型，计算了不同钢纤维掺量（体积分数）下SFRC 试件和ASFRC 试件加载断裂的全过程，结合断裂试验验证了数值模型的有效性，分析了开裂截面处的纤维应力，研究了定向钢纤维的细观增强机理.

1 数值模拟

1.1 纤维投放

在440 mm×100 mm×100 mm 区域内投放直径（Df）为0.5 mm，长度（Lf）为30 mm 的圆直型钢纤维，钢纤维总数量（N）通过以下方法确定［18］：

式中：V为投放区域的体积，mm3；Vf为钢纤维掺量，%.

在SFRC试件中，钢纤维呈随机分布.本文参考文献［18］，确定钢纤维掺量为0.8%，试件尺寸为440 mm×100 mm×100 mm，控制纤维投影与X轴的夹角（θ）分别为［0°，30°）、［30°，45°）、［45°，60°）、［60°，90°］，根据角度占比确定每种角度范围内的纤维数量Ni（i=1，2，3，4），分次投放钢纤维，直到投放的纤维总数量为N，建立不同角度范围内的随机乱向钢纤维细观数值模型，如图1所示.

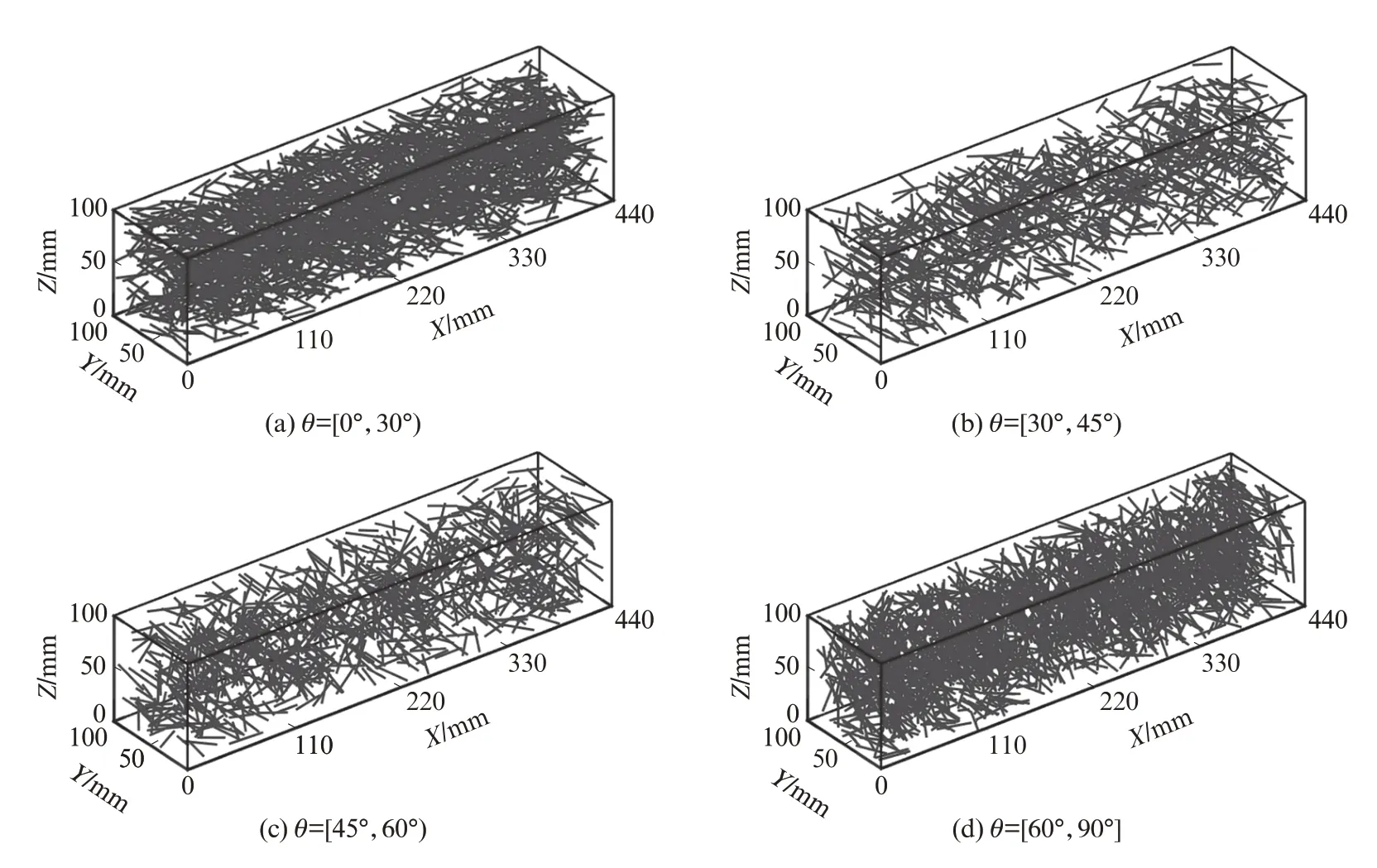
图1 不同角度范围内的随机乱向钢纤维细观数值模型Fig.1 Meso-numerical model of random steel fibers in different angle ranges

在ASFRC 试件中，钢纤维分布方向与主拉应力方向一致，基于随机乱向钢纤维的投放算法，确定钢纤维掺量为0.8%，试件尺寸为440 mm×100 mm×100 mm，控制纤维投影与X轴夹角为0°，建立定向钢纤维细观数值模型，如图2 所示.

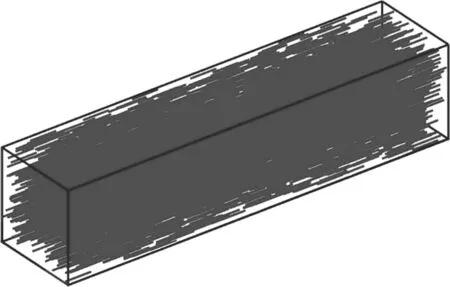
图2 定向钢纤维细观数值模型Fig.2 Meso-numerical model of aligned steel fibers

1.2 建立模型

1.2.1 基体本构关系

基体选用三维八节点实体单元建模，钢纤维选用三维二节点桁架单元建模.采用黏聚裂纹模型［19］计算基体的开裂.在三点弯曲梁有限元模型跨中处插入零厚度的黏聚单元，将牵引分离定律作为黏聚单元的失效准则［20-22］，以黏聚单元的失效来模拟试件裂缝的产生和扩展.三点弯曲梁模型跨中处钢纤维的分布如图3所示（以钢纤维掺量0.8%的试件为例）.

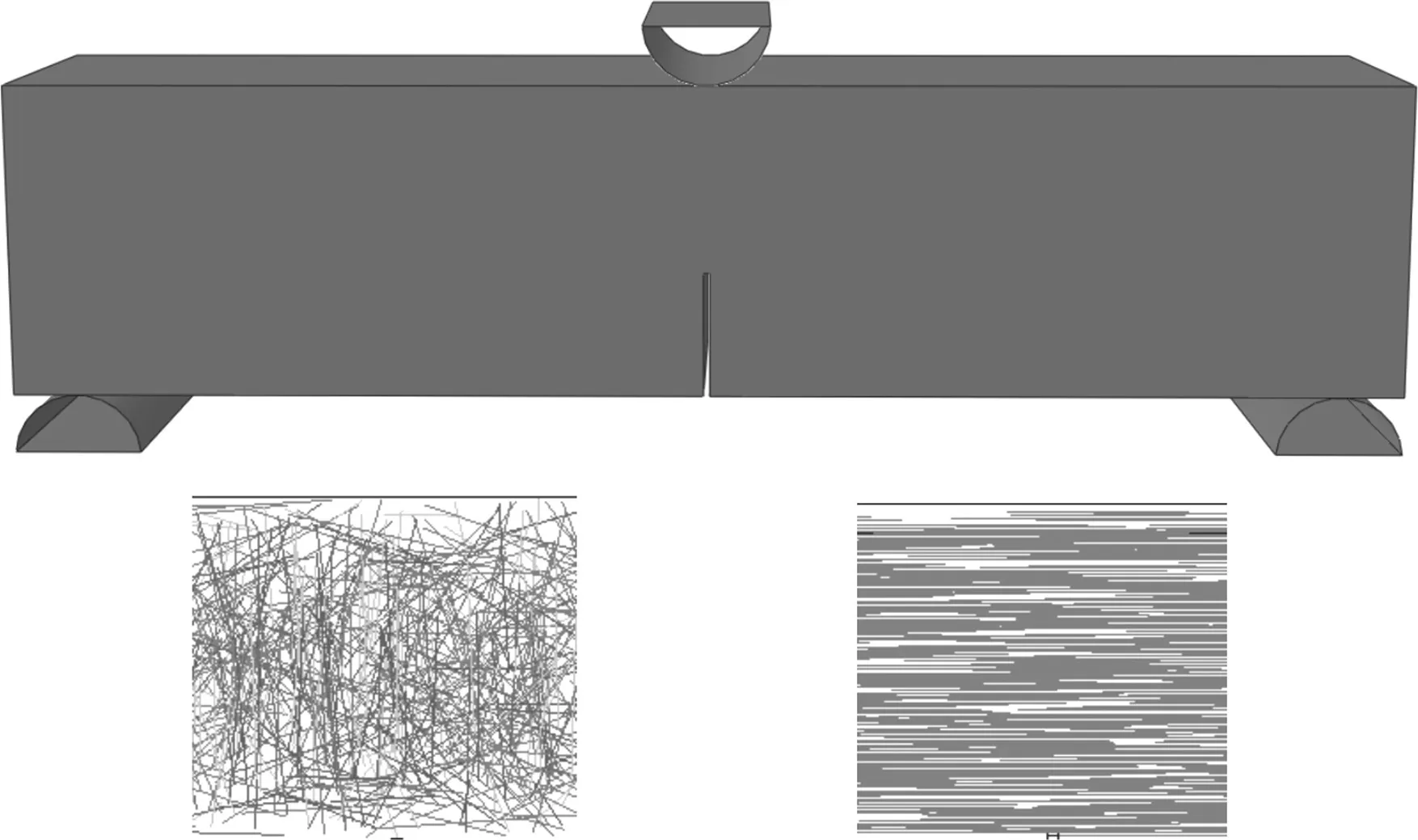
图3 三点弯曲梁模型跨中处钢纤维的分布Fig.3 Distribution of steel fibers in the middle of the three point bending beam model

1.2.2 钢纤维与水泥界面的本构关系

在建立钢纤维增强水泥基复合材料细观有限元数值模型时，通常认为钢纤维和基体完全黏结，无相对滑动，因此将单根钢纤维与水泥砂浆基体拉拔试验所得拉拔力-位移曲线等效为钢纤维的拉伸应力-应变关系［23-25］，以此来模拟纤维与砂浆基体的黏结滑移作用.

拉拔试验使用P·O 42.5 普通硅酸盐水泥、细度模数为2.6 的天然河砂和自来水来制作水泥砂浆基体，钢纤维为弹性模量210 GPa 的圆直型钢纤维.钢纤维埋深（Hf）为20 mm，埋入角度为0°、30°、45°、60°，每种角度制备10 个试件，试件尺寸为100 mm×100 mm×100 mm.拉拔试验在SUNS20kN 型万能试验机上进行，加载速度为0.4 mm/min，当钢纤维被完全拔出或被拔断时结束试验.图4 为倾斜纤维加载示意图.

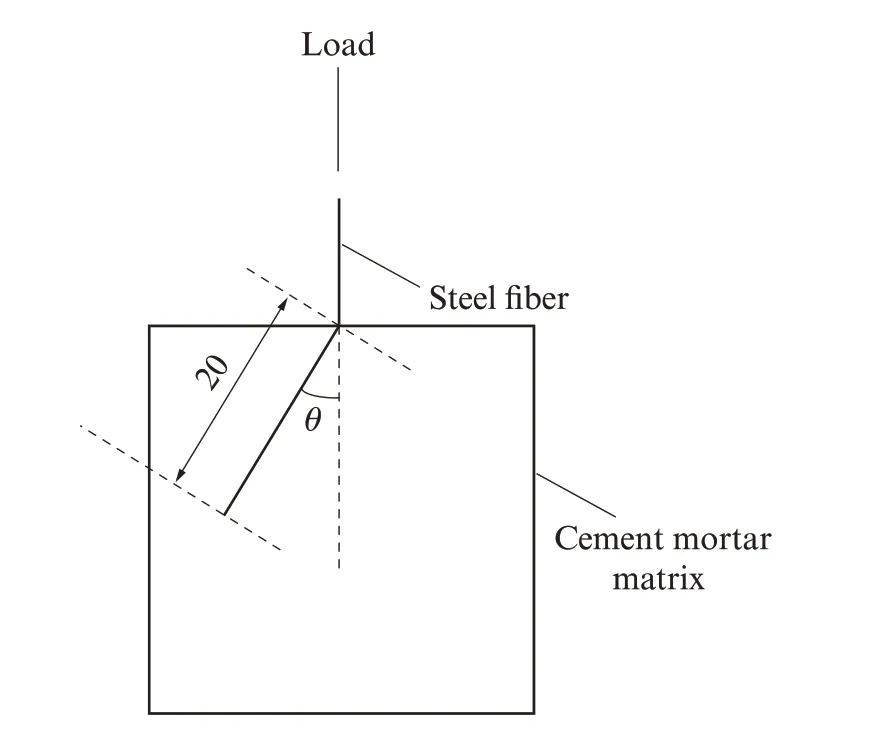
图4 倾斜纤维加载示意图Fig.4 Schematic diagram of inclined steel fiber loading（size：mm）

钢纤维的拉拔力-位移曲线如图5 所示.每种埋入角度取3 组离散性较小的数据作为试验结果.采用理论计算公式对试验拉拔力-位移曲线进行计算［26-27］，结果如图5 所示.由图5 可见：

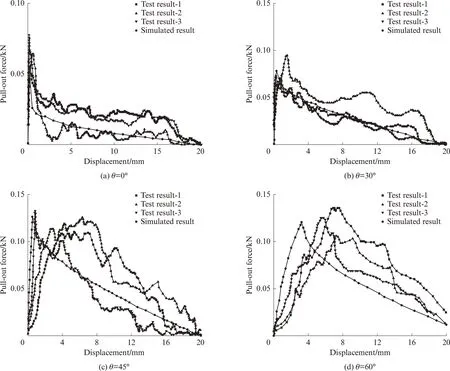
图5 钢纤维的拉拔力-位移曲线Fig.5 Curves of pull-out force-displacement of steel fiber

（1）峰值荷载的理论计算结果与试验结果相差不大，位移存在一定误差.这是钢纤维倾斜角度增大导致的测量误差，总体上理论计算结果与试验结果吻合.

（2）当埋入角度小于45°时，钢纤维拉拔力-位移曲线的峰值荷载随着埋入角度的增加逐渐增大且向右偏移；当埋入角度大于45°时，峰值荷载有减小的趋势.这是因为当纤维倾斜角度过大时，纤维埋入端处的基体应力集中程度加重，水泥砂浆破坏速度加快，使钢纤维被拔出所需要的拉拔力变小.

为计算简便，在开展有限元模拟分析时，将理论计算的拉拔力-位移曲线等效为钢纤维的拉伸应力-应变关系，如图6 所示.当纤维倾斜角度为0°时，参考文献［18］进行等效计算；当倾斜角度不为0°时，引入几何校正系数（θ(Sf)）、等效应力（σf）和等效应变（εf），按式（2）～（4）进行计算.

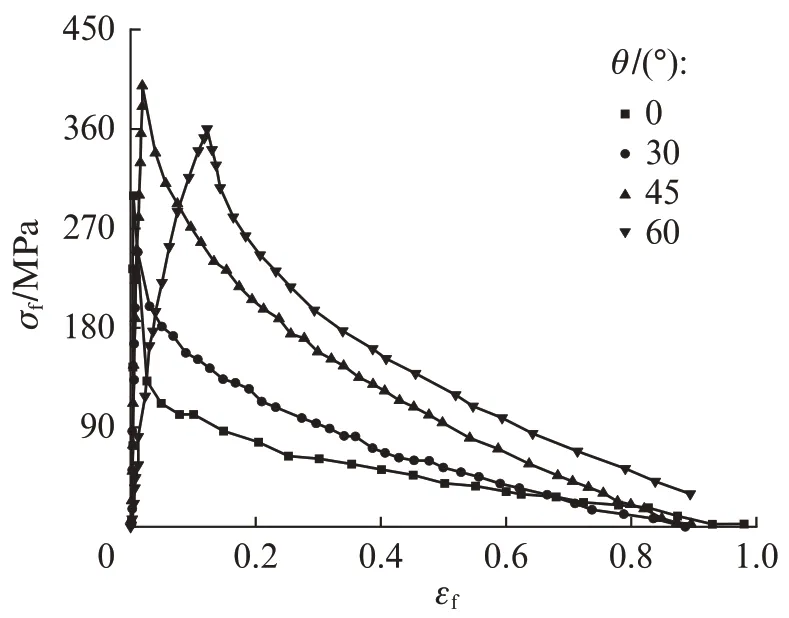
图6 基于拉拔力-位移曲线确定的钢纤维等效应力-应变关系曲线Fig.6 Determination of steel fiber stress-strain curves base on pull-out force-displacement curves

式中：Ff为钢纤维拉拔荷载，kN；Sf为钢纤维滑移位移，mm；θ0为钢纤维与拉拔力之间的初始夹角，（°）.

根据纤维投影与X轴的夹角范围，分别指定相应角度的等效应力-应变关系.基于扩展有限元法，采用位移加载的方式模拟荷载作用下SFRC 和ASFRC 三点弯曲梁断裂破坏的全过程.

2 断裂试验

采用P·O 42.5 普通硅酸盐水泥、细度模数为2.6的天然河砂、钢纤维、自来水和聚羧酸型高效减水剂来制作钢纤维增强水泥砂浆.调试后确定基体水灰比（质量比）为0.36，设计纤维掺量为0.8%、1.2%、2.0%，具体的材料配合比见表1.钢纤维的特征参数见表2.其中：E为弹性模量，ft为抗拉强度.

表1 砂浆基体的配合比Table 1 Mix proportions of mortar matrix

表2 钢纤维的特征参数Table 2 Characteristic parameters of steel fibers

每种钢纤维掺量下均制备SFRC 试件和ASFRC试件，试件尺寸为440 mm×100 mm×100 mm，跨高比为4，跨中设置宽2 mm 的预制裂缝，缝高比为0.4，标准养护28 d.制备SFRC 试件时采用常规方式振捣，制备ASFRC 试件时需将盛有钢纤维增强水泥砂浆的试模置于振动台上的通电线圈内进行振捣，如图7 所示.

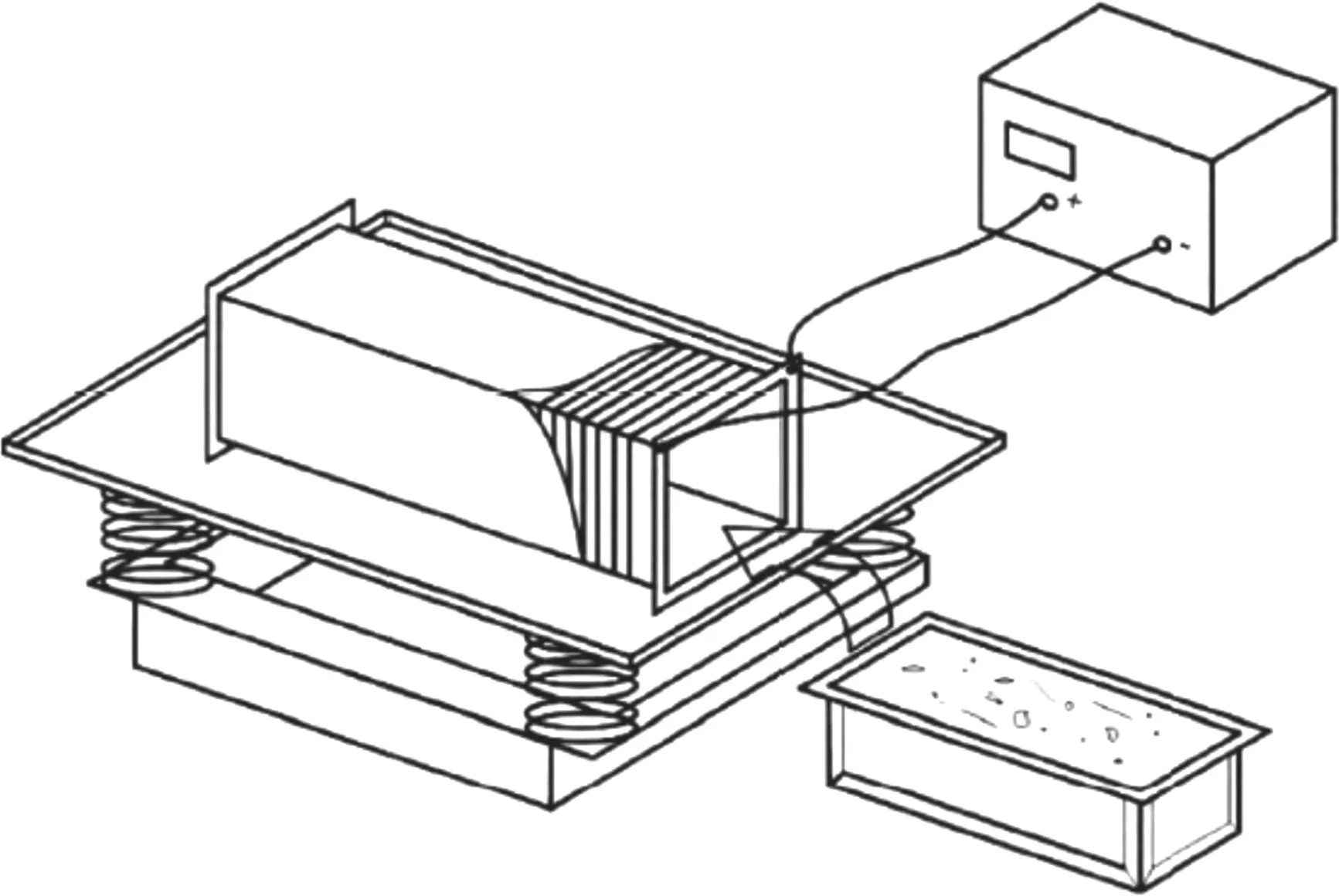
图7 ASFRC 试件的制备装置Fig.7 Preparation device of ASFRC specimen［8］

断裂试验在伺服万能试验机上进行，采用位移加载方式，加载速率为0.15 mm/min.选用量程为20 kN 的外接荷载传感器测量荷载（P），在试件裂缝跨中底部设置YYJ-10/10 型夹式引伸计，用于测量裂缝张开位移（CMOD）.试验加载示意图如图8 所示.水泥砂浆基体的材料力学参数如表3 所示.其中：μ为泊松比，GF为断裂能.

图8 断裂试验加载示意图Fig.8 Loading schematic diagram of fracture test（size：mm）

表3 水泥砂浆基体的材料力学参数Table 3 Material mechanical parameters of cement mortar matrix

3 结果及分析

3.1 P-CMOD 曲线及峰值荷载

SFRC 试件和ASFRC 试件的荷载-裂缝张开口位移（P-CMOD）曲线如图9所示.由图9可见：

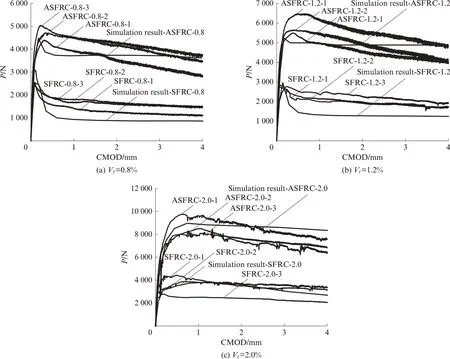
图9 SFRC 试件和ASFRC 试件的荷载-裂缝张开口位移曲线Fig.9 P-CMOD curves of SFRC and ASFRC specimens

（1）当钢纤维掺量为0.8% 时，SFRC 试件的P-CMOD 曲线有明显的陡降，随着钢纤维掺量的增加，陡降程度有所缓解，而ASFRC试件的P-CMOD曲线在达到峰值荷载后均下降缓慢.这是因为钢纤维定向后，其分布方向与试件所受主拉应力方向一致，桥接裂缝的钢纤维得到了充分利用，阻裂增韧效率提高.

（2）当钢纤维掺量为0.8%和1.2%时，SFRC 试件模拟曲线的下降段略低于试验曲线，但曲线趋势大致相同，当钢纤维掺量为2.0%时，曲线吻合较好；ASFRC 试件的模拟曲线与试验曲线均吻合较好.因此，模拟结果可以较好地反映2种试件断裂的全过程，表明建立的细观有限元数值模型具有一定的有效性.

试验与模拟所得SFRC 试件和ASFRC 试件的峰值荷载如表4 所示.每组3 块试件，取平均值作为该组的试验峰值荷载.由表4 可见：SFRC 试件和ASFRC 试件的试验峰值荷载均随着钢纤维掺量的增加而增大，且ASFRC 试件的峰值荷载的增幅大于SFRC 试件；当钢纤维掺量为0.8%、1.2%、2.0%时，ASFRC 试件的峰值荷载较SFRC 试件约提高了75%、111%、141%，表明钢纤维定向可以有效改善水泥基复合材料的断裂性能，提高钢纤维的利用率，充分发挥增强作用；3 种钢纤维掺量下，SFRC 试件峰值荷载模拟值与试验值的误差分别为6.30%、6.45%、4.07%，ASFRC 试件的误差分别为4.87%、9.01%、0.79%；2种试件的误差均在10%以内，误差较小.

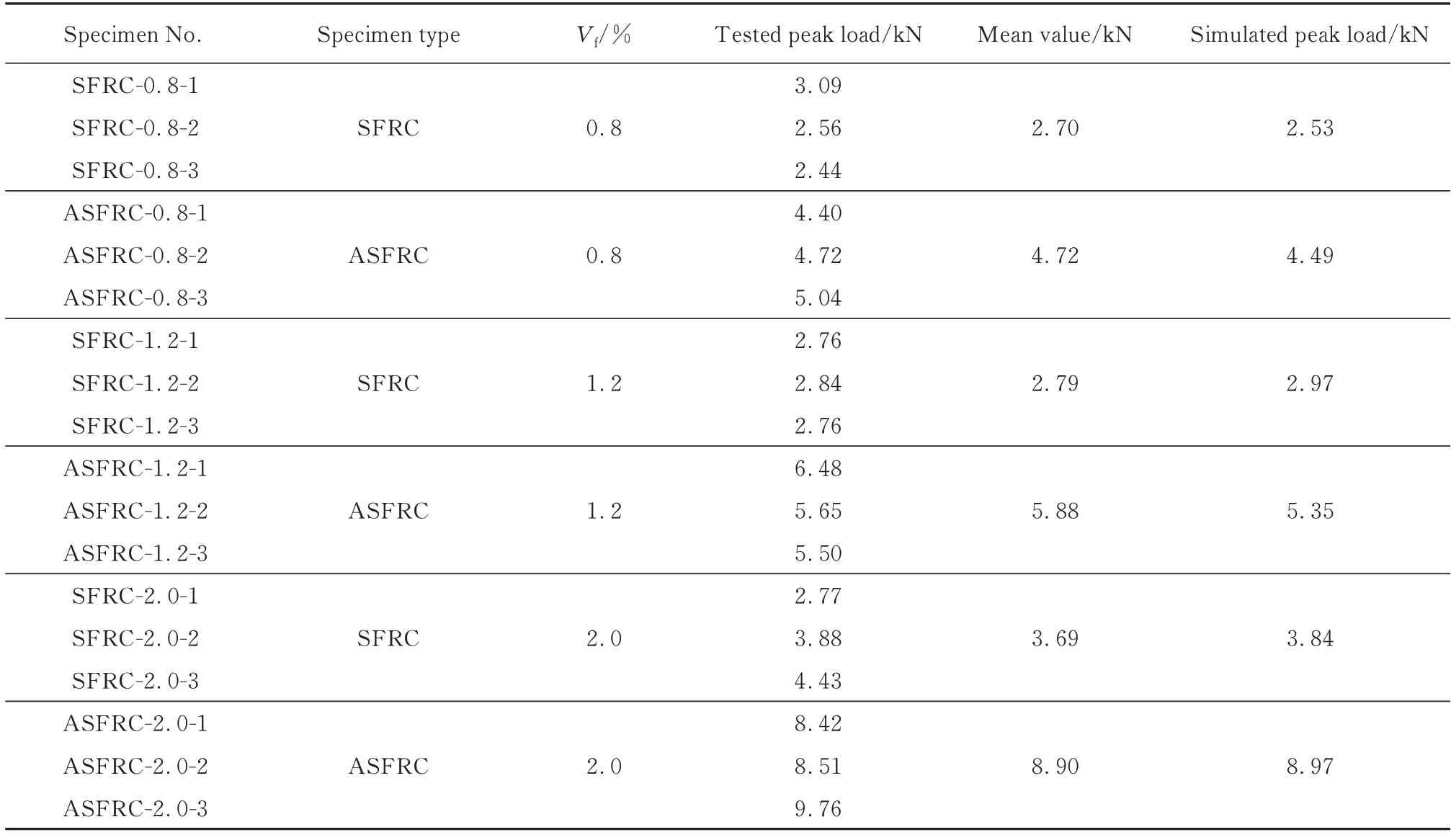
表4 试验与模拟所得SFRC 试件和ASFRC 试件的峰值荷载Table 4 Tested and simulated peak loads of SFRC and ASFRC specimens

3.2 跨中开裂截面处纤维的应力分析

图10 为试件开裂破坏图及跨中开裂截面处的钢纤维分布.由图10 可见，SFRC 试件中的钢纤维呈乱向分布，难以充分发挥桥接裂缝的作用，而ASFRC试件中的钢纤维全部与开裂面垂直.

图10 试件开裂破坏图及跨中开裂截面处的钢纤维分布Fig.10 Cracking failure diagram of the specimen and distribution of steel fibers at the cracked section in the middle

不同加载时刻ASFRC 试件主拉应力方向（σx）的应力云图如图11 所示（以钢纤维掺量1.2%的试件为例）.由图11 可见：在加载初期，裂缝尚未产生，基体和钢纤维共同发挥承载作用（图11（a））；当P=3.52 kN 时，基体已产生裂缝（图11（b））；随着荷载的继续增加，裂缝向上扩展，基体逐渐退出工作，钢纤维与基体之间的黏结滑移发挥主要承载作用，消耗大部分能量，增强基体开裂后的延性（图11（c））；裂缝处钢纤维的应力减小，表明钢纤维开始滑动拔出，继续加载，试件逐渐丧失承载能力，沿着裂缝破坏（图11（d）、（e））.

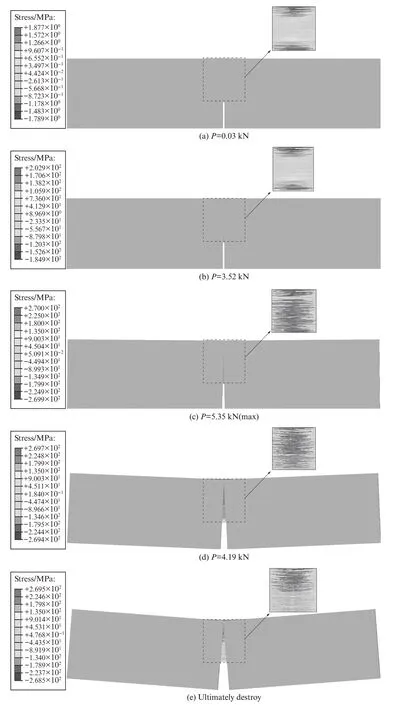
图11 不同加载时刻ASFRC 试件的主拉应力方向应力云图Fig.11 σx stress cloud diagram of ASFRC specimen at different loading moments

图12 为试件跨中开裂截面处的纤维应力分布图（以钢纤维掺量1.2%的试件为例）.以ASFRC 试件为例进行分析：在加载初期，纤维合力（F）较小，开裂截面处上部钢纤维受压，下部钢纤维受拉（见图12（b））；随着荷载的增加，受拉区域扩大，受拉钢纤维的数量增加，钢纤维合力逐渐增大（见图12（d）、（f））；当钢纤维合力增至最大值时，只有试件顶部少量钢纤维受压（见图12（h））；继续加载，钢纤维合力减小，试件逐渐丧失承载能力，沿着裂缝破坏；ASFRC 试件跨中开裂截面上的钢纤维数量明显大于SFRC试件，SFRC试件和ASFRC试件的钢纤维合力最大值分别为7.082 kN 和17.283 kN（见图12（g）、（h）），ASFRC 试件的钢纤维合力最大值较SFRC 试件约提高了144%，表明钢纤维定向后的利用率有大幅度提升.

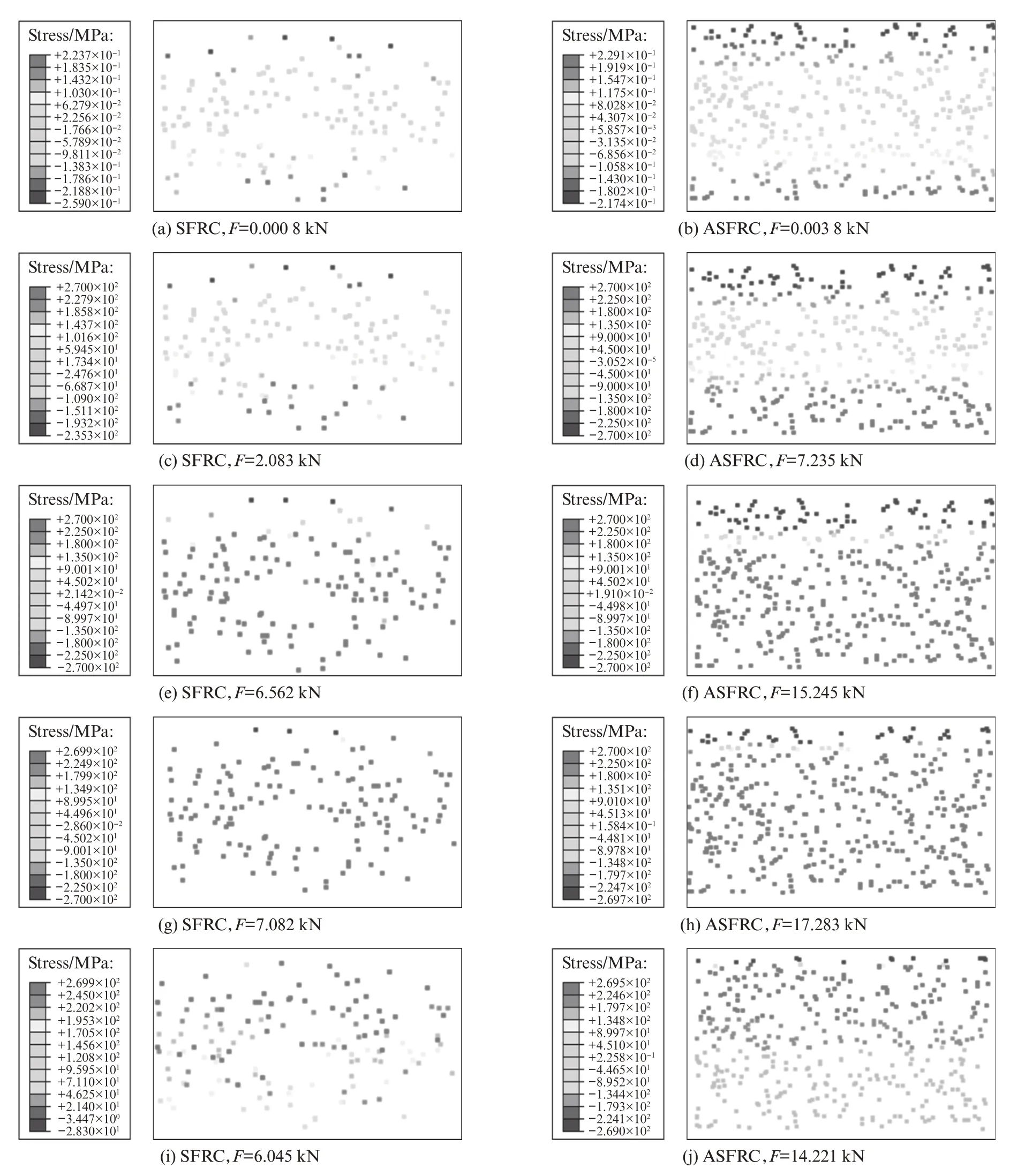
图12 试件跨中开裂截面处纤维的应力分布图Fig.12 Fiber stress distribution diagram on cracked surface in mid-span of specimens

图13 为试件跨中开裂截面处的钢纤维合力-荷载（F-P）曲线图.由图13 可见：

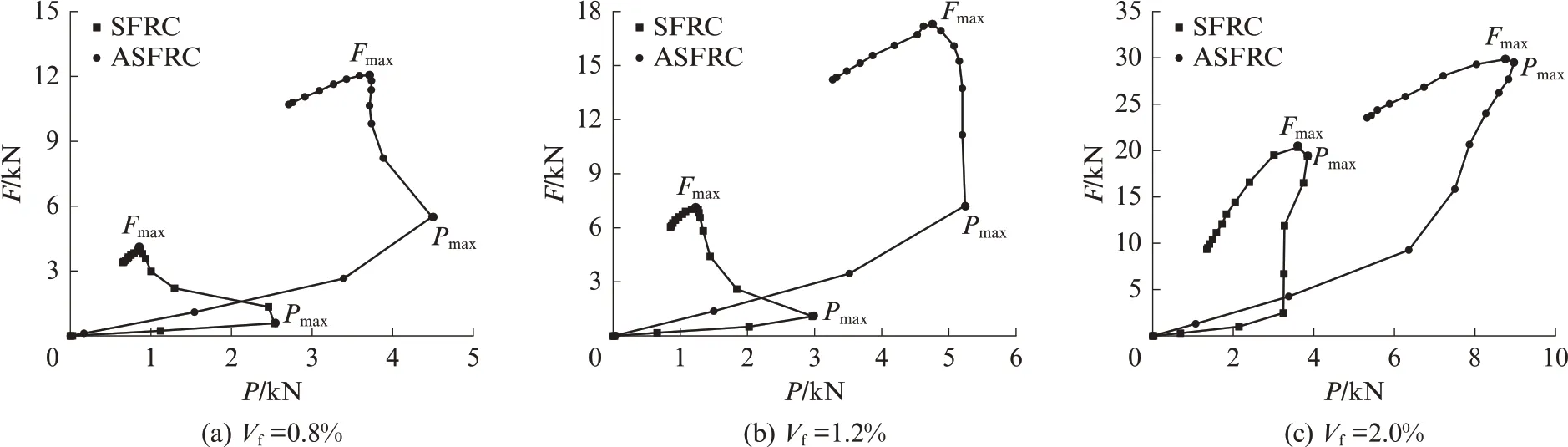
图13 试件跨中开裂截面处的纤维合力-荷载曲线图Fig.13 F-P curves of fibers on cracked surface in mid-span of specimens

（1）当钢纤维掺量为0.8%、1.2%、2.0% 时，SFRC 试件的钢纤维合力最大值分别为3.985、7.082、8.970 kN，ASFRC 试件的钢纤维合力最大值分别为12.047、17.283、20.361 kN，ASFRC 试件钢纤维合力的最大值较SFRC 试件分别增大了约202%、144%、127%，且ASFRC 试件的增幅随着钢纤维掺量的增加而减小.

（2）2 种试件的钢纤维合力均先增大后减小，且当钢纤维掺量相同时，在整个加载过程中ASFRC 试件的钢纤维合力始终大于SFRC 试件.在加载初期，钢纤维合力近似为线性增长，钢纤维处于弹性阶段，此时的伸长量为自身弹性变形；随着荷载的增加，裂缝开始向上扩展，钢纤维合力呈非线性增长，当达到峰值荷载时，开裂面上钢纤维的端部开始与基体脱黏，由钢纤维侧面与基体的黏结力承载主要荷载，基体开裂后的延性增强；荷载减小，钢纤维合力继续增大，当钢纤维合力增至最大值时，钢纤维与基体完全脱黏；钢纤维合力减小表明纤维被拔出，此时由钢纤维未拔出部分与基体之间的摩擦力共同抵抗荷载作用，继续加载，试件逐渐丧失承载能力，沿裂缝破坏.当钢纤维掺量为2.0%时，F-P曲线上的Pmax点和Fmax点较钢纤维掺量为0.8%和1.2%时更接近，这是由于随着钢纤维纤维掺量的增加，峰值荷载逐渐增大，同时钢纤维掺量的增加使钢纤维间距减小，钢纤维与基体之间的黏结作用减小，更易滑动被拔出，钢纤维合力增大的幅度减小，由此Pmax点和Fmax点较为接近.

4 结论

（1）钢纤维拉拔力的峰值随着钢纤维倾角的增加呈现先增大后减小的趋势.

（2）随机乱向、定向钢纤维增强水泥基复合材料（SFRC、ASFRC）试件的峰值荷载均随着钢纤维掺量的增加而增大，相同钢纤维掺量下ASFRC 试件的峰值荷载明显大于SFRC 试件.当钢纤维掺量为0.8%、1.2%、2.0%时，ASFRC 试件的峰值荷载较SFRC 试件分别提高了75%、111%、141%，表明钢纤维定向可以有效改善钢纤维增强水泥基复合材料的断裂性能.

（3）SFRC 和ASFRC 三点弯曲梁断裂全过程荷载-裂缝张开口位移全曲线的计算值与试验值符合较好，峰值荷载误差在10%以内，验证了有限元模型的有效性.

（4）当钢纤维掺量相同时，ASFRC 试件跨中开裂面上的钢纤维数量大于SFRC 试件；当钢纤维掺量为0.8%、1.2%、2.0%时，ASFRC 试件纤维合力的最大值较SFRC 分别提高了202%、144%、127%.表明钢纤维定向后可以显著提高钢纤维的利用率，延缓裂缝的扩展.