三角形内接三角形周长最小值及其应用

万福昌 吴 静

江苏省苏州市相城区陆慕高级中学 (215131)

本文探求三角形内接三角形周长的最小值，并利用其最小值得出两个有趣的定理.

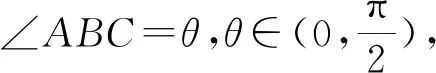
图1

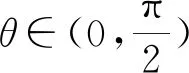
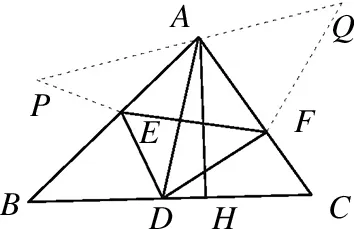
图2

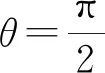
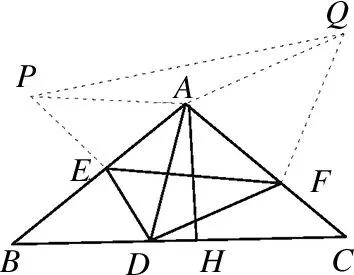
图3

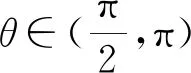
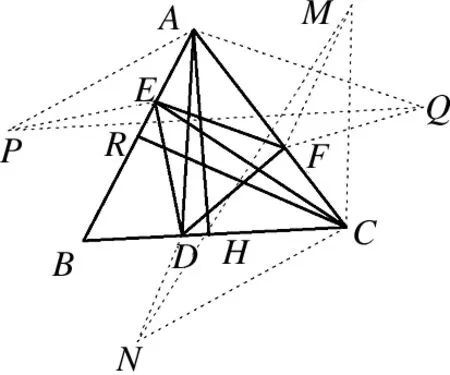
图4

定理2 如图4，在△DEF的三个顶点分别在三角形△ABC的三边上，AH是△ABC的BC边上的高，分别作D关于AB,AC的对称点P,Q分别作C关于CD,CB的对称点M,N，则PQ=MN.

证明：PQ,MN均为则△DEF周长等于PE+EF+QF的最小值，所以PQ=MN.

定理3 已知三角形△ABC的三边上的高分别为AH，BK,CR,则AHsin∠BAC=BKsin∠ABC=CRsin∠ACB.

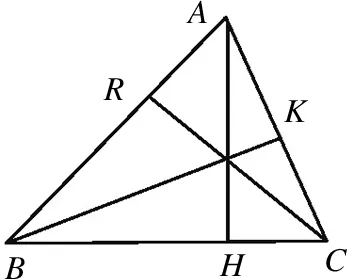
图5

证明：如图5，由命题1知PQmin=2AHsinθ，同理MNmin=2CRsin∠ACB，由命题2知PQ=MN，∴PQmin=MNmin，

∴AHsin∠BAC=CRsin∠ACB，同理BKsin∠ABC=CRsin∠ACB，故AHsin∠BAC=BKsin∠ABC=CRsin∠ACB.

定理3可称为垂弦定理.还可以通过如下方法证明.

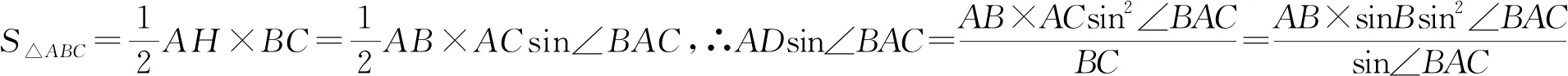
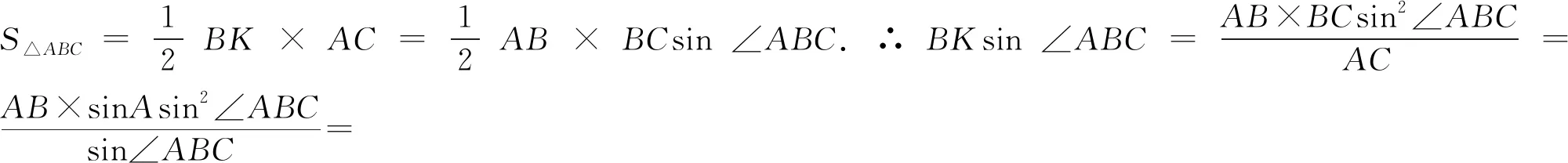
∴AHsin∠BAC=BKsin∠ABC.同理BKsin∠ABC=CRsin∠ACB.故AHsin∠BAC=BKsin∠ABC=CRsin∠ACB.