裂纹闭合临界状态磁特性表征模型
2023-03-11邢海燕朱孔阳段成凯刘伟男
邢海燕 朱孔阳 张 钋 刘 传 段成凯 刘伟男 刘 超
东北石油大学机械科学与工程学院,大庆,163318
0 引言
裂纹闭合是影响裂纹扩展的重要因素[1],裂纹闭合的存在会减小裂纹扩展的应力强度因子幅值,改变裂纹扩展速率,影响裂纹演化进程[2]。与高周疲劳裂纹扩展相比,裂纹闭合对低周疲劳扩展的影响更显著[3],而塑性诱导裂纹闭合即塑性致闭,是导致低周疲劳裂纹闭合的主要原因[4],因此塑性致闭的研究对低周裂纹扩展至关重要。传统的闭合状态测定方法,一是直接通过观测裂纹面之间距离来测定,二是间接通过柔度曲线或裂纹扩展速率来测定[5],而这些方法在实际工程中难以实施,因此急需能够对裂纹闭合进行简便高效测定的新方法。
裂纹闭合现象最早由ELBER[6]在20世纪70年代发现,随后,国内外学者在此基础上进行了大量裂纹闭合研究。从塑性致闭的机理出发,NEWMAN等[7]验证了塑性致闭会使裂尖应力-应变场分布改变,导致应力强度因子幅值减小,裂纹扩展速率下降;AUTUNES等[8]研究了裂尖张开位移、塑性应变范围等参数与裂纹闭合现象的联系,发现裂纹发生闭合会直接改变裂尖参数,从而影响裂纹扩展速率。还有一些研究发现,裂尖应力-应变场等参数反过来会影响裂纹闭合现象。杨平等[9]对AH32钢板进行低周疲劳实验和仿真,发现在裂纹扩展过程中裂尖累积塑性变形的增加会导致塑性尾迹中残余压应力减小,使闭合效应减弱;胡殿印等[10]研究了反向塑性区对闭合效应的影响,建立了基于裂尖张开位移的裂纹闭合模型。在裂纹扩展速率及寿命预测方面,马硕等[11]考虑闭合效应的影响,提出了寿命评估模型,并验证了模型的准确性和可行性。随着对裂纹闭合现象研究的深入,对裂纹闭合的测定成为研究的重中之重。对于闭合状态的测定,目前国内外常用的方法是基于Elber柔度曲线的间接法,主要包括裂纹张开位移法[12]、数字图像相关技术[13]等,但这些方法在实际工程中实现起来比较复杂,无法对裂纹闭合进行便捷高效地测定和表征。
磁记忆检测技术由DOUBOV[14]提出,是以力磁效应为机理,集力学、磁性物理学、金属材料学于一体的新兴无损检测技术。与传统无损检测技术相比,力磁效应[15]使得磁记忆技术能够通过磁学物理量与力学物理量之间的内在联系表征铁磁性材料裂尖应力集中区状态、反映早期的塑性应变,因而在表征塑性致闭方面有独特的优势。
本文以Q235B钢为实验材料,获取裂纹张开和闭合演化过程不同路径上的磁特性参数,研究裂纹塑性区对磁场分布的影响,结合裂纹张开位移法和柔度微分法分别得到柔度及柔度微分曲线,对比分析裂纹闭合过程中柔度微分曲线与合成磁特性参数ΔHp曲线,发现两者变化规律有较强的相关性,进而通过磁特性参数的临界特征对裂纹闭合状态进行判断,建立基于磁特性参数的裂纹闭合表征模型。
1 实验
1.1 实验材料及制备
实验材料采用工程中广泛应用的Q235B钢,其基本力学参数如表1所示,根据GB/T 21143—2014制备三点弯曲标准试样,尺寸135 mm×30 mm×15 mm,预制5 mm等幅疲劳裂纹,待测路径分别通过疲劳裂纹的裂尖和裂尾,便于准确地控制检测位置,如图1所示,两条检测路径长度均为80 mm。

表1 Q235B钢力学性能

图1 试件的几何尺寸及表面待测路径Fig.1 Specimen size and testing lines
1.2 实验设备及方法
实验使用MTS-880低周疲劳实验机(图2a),预制5 mm疲劳裂纹时,三点弯曲实验压载荷基值为8.8 kN,幅值为7.2 kN,频率为20 Hz,应力比为1∶10。实验时,对试样进行分级加载和卸载,配合引伸计(图2b)测量裂纹张开位移,通过裂纹张开位移法获得柔度曲线,微分后得到柔度微分曲线,寻找转折点以确定裂纹闭合临界点即张开载荷Pop。当载荷分别达到0.4,0.6,0.8,1.0,2.8,4.8,8.8 kN时,利用TSC-5M-32型磁记忆检测仪(图2c)配合Type-2M扫描探头(图2d),沿图1所示检测路径采集试件磁信号参数。

(a)MTS-880低频疲劳机 (b)电子引伸计

(c)TSC-5M-32型磁记忆 (d)Type-2M扫描探头 检测仪图2 实验设备Fig.2 Experimental equipments
2 实验结果与分析
2.1 塑性区对裂纹尖端磁场的影响
采用ANSYS中的SMART裂纹扩展程序,对实验中裂纹扩展过程进行有限元仿真,单元选用四面体Solid187单元,两个下支点位置施加垂直方向固定约束,上压头施加低周疲劳载荷,基值8.8 kN、幅值7.2 kN。图3a、图3b分别为裂纹启裂和裂纹扩展至5 mm时的应力云图,红色区域为应力超过材料屈服强度235 MPa的塑性区域。从图3中可以看出,随着裂纹的扩展,裂纹尖端即裂尖周围的塑性区尺寸越来越大,结合图4塑性尾迹原理图可知,裂尖处塑性区尺寸大于裂尾塑性区。

(a)裂纹长度a=0
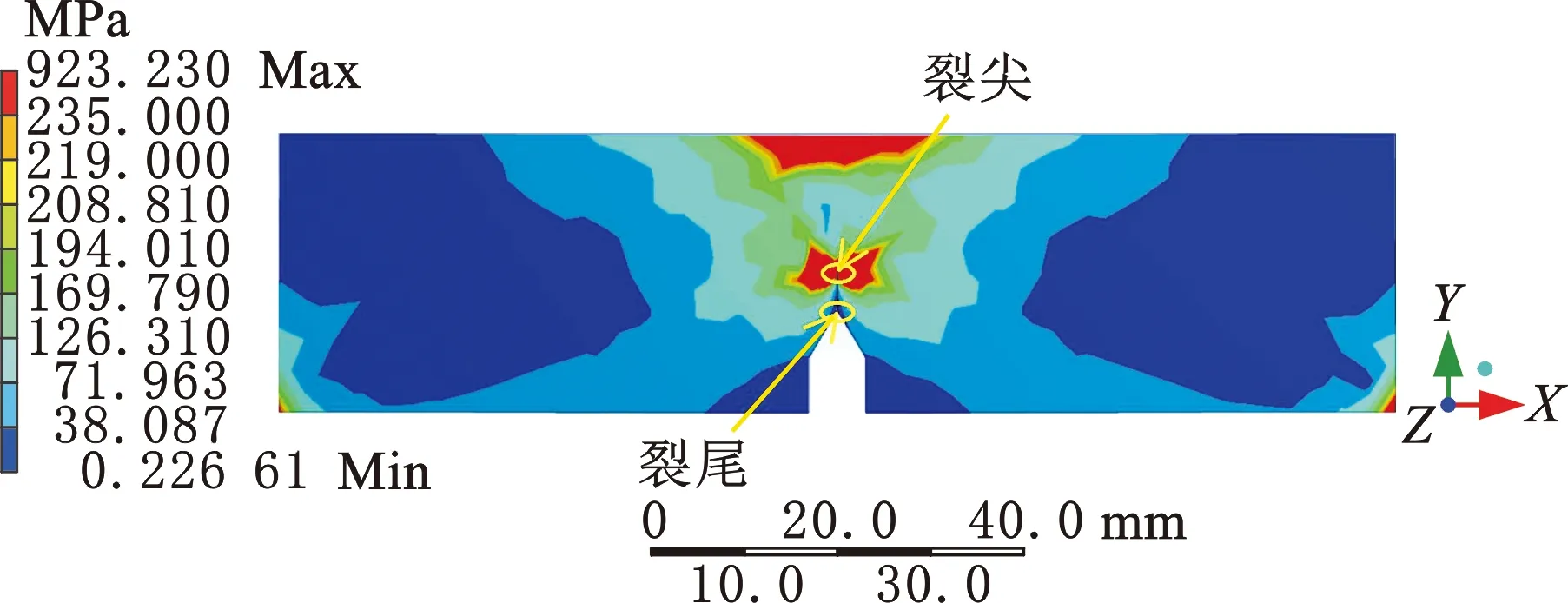
(b)裂纹长度a=5 mm图3 裂纹扩展塑性区尺寸变化Fig.3 Crack extension plastic zone size change
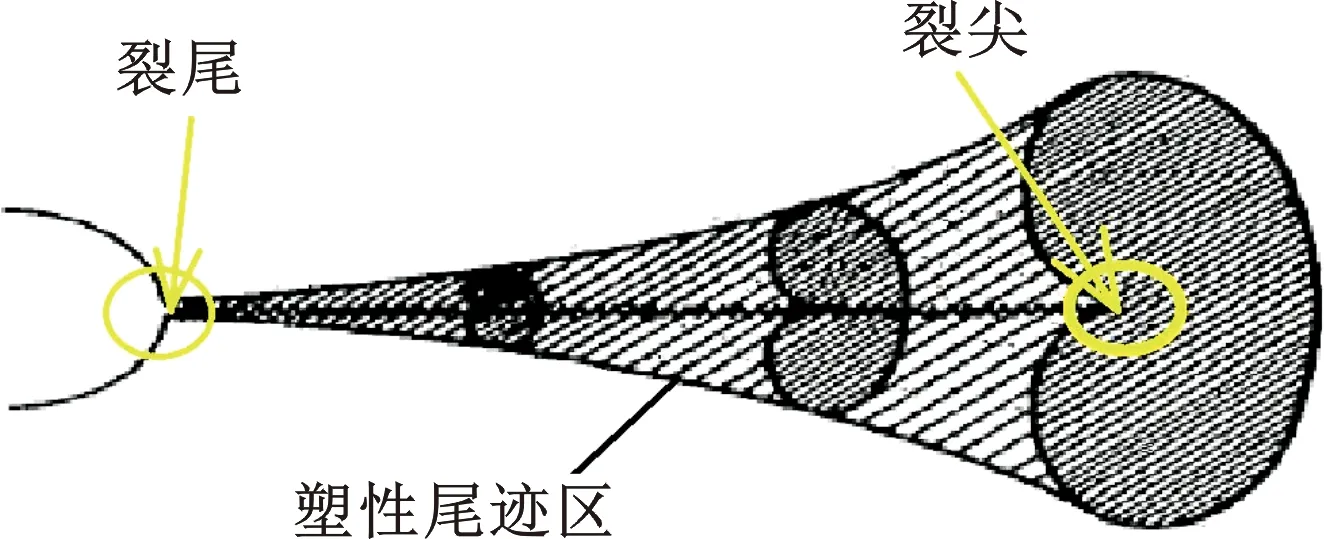
图4 塑性尾迹示意图Fig.4 The plastic wake zone diagram
为进一步研究不同塑性区对磁记忆信号的影响,分别对裂尖和裂尾测试路径进行磁信号采集,如图5所示,结合图3和图4可以看出,裂尖与裂尾塑性区不同,磁信号参数变化也不同。裂纹在扩展过程中,裂尖因应力集中发生小范围屈服,产生裂尖塑性区,裂尖路径磁场法向分量Hp(y)在裂纹区域内存在明显向下的跳变尖点,如图5a所示。由图4可以看出,塑性区随裂纹扩展而增大,同时在裂纹扩展后保留形成塑性尾迹,随着载荷P增大裂尖塑性区增大并且应力发生松弛[16],这导致裂尖处Hp(y)向下跳变的尖点变得越来越平缓。图5b中裂尾路径磁场法向分量Hp(y)随着载荷P呈现整体上移的趋势,在各载荷下曲线形状保持不变,这是由于塑性尾迹周围弹性区对其塑性变形的约束作用,使已开裂的裂纹上下表面由于压应力提前接触,致使磁场信号基本不变。通过对比裂尖和裂尾不同塑性区Hp(y)曲线分布可知,裂尖局部塑性区对磁场信号Hp(y)的影响较大,因此本文重点研究裂尖磁场分量的临界特征。

(a)不同载荷裂尖路径Hp(y)曲线

(b)不同载荷裂尾路径Hp(y)曲线图5 不同载荷对塑性区Hp(y)曲线影响Fig.5 Effect of different loads on the Hp(y) curve in the plastic zone
2.2 裂纹闭合现象的磁场分量变化规律
图6为加载和卸载实验中的柔度曲线及其微分得到的柔度微分曲线。根据裂纹在完全张开后结构的柔度会保持不变,目前国内外常采用以下方法确定张开载荷:通过柔度微分曲线上偏离线性段的转折点(图6)来定位柔度发生变化的临界点,当载荷低于临界点时裂纹闭合[17],本文实验中当载荷达到0.8 kN时柔度微分曲线出现偏离线性段的转折点,从而确定张开载荷Pop为0.8 kN。

(a)加载过程

(b)卸载过程图6 柔度及柔度微分曲线Fig.6 Compliance cuves and compliance differential cuves
图7为裂纹闭合临界载荷示意图,图8为压磁效应示意图,图9为裂纹闭合实验中磁场分量变化曲线。结合图7可以得出,在图9a加载和图9b卸载过程都存在如下情况:当载荷小于0.8 kN临界点时为裂纹闭合状态,裂纹循环塑性区内存在残余压应力,由于压磁效应(图8),磁畴中原子磁矩沿着压应力垂直方向发生偏转,造成裂尖法向分量Hp(y)曲线发生剧烈变化,即向下跳变出现尖点,且随着载荷的增大,裂尖Hp(y)绝对值增大;当载荷大于裂纹闭合临界点0.8 kN时,裂纹完全张开,随着载荷继续增大,塑性尾迹中的塑性区变大,发生应力释放和松弛,向下跳变尖点变平缓,同时裂尖区域Hp(y)绝对值出现减小趋势。图9c和图9d中,加载与卸载过程裂纹区域磁场切向分量Hp(x)出现明显跳变,表明此处裂尖具有较大的应力集中。图9卸载过程与加载过程相比,总体上,由于在加载过程材料经历了较大载荷后,卸载过程中内部损伤、位错以及不可逆的磁畴磁矩偏转已经达到饱和,因而在卸载过程中随着载荷减小,磁信号曲线下降不大。
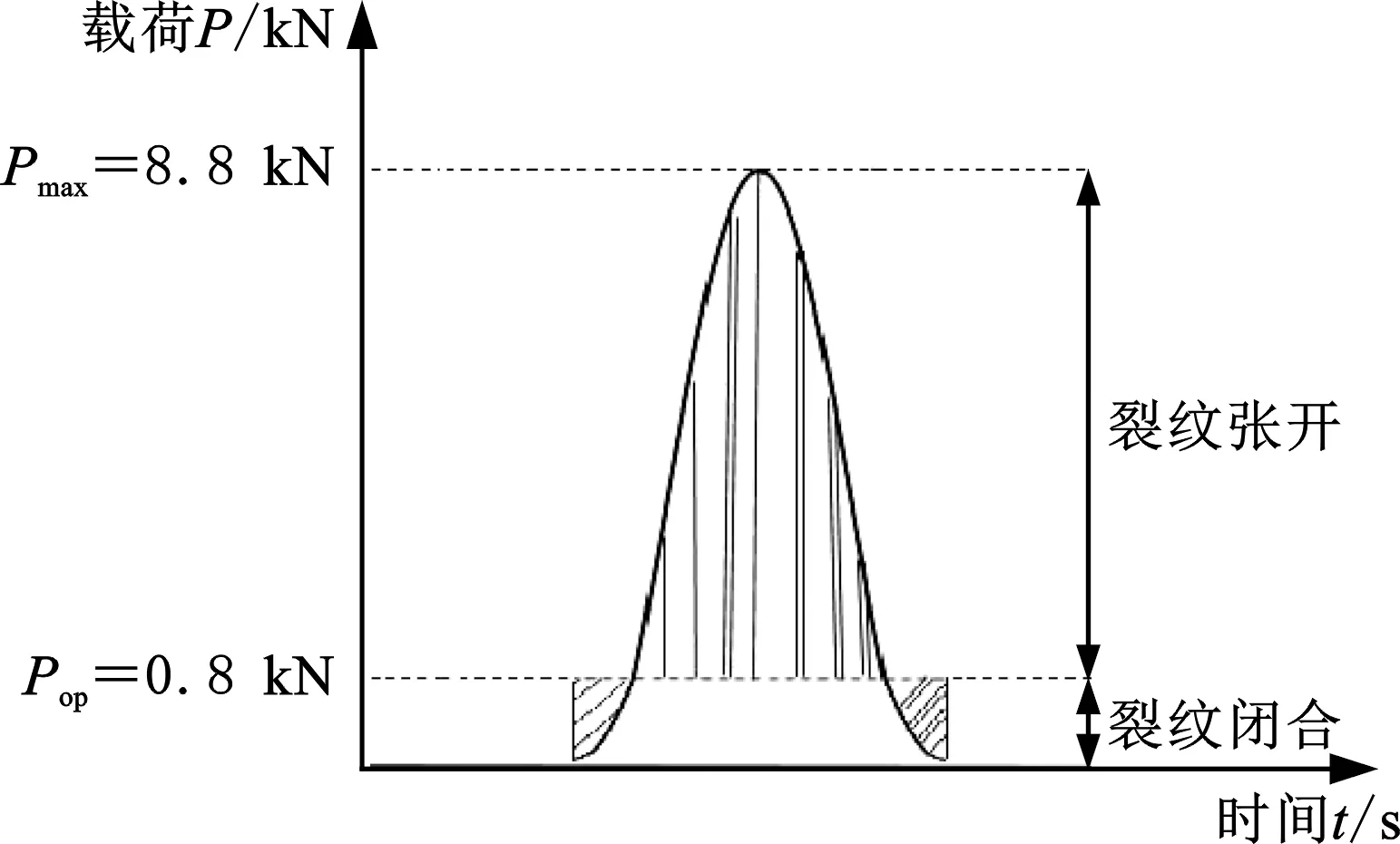
图7 裂纹闭合临界载荷示意图Fig.7 Critical load for crack closure diagram
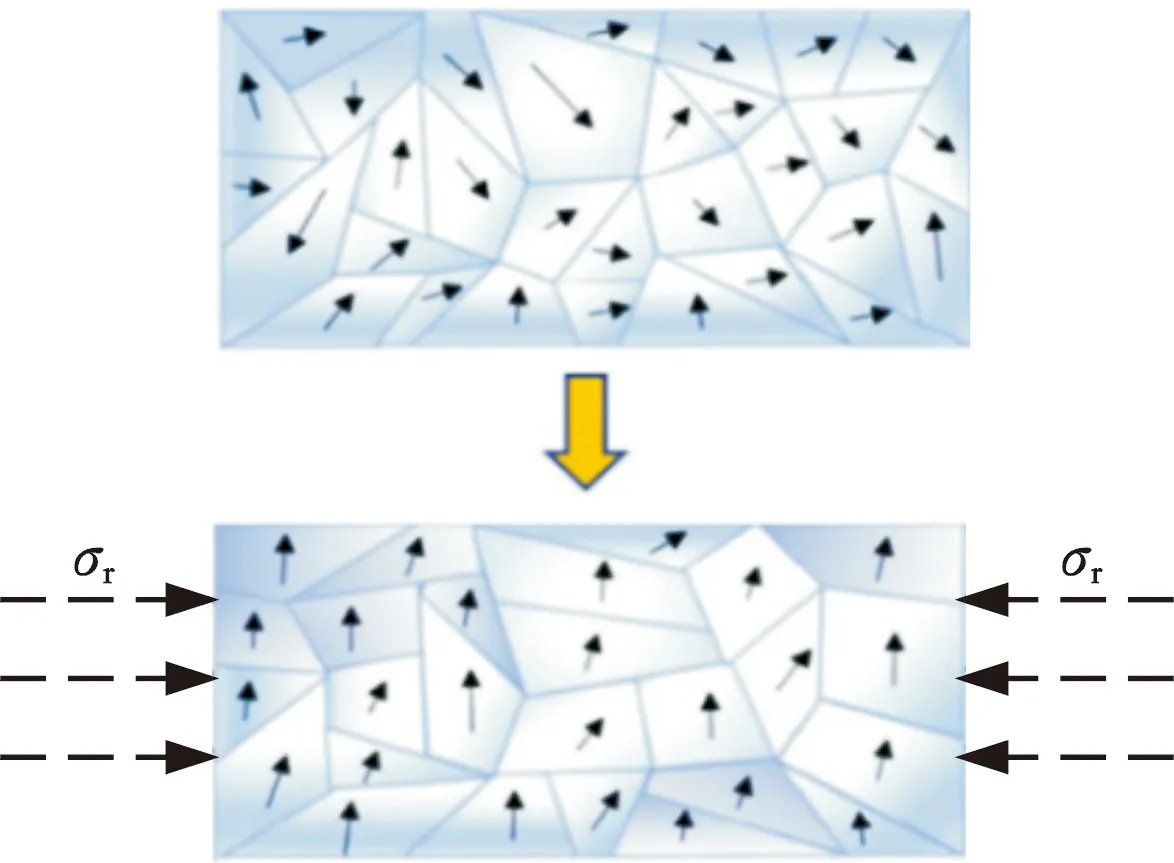
图8 压磁效应示意图Fig.8 Piezomagnetism effect diagram
2.3 裂纹闭合时磁特性参数临界特征
为更好地对裂纹闭合状态进行表征,考虑磁场强度为矢量,在得到磁场法向、切向分量变化规律的基础上,发现加载和卸载的过程中随着载荷的变化,合成磁特性参数ΔHp曲线与柔度微分曲线的变化趋势一致,如图10所示,因此选用合成ΔHp作为磁特性参数来表征裂纹闭合规律,合成ΔHp计算式为
ΔHp=
(1)
式中,Hp(x1)、Hp(x2)分别为x1、x2裂尖附近位置的切向最大磁场强度和最小磁场强度;Hp(y1)、Hp(y2)分别为x1、x2裂尖附近位置的法向最大磁场强度和最小磁场强度。
从图10 a、图10 b中不难看出,当载荷接近Pop=0.8 kN裂纹闭合临界点时,磁特性参数合成的ΔHp在一个较低的水平浮动,并向下跳变出现极小值点,当载荷等于Pop时处于裂纹闭合临界点,柔度微分曲线出现转折点,合成磁特性参数ΔHp产生剧烈跳变,也出现转折点;当载荷高于裂纹闭合临界点Pop之后,裂纹完全张开,随着载荷增大,裂尖区域内的压应力转变为拉应力,合成磁特性参数ΔHp维持在一个较高的水平上下波动。在裂纹闭合临界状态时,合成磁特性参数ΔHp和柔度微分曲线都出现快速变化的转折点,并在载荷大于裂纹闭合临界点时,同时出现高位波动,有较强的相关性,说明磁特性参数测定并用于表征裂纹闭合是合理的。

(a)加载阶段Hp(y)

(c)加载阶段Hp(x)

(d)卸载阶段Hp(x)图9 裂纹闭合实验中裂尖磁场分量变化曲线Fig.9 Variation regularity of magnetic characteristic parameters of crack tip in crack closure experiments

(a)加载阶段ΔHp

(b)卸载阶段ΔHp图10 柔度微分曲线与合成ΔHp对比图Fig.10 Comparison between the compliance differentialcuves and ΔHp
3 基于磁特性参数的裂纹闭合表征模型及验证
由实验可知,合成磁特性参数与柔度微分曲线的变化规律高度一致,因此应用合成磁特性参数表征柔度微分曲线,建立基于磁特性参数的裂纹闭合表征模型,可以突破必须在实验室内采用引伸计测量裂纹闭合临界点的局面,为进一步在工程实际中便捷地判定裂纹闭合状态提供新的方法。根据图10选用合成磁特性参数ΔHp,将裂纹张开位移微分值分别与加载和卸载的合成磁特性参数ΔHp进行回归拟合,见图11。

(a)加载过程磁特性参数拟合
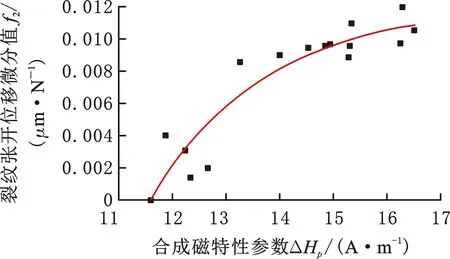
(b)卸载过程磁特性参数拟合图11 裂纹张开位移微分值与磁特性参数拟合图Fig.11 Crack opening displacement differential value and ΔHp fit chart
图11a所示为加载阶段拟合曲线,ΔHp接近裂纹闭合临界点时出现快速增长。结合图10a可知,当载荷达到裂纹闭合临界点时,加载阶段的拟合曲线出现最大值,随后载荷大于裂纹闭合临界值,裂纹完全张开,拟合曲线呈下降趋势,具体模型如下:
(2)
式中,f1(ΔHp)为加载过程中裂纹张开位移微分值,mm/kN。
图11b所示为卸载阶段拟合曲线,ΔHp接近裂纹闭合临界点时同样出现快速增长。结合图10b可知,当载荷达到裂纹闭合临界点时,拟合曲线出现拐点,随后上升趋于平缓,此时载荷大于裂纹闭合临界值,裂纹完全张开,裂纹闭合临界状态特征显著,表征模型如下:
(3)
式中,f2(ΔHp)为卸载过程中裂纹张开位移微分值,mm/kN。
不论加载过程还是卸载过程,拟合曲线的斜率在裂纹闭合临界点前后出现明显改变,拟合曲线很好地表征了裂纹闭合临界状态的变化规律。
为了验证裂纹闭合表征模型的正确性,用相同材质的另一组试件,重复相同的加载、卸载实验,获得裂纹闭合演化过程临界状态的磁特性参数ΔHp以及裂纹张开位移微分值,将磁特性参数ΔHp代入式(2)和式(3),分别获得加载过程和卸载过程中的裂纹张开位移微分值,与实验得到的裂纹张开位移微分值对比,验证结果如图12所示。

(a)加载阶段

(b)卸载阶段图12 表征模型验证图Fig.12 Characterization model validation diagram
对比加载阶段的图12a与图10a可以看出:随着载荷增加,当磁特性参数ΔHp达到裂纹闭合临界点时,裂纹由闭合状态变为裂纹完全张开状态,曲线出现拐点,随后呈下降趋势,实验数据在拐点两侧形成明显的区域聚集。对比卸载阶段的图12b与图10b可以看出:随着载荷减小,当磁特性参数ΔHp达到裂纹闭合临界点时,裂纹由完全张开状态变为裂纹闭合状态,曲线的增长趋势放缓,实验数据在临界点左右同样出现聚集,因此裂纹闭合模型能很好地表征裂纹闭合现象的临界状态,加载阶段模型预测值与实测值最大相对误差为9.398%,卸载阶段模型预测值与实测值最大相对误差为11.549%。
4 结论
(1)对裂纹扩展过程进行有限元仿真分析,发现裂尖塑性区尺寸大于裂尾塑性区尺寸。对比磁场实测数据,分析了不同载荷下裂尖与裂尾塑性区对磁场信号的影响,发现裂尖塑性区对磁场信号影响更大。
(2)实验结果表明:当载荷接近临界点Pop时裂纹闭合,磁特性参数ΔHp向下出现极小值拐点;随后当载荷等于Pop临界点时,ΔHp向上跳变并出现转折点,对比柔度微分曲线也出现转折点;当载荷高于Pop时,裂纹完全张开,ΔHp维持在较高的水平上下波动,ΔHp与柔度微分曲线的变化规律高度一致,因此采用磁特性参数表征裂纹闭合具有合理性。
(3)建立了基于合成磁特性参数ΔHp的裂纹闭合表征模型,可以通过磁特性参数的临界特征对裂纹闭合状态进行判断,验证结果表明加载阶段和卸载阶段的模型预测值与实测值最大相对误差分别为9.398%和11.549%,为工程实际中判断并表征裂纹闭合提供新的思路。
