互补式双层时栅角位移传感器研究

杨继森 付 航 秦梓洋 周 润

重庆理工大学机械检测技术与装备教育部工程研究中心，重庆，400054

0 引言

时栅是一种新型位移传感器，其核心思想是利用时间量完成空间量的描述。时栅角位移传感器规避了传统栅式位移传感器的测量精度受限于刻线精度的弊端，并且具有高精度、智能化、使用方便等特点，被广泛应用于航空航天、国防军工、数控机床等领域[1-5]。

目前，基于印刷电路板(PCB)工艺研制的时栅角位移传感器克服了传统线槽式时栅角位移传感器制造工艺复杂、生产效率较低、成本高等不足。但是，当前研制的基于PCB工艺的传感器线圈依然存在感应信号较弱、时变磁场的有效利用率较低、驻波幅值不完全相等不足，导致误差曲线中出现较高的4次谐波[6-10]，降低整个传感器电气系统的信噪比，影响传感器的测量精度与抗干扰性能。针对上述情况，结合时变磁场的电磁感应原理和时栅位移传感器理论[11-12]，对原有双层时栅角位移传感器机构进行优化改进，提出了一种新型的互补式双层时栅角位移传感器的设计方案。该方案在一定程度上解决了双层时栅角位移传感器在生产时由于PCB加工工艺不同而导致测量误差规律不同的问题，提高了传感器的精度。

1 传感器模型及信号感应原理

互补式双层时栅角位移传感器结构如图1所示。该传感器结构分为激励和感应两部分，均采用了双层互补式结构，实现对磁场的约束和拾取能力的相互补偿。图1b所示为传感器感应线圈，线圈由四路正弦形状的线圈相互交错而成，相邻两线圈结构相位差为180°以实现差分输出，并且在结构上采用了上层线圈与下层线圈分别对称的形式，使传感器对磁场两端的利用率尽可能相同，以保证感应线圈能够充分拾取有效磁场。图1c所示为传感器感应线圈与激励线圈的基体，线圈基体有利于线圈对磁场的约束作用。图1d所示为激励线圈，线圈交替绕制而成，每组正(余)弦对极数均为20，并且错开四分之五个空间节距以实现空间上正交上下层分布且错开四分之一节距的正余弦结构，相同角度上的矩形激励线圈之间在传感器半径上呈对称分布，这种互补结构可以使同一半径上，线圈两端对磁场的约束能力相互补偿，让磁场分布更加均匀。

(c)传感器基本模型 (d)激励线圈模型图1 互补式双层时栅角位移传感器整体模型Fig.1 Integral model of complementary double-layer time-grid angular displacement sensor

由于传统双层时栅角位移传感器的激励线圈采用下层通入正弦信号、上层通入余弦信号的方式，导致两路激励线圈到感应线圈的距离不同，因此在同一感应线圈拾取到正余弦信号产生的磁场强度不同，影响行波质量。分块状正余弦线圈结构在同一平面产生激励信号可有效地避免这一不足。为了能够更好地形成驻波，在激励线圈中分别通入频率为ω、幅值为A的两路电流ia=Asinωt与ib=Acosωt作为激励信号以实现时间上的正交。

传感器单个极距基本结构如图2所示。图2a所示为单个极距的整体结构，图2b中沿箭头方向从左到右分别为底层激励线圈、上层激励线圈、上层感应线圈和底层感应线圈。

(a)整体模型 (b)线圈模型图2 互补式双层时栅角位移传感器的单极距解剖图Fig.2 Anatomic diagram of a complementary double-layer time-grid angular displacement sensor with single-pole distance

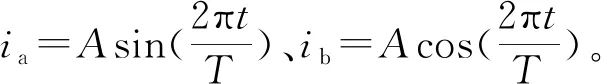
(1)

式中，Φ1、Φ2、Φ3、Φ4为磁通量；K1、K2、K3、K4为信号幅值；W为线圈空间节距；θ为感应线圈旋转的角度值。

由信号叠加原理得到总的输出感应电动势为

(2)

2 参数设置及结构分析

2.1 双层时栅位移传感器磁场分布模型

根据式(2)可知，K值影响了感应线圈输出电动势大小，采用双层互补式激励线圈虽然有效增加了时变磁场的整体强度，增大了有效磁场的区域，但实际应用时存在上下层线圈之间间距过大使叠加效果不明显、过小产生磁场串扰等问题。

根据建立的双层时栅角位移传感器激励模型(图3)，假设在双层线圈中分别通电流I+和I-，对磁场进行分析，根据毕奥-萨伐尔定律，可以得出空间任意点N(x，y，z)的磁场强度。

图3 双层线圈的磁场计算模型Fig.3 Magnetic field calculation model of double coil

空间任意点N的磁场强度由上下两U字形共6段有限长通电直导线BC、CD、DA、A′B′、B′C′、D′A′产生的磁场强度叠加而成。以BC段为例分段计算，在BC段取电流元dl，BC段在N点处的磁感应强度是电流元dl在该点的磁感应强度沿BC积分的结果[13-14]，其计算表达式为

(3)

式中，μ0为真空磁导率；I为电流。

从图3中可得出如下关系：

l=H/tanθ|MN|=H/sinθ

(4)

(5)

式中，H为点N到BC的最短距离。

联立式(4)可将式(3)化简为

(6)

双层时栅角位移传感器的激励线圈和感应线圈平行(所在平面)，且感应线圈相对激励线圈运动，只需考虑垂直于线圈所在平面的磁场感应强度分量即沿Z轴分布的磁感应强度分量BBCZ，计算表达式为

(7)

同理可求出BCDZ、BDAZ、BA′B′Z、BB′C′Z、BD′A′Z，由磁场叠加原理，有

BZ=BBCZ+BCDZ+BDAZ+BA′B′Z+BB′C′Z+BD′A′Z

(8)

因此，可求得BZ为

(9)

2.2 双层激励线圈间距仿真

对激励线圈的间距进行仿真，具体仿真参数如表1所示。

表1 激励线圈基本参数设置

将单个对极的扇形线圈等效为高40 mm、宽3π/8 mm的矩形，以4层PCB的距离参数为变量进行仿真，结果如图4～图7所示。图4所示为单层U形线圈磁场分布，磁感应强度约为1.97×10-8T；图5所示为间距0.235 mm的双层互补型线圈磁场分布，磁感应强度约为2.59×10-8T；图6所示为间距1.335 mm的双层互补型线圈磁场分布，磁感应强度约为2.66×10-8T；图7所示为间距1.6 mm的双层互补型线圈磁场分布，磁感应强度约为2.55×10-8T。

图4 单层U形线圈磁场分布Fig.4 Magnetic field distribution of single layer “U” coil

图5 双层互补线圈间距0.235 mm磁场分布Fig.5 Magnetic field distribution with double-layer complementary coil spacing of 0.235 mm

图6 双层互补线圈间距1.335 mm磁场分布Fig.6 Magnetic field distribution with double-layer complementary coil spacing of 1.335 mm

图7 双层互补线圈间距1.6 mm磁场分布Fig.7 Magnetic field distribution with double-layer complementary coil spacing of 1.6 mm

由图4～图7可知，单层U形线圈有较强的端部效应，当激励线圈的间距为1.335 mm和1.6 mm时，有较小的端部效应，导致Y方向上磁场分布不均匀。当激励线圈间距为0.235 mm时，基本无端部效应，产生的瞬时磁场强度较大，且磁感线分布均匀度较高。

不同间距下的互补式双层激励线圈结构的磁场强度比较结果如表2所示。

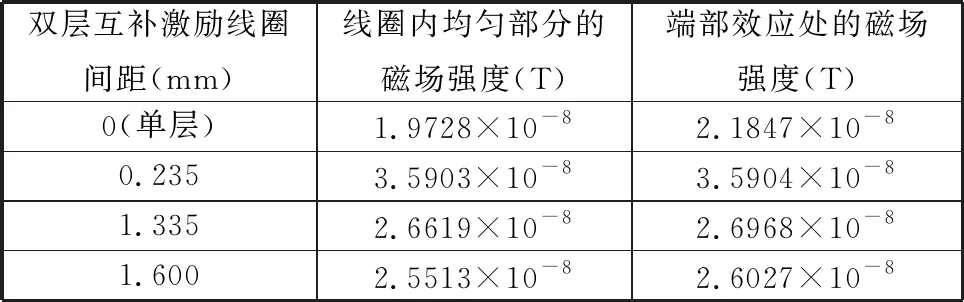
表2 双层激励线圈不同间距下的磁场强度

3 有限元仿真分析

3.1 模型建立及参数设置

平面感应线圈的感应信号质量问题是磁场式角位移传感器的研究重点，时栅传感器位移解算的鉴相方式决定了感应电动势输出必须呈正弦式变化且幅值尽可能大，输出电动势的质量将直接影响传感器测量精度。根据式(2)，假设含有误差的感应电动势表示为

(10)

式中，P为谐波带来的测量误差的相位值。

在电磁相互转换的过程中要求线圈内部磁感应分布中的基波所占成分尽可能大，将含有误差的感应电动势呈傅里叶级数展开可得

(11)

式中，A0为直流分量；Ai为谐波幅值；φi为谐波初相角度。

将基波幅值提出，求得谐波所占总量的百分比，谐波所占百分比越小代表其输出感应信号的质量越好，用谐波畸变率表示[15]：

(12)

由第2节对双层时栅位移传感器平面线圈的磁场理论分析知，新型双层时栅角位移传感器结构为分块式，结合具体参数对传感器建模，得到图8所示的模型。

(a)激励线圈 (b)感应线圈

(c)整体模型
图8 互补式双层时栅角位移传感器仿真模型
Fig.8 Simulation model of complementary double-layer time-grid angular displacement sensor

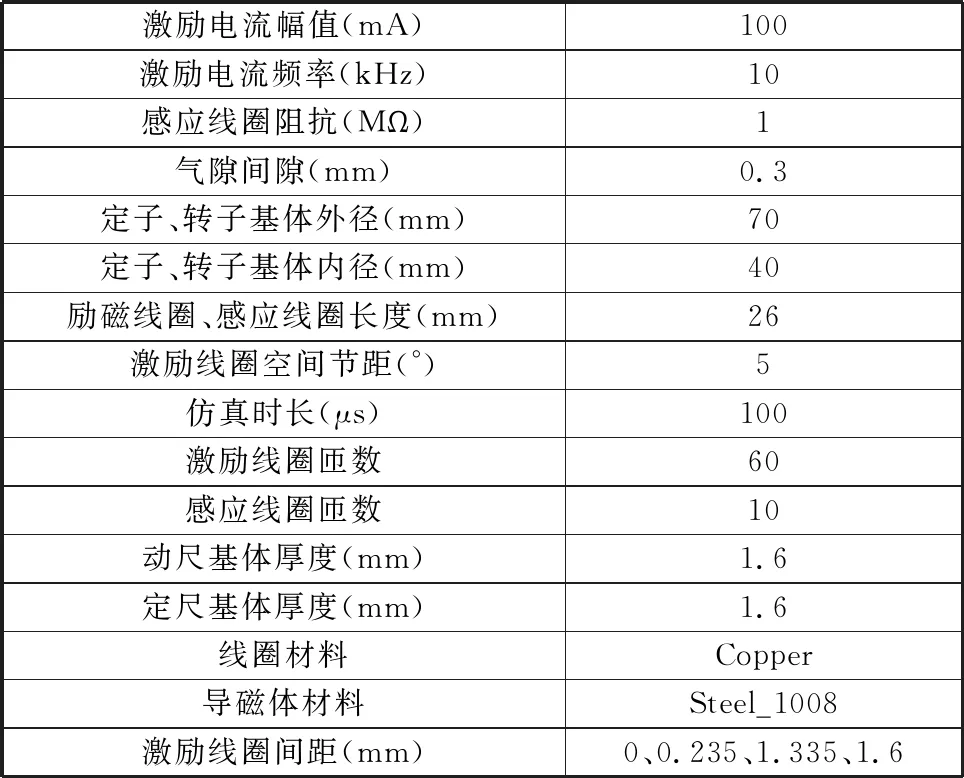
表3 仿真模型参数设置

在整个仿真过程中，设置四路激励电流分别为：0.1sin(2000πt)(A)、-0.1sin(2000πt)(A)、0.1cos(2000πt)(A)、-0.1cos(2000πt)(A)，仿真步长为0.2°，采样间隔为2 μs，保证每条线呈现出线性关系。同时固定定子，使转子沿着顺时针方向运动一个节距(5°)，观察分析行波和驻波的各参数状态。

3.2 仿真数据及分析

双层激励线圈内通入正弦激励信号0.1 sin(2000πt)(A)、-0.1sin(2000πt)(A)，设置激励线圈间距为0.235 mm，感应线圈沿逆时针方向运动，根据第1节双层位移时栅传感器的电磁感应原理，正弦线圈拾取磁场后加载到内圈上下两路和外圈上下感应线圈输出信号如图9a所示。同理，分别通入余弦激励0.1cos(2000πt)(A)、-0.1cos(2000πt)(A)，感应线圈输出信号如图9b所示。由图9可知，两驻波呈时间轴对称，幅值约470 mV，驻波零点固定，其余点周期性上下波动，输出波形符合电磁感应定律。

(a)通入正弦激励信号 (b)通入余弦激励信号图9 驻波仿真图Fig.9 Standing wave simulation diagram

通入电流0.1sin(2000πt)(A)、0.1cos(2000πt)(A)作为激励信号，有限元仿真结果如图10b所示，该输出信号由四路感应信号叠加而成，行波幅值约为472 mV，整个周期幅值、间距较均匀。改变双层时栅角位移传感器激励线圈间距参数为0 mm，得到行波信号如图10a所示，改变间距参数为1.235 mm得到行波信号如图10c所示，改变间距参数为1.6 mm得到行波信号如图10d所示。传感器输出行波需速度恒定、空间间隔均匀且波形固定，因此要求行波信号在时间坐标轴上等间距分布，且峰-峰值稳定。

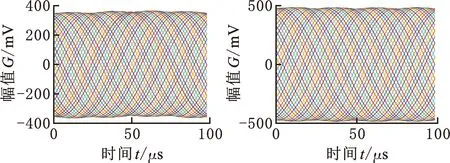
(a)单层(间距为0) (b)双层(间距为0.235 mm)

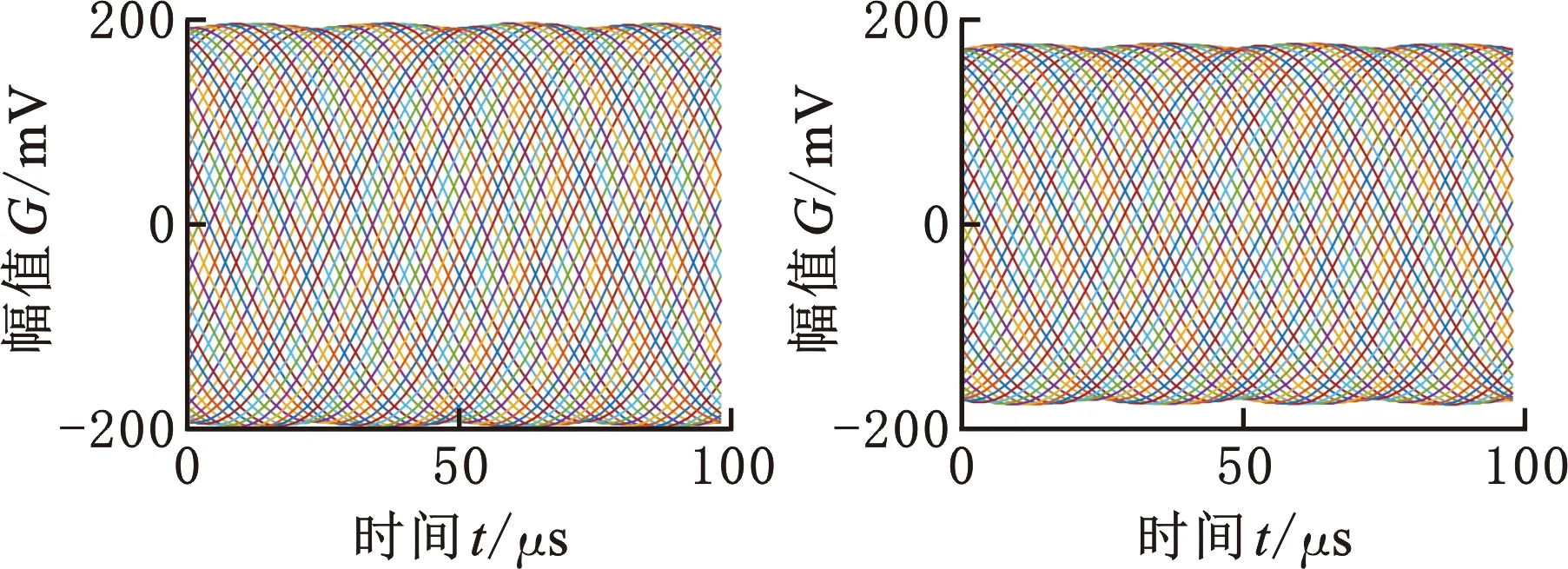
(c)双层 (d)双层 (间距为1.335 mm) (间距为1.600 mm)图10 行波仿真对比Fig.10 Comparison of traveling wave simulation

由图10仿真结果可知：单层矩形激励线圈产生的感应电动势较大，但感应电动势幅值不稳定，且在时间轴上分布不均匀；当双层激励线圈间距为0.235 mm时，行波分布较均匀且幅值稳定在490 mV左右；随着激励线圈的间距逐渐增大，端部效应导致的感应电动势幅值误差稳定性差，行波在时间轴上的分布更加不均匀。

根据3.1节，谐波畸变率可反应感应电动势信号的质量，其值越低，表明感应信号的质量越高。将Maxwell导出的所有点数据存为.csv格式文件，得到从0°～5°的50条正弦曲线。取图10中间时刻(t=50 μs)上0°～5°各电压值观察整个空间节距上的分布，如图11所示。当感应线圈为单层时，感应电动势峰值为370 mV；当激励线圈间距为0.235 mm时，感应电动势峰值最大，在整个节距上各个点电压值呈现出正弦周期变化且分布均匀，在波峰处光滑，符合标准正弦波；感应电动势幅值和平滑程度随着激励线圈间距的增大而降低。通过式(12)得到各不同间距的谐波畸变率，如图12所示。

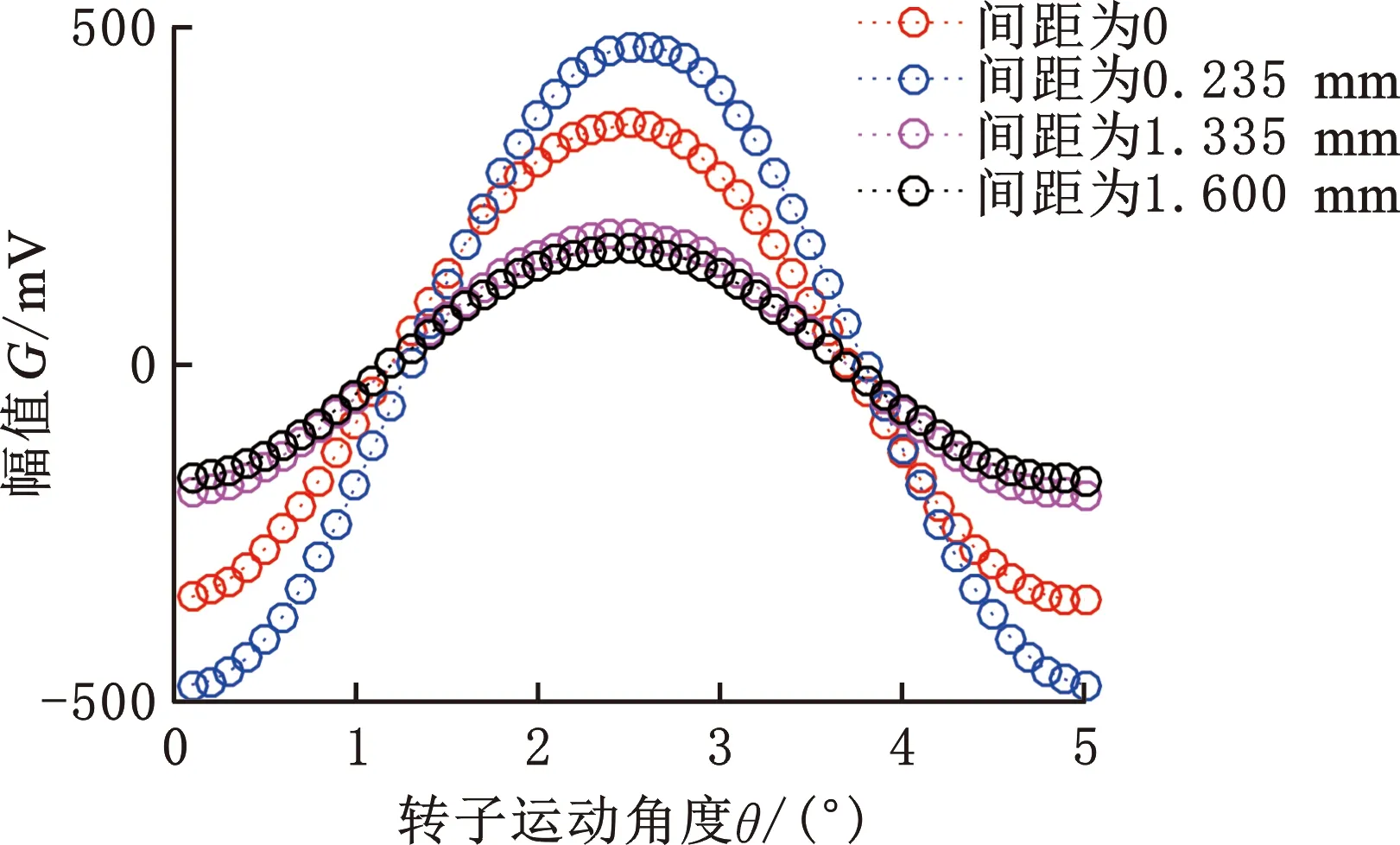
图11 传感器在50 μs时刻感应信号的幅值Fig.11 The sensor detects the signal amplitude at 50 μs

图12 不同间距设置下传感器的谐波畸变率Fig.12 The harmonic distortion rate of the sensor under different clearance Settings

为进一步观察不同间隙带来的误差，提取每一时刻波形的初相位，与理想位移值作比较，根据每一个时间周期内的基波幅值与初始相位值得到的误差曲线见图13，图中纵坐标为相位移量。

图13 双层激励线圈不同间隙下的误差曲线Fig.13 Error curves of double-layer excitation coils with different gaps

由图13可知，4种状态下，一个节距内(0°～5°)误差呈现周期性分布。单层激励线圈的误差曲线表示范围为(-80.4″，50.3″)；双层激励线圈间距为1.335 mm时的误差曲线范围为(-29.5″，21.75″)；随着间距增加，误差曲线峰-峰值逐渐增大。

根据2.1节对线框磁场分布的数学模型分析可知，端部效应导致单层激励线圈产生的磁场在感应线圈拾取的感应电动势信号误差偏大，而激励线圈间距为0.235 mm时可较大程度上耦合端部效应带来的磁场不对称，但随着间距的增大，端部效应渐趋明显，因此误差呈现逐步增大的趋势。

为了进一步分析误差来源，将误差曲线进行傅里叶分析，并且比较传感器激励线圈不同间距时谐波成分的幅值，结果如图14所示。

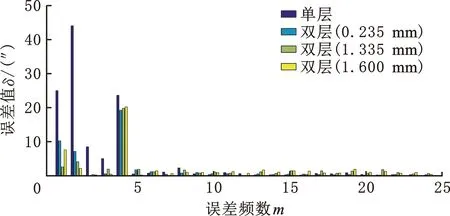
图14 不同间距下传感器仿真误差的谐波分析Fig.14 Harmonic analysis of sensor simulation error under different clearance

为能够更好地对比分析，取前10次误差谐波幅值，如表4所示。

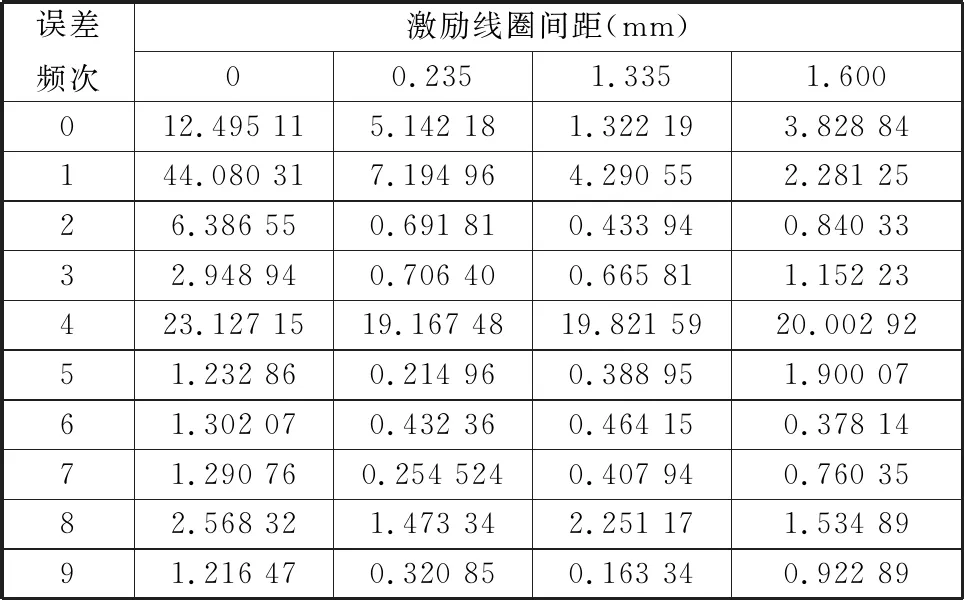
表4 仿真误差谐波成分

由图14和表4观察可知：采用单层U形激励线圈的误差曲线中主要存在1次谐波和4次谐波；采用双层互补结构较大地减小了误差曲线的1次谐波，一定程度上减小了4次误差谐波；随着双层互补型时栅角位移传感器的激励线圈间距从0.235 mm增大，4次谐波呈现上升趋势，1次谐波呈下降趋势。

经过对比分析，双层时栅角位移传感器激励线圈的优化主要减小了传感器误差的1次和4次谐波大小，并且该谐波受间距参数的影响，间距越大1次谐波逐渐越小，同时4次谐波和其他谐波频次伴随增大，但增幅不明显。

4 实验验证与分析

4.1 实验平台搭建

根据上述优化模型，完成对时栅传感器的设计。根据设计经验，尺寸太小线圈精度会严重受限于PCB布线精度，并且由栅式位移传感器的多测头平均效应可知，正弦周期数越多传感器测量感应信号均化程度越高，但布线太密集同样受限于PCB布线精度，结合原双层时栅角位移传感器尺寸，将传感器内径和外径分别设置为40 mm和70 mm，正弦周期个数为72，线宽设置为0.254 mm(10 mil)，如图15所示。

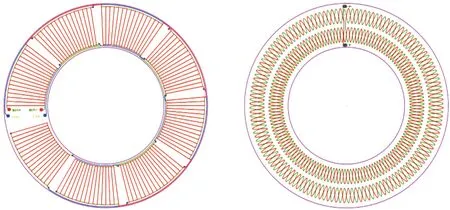
(a)激励线圈样机 (b)感应线圈样机图15 互补式双层时栅角位移传感器的PCB样机示意图Fig.15 Schematic diagram of PCB prototype of complementary double-layer time-grid angular displacement sensor

实验平台搭建在25 ℃恒温环境、无噪声振动、35%恒定湿度环境的超精密实验室。图16所示为嵌入式时栅角位移传感器实验系统，整个实验平台包括大理石实验平台、转子升降控制器、电气系统、上位机、电机驱动器、圆光栅等。

图16 互补式双层时栅传感器实验系统Fig.16 Experimental system of complementary double-layer time-grid sensor

4.2 对比实验与分析

为了验证双层时栅位移传感器的有效性，对传感器模型进行了实验分析。通入10 kHz正余弦信号作为激励源，以精度为±0.8 ″的海德汉RON-886型角度编码器作为基准对双层时栅传感器进行标定。感应线圈与上层激励线圈的距离一定，设置传感器采样点数为100，分别测试单层U形线圈和间距分别为0.235 mm、1.335 mm、1.6 mm的双层激励线圈，提取第三个对极采样点，得到不同间距设置下误差曲线，见图17。

图17 实验误差曲线对比Fig.17 Comparison of experimental error curves

实验结果表明，双层时栅角位移传感器中激励线圈在一定程度上减小了单层U形线圈所带来的误差，并随着双层激励线圈之间距离的增大，误差峰-峰值相应增大，实验结果与仿真结果一致。为了更清晰地分析实验数据，取各误差曲线的1次谐波与4次谐波进行对比分析，结果如表5所示。

表5 实验误差谐波成分

由表5可知，当双层激励线圈的距离为0.235 mm时，误差中4次谐波误差和1次谐波误差最小。实验结果和仿真结果基本相同。

由实验分析可知，双层时栅角位移传感器互补结构的耦合关系能较大程度上抵消磁场中的端部效应所带来磁场分布不对称引起的误差，且受激励距离的影响，耦合关系随间距的增大而减小，与理论分析的结果相吻合。

4.3 误差修正

对双层时栅角位移传感器进行整周期测量与短周期测量对比实验。选定传感器的激励线圈间距0.235 mm，用角度编码器对传感器第三个短周期较大的误差频次进行修正，回转轴再次测量得到数据如图18所示。由图18可知，修正前传感器误差曲线中主要含有1次与4次谐波，修正后传感器的误差曲线中含有少量因随机误差引起的高次谐波。传感器短周期原始误差范围为(-13.61″，13.30″)，修正后误差范围为(-3.01″，0.78″)。

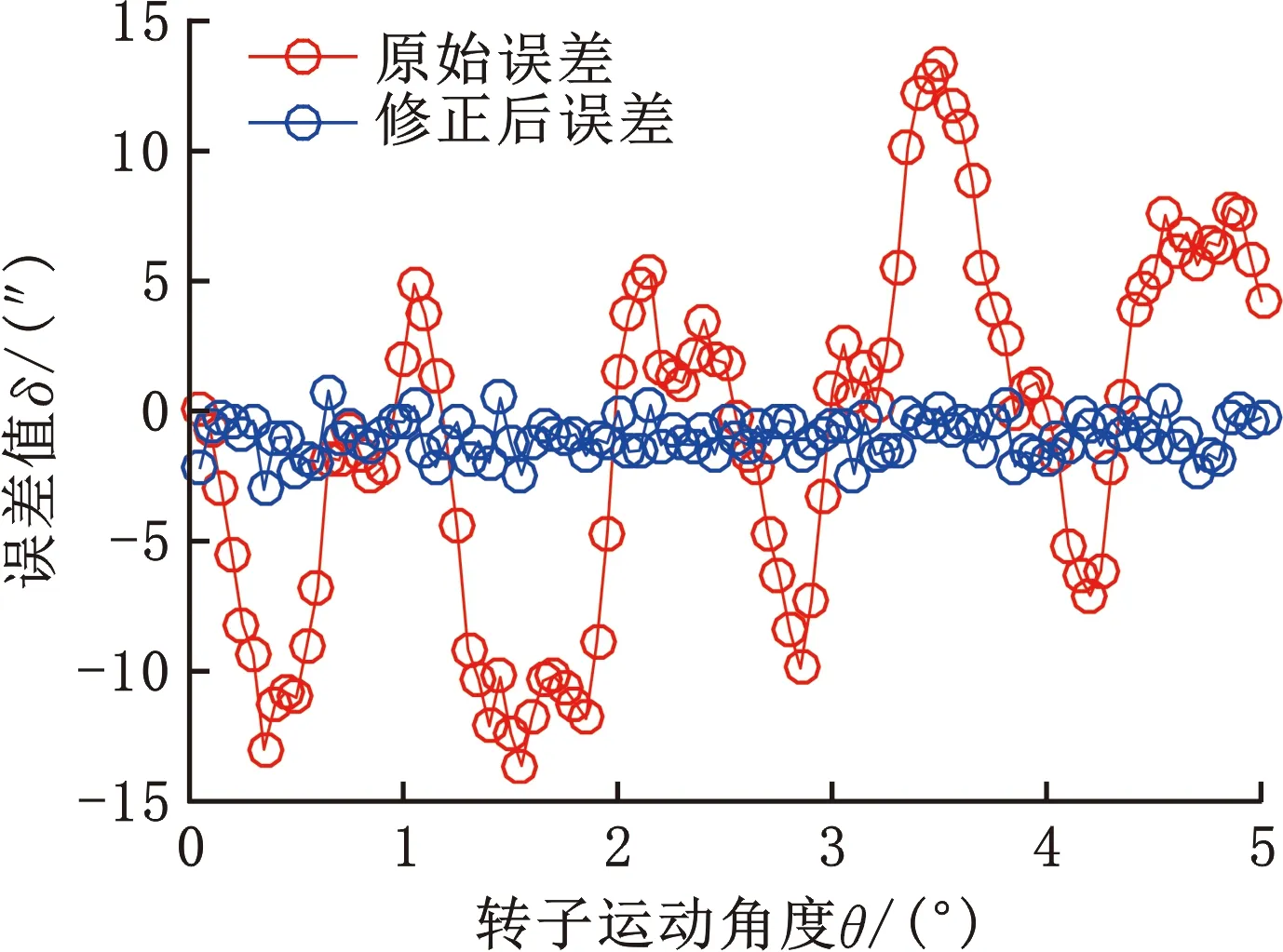
图18 修正前后的误差曲线对比(短周期)Fig.18 Comparison of error curves before and after correction (short cycle)

对整周期误差主要频次进行修正，回转轴再次测量得到数据如图19所示。由图19可知，传感器长周期误差曲线含有较高的1次谐波，且每个对极内短周期误差呈现重复性周期变化，其中1次谐波主要由安装误差引起，传感器原始误差范围为(-19.60″，21.96″)，修正后误差范围为(-2.62″，3.30″)。

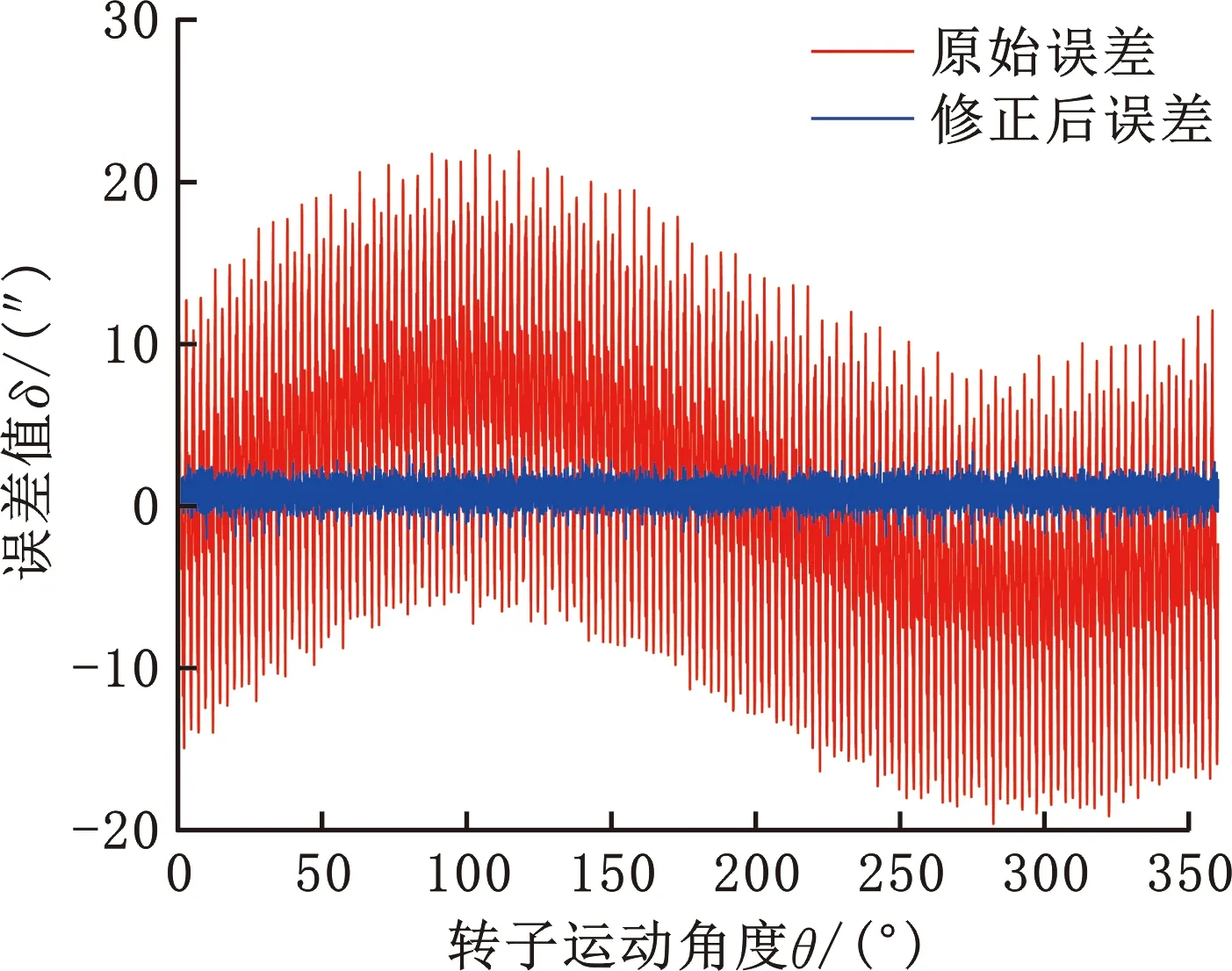
图19 修正前后的误差曲线对比(长周期)Fig.19 Comparison of error curves before and after correction (long cycle)

短周期误差曲线包含的1次和4次误差谐波对误差曲线的影响较大，修正后误差峰-峰值已大幅度降低。而整周期存在较大的1次误差谐波以及实验过程中各种微小的随机误差，对整周期误差修正后能得到较理想的数据。

5 结论

双层互补式时栅角位移传感器增大了感应信号的幅值，并且因其互补结构减小了短周期内1次和4次误差谐波。本文通过数学分析、模型建立、仿真等方法，在原有基础上提供了一种对称式互补双层时栅角位移传感器设计方案，同时通过仿真和实验验证了双层时栅角传感器能够大幅度减小由于端部效应等问题所带来的1次谐波误差和4次谐波误差，提高了传感器精度。根据本研究方案所设计的双层时栅角位移传感器在其针对性误差修正后，短周期测量误差为(-3.01″，0.78″)，长周期误差为(-2.62″，3.30″)。

本研究为双层时栅位移传感器的研究提供了一种有效方案，该方案解决了实际应用中，由于传感器PCB加工工艺差异而产生的测量误差不一致，进而增加了误差修正难度等问题，同时进一步满足了数控加工、精密制造等领域上对传感器精度的需求，具有重要的工程意义。