新型碟式太阳能聚光器跟踪机构优化设计

2023-03-11刘繁茂廖灿灿张原愿

中国机械工程 2023年4期

刘繁茂廖灿灿张原愿莫寒

湖南科技大学机电工程学院，湘潭，411201

0 引言

随着化石能源的日益枯竭和环境问题的日渐严重，太阳能以其储量的无限性、存在的普遍性以及经济性等优势，成为人类亟待大力发展的替代能源。目前，太阳能收集系统主要有碟式、槽式、塔式和光伏等系统[1-2]，其中碟式太阳能发电系统具有结构紧凑、聚光效果好、光热转换率高等优点，被认为是发展空间最大的一种[3]。在碟式太阳能发电系统领域，美国、德国以及中国等国家取得了大的进展，如美国的McDonnelln Douglas系统[4]、德国的EuroDish系统[5]、中国湘电集团研制的38 kW聚光装置[6-7]等，上述碟式太阳能发电系统采用双轴跟踪式。双轴跟踪机构主要是基于串联机构设计的，竖直转轴作为方位驱动装置完成太阳方位角的跟踪，水平转轴作为俯仰驱动装置完成太阳高度角的跟踪。由于竖直转轴固定在地面，承担整个跟踪系统的质量，导致末端驱动装置的负载较大，且能源消耗巨大。此外，由于竖直转轴和水平转轴采用串联的传动方式协同运动，太阳方位角和太阳高度角的跟踪误差相互累计，加上风沙等外载荷的影响，因此跟踪系统的精度保持性较差。针对传统碟式太阳能跟踪系统存在的能耗大和跟踪精度保持性差等问题，部分研究人员采用并联机构作为碟式太阳能发电系统的跟踪机构。于振洋等[8]提出了一种具有驱动冗余的并联式太阳能聚光器跟踪机构，该装置具有刚度高和能耗低的优点。WU等[9]基于U-3PSS机构设计了新型碟式太阳能跟踪装置，具有较大的工作空间和低能耗的优势。并联机构作为碟式太阳能发电系统的跟踪装置，可以实现反射镜的多维运动，与太阳的视日轨迹更加吻合，能够充分吸收转换太阳能，有效解决装置提高发电效率、结构复杂等问题。

本文提出一种动、定平台为任意三角形的通用3-RPS并联机构，基于该机构设计了一种新型碟式太阳能跟踪平台，与双自由度跟踪装置相比，3-RPS并联机构具有1个移动和2个转动自由度，完全能够实现太阳的视日跟踪，最大化地收集太阳能，文献[10-14]均为基于并联机构设计的太阳能跟踪装置。3-RPS并联机构包括3个驱动支链，各驱动支链相互独立，共同改变作为末端执行器的聚光器镜面单元的位姿，实现太阳位置的跟踪，无累计误差且负载分担给多个分支，相同负载下的聚光器具有更好的刚度和稳定性，同时结构紧凑、安装灵活；该跟踪平台的聚光器由传统碟式聚光器改进而来，可以采用已有的旋转抛物面聚光器，且它既可采用双曲面聚光器，又可采用椭圆面聚光器，减少了镜面设计制造和安装调试的费用。从控制上看，单块聚光器镜面单元具有单独的跟踪装置，控制器相互独立，若跟踪误差导致聚光器镜面单元的法线发生偏移，可自动补偿跟踪误差，调整聚光器镜面单元的位姿，从而达到自适应的目的。

并联机构结构参数优化的方法很多，如遗传算法[15]、粒子群算法[16-17]、空间模型法[18]等，本文针对太阳能跟踪装置的设计与应用要求，定义全域灵巧度性能指标、全域刚度性能指标、全域承载能力性能指标，采用线性加权法实现结构参数尺度优化，最终确定一组综合性能较优的几何结构参数，并采用ANSYS有限元软件证明了该参数下太阳能跟踪装置的各项性能指标均有一定程度的提高。

1 新型碟式太阳能聚光器结构设计

图1所示为所设计的新型碟式太阳能聚光器，由光学镜面组件、跟踪机构、辅助电机设备等组成。其中跟踪机构主要由动平台、新型被动球铰链、驱动装置、转动副、定平台组成。考虑到聚光器的制造、运输、安装等过程，注重聚光器镜面单元的模块化设计，在本设计中，抛物面反射镜分成相同5块镜面，镜面方程可表示为x2+y2=4fz，其中f为碟式抛物面聚光器的焦距。接收器安装在焦点处，Φ为镜面的开口直径。动平台作为安装单块镜面的背板，安装在碟式聚光镜的相切基准平面上，聚光器镜面单元之间留有足够的间隙以防止发生干涉和减少风载荷的影响。由于聚光器镜面单元的排布设计，动、定平台形状采用构型为“上大下小”的相似等腰三角形，与定平台连接的转动副、驱动装置、与动平台连接的球副共同组成RPS支链(R、P、S分别为转动副、移动副、球副)，则此新型碟式太阳能聚光器的单个跟踪机构的原型为3-RPS并联机构(图2)。

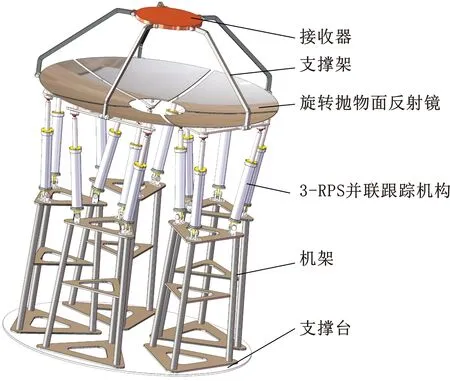
图1 新型碟式太阳能聚光器Fig.1 The new type dish solar concentrator

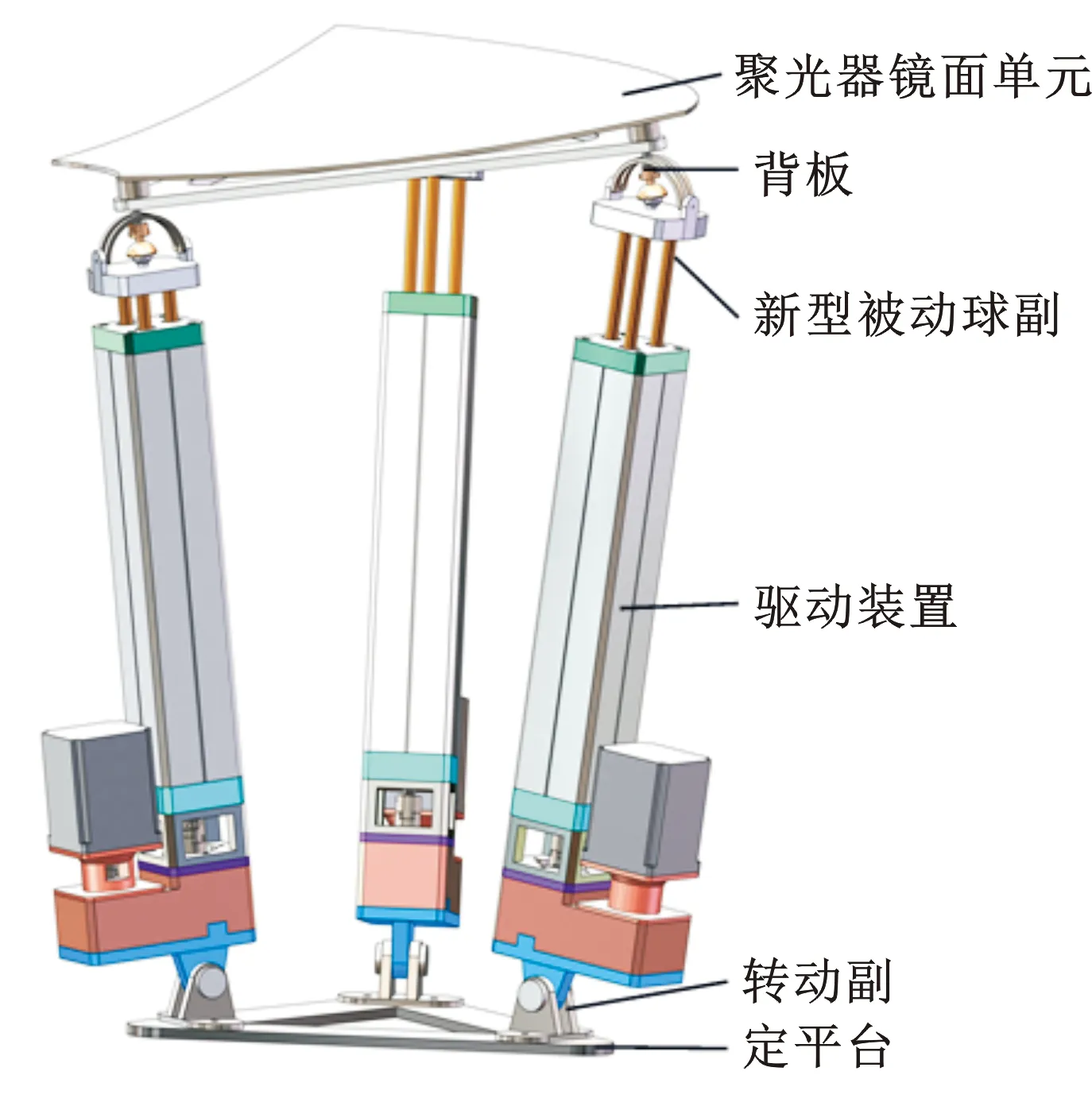
图2 单个跟踪机构示意图Fig.2 Schematic diagram of single tracking mechanism

为提高并联跟踪机构的刚度，提出一种改进型RPS支链，主要由旋转电机、同步带传动组件、滚珠丝杠副、新型被动球铰等组成，如图3所示。滚珠螺母置于滑动活塞内，旋转电机与滚珠丝杠之间通过同步带传动连接，将电机的旋转运动转换为滑动活塞在滑杆外套内的直线运动。滑杆通过螺钉固定在滑动活塞上，在跟踪过程中承载着镜面和动平台的质量，此时力主要沿RPS支链方向，采用均匀分布的3根滑杆负载，提高3-RPS并联跟踪机构的承载能力。多个3-RPS并联跟踪机构相互独立，协同控制使得聚光器保持抛物面不变。

图3 RPS支链结构爆炸图Fig.3 Exploded view of RPS branch chain structure

2 位置逆解与雅可比矩阵

2.1 机构位置逆解

经典3-RPS并联机构的构型为动、定平台为等边三角形且转动副轴线共面并平行于三角形对边[19-20]，对于新型碟式太阳能聚光器，由于聚光器镜面单元的排布设计，动平台安装于镜面单元相切的基准平面上，在单块镜面单元尺寸确定的情况下，动平台形状应与单块镜面单元在安装平面的投影相近，基于此，3-RPS并联跟踪机构的动、定平台为等腰三角形为宜，下文建立通用3-RPS 并联机构的位置逆解方程。

在通用3-RPS并联机构中，动、定平台为任意三角形，且转动副轴线垂直于定平台中心与顶点的连线。图4为通用3-RPS并联机构的结构简图，设动平台球副中心点为Si，定平台转动副中心点为Bi，令动、定平台的外接圆半径分别为R、r，以动平台中心C为原点建立动坐标系CX1Y1Z1，Z1轴垂直于动平台竖直向上，X1轴正向沿直线CS1指向S1，Y1轴由右手定则确定。同样以定平台中心O为原点建立定坐标系OX2Y2Z2，Z2轴竖直向上，X2轴正向沿直线OB1指向B1，Y2轴由右手定则确定。

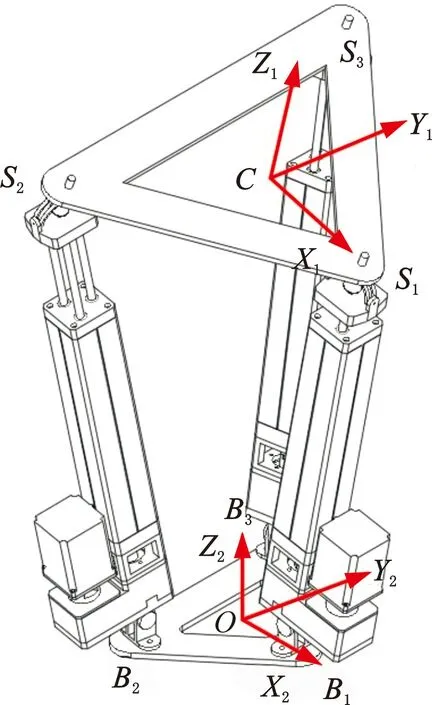
图4 通用3-RPS并联机构的结构简图Fig.4 Kinematic diagram of general 3-RPS parallel mechanism

用向量矩阵PCS和POB表示出CSi和OBi，即：

(1)

(2)

式中，cφ表示cosφ，sφ表示sinφ，下文出现的正弦和余弦函数都作类似简化；φ为向量OB1与OB2、向量CS1与CS2之间的夹角；φ为向量OB1与OB3、向量CS1与CS3之间的夹角，逆时针方向为正；R为动平台半径；r为定平台半径。

通用3-RPS并联机构的动平台具有沿Z1轴方向的移动自由度和绕X1、Y1轴的两个偏转自由度，为便于分析动平台的偏转能力，采用Z-Y-X型欧拉角(γ，β，α)描述动平台姿态，则其姿态矩阵为

(3)

动平台球副中心Si在定坐标系可表示为

(4)

式中，(xC，yC，zC)T为点C在定坐标系的坐标。

根据通用3-RPS并联机构支链向量Li恒垂直于转动副的轴线向量的几何约束关系，则有

Li·ei=0

(5)

式中，ei=(μi，νi，0)T为转动副轴线的单位方向向量。

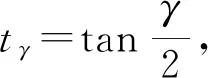
(6)

综合式(5)和式(6)可求出动平台的位姿参数(xC，yC，γ)关于机构尺寸参数的位姿耦合关系式：

(7)

式中，h1、h2、h3为关于动平台位姿参数(α，β)和机构结构尺寸参数的函数式。

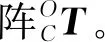
根据闭环矢量三角形和定杆长方程可得通用3-RPS并联机构位置逆解方程：

Li=‖OSi-OBi‖=‖SiBi‖

(8)

2.2 位置逆解验证

为验证通用3-RPS并联机构位置逆解的正确性，本文采用MATLAB软件进行理论计算，并借助ADAMS软件进行运动仿真验证。将简化后的机构虚拟样机模型导入ADAMS软件，并对机构的运动副和驱动进行定义，建立其运动仿真模型，如图5所示，设置动平台的运动规律为

(9)

图5 通用3-RPS并联机构ADAMS运动仿真模型Fig.5 ADAMS motion simulation model of general 3-RPS parallel mechanism

MATLAB计算的位置逆解结果与ADAMS的仿真结果对比如图6所示。对比可知，数值计算结果与仿真结果稍有误差但基本一致，误差主要来自于ADAMS的测量误差，由此验证了位置逆解的正确性。

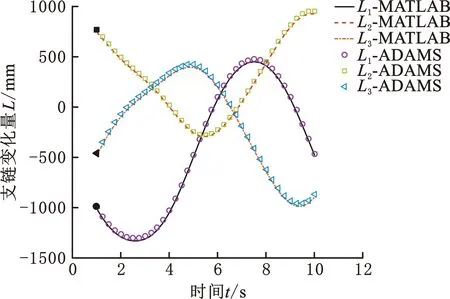
图6 MATLAB和ADAMS位置逆解结果对比Fig.6 Comparison of MATLAB and ADAMS position inverse simulation results

2.3 雅可比矩阵求解

动平台上各球副中心点Si的速度矢量可表示为

vsi=v+ω×Ri

(10)

式中，v为动平台C点的速度，v=(vx，vy，vz)T；ω为动平台的角速度；Ri为点C指向点Si的位置向量。

RPS支链的移动副的线速度vli可表示为速度矢量vsi在支链方向li的投影，即

(11)

i=1，2，3

式中，li为RPS支链始端指向末端的单位方向向量，li=Li/‖Li‖。

式(11)写成矩阵形式：

(12)

式中，Jma为机构的驱动雅可比矩阵。

根据螺旋理论，结合图4可知，通用3-RPS并联机构各运动关节的运动螺旋为

(13)

式中，Sj，i为第i条RPS支链上的第j个运动关节的轴线单位矢量；S为螺旋轴线的单位方向矢量；bi为点O指向点Bi的位置向量；ei为转动副轴线的单位方向向量。

由螺旋理论可知，运动螺旋与约束螺旋互易积为零，其中约束螺旋为

(14)

动平台中心C的速度可以表示为

SC=[v；ω]T

(15)

将式(14)与式(15)两边作互易求积，可得

(16)

写成矩阵形式：

(17)

式中，Jmb为机构的约束雅可比矩阵。

综合式(12)和式(17)可得

(18)

3 机构性能评价指标

3.1 灵巧度

雅可比矩阵的条件数K(J)是定量描述机构输入和输出之间的运动/力传递精度的重要指标，通常采用雅可比矩阵条件数的倒数来表示并联机构动平台在特定位姿下的局部灵巧度[15]，即

(19)

其中，K(J)=cond(J)=‖J‖‖J-1‖。局部灵巧度的取值范围为[0，1]，且雅可比矩阵的条件数越小，机构的灵巧度越大，机构运动/力传递性能越好。由于LCI只能评价机构在特定位姿下的灵巧度，故引入全域灵巧度指标GCI用以评价机构在工作空间全域下的运动/力传递性能，表达式为

(20)

式中，w为机构的可达工作空间。

3.2 刚度指标

机构的刚度是指动平台在外力/外力矩的作用下，由于部件的弹性变形所引起的位移的大小，它随着动平台位姿的变化而变化[21]。机构的系统刚度写成矩阵表达式为

F=KmΔε

(21)

Km=JTknJ

(22)

kn=diag(k1，k2，k3)

式中，F为作用在动平台的广义外力；Δε为在F作用下产生的形变；Km为并联机构的刚度矩阵；kn为驱动副的关节刚度。

由于刚度矩阵Km是并联机构刚度的张量测度，因而用来衡量机构的刚度性能不直观。为了得到衡量刚度的标量测度，引入刚度矩阵的瑞利商S来评价机构的刚度大小[22-23]：

(23)

(24)

3.3 承载能力指标

(25)

联立式(18)与式(25)可得

N=Jdf

(26)

式中，Jd=JT，Jd为力雅可比矩阵。

承载能力指标定义为当输入力矢量f的模为1时，输出力/外力矩矢量N极值的大小[24]，为求得N的极值大小，构造拉格朗日目标方程：

(27)

式中，κ为拉格朗日乘子。

式(27)求导得极值条件：

(28)

由式(28)可得动平台输出的力/力矩N的极值：

(29)

选取机构的最小承载能力极值‖Nmin‖作为机构在特定位姿下的承载能力指标，‖Nmin‖越大，机构的承载能力越好。同样地，引入全域承载能力性能指标GL对机构在可达工作空间内的全域承载能力性能进行评价，其计算式如下：

(30)

4 机构参数优化

新型碟式太阳能聚光器在单块聚光器镜面单元尺寸确定的情况下，其安装镜面单元的3-RPS并联跟踪机构的结构参数对跟踪平台的工作性能有重要影响。上文建立了多个并联机构性能指标，本文所设计的新型碟式太阳能聚光器在拥有良好的灵巧度的同时也应具备良好的刚度和承载能力，为此采用多目标遗传算法进行结构参数优化。

4.1 优化变量

由前文可知，新型碟式太阳能聚光器的主要结构参数有R、r、α、β。由于动平台作为安装聚光器镜面单元的背板，安装在相切于碟式聚光镜的基准平面上，在单块聚光器镜面单元的尺寸确定的情况下，动平台半径R和结构参数α、β是给定的，因此不作为优化变量。选用定平台半径r作为优化变量，r的优化范围为

600 mm≤r≤1000 mm

4.2 优化目标

新型碟式太阳能聚光器的原型机构为通用3-RPS并联机构，其结构参数设计为单变量。多目标优化设计，最终确定的结构参数无法使3个性能指标均达到最优，只能结合机构的结构布局、构件协调关系、实际需求等综合选取各性能指标的较优值。多目标优化的策略方法有线性加权法、最小二乘法等，本文采用线性加权法重新构造新的优化目标函数将多目标优化问题转变为单目标优化问题，基于式(20)、式(24)以及式(30)的性能评价指标建立优化目标函数：

maxΦ(x)=w1GCI+w2GS+w3GL

(31)

式中，w1、w2、w3为各性能指标的权重系数，w1+w2+w3=1。

对于新型碟式太阳能聚光器，由于聚光器镜面单元作为3-RPS并联跟踪机构安装的末端执行器，其动平台安装于镜面单元的相切基准平面上，3-RPS并联跟踪机构的灵巧度关系着镜面单元的控制精度，从而影响新型碟式太阳能聚光器的跟踪精度，因此在新型碟式太阳能聚光器的优化设计中，机构的灵巧度作为主要的优化目标。根据新型碟式太阳能聚光器的灵巧度、刚度、承载能力的实际需求，最终综合考虑各性能指标，设各目标加权系数分别为：w1=0.4，w2=0.3，w3=0.3。

4.3 约束条件

新型碟式太阳能聚光器的运动主要受支链运动行程、转动副转角范围以及球副转角范围的约束，即

(32)

式中，Lmin、Lmax分别为支链的最小和最大极限长度，Lmax=2Lmin，支链的最小极限长度为2000 mm；ζRmax为转动副的最大转角，为120°；ζSmax为球副的最大转角。

合理选择球副能够使新型碟式太阳能聚光器获得更大的工作空间，文献[25]提出了一种大工作空间的新型被动球铰链，本文加以改良作为RPS支链的球铰链，如图7所示，其输出杆的极限位置如图8所示。由于双耳支架的干涉限制，新型被动球铰链输出杆的摆动空间为以球头中心为圆心的圆锥体，故根据几何关系得到新型被动球铰的最大转角

(33)

式中，H为双耳支架的销孔中心到双耳支架上表面的距离；Ru为U型拨叉的半径；Rp为输出杆的半径。

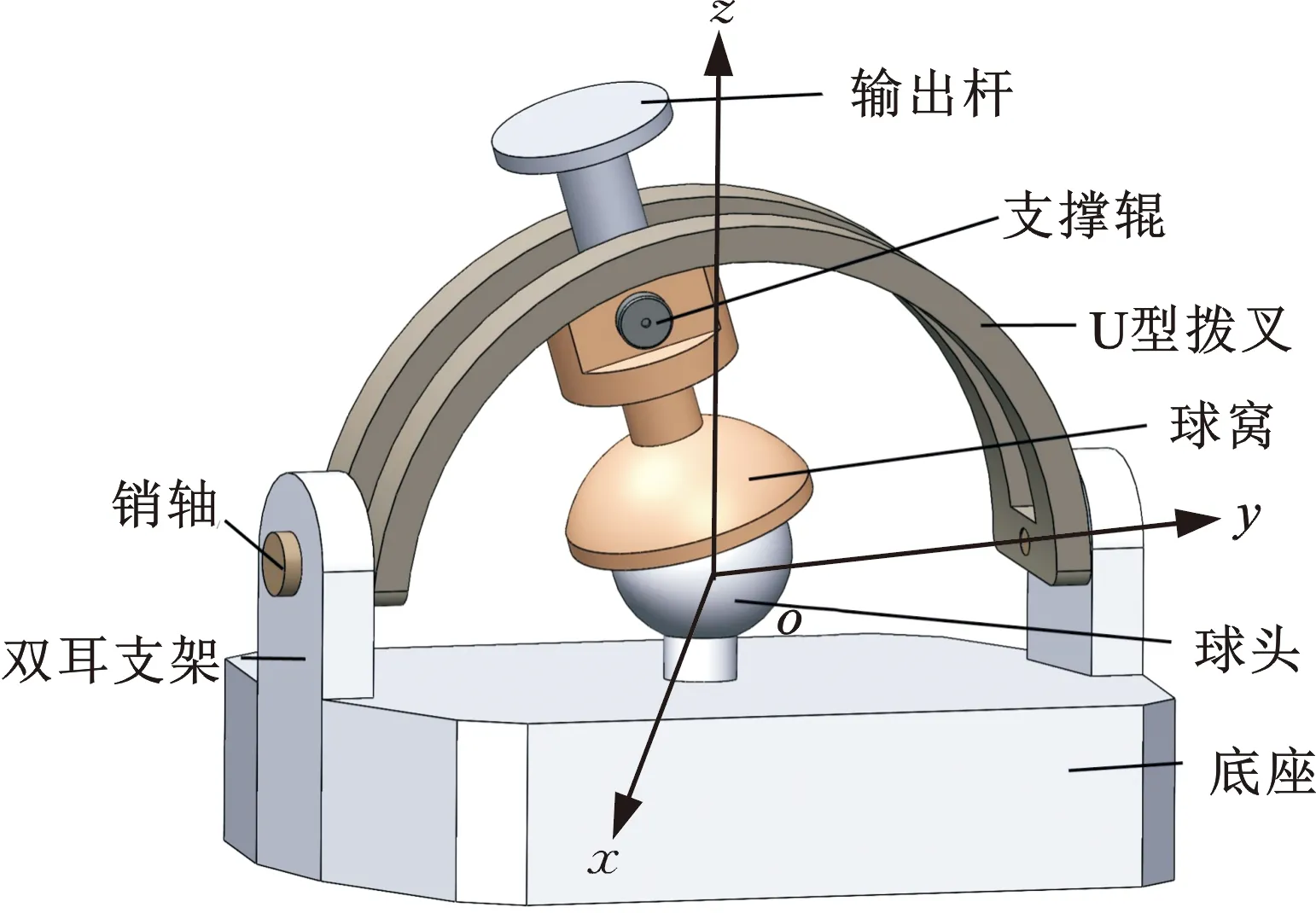
图7 新型被动球铰链Fig.7 New passive spherical hinge

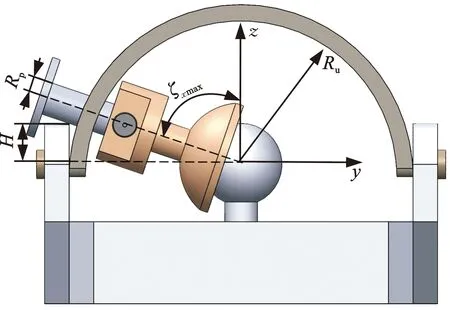
图8 新型被动球铰链的极限位置Fig.8 Limit position of the new passive spherical hinge

本文中新型被动球铰的结构参数为：H=70 mm、Rp=35 mm、Ru=200 mm，求得最大转角经圆整后为60°。

4.4 优化模型求解

基于多目标遗传算法对新型碟式太阳能聚光器的结构参数进行优化，其中遗传算法的运行参数设置为：动平台半径R=1425 mm，α=100°，β=260°，种群中的个体数目M=100，最大迭代次数Q=100，变量二进制位数E=20，代沟T=0.9，变异概率Pm=0.2，交叉概率Px=0.8。

运算过程中，首先优化模型通过随机抽样法选择初始个体种群，然后,对每一个个体进行函数Φ(x)的求解，步骤如下：

(1)判断优化模型产生的个体r1，r2，…，rn是否满足约束条件。若不满足，则是不可行解，此时F(x)=0，并结束此个体种群在程序中的计算，并进行下一个体代表的种群数据的计算。

(2)在计算函数Φ(x)时，需要计算机构的可达工作空间。首先根据球坐标搜索法，判断3-RPS并联机构动平台中心点C在给定位姿处对应的各运动副(移动副、转动副以及球副)是否在运动范围内，若在运动范围内，则动平台在可达工作空间内，然后计算给定位姿处的Φ(x)值。

(3)重复步骤(2)直到完成整个可达工作空间的搜索，搜索出满足约束条件的点的集合w，进一步计算函数Φ(x)的值。

(4)终止约束条件的判断。对一代个体的函数F(x)值计算完毕后进行终止判断，若满足要求，则终止运算，得到较优解；若未找到优化模型的较优解，则继续进行下一步计算。

(5)重复步骤(2)、(3)的运算，对个体进行交叉、变异获得下一代个体种群。

机构参数优化迭代过程中目标函数值Φ(x)的变化情况及迭代代数为100时各种群个体对应的目标函数值Φ(x)分别如图9和图10所示。

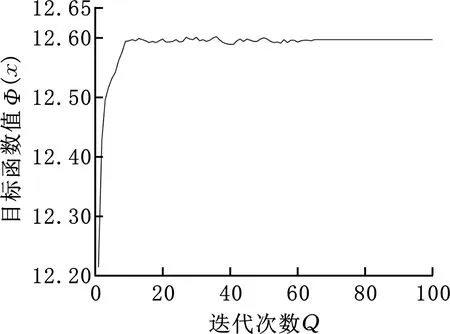
图9 迭代过程中目标函数值的变化情况Fig.9 Variation of the objective function value during the iteration

图10 迭代次数为100时各种群个体对应的目标函数值Fig.10 Objective function corresponding to each groups of individuals with 100 iterations

由图9可知，当迭代次数达到12时，目标函数值在12.58附近波动，说明此遗传算法迭代至第12代时即可达到收敛，此时对应的定平台半径r为新型碟式太阳能聚光器的定平台最优参数。由图10可知，当迭代次数为100时，仅2个种群个体偏离目标函数值较远，其余的种群个体均在可接受的范围内，此现象说明此遗传算法的精度较高。

4.5 优化结果分析

新型碟式太阳能聚光器经过遗传算法优化后，得到优化后的定平台半径大小，通过圆整处理后，取定平台半径r=860 mm。优化前后新型碟式太阳能跟踪装置的尺寸参数及各性能指标对比如表1所示，通过比较可以得出优化后新型碟式太阳能聚光器的全域灵巧度提高了24.9%，全域刚能性能指标提高了16.7%，全域承载能力指标提高了25.2%。

表1 优化前后各性能指标对比

基于优化前后的定平台半径的尺寸参数，当动平台处于安装高度ZC=(Lmax+Lmin)/2即ZC=3000 mm时，优化前后各性能指标分布对比如图11～图13所示，可以看出优化前后机构各性能指标明显得到提高。

(a)优化前LCI性能图谱 (b)优化后LCI性能图谱图11 优化前后LCI性能分布对比Fig.11 Comparison of LCIperformance distribution before and after optimization

(a)优化前S性能图谱 (b)优化后S性能图谱图12 优化前后S性能分布对比Fig.12 Comparison of S performance distribution before and after optimization

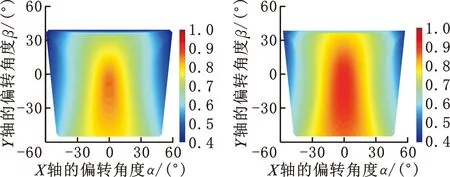
(e)优化前‖Nmin‖性能图谱 (f)优化后‖Nmin‖性能图谱图13 优化前后‖Nmin‖性能分布对比Fig.13 Comparison of‖Nmin‖performance distribution before and after optimization

5 ANSYS有限元仿真验证

为验证机构参数优化的正确性，本文采用ANSYS Workbench软件建立机构参数优化前后的新型碟式太阳能聚光器受到相同外力/外力矩时的静应力分析模型，得到动平台处于相同位姿下的变形量与应力云图，如图13所示。

根据图14分析得出，优化前后的3-RPS并联跟踪机构在受到相同外力/外力矩作用时，优化前机构的最大变形量为0.358 mm，最大应力为120.17 MPa，优化后机构的最大变形量为0.235 mm，最大应力为98.929 MPa。优化后的机构的刚度和承载能力明显高于优化前，因此优化后的3-RPS并联跟踪机构的刚度和承载能力得到了提高，验证了本文机构参数优化的正确性。