改进烟花算法计算热态轴类锻件内圆柱体空洞缺陷深度

沈久利 张玉存

燕山大学电气工程学院，秦皇岛，066004

0 引言

大型轴类锻件被广泛应用在石油、能源、电力、航空航天、船舶等领域。生产大型轴类锻件过程中，若在锻件处于锻造完成后的冷却降温时段检测出内部含有缺陷，则需要重新回炉加热和再锻造，会造成资源的极大浪费。若在生产中不能及时发现锻件存在问题的相关性能指标，其使用寿命会受到影响[1]。与表面缺陷相比，锻件内部缺陷的破坏更为严重[2]，因此，及时、准确地检测出内部缺陷，对大型锻件的制造与生产具有非同寻常的意义。目前，锻件内部缺陷的检测方法主要有射线检测、超声检测、红外检测等[3-6]。红外无损检测技术具有抗干扰性强、非接触、一次观测面积较大等特点，适用于外场在线在役检测以及监测一类疲劳腐蚀损伤的发展性缺陷[7-8]。VALENCIA等[9]利用红外检测对气缸盖等平面进行缺陷分析，证明红外检测技术对气缸盖缺陷检测的可靠性更高。KALHOR等[10]利用红外热成像检测涵洞周围土壤中的空洞和镀锌涵洞管道附近的空洞，通过分析热图提取出空腔大小和位置信息。MARANI等[11]将阶跃加热红外热像技术和深层神经网络算法相结合，提出了复合材料层合板缺陷深度的自动检测方法。刘涛等[12]利用脉冲红外热成像检测法实现了铝蜂窝板缺陷的检测。习小文等[13]、王博正等[14]、杜金尧等[15]通过超声红外热成像技术检测产生裂纹的航空发动机叶片试件，能准确检测出试件的裂纹缺陷。虽然以上研究利用红外技术检测出了内部缺陷，但未能检测出缺陷的位置、尺寸等信息。

对于热态轴类锻件空洞缺陷深度的计算，由于瞬态温度场模型与缺陷深度相关函数较多且求解复杂，利用数值解方法求解时，影响缺陷深度计算精度的重要因素是最优算法，故本文引入烟花算法对缺陷深度进行定量检测，构建热态轴类锻件内部圆柱体空洞尺寸检测模型，利用分离变量法求解圆柱体空洞缺陷温度场及尺寸之间的微分方程。在此基础上对传统烟花算法的爆炸算子、变异算子和选择策略分别进行改进，利用改进的烟花算法计算空洞缺陷深度，将缺陷深度求解问题转换为计算空洞缺陷深度的目标函数求最优解问题，提高空洞深度检测精度与速度。通过对标准函数和构造的目标函数进行仿真实验和空洞缺陷深度测量实验，验证所提方法的可行性。

1 圆柱体空洞缺陷半径模型及求解

1.1 圆柱体空洞缺陷半径模型

如果将大型轴类锻件看作宏观尺寸，那么空洞的尺寸就需要看作无限小，空洞所在的局部空间就应该看作一个微元。

由直角坐标系转化为柱坐标系公式可知[16]：

(1)

将式(1)对x、y分别求偏微分∂R/∂x、∂φ/∂x、∂R/∂y、∂φ/∂y，由复合函数求导规则可得∂T/∂x和∂T/∂y；再分别对T、x、y求导，计算得到柱坐标系下的导热微分方程：

(2)

式中，R为轴类锻件的半径，m；φ为极角，rad；扩散系数α=μ/(ρc)，m2/s；μ为微元体材料的热导率,W/(m·K)；ρ为被测物体密度，kg/m3；c为被测物体质量热容，J/(kg·K)；K为圆柱形空洞体单位时间单位体积内生成的热量，J。

当轴类锻件内无内热源时K=0，其非稳态的热传导微分方程可描述为

(3)

式(3)即为圆柱坐标系下的轴类锻件在非稳态时的温度场传热微分方程。

热态锻件含圆柱形空洞的轴类锻件示意图见图1。设圆柱形空洞的半径为R1，高度为z，空洞的温度为T1。

图1 含圆柱形空洞的轴类锻件示意图Fig.1 Diagram of shaft forgings with the solidcylinder pore

根据式(3)可分别得到空洞处的温度场微分方程和轴类锻件处温度场微分方程：

(4)

(5)

其中，α1为柱形空洞的热扩散系数，m2/s；α2为轴类锻件不含空洞处热扩散系数，m2/s；τ为冷却时间，s。锻件的半径为R2，高度为d2，锻件的温度为T2。

1.2 基于分离变量法的圆柱体空洞缺陷半径求解

轴类锻件温度梯度以径向为主且锻件未达到稳态，锻件处温度场方程式(4)可简化为

(6)

偏微分方程式(5)包含两个自变量且微分方程及边界条件为齐次方程，符合分离变量法的条件，采用分离变量法对其求解。将式(5)分解成关于Tq(R)的稳态问题和关于TV(R,τ)的齐次问题。稳态方程为

(7)

其中，h1为圆柱形空洞和轴类锻件间的复合传热系数，W/(m2·K)；h2为周围空气和存在空洞缺陷的轴类锻件外壁之间复合换热系数，W/(m2·K)；Τa为周围大气温度，℃。

齐次方程为

(8)

求解式(5)、式(7)组成的稳态方程可得

Tq(R)=c1+c2ln(R)

(9)

其中，c1、c2是根据稳态方程定解条件计算得到的常数项。对分离后的齐次方程式(7)求解可得

(10)

由线性叠加原理和初始条件，结合式(7)的正交性得到齐次方程的解：

(11)

其中，Ψ(R)为空间函数。

将问题方程的解和齐次方程的解进行叠加，可得圆柱形空洞处温度场方程的解：

(12)

同理，热态轴类锻件处温度场方程的解是

(13)

式(12)和式(13)为锻件及圆柱形空洞缺陷处的温度场与空洞半径、时间、扩散、传热系数及热导率之间模型的解。至此，采用分离变量法求出了圆柱体空洞处的温度场与空洞半径、时间、扩散系数、传热系数、热导率之间方程的解。

2 改进烟花算法的圆柱形空洞深度检测

2010年，谭营[17]提出了一种群体智能算法——烟花算法(fireworks algorithm，FWA)。烟花的爆炸半径决定爆炸火花的位置，影响种群的多样性；变异算子利用模运算映射，该算法复杂、计算量较大、效率低；运用模运算的映射规则来处理火花粒子的超界问题，算法的收敛速度会变快，但种群的多样性会降低，且最优值不在零点时寻优效果并没有优势。由于忽略了基于距离的选择策略，烟花种群的多样性不能得到保证，易陷入局部最优解，不利于圆柱体空洞深度的检测。

2.1 构造热态锻件圆柱形缺陷深度目标函数

当轴类锻件空洞缺陷中心处对应的轴类锻件外表面温度与空洞缺陷中心处温度的差值最大时，可得到空洞缺陷的深度。圆柱体空洞缺陷如图2所示，其中，D为空洞缺陷深度，R1为空洞半径，R2为锻件半径。

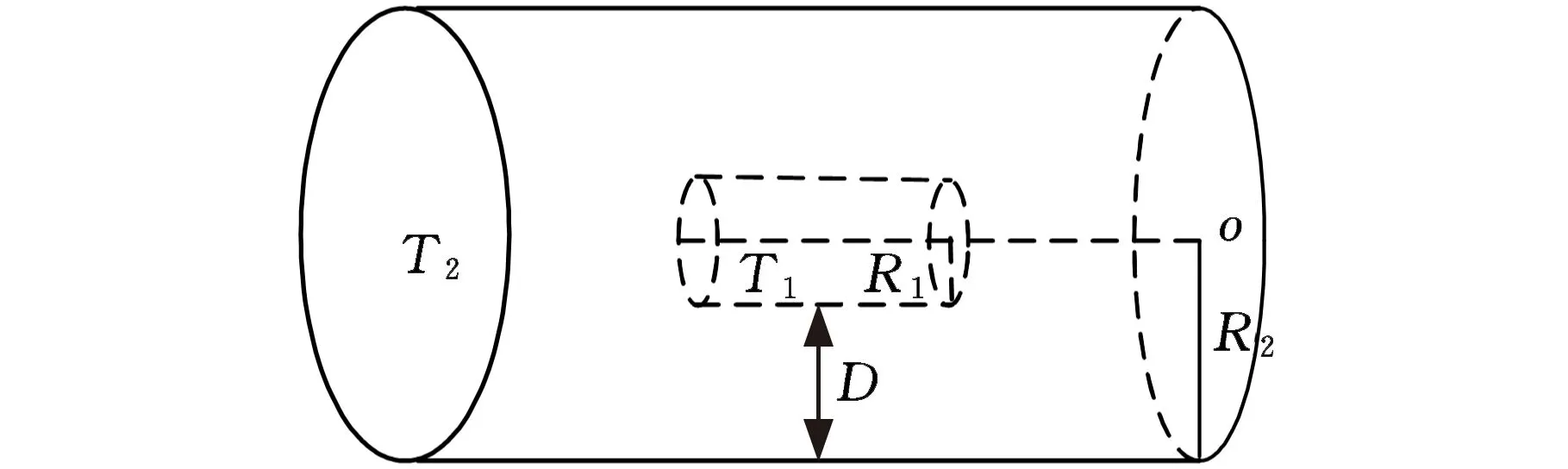
图2 空洞缺陷深度示意图Fig.2 Diagram of pore defect depth

利用FWA算法得到缺陷深度的最优值即可计算空洞缺陷深度。根据式(12)和式(13)，定义FWA的目标函数为

P(D)=|Tt(D+R1)-T(t)|

(14)

其中，Tt(D+R1)为t时刻空洞缺陷中心处的温度；T(t)为轴类锻件在t时刻空洞缺陷中心处对应的轴类锻件外表面的实际温度值，即红外测温系统测得温度值。

圆柱形空洞缺陷深度的目标函数可表示为

(15)

求式(15)最大值，适应度高的种群个体对应目标函数值越大可行性越高。适应度函数为

Fitnessi=1/Eii=1,2,…,K

(16)

其中，Fitnessi是第Ei个个体的适应度；Ei是第dm=maxx∈ΩFitness(x)个个体对应的目标函数值；K为群体的规模。

目标函数在可行解空间的最优解为

dm=maxx∈ΩFitness(x)

(17)

其中，Ω是x的可行解空间。

由于空洞的体积非常小，要精准确定空洞的深度，需要提高FWA的精度。同时，热态轴类锻件处于非稳态，温度随着时间实时变化，所以要求寻优算法快。而现有FWA耗时严重，会严重降低检测的精准度，因此基于算法的不足以及在计算空洞缺陷深度时的实际需求对FWA进行改进。

2.2 改进的FWA

针对传统FWA存在的缺点，分别就爆炸算子、变异算子、选择策略三方面提出改进方法。

(1)爆炸算子改进。针对传统的算法容易使寻优结果陷入局部最优值的问题，引入混沌搜索的Cubic映射算法，它具有随机性、规律性及遍历性，可避免搜索过程陷入局部最优值。

Cubic映射算法产生爆炸半径为

Cn=r(Cn-1)3-(1-r)Cn-1

(18)

式中，r为爆炸半径；Cn为混沌域，Cn∈(-1,1)，n=0,1,…。

则Cubic混沌方法产生爆炸半径为

(19)

式中，R(i)t为当代第i个烟花的爆炸半径；R(i)t-1为上一代与之对应的烟花个体爆炸半径；R(i)t-1为边界值为[-1,1]的混沌域。初始烟花半径可以在混沌域内任意选择。

为了改善算法中个体的爆炸数目与半径，借助转移函数：

Ta′(n)=1/(1+exp((n-1)/a′))

(20)

其中，a′是一个改变转移函数形状的参数，n是烟花序号。烟花的爆炸半径和爆炸的火花数量会根据适应度进行调整，可提高算法收敛速度。

则改进后烟花爆炸数量为

(21)

式中，m为烟花爆炸的数目之和；Sn为第n个烟花爆炸产生的火花数；N为烟花的数目；Ta′(n)中的参数a′随着算法迭代从20逐步减少到1。

对烟花爆炸幅度改进后，得

(22)

其中，A是烟花爆炸最大的幅度，An是第n个烟花爆炸的幅度。为了降低烟花个体很接近最优解(即烟花的爆炸半径几乎为0)时新解产生的难度，避免陷入局部收敛，加入了最小爆炸半径的检测机制，即

(23)

其中，Aik是在维度k上烟花i的爆炸半径，Amin,k是在第k维上的爆炸半径最低的检测阈值。采取线性递减爆炸半径检测策略或非线性递减爆炸半径检测策略，则Amin,k可分别表示为

Amin,k(k)=Ainit-(Ainit-Afinal)/emax

(24)

(25)

式中，Ainit为爆炸半径的初始值；Afinal为爆炸半径的终止值；emax为最大评估数；k为当前迭代的评估次数。

(2)变异算子改进。针对映射规则没有考虑爆炸生成火花边界范围的问题，对变异算子进行改进。随机映射能够有效减少计算量，避免超出边界的火花总是被映射到远点附近，对位移函数的优化能力有所提高，且在处理高维问题时能够提高计算效率和确保数据独立性，有利于实现温度不断变化的热态轴类锻件内部空洞深度的精准检测。随机映射为

(26)

(3)选择策略的改进。针对传统精英策略的问题引入精英候选集策略，该策略一是选择爆炸火花的定向机制，二是选择变异火花的“优胜劣汰”机制。

①定向机制。首先筛选每个烟花爆炸产生的火花，适应度相对较差的火花有较低机率被选进候选集，而适应度相对较好的火花则有较高的机率被选进候选集。通过下式确定火花被加入候选集的概率：

(27)

式中，fmin、fmax分别为当前烟花爆炸产生火花适应度的最小值和最大值。

精英候选集策略的下一代火花只会在当代烟花爆炸半径范围内适应度值比较优的位置产生，既剔除了无益于算法局部寻优的劣质火花，提升候选集中烟花的质量，又减少了候选集中相同烟花爆炸产生的火花数量，提高了下一代种群的多样性。

②“优胜劣汰”机制。精英候选集策略筛选变异个体，选入适应度较好的火花，淘汰适应度较差的火花。变异火花被选中候选集的概率也通过式(27)来确定，此策略保证了候选集的质量，并且对同烟花的火花过多地被选择为下代种群的概率有降低效果，提高了寻优效果，利于提高轴类锻件内部空洞缺陷深度的计算。

2.3 空洞缺陷深度检测流程

改进的FWA计算锻件内部空洞深度的步骤如下：

(1)构造适应度函数，根据实际参数对烟花种群初始化设置参数；

(2)根据式(19)计算烟花的爆炸半径，并利用式(25)来控制爆炸半径，计算各烟花适应度；

(3)计算爆炸后火花产生位置，利用精英候选集策略选取适应度好的爆炸火花，形成高斯火花；

(4)利用式(26)将可行解空间以外的火花映射到可行解空间范围内；

(5)计算随机抽取的两个独立个体之间的距离，根据式(27)计算每一个个体被选为下一代烟花的概率；

(6)根据精英候选集策略选择下一代烟花群体，转至步骤(2)；

(7)计算每个个体的适应度，目标函数是求最小值，适应度越小的个体解越优，根据适应度值不断更新个体的最优位置；

(8)判断是否满足迭代结束条件，若满足则迭代结束，将全局最优解的位置输出，得到寻优结果；否则继续重复步骤(2)～(5)；

(9)输出空洞缺陷深度。

3 实验

3.1 实验设备

本文涉及的实验设备有热电偶、实验锻件、旋转装置、加热系统、红外热像仪等。热电偶为铂铑热电偶(型号为WRP-130)，测温范围为0～1600 ℃，最大误差为±1.5 ℃。加热系统由箱式电阻加热炉(型号为SRJX-8-13)和温度控制器(型号为SKY-12-16)组成。采集轴类锻件红外图像的红外热像仪的型号为VarioCAM hr research 680。实验锻件之一如图3所示，参数见表1，限于篇幅，只列出温度为800 ℃时的质量热容。

图3 实验锻件Fig.3 The experimental forging

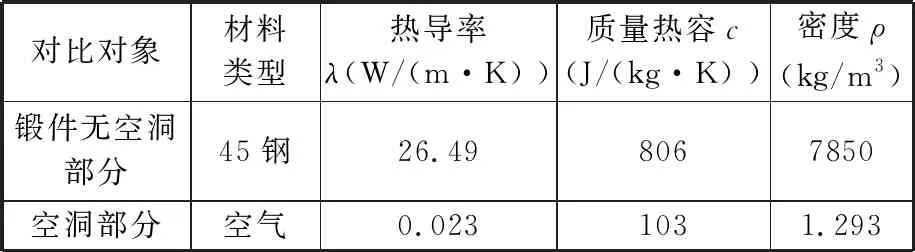
表1 实验材料热物理参数

3.2 标准函数仿真实验

为了验证改进的FWA算法计算空洞缺陷深度的可操作性，将标准函数与锻件内部含有圆柱形空洞缺陷时构建的目标函数作为验证的对象。

(1)标准函数寻优。通过14个标准函数来测试改进的烟花算法的有效性和可行性。f1～f14标准函数如下：f1～f5为单峰函数，f6～f10为多峰函数，f11～f14为旋转函数，各函数的搜索范围为[-100,100]。采用粒子群算法(PSO)、FWA与改进的FWA算法进行对比。设置参数见表2，PSO算法的种群规模设置为50，维度为30，运行50次，停止的标准为最大函数评估数。14个测试函数的最优适应度与标准差在三种算法下的结果见表3。

表3中，改进的FWA与FWA对比后可知，对于f1～f6、f8、f10～f14，改进的FWA求出的最优适应度、标准差这两个测试指标最好；改进的FWA与PSO算法对比后可知，对于f1～f6、f8～f11、f13、f14，改进的FWA求出的最优适应度、标准差这两个测试指标最好；对于函数f7，PSO算法的适应度和标准差都是最优，改进的FWA虽然不是最优，但与PSO算法求出的适应度与标准差相差不多；对于函数f9，FWA的适应度与标准差是最优的，改进的FWA虽然不及FWA，但比PSO算法的寻优结果好。

综上，改进的FWA的适应度和标准差这两项测试指标的结果相比FWA和PSO有明显优势，验证了改进的FWA的有效性及可行性。

(2)目标函数寻优。以圆柱形空洞缺陷温度场与空洞半径尺寸的微分方程的结果作为实际测量温度值，使用改进的FWA对缺陷深度为2 mm、时间为0.8 s的微分方程求解出的温度值进行寻优，参数见表2；对计算得到的温度值进行寻优，收敛曲线如图4所示。

由图4可知，算法在第12次迭代时第一次陷入局部最优解，但随着变异火花的爆炸以及迭代次数的增加，不断向最优解逼近直至最终输出最优解，缺陷深度为1.9506 mm，相对误差为2.5%，证明了本文算法的可行性。

3.3 圆柱形空洞深度测量实验

(1)同一深度空洞的实验。为了验证改进的FWA算法的可行性和精确性，将空洞的深度设置为3 mm，空洞的半径设为2.5 mm，空洞的长度设为10 mm，其他参数与表1和表3相同。采集900 s、1200 s、1500 s、1800 s、2100 s时锻件中心处温度值与空洞中心处值，构造目标函数，用FWA、改进的FWA和PSO分别进行空洞深度寻优，收敛曲线如图5～图7所示。

表3 三种寻优结果对比

图4 烟花算法收敛曲线Fig.4 The convergence curve of FWA

图5 FWA收敛曲线Fig.5 The convergence curve of FWA

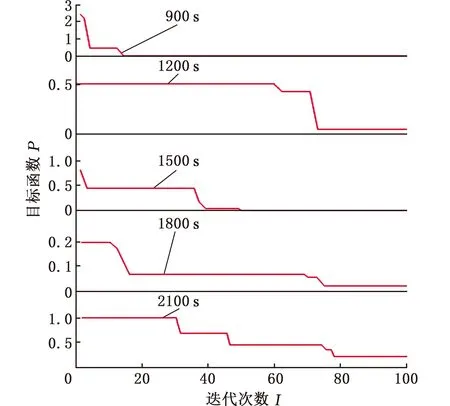
图6 改进的FWA收敛曲线Fig.6 The convergence curve of the improved FWA

图7 PSO收敛曲线Fig.7 The convergence curve of PSO

经典PSO算法在定量计算空洞深度时收敛速度比烟花算法要快，收敛后的适应度波动较小，但缺点是容易陷入局部最优解。FWA算法简单，容易陷入局部最优且精度差。改进的FWA算法后，每次爆炸都有新的火花产生和一部分变异火花的择优选取，使改进的FWA算法在定量计算空洞深度时的全局搜索能力更强，适应度值更大，寻优结果更接近真实值。由表4可知，改进的FWA算法计算误差在2.5%以内，比PSO算法和FWA算法的误差小，证明了改进的FWA在定量计算空洞深度时的有效性，同时具有稳定性高且适应度好的特点。

表4 PSO、FWA和改进的FWA的寻优结果比较

(2)不同深度空洞的实验。本组实验的空洞深度分别设置为1 mm、3 mm、5 mm、7 mm、9 mm、12 mm，空洞的半径设为2.5 mm，空洞的长度设为10 mm，其他参数和表1、表2相同。对900 s、1800 s、2400 s和3600 s时刻锻件中心处温度值与空洞中心处温度值构造目标函数，利用改进的FWA进行空洞深度寻优，结果见表5。

由表5可知，对于不同深度的空洞，改进的FWA的寻优效果不同，同一时刻空洞深度越小，寻优效果越好误差值越小，说明离锻件表面越近的空洞越容易被检测。随着空洞深度的不断增加，寻优精度变差，但测量误差均在5%以内，说明对于较深的空洞，本文检测方法仍然适用。同一空洞深度下检测误差随着时间的推移先变小后

表5 不同空洞深度下改进的FWA的寻优结果

变大，说明锻件中心处与空洞中心处的温度差先变大后变小，且时间对检测误差的影响比空洞深度的增加对误差的影响更明显。

4 结论

(1)本文利用微元模型得到圆柱体缺陷温度的检测模型，通过分离变量法得到方程的解析解，实现了利用温度场对热态轴类锻件内部圆柱体空洞半径的信息进行检测。

(2)构造了轴类锻件外表面温度与圆柱体空洞缺陷中心处温度的差值最小的目标函数，运用改进的烟花算法计算空洞缺陷深度。改进后的烟花算法每次“爆炸”都会产生新的“火花”，还会随机生成“变异火花”，不易陷入局部最优解，全局搜索能力得到改善，对空洞的深度进行计算，计算误差为2.5%，为热态轴类锻件内部规则缺陷深度检测提供了新的思路。

(3)进行了圆柱形空洞深度测量实验，分别用PSO、FWA和改进的FWA算法对同一深度空洞缺陷进行了检测，实验结果表明改进的FWA算法的计算误差为2.5%以内。运用改进的FWA算法对不同深度的空洞进行了检测，实验结果表明计算误差均在5.0%以内。