基于交叉小波变换与改进变分模态分解的联合去噪方法*

王鹏博,刘自然,刘玉明,吕振礼

(河南工业大学 机电工程学院,河南 郑州 450001)

0 引 言

机械设备在长期的运转过程中容易出现故障,导致设备停转,甚至造成重大的经济损失,因此,提前对机械设备进行故障检测是非常有必要的[1]。滚动轴承作为旋转机械的重要部件,也是易出现故障的结构,因此,对其故障进行诊断具有重要的意义[2]。

由于滚动轴承早期的故障信号微弱,极易被淹没在噪声之中,呈现非平稳、非线性等特点,导致滚动轴承故障特征难以被提取,增加了其故障诊断的难度[3]。

国内外学者对旋转机械故障诊断进行了大量研究。为了提取轴承信号振动特征,LEI Y等人[4]采用经验模态分解(empirical mode decomposition,EMD)方法提取了轴承信号特征值,该算法基于故障信号的极值点形成包络曲线,并将其拆分成若干个内涵模态分量,以此来对信号进行重构和降噪;但EMD方法存在模态混叠和端点效应的问题。郑近德等人[5]采用了集合经验模态分解(ensemble empirical mode decomposi-tion,EEMD)的方法、杨斌等人[6]采用了互补集合经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)的方法、张淑清等人[7]采用完备集合经验模态分解(improved complete empirical mode decomposition,ICEMD)方法,分别对轴承的故障信号进行了处理,虽然以上一系列算法在一定程度上解决了模态混叠的问题,但仍然无法解决端点效应、计算量大和抗噪能力较差等问题。

由于采用小波变换对振动信号进行处理时,具有多分辨率特性和自适应性特点,其在振动信号处理方面得到了广泛应用。苏莹莹等人[8-9]采用小波变换的方法,对振动信号进行了时频分析,取得了一定的成果;但是小波变换方法只能处理单个信号,对多个信号的时频域特征仍难以处理。

为了解决上述问题,DRAGOMIRETSKIY K等人[10]提出了变分模态分解(variational mode decomposi-tion,VMD)方法。VMD是将一个信号分解成几个模态信号,通过不断的迭代求解,确定各模态信号的中心频率和有限带宽。VMD方法克服了EMD相关方法中存在的模态混叠、端点效应和计算量大等的问题。

唐贵基等人[11]研究了变分模态分解方法及其在滚动轴承故障诊断的应用,该研究使用VMD方法,成功地识别出了滚动轴承的早期故障特征。

TORRENCE C等人[12]提出了交叉小波变换(XWT)方法。XWT方法是建立在传统小波变换基础上的一种新型信号分析技术。GRINSTED A等人[13]将交叉小波变换方法应用于区域气候分析领域。XWT可以分析两个信号在时频空间中的相干性,并得到一个相关性频带;其频带亮度越高,两个信号在时频域的相关性就越强。由于噪声的随机特性,在交叉小波变换中,噪声在频带中的相关性最弱,可以被明显地识别出来,从而达到了降噪及增强信号的目的。

虽然VMD对采样点的个数和噪声具有较强的鲁棒性,但是分解之后的模态分量仍含有噪声。同时,XWT处理后的信号也会存在噪声。

因此,笔者提出一种基于IVMD-XWT联合去噪的信号处理方法,采用该方法去除原始信号中的背景噪声,从而达到增强轴承故障信号的目的。

1 算法基本原理

1.1 交叉小波变换

对于时域信号x(t),其连续小波变换的定义为:

(1)

式中:a—比例因子;τ—平移因子;*—复数共轭;ω0—x(t)的初始相位角;ψ(t)通常为Morlet小波函数。

ψ(t)的表达式为:

ψ(t)=π-1/4(e-jω0t-e-ω2/2)e-t2/2

(2)

对于信号x、y,其交叉小波变换为:

(3)

式中:Wxy(a,τ)—交叉小波相干谱密度,该值越高,信号x、y的相关性则越大。

1.2 变分模态分解

变分模态分解(VMD)的核心是构建和求解变分问题。假设每个模态都被紧凑地分布在中心频率周围,则VMD方法如下:

(1)对于给定信号,定义模态数量K和模态带宽控制参数a,并初始化模态uk(k=1,2,3,…K);

(2)对于每一模态uk(t),利用希尔伯特(Hilbert)变换,计算相关的解析信号,即:

(4)

(3)将每个模态的频谱移动到相应的估计中心频率。其表达式为:

(5)

(4)通过平方L2范数估计带宽;然后,引入二次惩罚项a和拉格朗日乘子因子λ(t)来表示无约束问题;最后,求解增广拉格朗日表达式的鞍点,并应用帕萨瓦尔定理进行计算。其计算式为:

(6)

其二次优化问题的解为:

(7)

1.2.1 改进变分模态分解

改进变分模态分解(IVMD)是利用包络谱来选取合适的K值。但VMD中的K值并没有明确的定义,在不知道信号的情况下,需要提前设定K的取值。因此,找到合适的K值较为困难,影响实验结果的准确性。

采用基于频谱包络的识别信号中有效频率分量的方法,可以确定VMD的最佳K值。

其步骤如下:

(1)将信号x进行傅里叶变换为:

F(s)=FFT(x)

(8)

Aax=|F(si)| (i=1,2,…,l)

(9)

式中:l—整数,值为数据x的一半。

(2)检测数据的局部极值;

(3)用三次样条插值法生成滤波谱的包络曲线;

(4)计算阈值,根据阈值滤除噪声和干扰分量,即:

Threshold=Al+r(Ah-Al)

(10)

式中:Ah—最大震级;Al—最小震级;r—控制阈值水平的比率,其值越大,阈值越高;r=0.2。

(5)通过将这些频率分量设置为零,过滤掉幅度小于阈值的频率分量;

(6)从得到的包络曲线中确定最佳模态数。

1.2.2 最佳参数值VMD降噪处理

为了验证最佳K值的有效性,笔者选取采样频率为12 kHz正常轴承振动信号进行分析,分别生成未改进VMD与IVMD时频图结果。

正常轴承的降噪处理结果如图1所示。

图1 正常轴承降噪处理结果

由图1可知:将未经改进的VMD和IVMD时频图结果,与信号的时间波形图进行对比,可以看出,正常轴承信号也存在一定噪声,但IVMD能有效地消除部分噪声。

1.3 KNN算法

K近邻(KNN)算法是一种监督学习的分类算法[14],同时也是一种原理易于理解、实现简单、分类清楚的算法[15]。

其基本原理为:定义一个训练样本,找到与训练样本距离最近的K个样本,然后对K个近邻样本进行预测,判断分类样本数据的类别。

KNN通常使用欧氏距离作为测量样本距离。

其定义为:

(11)

2 基于XWT-IVMD的特征提取方法

基于XWT和IVMD故障特征提取及诊断流程,如图2所示。

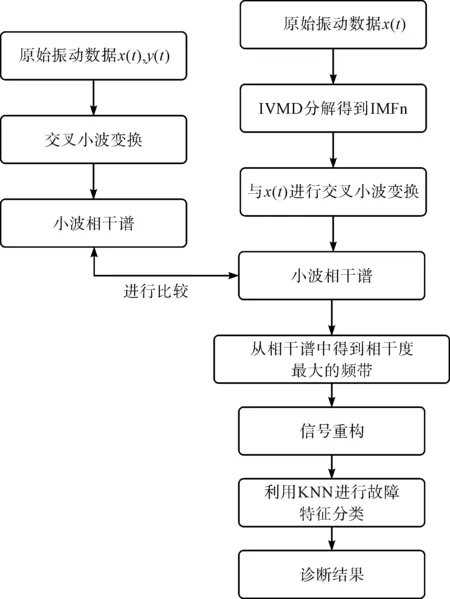
图2 基于XWT和IVMD的特征提取诊断流程图

具体方法步骤如下:

(1)将原始数据x(t)和y(t)进行交叉小波变换,得到小波相干谱图;通过观察小波相干谱,得到最相干频带,并记录相干频带在相干谱中的位置;

(2)选择两组信号中峭度值较大的信号(较大的峭度值代表信号中有更多的故障信息),对信号进行IVMD分解,得到IMF分量;

(3)将分解得到的IMF分量与峭度值较大的信号进行交叉小波变换,得到小波相干谱图;

(4)从分量小波相干谱图中寻找与原始小波相干谱图相干性最大的频带,删除相干性较差的频带,得到重构信号;

(5)将重构信号输入KNN,进行故障特征分类;

(6)根据结果判断该方法的特征提取效果。

3 实验及结果分析

3.1 实验数据采集

笔者使用Spectra Quest公司的轴承故障模拟试验台(MFS),采集实验数据,并对采集到的双通道内圈故障轴承信号进行分析。

其中,传感器的安装位置图如图3所示。

图3 传感器安装位置

笔者通过实验来模拟4种轴承类型,并采集信号样本,分别为:正常轴承、滚动子故障、内圈故障和外圈故障。每种类型样本长度为1 024,样本数量采集为100组,4种样本数据共400组。

4种轴承类型及样本采集数如表1所示。

表1 故障类型及采集样本数

3.2 实验结果分析

3.2.1 信号的重构

笔者以轴承内圈故障信号为例,得到采集的双通道内圈故障轴承信号的时域图和频域图,并对其进行XWT处理。

双通道内圈故障的时频信号如图4所示。

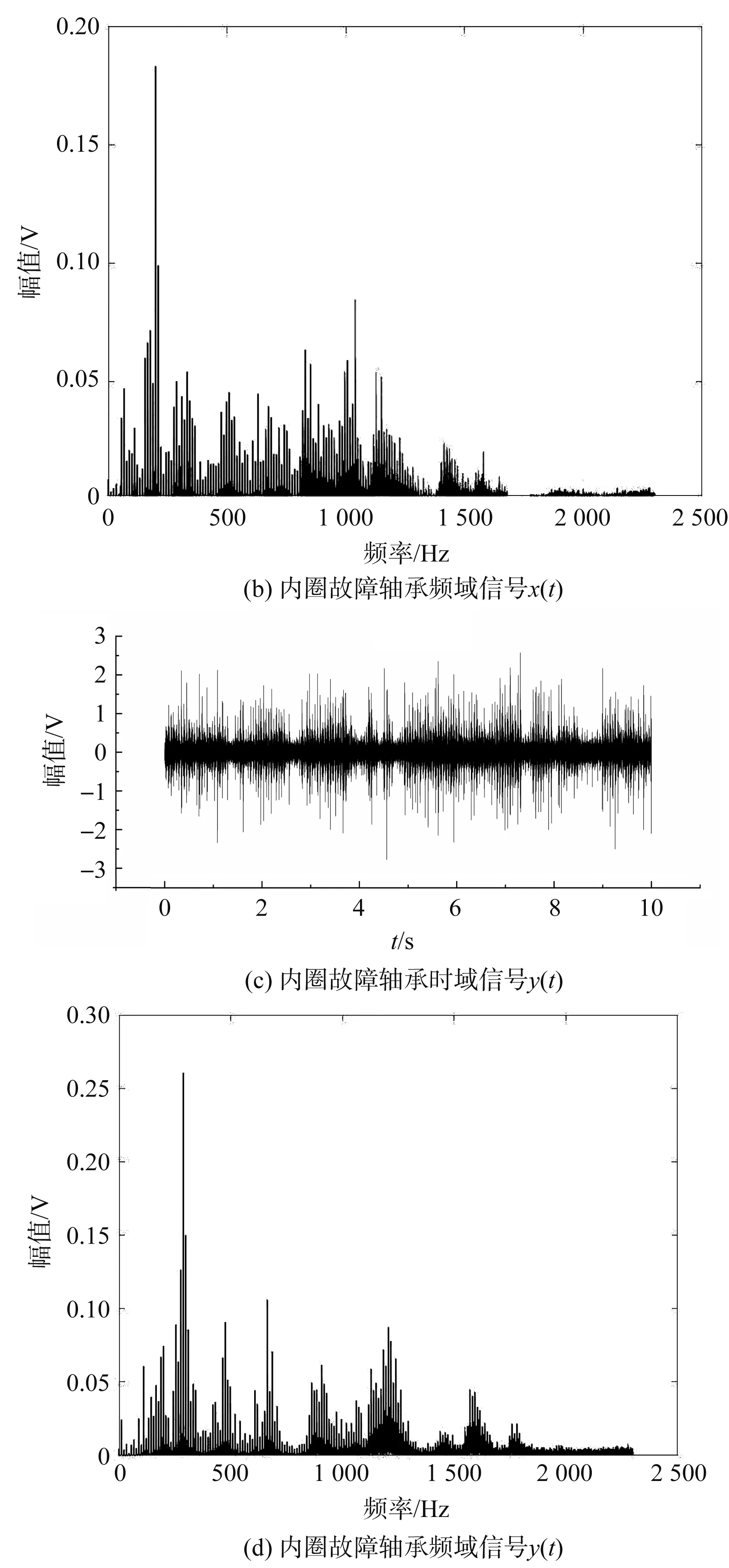
图4 双通道的内圈故障信号

由图4可知:只通过时域波形及其频谱不能识别滚动轴承内圈故障特征,因此,笔者将图4中的双通道信号再进行XWT处理,所得到的结果如图5所示。

图5 x(t)、y(t)的小波相干谱图

由图5可知:亮度较高的频带表示两个信号相关度较高,即含有更多的故障信息;暗度区域被认为是噪声区域,或含有故障信息较少。

笔者两组内圈故障信号进行对比,即根据峭度值越大,含有的冲击成分越明显,特征越容易提取的原则,计算x(t)、y(t)两个故障信号的峭度值,其结果如表2所示。

表2 x(t)、y(t)的峭度值

由表2可知:y(t)含有更多的故障信息,因此,笔者选择y(t)作为IVMD分解的原始信号,并通过上述方法对VMD分解过程中的K值进行选取,最后选择K值为8。

笔者对y(t)进行IVMD分解,将分解得到的8个分量分别与y(t)进行XWT处理,得到的小波相干谱如图6所示。

图6 IMF分量与y(t)的小波相干谱图

由图6可知:IMF3、IMF6和IMF7的频带与原始相干谱中最大相关频带基本一致,这些频带可以表示振动信号中含有的故障信息;其他IMF相关度不高,包含轴承故障信息较少。

因此,重构后的故障信号可以表示为:S′(t)=IMF3+IMF6+IMF7。

全部故障信号重构之后的故障信号结果,如表3所示。

表3 重构信号组成

笔者将重构的信号输入KNN进行验证,IVMD-XWT分类结果如图7所示。

图7 IVMD-XWT分类识别率

由图7可知:IVMD-XWT联合去噪方法将2个外圈故障识别成滚动子故障,将1个滚动子故障识别成外圈故障,其他样本识别结果全部正确,说明IVMD-XWT模型的联合降噪能力突出,在故障诊断识别中取得较好的结果,验证模型有效。

为了更加直观地描述IVMD-XWT的故障特征提取效果,笔者对实验结果进行t-SNE特征可视化。

IVMD-XWT可视化结果如图8所示。

图8 可视化结果图

由图8可知:IVMD-XWT模型的特征分类较为集中,说明其分类效果好,可分性较强。

3.2.2 实验对比

为了进一步验证IVMD-XWT模型的优越性,笔者采用传统方法构建两种模型,进行对比实验。第一个模型将IVMD之后的信号输入KNN,进行故障识别分类;第二个模型将VMD-XWT输入KNN,进行故障识别分类。

两种分类结果,即分类识别率如图9所示。

图9 对比方法故障诊断结果图

由图9可知:与IVMD的分类结果相比,IVMD结合XWT的故障诊断方法能更好地去除噪声,增强了振动信号的特征;VMD-XWT分类识别率要优于IVMD[16]。

不同故障诊断方法的诊断识别率如表4所示。

表4 不同故障诊断方法的诊断识别率

由表4可知:IVMD-XWT的故障诊断识别率为97.51%,与IVMD和VMD-XWT模型相比,其故障诊断平均识别率分别提高10.83%、4.62%;

与改进VMD的实验结果相比,XWT在重构信号方面能更好地剔除噪声信号,增强故障信号的特征;

与VMD-XWT的结果对比,说明确定K值的VMD能够明显增强故障特征,减少噪声对信号的干扰;

3种模型对比结果表明,IVMD-XWT模型能更好地提取故障特征,提高故障诊断的识别率。

4 结束语

轴承早期故障信号容易被淹没于噪声中,其故障特征难以被提取,为此,提出了一种基于IVMD-XWT的联合去噪处理方法。

该方法首先将原始信号进行了XWT,获得了相干频带;然后,利用IVMD对原始信号的频带进行了分段,生成了多个IMF,在从原始信号中去除非相干频带对应的IMF后,达到了消除噪声的目的;最后,利用实验数据对结果进行了验证。

研究结论如下:

(1)与VMD相比,IVMD选取了合适的K值,增加了分解精度,减少了噪声,增强了滚动轴承的故障特征;

(2)实验结果表明:与IVMD、VMD-XWT模型相比,IVMD-XWT方法在故障诊断测试实验中的识别率为97.51%,高于另外两种故障诊断模型,能更加有效地提取故障特征。

在工程实践中,滚动轴承出现的故障一般为复合故障。因此,在接下来的工作中,笔者将基于上述方法,针对滚动轴承的复合故障展开进一步的研究。