圆柱滚子轴承次表面裂纹区域应力分布规律研究*

党晓勇,师志峰,刘 静

(1.北京动力机械研究所,北京 100074;2.重庆大学 机械与运载工程学院,重庆 400044;3.西北工业大学 无人水下运载技术工业和信息化部重点实验室,陕西 西安 710072)

0 引 言

滚动轴承是舰船、高铁和航空航天装备的关键基础部件之一。

次表面裂纹是导致机械装备滚动轴承元件表面出现剥落失效的主要原因[1,2]。当滚动轴承出现次表面裂纹时,在循环应力作用下,裂纹会发生扩展,在一段时间后发生多次分叉,成为表面裂纹,造成轴承表面疲劳剥落,严重影响轴承的工作性能,甚至导致机械装备发生失效[3,4]。因此,需要开展次表面裂纹诱发的轴承内部接触特征研究,为轴承运行状态监测与早期故障特征识别提供参考。

针对次表面裂纹对滚动轴承接触特性的影响问题,KUMAR A M等人[5]研究了7075铝合金材料由于纯滚动接触疲劳引起的次表面裂纹的萌生规律;但是该研究中尚未考虑轴承滚子-滚道间的相互作用。LIU C R等人[6]研究了滚动轴承次表面裂纹的萌生及其影响因素;然而其研究中未考虑轴承内部的应力分布。WEN J S等人[7]采用线性有限元模型研究了球轴承次表面裂纹的扩展规律;但是该研究并未考虑次表面裂纹倾斜角度的影响。DENG S等人[8,9]采用有限元方法研究了球轴承次表面裂纹形状、深度和尺寸等因素对应力强度因子的影响规律;但该研究尚未考虑这些因素对应力分布区域深度和宽度的影响规律。BOMIDI J A R[10]建立了线性弹塑性有限元模型,研究了圆柱滚子轴承次表面裂纹的萌生及扩展规律;然而模型中没有考虑圆柱滚子轴承内部应力分布特性与次表面裂纹之间的相互影响作用。MOGHADDAM S M等人[11]运用有限元方法研究了轴承钢次表面裂纹的扩展规律。GUAN J等人[12]建立了Voronoi有限元模型,探讨了圆柱滚子轴承夹杂引起的次表面裂纹扩展规律;但是没有考虑不同裂纹形状与轴承载荷对滚道内部应力变化的影响作用。

上述工作主要研究轴承次表面裂纹的扩展规律。然后,裂纹引起的应力变化,将改变滚子与滚道的接触特性,从而导致轴承的振动特性发生变化,影响系统的工作性能。

笔者根据赫兹接触理论,建立滚子与滚道等效接触简化模型,采用有限元方法进行对比验证;根据圆柱滚子轴承次表面裂纹的实际形态特征,提出含次表面裂纹的滚子与滚道接触有限元计算模型,研究次表面裂纹的长度、宽度和倾斜度对裂纹区域应力分布的影响规律。

1 仿真模型建立

1.1 滚子与滚道等效接触模型

根据赫兹接触理论可知,双圆柱接触的模型可等效为单个滚子与弹性半空间体的接触模型。

圆柱滚子轴承的滚子与滚道接触的等效模型如图1所示。

图1 滚子与滚道等效接触模型Pmax—最大接触压力;b—接触半宽;Xp—接触中心位置;Hr—弹性半空间体高度

根据赫兹接触理论和圆柱滚子轴承的结构特征,可将理论上的无限区域的弹性半空间体截取为高度与实际滚道所在套圈的高度Hr一致,宽度为10b的矩形区域[13,14]。

b的计算公式如下:

(1)

式中:R1,R2—滚子和滚道的半径;Q—作用在轴承上的径向载荷;l—滚子等效接触长度;E′—等效弹性模量;b—用赫兹接触模型计算得到的接触半宽。

其中:

(2)

式中:E1,E2—滚子与滚道的弹性模量;ν1,ν2—滚子与滚道的泊松比。

此外,可将与滚道对应的滚子的半径等效为R,其值取为:

(3)

接触面的最大接触应力为:

(4)

接触面的椭圆应力分布为:

(5)

1.2 有限元接触算法与算例

轴承滚子-滚道等效接触模型的有限元建模包括潜在接触区域的选择、接触算法的选择和边界条件的设定。

由于轴承滚子与滚道的接触宽度随载荷的变化而发生变化,故在滚子与滚道接触的计算工况中,接触方式定义为面面接触形式。

在有限元计算时,笔者将滚道设置为目标面,将滚子设置为接触面。当滚道次表面存在裂纹时,在载荷作用下,滚子通过滚道的过程中,可能会导致裂纹的两个面也发生接触,因此,笔者在裂纹表面也建立了接触对。

有限元方法支持多种接触算法,常用的面面接触算法包括罚刚度法和增广拉格朗日算法。罚函数法是将接触非线性问题转化为材料非线性问题,在接触面之间利用接触弹簧单元建立连接关系。该弹簧刚度被定义为接触刚度。

其中,接触体的接触压力与接触变形(穿透量)尺寸之间的关系表示为[15]:

(6)

式中:P—接触压力;Kn—接触刚度。

其中:

Kn=FKN×K

(7)

式中:K—发生接触行为的基体单元刚度;FKN—惩罚刚度比例系数,取值范围为0.1～10;un—接触变形尺寸(穿透量)。

最大接触变形尺寸,由发生接触的单元深度h与穿透容差比例系数FTOLN所决定,其取值范围为0～1。根据有限元分析软件推荐值及前期计算经验,笔者确定FKN取值为1,FTOLN取值为0.1[16]。

另一方面,为了找到精确的拉格朗日乘子,利于采用拉格朗日算法对罚函数进行一系列修正迭代,其接触体的接触压力与穿透尺寸之间的关系可表示为:

(8)

其中:

(9)

式中:ε—输入容差;λi—第i次迭代的拉格朗日乘子分量。

对于目标面和接触面之间存在的摩擦应力,可由库仑定律获得[17]:

(10)

笔者以正常滚子与滚道接触状态下的圆柱滚子轴承N306为研究对象,选取理论接触半宽b为0.2 mm,将滚子-滚道等效接触模型与赫兹理想线接触模型获得的计算结果进行对比验证。

圆柱滚子轴承N306的几何参数如表1所示。

表1 圆柱滚子轴承N306的几何参数

对于理想线接触,滚子与滚道的长度相等,两者之间的变形可用公式表示为[18]:

(11)

式中:γ—滚子直径与节圆直径之比。

笔者采用Lundberg公式与有限元方法计算滚子与轴承正常内圈滚道接触变形δ、接触宽度Cw和接触应力σmax。其中,滚子等效半径为R=4.325 mm。

Lundberg公式与有限元方法计算结果的对比情况,如表2所示。

表2 Lundberg公式与有限元方法计算结果对比

由表2可知:作用在滚子的载荷从5 000 N增大到8 000 N,接触变形和接触宽度的误差<1%,最大接触应力误差接近6%,两者之间误差较小;采用两种计算方法(通过数值拟合的方式)计算得到的滚子与正常滚道的接触刚度分别为1.558 5×109N/m和1.557 1×109N/m,误差为0.87%。

上述结果表明:该有限元模型可用于圆柱滚子轴承滚子与滚道接触特性仿真计算。

1.3 次表面裂纹的有限元建模

当轴承滚道存在次表面裂纹时,该处滚子与滚道的接触特性会发生较大变化。次表面裂纹的存在会导致滚子轴承接触宽度、接触变形、接触应力和接触刚度产生变化,从而导致轴承振动加剧。

按照与滚道之间的角度,次表面裂纹可分为水平次表面裂纹和倾斜次表面裂纹。

圆柱滚子轴承次表面裂纹实图如图2所示。

图2 圆柱滚子轴承次表面裂纹实图

由图2可知:假设次表面裂纹贯通圆柱滚子轴承的滚道,在循环应力作用下,次表面裂纹会疲劳扩展,次表面裂纹逐渐扩展到滚道表面,直至引起表面剥落。

根据圆柱滚子轴承滚子-滚道等效接触模型,笔者建立了相应的有限元计算模型。

滚子-滚道等效接触有限元计算模型如图3所示。

图3 滚子-滚道等效接触有限元计算模型

图3中:滚子-滚道等效接触有限元计算模型中,椭圆位置的次表面裂纹包括:水平次表面裂纹、倾斜次表面裂纹和扩展裂纹。

笔者选取PLANE182单元,分别建立滚道和滚子的二维模型。

在有限元模型中,滚道的两边约束X向位移,滚道底部约束全部位移,滚子与滚道之间建立接触,目标单元与接触单元分别为TARGE169和CONTA172。其中,笔者在接触位置下方建立了裂纹,在接触位置对网格进行了加密处理,单元网格边长应不大于接触椭圆的半轴长度[19],单元尺寸取为1.5×10-3mm,远离接触位置的单元长度逐渐增大,单元数量为25 457,节点数量为23 486。载荷Q沿-y方向加载于圆柱滚子圆心处。

由文献[20]可知:由于循环载荷的作用,在滚动/滑动接触表面或次表面中形成的微小裂纹会扩展,从而造成其表面损伤;接触区径向载荷与接触表面垂直,与倾斜裂纹存在一定夹角,而裂纹扩展角度与表面牵引力的幅值大小存在关系。

考虑以上因素,笔者建立了次表面裂纹的有限元模型,如图4所示。

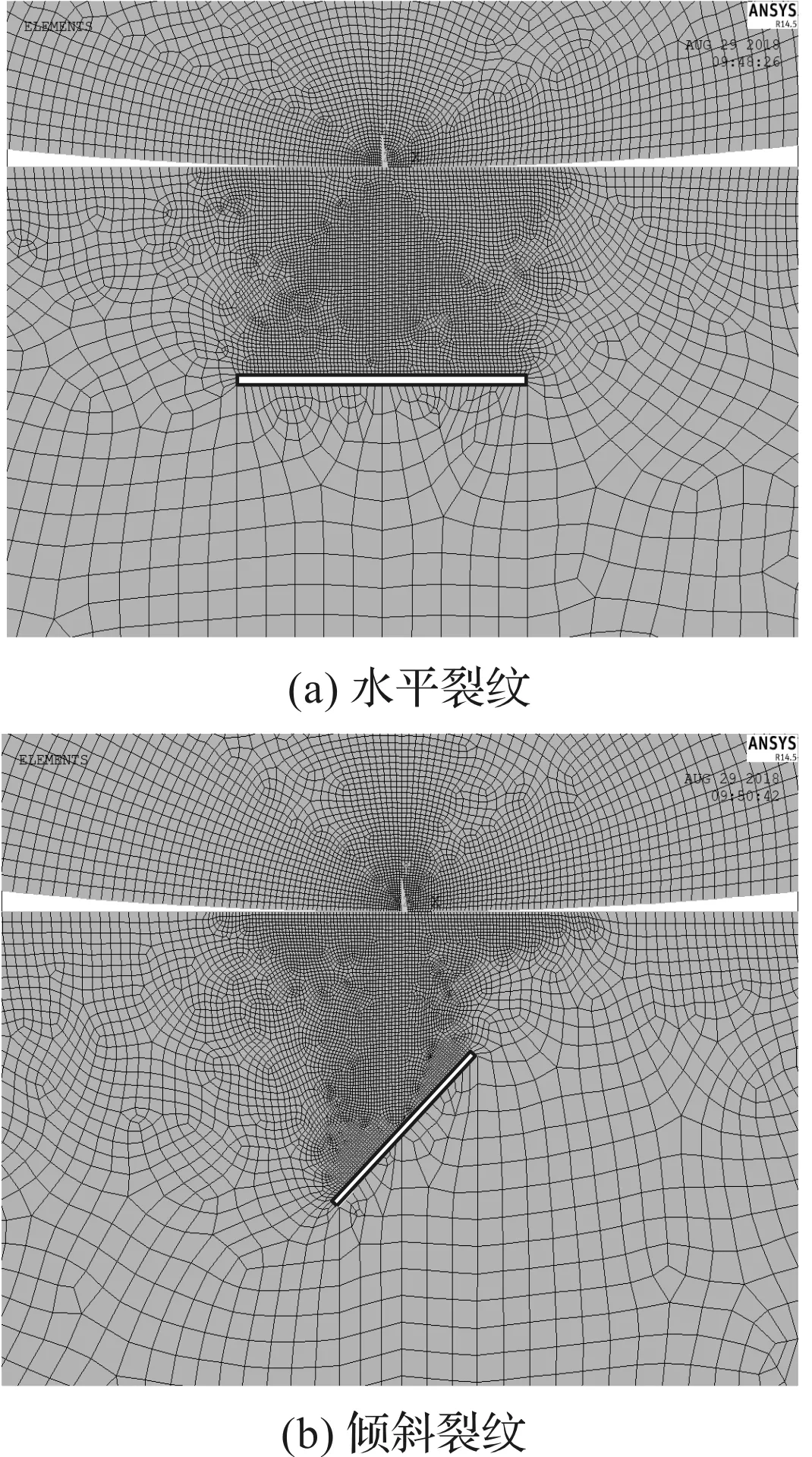
图4 次表面裂纹有限元建模

图4中:水平次表面裂纹和倾斜次表面裂纹采用一定长宽比的矩形代替,对于扩展裂纹,运用矩形与三角形组合的形式代替。

考虑到在有限元建模过程中,扩展裂纹的裂纹尖端容易出现应力集中,笔者采用KSCON命令,建立裂纹尖端应力集中点,使裂纹尖端的第一层单元变成奇异单元,用以模拟断裂奇异性。

2 仿真结果分析

当作用在滚子上的载荷发生变化时,滚子与滚道之间的接触宽度、接触变形、接触应力和接触刚度等随之发生变化,将导致轴承的工作状态发生改变。

当轴承滚道存在次表面裂纹时,滚道结构的变化会引起滚子与滚道接触状态发生改变;当施加在滚子上的载荷足够大时,载荷的循环作用导致次表面裂纹的扩展,从而引起轴承失效。

此处,笔者以圆柱滚子轴承N306为研究对象,研究不同类型次表面裂纹对轴承接触特性的影响。

2.1 水平次表面裂纹对滚道应力区的影响

水平次表面裂纹的示意图,如图5所示。

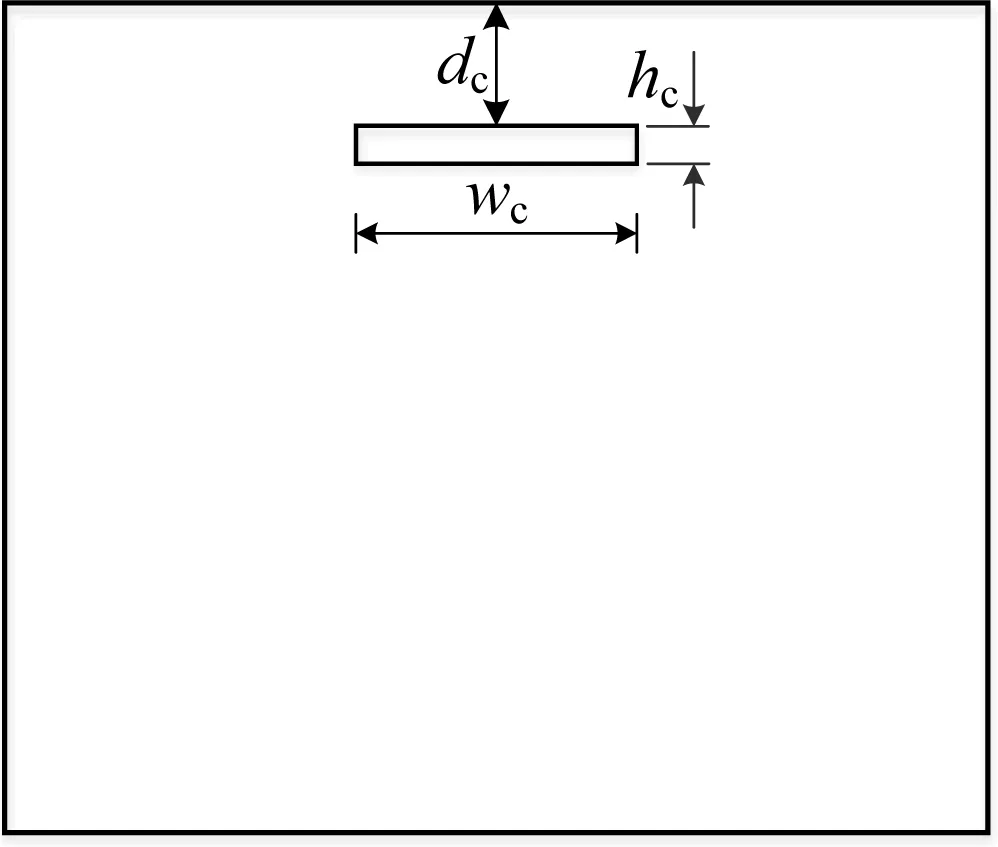
图5 水平裂纹dc—滚道上次表面裂纹的深度;wc—滚道上次表面裂纹的宽度;hc—滚道上次表面裂纹的高度

图5中:次表面裂纹高度hc取值与轴承材料的晶粒尺寸范围相关。

笔者选取hc=10 μm;接触半宽b取0.2 mm,略大于实际接触面半宽,与正常轴承滚子-滚道等效接触有限元计算模型一致,便于进行比较。

笔者以1 GPa为应力边界范围,等效应力大于1 GPa的应力区为研究对象,研究滚道次表面等效应力分布。

次表面裂纹状态下的滚道次表面应力分布如图6所示。

图6 滚道次表面等效应力分布d—裂纹一端应力区的深度;w—裂纹一端应力区的宽度

由图6可知:次表面裂纹的存在,会引起次表面裂纹周围应力的增大,尤其在裂纹尖端位置,一般会因为应力的极端增大而导致裂纹扩展;在接触区,应力在裂纹尖端幅值大,主应力分布在裂纹尖端两侧,且表面靠近裂纹尖端一侧的应力数值更大。

2.1.1 次表面裂纹深度对应力区的影响

此处,水平次表面裂纹深度取为0.5b,1b,1.5b,2b和2.5b,b=0.2 mm;宽度取为2b。

应力区宽度和深度的变化规律,如图7所示。

图7 水平次表面裂纹深度对应力区的影响

由图7可知:当载荷增大时,应力区的深度和宽度都有不同幅度的增大;当次表面裂纹深度增大时,应力区的深度和宽度都迅速降低。

2.1.2 次表面裂纹宽度对应力区的影响

水平次表面裂纹宽度取为0.5b,1b,1.5b,2b和2.5b,b=0.2 mm;深度取为b。

应力区宽度和深度的变化规律,如图8所示。

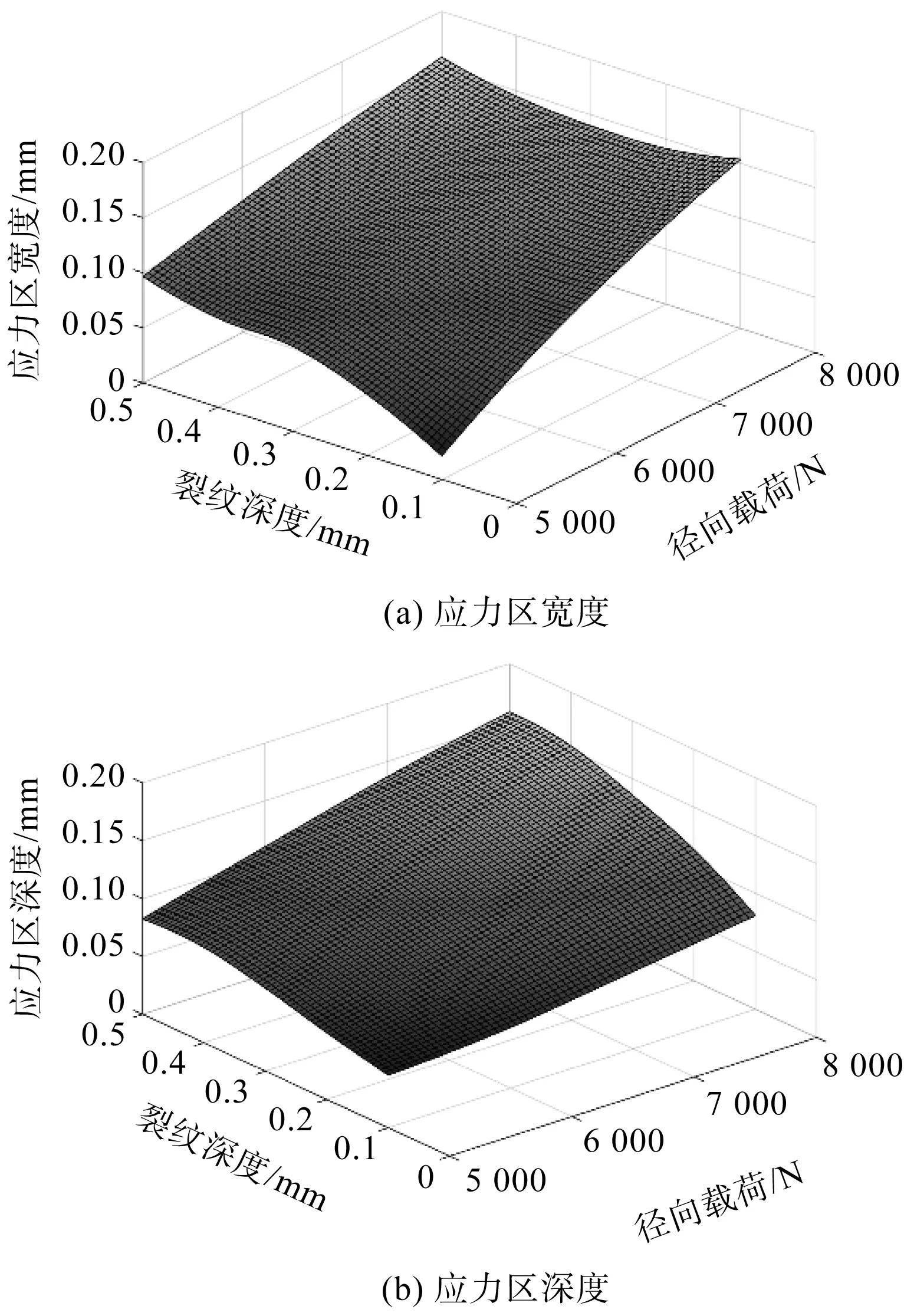
图8 水平次表面裂纹宽度对应力区的影响

由图8可知:当载荷增大时,应力区的深度和宽度都有不同幅度的增大;当次表面裂纹的宽度增大时,应力区的深度和宽度都迅速增大。

2.2 次表面裂纹对滚道应力区的影响

倾斜次表面裂纹的示意图如图9所示。

图9 倾斜次表面裂纹dc—滚道上次表面裂纹的深度;wc—滚道上次表面裂纹的宽度;hc—滚道上次表面裂纹的高度;α—倾斜次表面裂纹与滚道表面的夹角(倾斜角)

笔者以1 GPa为应力边界范围,等效应力值大于1 GPa的应力区为研究对象,分析裂纹深度较大的裂纹尖端位置的应力区。

次表面裂纹状态下的滚道次表面应力分布,如图10所示。

图10 滚道次表面等效应力分布d—裂纹一端应力区的深度;w—裂纹一端应力区的宽度

由图10可知:倾斜次表面裂纹的存在,会引起次表面裂纹周围应力的增大,倾斜裂纹会引起应力分布区的变化,尤其在裂纹尖端位置,一般会因为应力的极端增大和反复作用而导致裂纹扩展;接触区径向载荷与接触表面垂直,与倾斜裂纹存在一定夹角,而裂纹扩展角度与表面牵引力的幅值大小存在一定的关系。

2.2.1 次表面裂纹倾斜角对应力区的影响

倾斜次表面裂纹的深度与宽度均取为b;次表面裂纹倾斜角分别为0°,22.5°,45°,67.5°和90°。

倾斜次表面裂纹对滚道应力区的影响如图11所示。

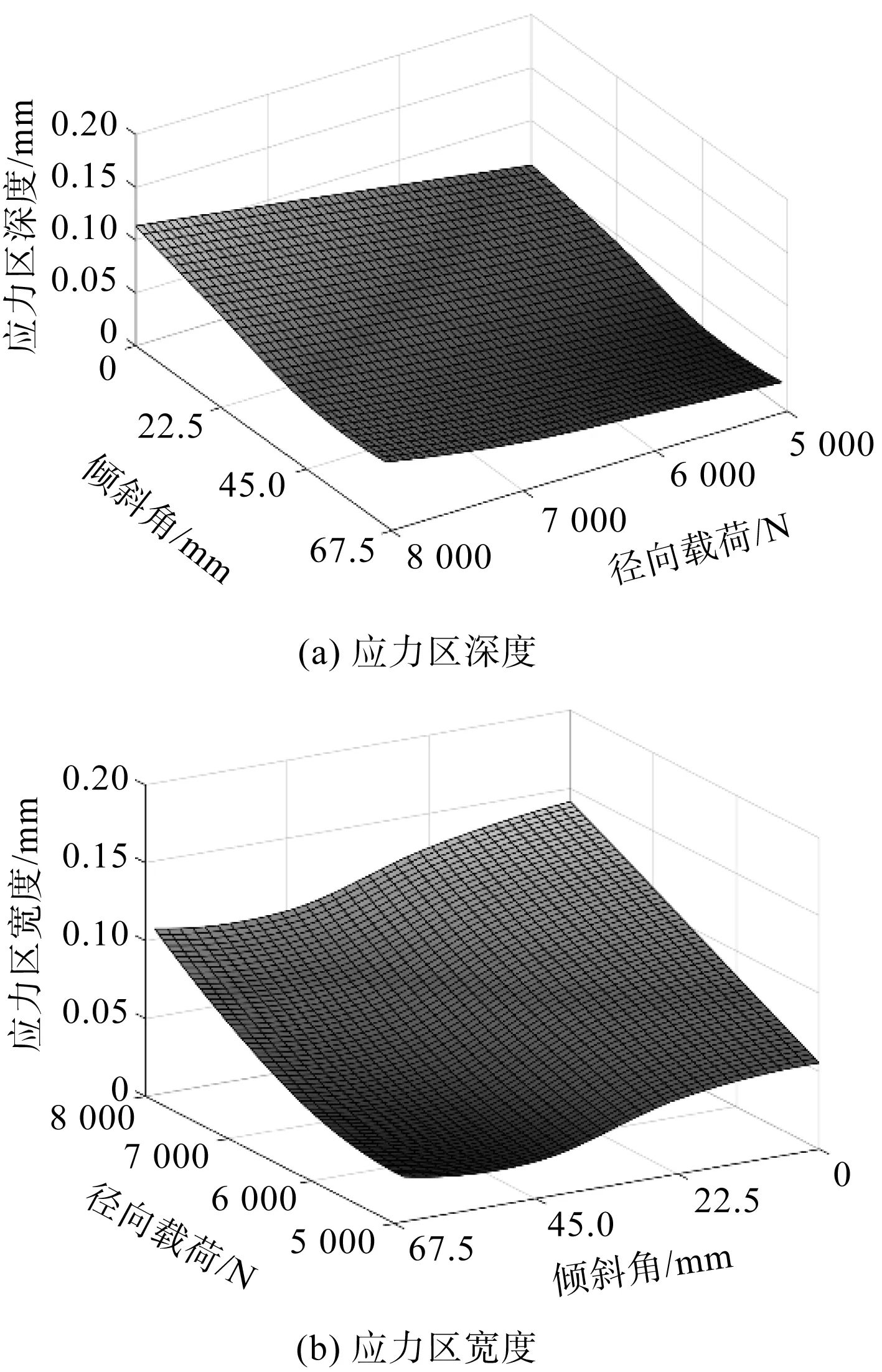
图11 倾斜次表面裂纹对滚道应力区的影响

由图11可知:当倾斜次表面裂纹的倾斜角增大时,次表面裂纹两端的应力分布区发生位置变化,应力区的宽度和深度都有不同程度的减小。

倾斜角为90°时次表面等效应力分布如图12所示。

由图12可知:倾斜角持续增大直至接近90°时,次表面裂纹下端的应力区逐渐消失,裂纹上端的应力区减小。

上述结果表明:当次表面裂纹的高度与宽度一定时,次表面裂纹的倾斜角越大,次表面应力区越小,次表面裂纹对轴承的影响也小。

2.2.2 次表面裂纹宽度对应力区的影响

倾斜次表面裂纹的深度hc取为b;倾斜角α取为45°;宽度wc分别取为b,1.2b,1.6b,1.6b和1.8b;作用于滚子上的径向载荷取5 000 N,6 000 N,7 000 N和8 000 N。

倾斜次表面裂纹宽度对应力区影响如图13所示。

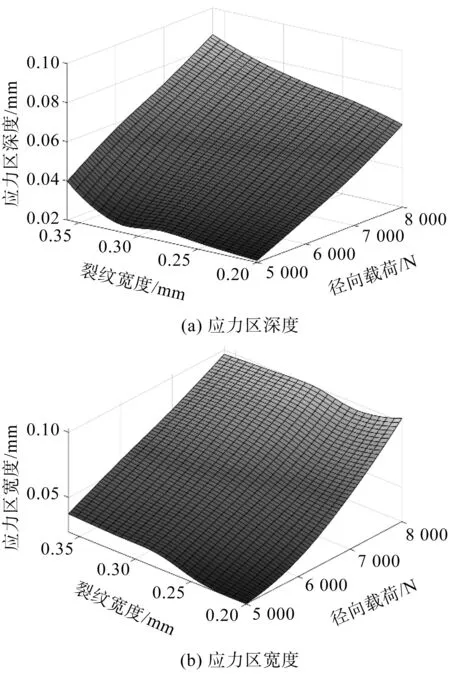
图13 倾斜次表面裂纹宽度对应力区影响

由图13可知:(1)载荷对滚道次表面应力区的影响明显,应力区的深度和宽度随着载荷的增大而增大;(2)次表面裂纹尖端的应力区还受次表面裂纹宽度的影响,次表面应力区的宽度与深度随次表面裂纹宽度的增大而增大,次表面应力区的深度相比于宽度变化更明显。

3 结束语

根据赫兹接触理论,笔者建立了滚子与滚道等效接触简化模型;采用有限元方法,建立了滚子与正常滚道等效接触有限元计算模型,并将其仿真计算结果与采用赫兹接触理论获得的结果进行了对比验证;根据圆柱滚子轴承次表面裂纹的实际形态特征,提出了含次表面裂纹的滚子与滚道接触有限元计算模型,研究

了次表面裂纹的长度、宽度和倾斜度对裂纹区域应力分布的影响规律。

研究结果表明:

(1)当载荷增大时,应力区的深度和宽度都有不同幅度的增大;当次表面裂纹的深度增大时,应力区的深度和宽度都迅速降低;当次表面裂纹的宽度增大时,应力区的深度和宽度都迅速增大;

(2)倾斜角持续增大直至接近90°时,次表面裂纹下端的应力区逐渐消失,裂纹上端的应力区减小;

(3)当次表面裂纹的高度与宽度一定时,次表面裂纹的倾斜角越大,次表面应力区越小,次表面裂纹对轴承的影响也小。载荷对滚道次表面应力区的影响明显,应力区的深度和宽度随着载荷的增大而增大;次表面裂纹尖端的应力区还受次表面裂纹宽度的影响,次表面应力区的宽度与深度随次表面裂纹宽度的增大而增大,相比于宽度的变化,次表面应力区的深度变化更明显。

含次表面裂纹的滚子与滚道接触有限元计算模型能够用于研究分析次表面裂纹的长度、宽度和倾斜度对裂纹区域应力分布的影响规律,但是在裂纹破坏性发展的预测方面还存在一定难度。

笔者后续将基于断裂力学理论,结合应力集中因子(stress intensity factor,SIF),进行裂纹破坏性发展的研究。