基于工业机器人动力学模型的差分力矩偏差碰撞检测方法*
2023-03-10张振宇钟佩思王祥文孙钰雁
张振宇 钟佩思 张 超 王祥文 刘 梅 孙钰雁
(①山东科技大学先进制造技术研究中心,山东 青岛 266590;②山东科技大学机械电子工程学院,山东青岛 266590;③青岛海信日立空调系统有限公司,山东 青岛 266510)
随着机器人技术的发展,工业机器人之间、工业机器人与人之间的协作越来越密切,在协作的过程中难免会发生机器人与入侵物体的碰撞。因此需要准确地进行碰撞检测,以避免碰撞事故的发生。工业机器人的碰撞检测可分为使用外部传感器和不使用外部传感器的碰撞检测[1−3]。不使用外部传感器时,采用基于动力学模型的方法来实现碰撞检测,通过动力学模型计算相应的预测力矩,将预测力矩与实际力矩的力矩偏差值用于碰撞检测[4]。机器人的实际力矩是通过电流法来计算关节力矩,通过伺服电机相电流来求得电机实际输出驱动力矩[5]。采集的机器人实时位置、速度及电机电流等存在噪声影响,因此有效的滤波方案能够获得精确的预测力矩和实际力矩。
基于动力学模型的碰撞检测方法,是在获得准确动力学参数的基础上完成的,因此需要准确的机器人动力学参数,动力学参数的准确性影响着碰撞检测的精度。现有机器人的动力学参数获取,通过动力学参数辨识获得。动力学参数辨识的过程可分为以下5个步骤:(1)建立动力学模型;(2)设计激励轨迹;(3)采样与数据处理;(4)动力学参数辨识;(5)验证辨识模型[6]。从动力学模型辨识过程中能够看出,设计良好的激励轨迹,采用准确度更高的动力学参数辨识方案,将获得接近真实值的机器人动力学参数。通过遗传算法优化激励轨迹,但是易陷入局部最优解[7−8]。改进的遗传算法能够有效避免陷入局部最优解,并在多个领域应用[9−10]。动力学参数辨识常用的方法是最小二乘法[11],但是最小二乘法容易受到噪声的干扰,由此提出递推最小二乘法、加权最小二乘法等方法来进行动力学参数辨识[12−13],均需要观测矩阵求逆,而观测矩阵存在奇异值情况下无法求逆,效果较差;Urrea C等提出采用线性神经网络进行机器人动力学参数辨识的方法[14−15],但神经网络受学习率的影响较大,学习率过大会导致无法收敛,学习率过小容易陷入局部极值点,而自适应学习率能够使得神经网络快速收敛的同时避免陷入局部极值。
本文针对机器人在动力学模型未知的情况下,通过动力学参数辨识,获得机器人准确的动力学模型,然后通过机器人的动力学模型计算机器人预测力矩,将预测力矩与实际力矩做差获得力矩偏差,力矩偏差分别向后一阶差分、向后二阶差分,通过设定的阈值来检测是否发生碰撞和发生碰撞类型。在动力学参数辨识中,采用基于惩罚函数的自适应遗传算法优化激励轨迹,利用自适应学习率的单层神经网络进行动力学参数辨识。采用力矩偏差差分的碰撞检测方法不仅实现无外部传感器碰撞检测,同时将碰撞的类型区分为有意碰撞和无意碰撞;通过区分碰撞类型,能够在机器人发生无意碰撞时,人为干预将无意碰撞转化为有意碰撞,从而避免发生刚性碰撞造成机器人损伤。实验结果表明,设计的碰撞检测算法,不需要添加额外的传感器,降低碰撞检测成本,能够准确地将碰撞区分为有意碰撞和无意碰撞,所采用的动力学参数辨识方法,辨识精度较其他方法有所提高,从而提高碰撞检测的精度。基于工业机器人动力学模型的差分力矩偏差碰撞检测算法的流程如图1所示。

图1 碰撞检测算法流程图
1 机器人动力学模型建立与线性化
1.1 动力学模型建立
建立n连杆机器人的动力学模型为
1.2 动力学模型线性化
由于标准动力学模型具有非线性强耦合的特点,直接利用该模型进行动力学参数辨识异常困难[16],因此将机器人的动力学模型进行线性化,可表示为:
借助Python环境下的SymPyBotic工具箱求解机器人的动力学最小参数矩阵和机器人各关节力矩表达式。
2 基于惩罚函数的自适应遗传算法优化激励轨迹
2.1 激励轨迹选择
机器人运行激励轨迹时达到的位姿越多,测得动力学参数信息越全面,动力学参数辨识的精度就会越高。Swevers J使用有限傅里叶级数对机器人进行激励轨迹设计,方便易用的同时,能够保证较好的辨识效果,被广泛使用,且傅里叶级数能够减少噪声对参数精度的影响[18]。第i关节傅里叶级数公式为
式中:i是机器人连杆的编号;q0i是关节的初始位置;M是傅里叶级数;ai,k、bi,k为正弦项和余弦项的系数;ω=2πf为基角频率。为使得关节初始位置变化平稳,设q0i为式(8)。
根据式(7)获得机器人关节i的角速度和角加速度为式(9)和式(10)。
为使得激励轨迹运动范围充满整个运动空间,达到最好激励效果,在对激励轨迹进行参数优化时,优化目标函数为观测矩阵最小条件数[19]。条件数是线性方程组解对输入输出误差敏感性的测量,条件数越大表明敏感性越差,因此将观测矩阵条件数最小作为优化目标函数。
设关节i的傅里叶轨迹参数向量Ri=[ai,1,bi,1,...,则所有关节的激励轨迹参数向量R=轨迹采样点数为K个,非线性优化问题可表示为:
式中:qimax是关节i的位置限制;是关节i的速度限制;是关节i的加速度限制。
式中:tstart、tend为轨迹起始时刻和结束时刻。
2.2 基于惩罚函数的自适应遗传算法原理
通过增加惩罚函数,能够将约束问题转化为无约束问题。因此在遗传算法中加入惩罚函数以增大适应度,进行排列后,将增大后的个体剔除。自适应机制将交叉概率和变异概率自适应调整,如图2所示。
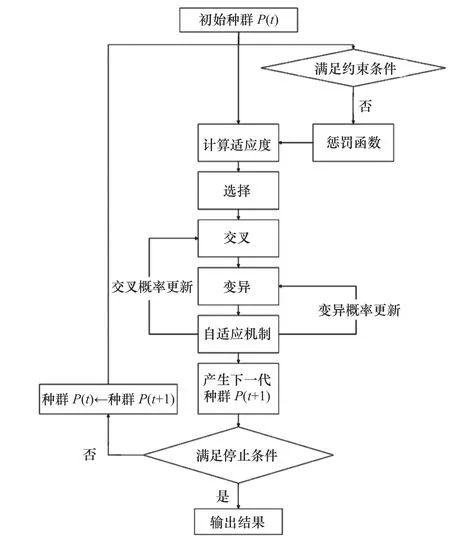
图2 基于惩罚函数的自适应遗传算法原理图
(1)初始种群:随机生成初始种群。
(2)适应度函数:适应度函数是评价个体好坏的标准,是非负的值。在动力学参数辨识中,采用观测矩阵的最小条件数作为适应度函数。
(3)惩罚函数:根据动力学参数辨识的需要,设计动态惩罚函数。如:
式中:λ是惩罚因子;α是动态偏差因子(不满足约束条件的解偏离约束差值的平均值);b为经验常数;t(R)是个体满足线性条件和非线性条件的个数。
(4)选择:选择是从父代种群中选出优化的个体来产生下一代,采用最佳保留选择,因为条件数作为适应度函数,因此条件数越大则适应度越小,因此选择适应度函数值低的个体,排除适应度函数值高的个体。
(5)交叉与变异:交叉与变异的概率有固定概率和动态概率2 种方式,动态概率是能够随着算法的迭代概率也随之变化。采用动态概率,以实现交叉概率与变异概率的自适应调整。概率的调整函数为
其中:k1、k2分别为交叉和变异的经验常数,则k1=1、k2=0.5。fmin、fmean分别为种群的适应度函数的最小值和平均值。
交叉选择算术交叉,变异采用高斯变异。
3 采用自适应学习率的单层神经网络实现动力学参数辨识
3.1 实验数据采集与处理
采集的位置、速度及电流信号存在的噪声将对参数辨识结果产生影响,且加速度是由速度差分获得,差分会成比例放大噪声,同时为了防止经过滤波后的数据产生相位延时,采用零相位滤波以避免产生延时。具体滤波方案如下:
(1)位置:巴特沃夫斯低通滤波+零相位滤波。
(2)速度:巴特沃夫斯低通滤波+零相位滤波。
(3)加速度:巴特沃夫斯低通滤波+零相位滤波+RLOESS平滑。
(4)力矩:巴特沃夫斯低通滤波+零相位滤波+RLOESS平滑。
3.2 神经网络算法
单层神经网络通过1个输入层计算后获得输出层,通过对每个输入进行加权求和(w),再通过激活函数f(x)得到对应的输出,如图3所示。
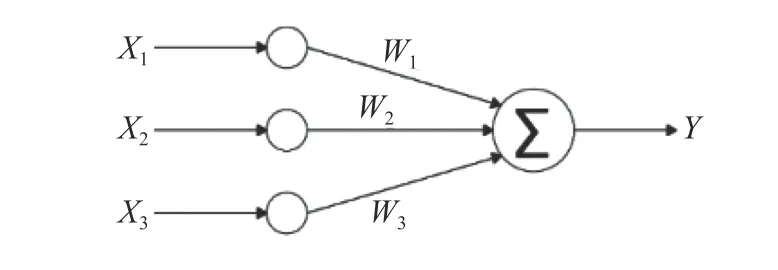
图3 单层神经网络
将观测矩阵的每1行作为单层神经网络的输入,输出为每一行对应的力矩值。更新的权重W为辨识的参数,激活函数为f(x)=x。
权重更新方法为
式中:dw为权重增量;β为超参数;α为学习率;e为实际力矩值与预测力矩值的差值;κ为经验常数;X为观测矩阵的某一行。
将学习率依据实际力矩与辨识后的预测力矩值的差值进行自适应调整。加入自适应学习率,能够提高神经网络的学习效果防止陷入局部最优解,同时能够避免无法收敛。
4 基于差分力矩偏差的碰撞检测算法
4.1 碰撞检测算法原理
通过辨识的动力学参数获得机器人预测力矩,利用机器人驱动电流信号计算实际力矩,将预测力矩与采集的实时力矩做差,获得力矩偏差。
依据辨识机器人的动力学参数,根据式(16)能够计算出机器人预测力矩。
式中:τe为 摩擦力矩;为机器人的力矩。
将预测力矩与实际力矩τreal做差获得力矩偏差:
根据图4a所示的力矩偏差变化图能够看出,在有意碰撞是入侵物体有准备地与机器人发生碰撞,接触缓慢且缓和,机器人力矩偏差变化也会缓慢,而无意碰撞力矩变化较为急剧。采用差分方程能够获得力矩偏差的变化趋势。差分方程分为向前差分、向后差分、中心差分,因为要在机器人碰撞瞬间能够快速检测碰撞,采用向后差分方程。
f(xk−1)、f(xk)、f(xk+1)一阶向后差分方程为:
因此,力矩偏差的一阶向后差分公式可表示为:
依据式(20)获得力矩偏差的一阶向后差分。如图4b为一阶力矩偏差差分变化图。因为差分方程能够放大噪声,因此采取无延时滤波处理。从图中看出,有意碰撞一阶力矩偏差值变化较为平缓,而无意碰撞变化较为明显,能够有效区分出有意碰撞与无意碰撞。考虑到碰撞力矩较小,引起的力矩偏差较小,因此将力矩偏差进行二阶力矩偏差差分,从而获得更为准确的碰撞检测时刻。
对于f(xk−1)、f(xk)、f(xk+1)则二阶向后差分方程为:
因此,力矩偏差的二阶向后差分公式可表示为
式(21)、(23)在t−1<0,t−2<0时,设∆τ(t−1)、∆τ(t−2) 等于∆τ(t)。
依据式(23)获得力矩偏差的二阶差分。如图4c所示,能够看出在无意碰撞阶段力矩偏差二阶差分变化较为明显,但在初始与结束阶段,变化也较为明显,因此需结合一阶力矩偏差差分进行力矩碰撞检测。
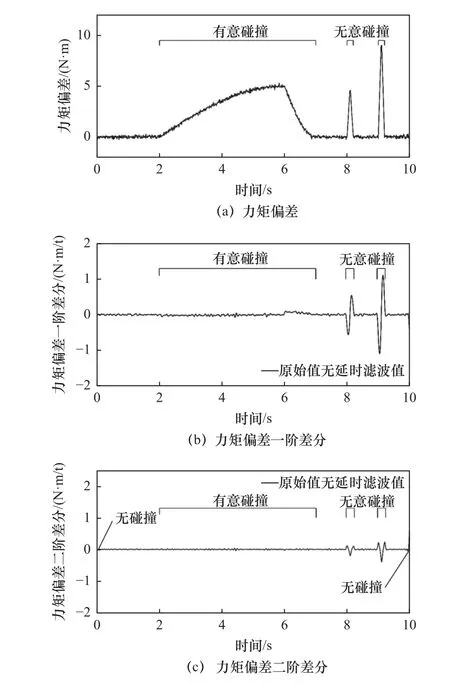
图4 力矩偏差及一阶二阶差分
通过设置合理的置信区间,当力矩偏差、一阶力矩偏差差分、二阶力矩偏差差分超出置信区间则认为机器人发生有意碰撞或无意碰撞,此时机器人采取相应的动作,防止碰撞力进一步增大,从而避免损失。
5 动力学参数辨识与碰撞检测实验
5.1 动力学参数辨识实验
利用6R工业机器人进行相关激励轨迹的设计,采用基于惩罚函数的自适应遗传算法优化激励轨迹,优化后的激励轨迹关节位置、关节速度、关节加速度如图5所示。从图中能够看出均满足约束条件,且速度与加速度的初始和结束均为零,满足激励轨迹优化的目标要求,能够有效实现6R机器人在关节空间内达到多种位姿,从而能够获得准确的机器人动力学参数。
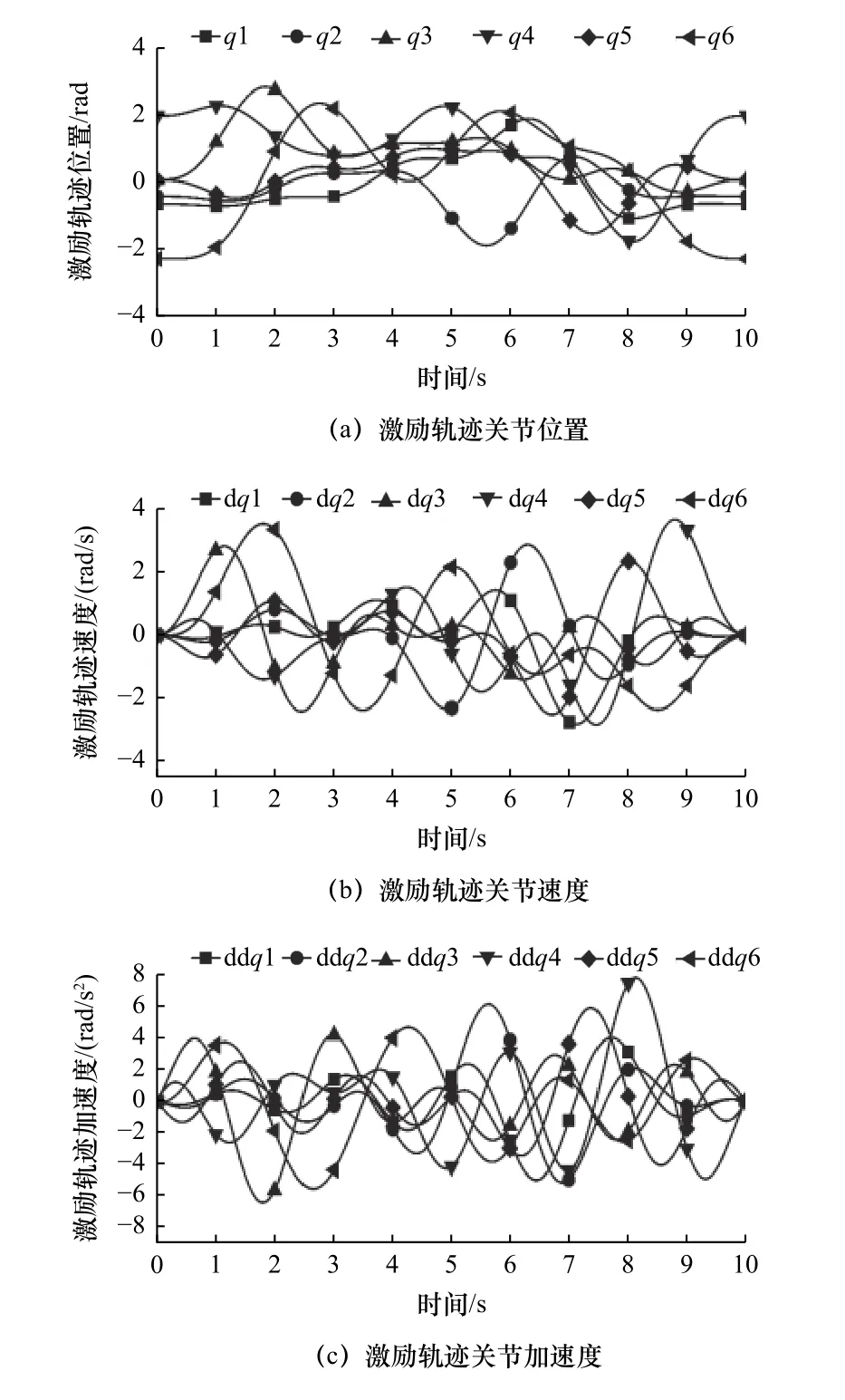
图5 激励轨迹位置、速度、加速度
将6R机器人运行激励轨迹后采集的数据进行滤波处理后,利用自适应学习率的单层神经网络进行动力学参数辨识。为了验证辨识参数的准确性,随机生成满足约束的1条轨迹,将辨识力矩与实际力矩进行对比,并利用均方根误差来对比辨识力矩和实际力矩型之间误差进行描述,其表达式为:
辨识力矩与实际力矩的对比如图6所示。各关节的力矩均方根误差如表1所示。
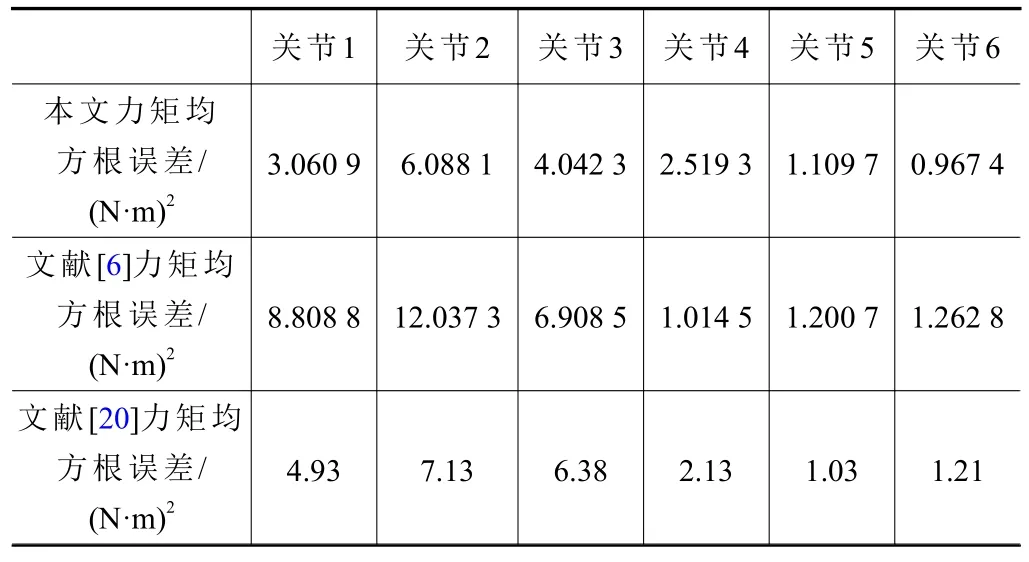
表1 各关节误差
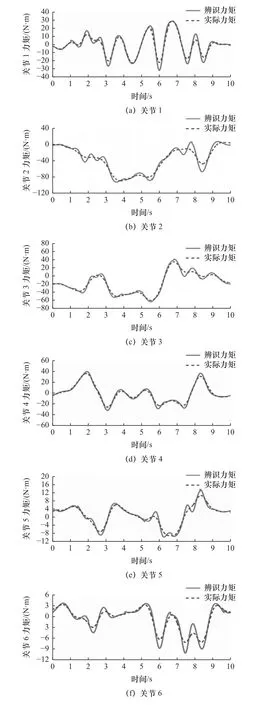
图6 辨识力矩与实际力矩对比
对比发现,采用自适应学习率的单层神经网络进行工业机器人动力学参数辨识,辨识精度通过均方根误差能够看出有所提高。同时也证明采用基于惩罚函数的自适应遗传算法优化激励轨迹有效。得到的动力学参数能够满足碰撞检测的需要。将获得的动力学参数应用于碰撞检测算法。
5.2 差分力矩偏差碰撞检测实验
利用辨识的动力学参数,结合获取的实际位置、实际速度、预测位置、预测速度、电机的电流信号及差分获得的实际加速度、预测加速度计算出实际力矩与预测力矩。将实际力矩与预测力矩加入碰撞检测算法中,利用6R工业机器人开展碰撞检测实验。首先将6R工业机器人运行多次,采集无碰撞状态下的位置、速度信号,从而获得无碰撞状态下的实际力矩信息,从而获得该机器人的碰撞置信区间,如表2所示。碰撞状态检测条件如表3所示。依据表2和表3结合差分力矩偏差碰撞检测算法对6R工业机器人的各个关节分别进行碰撞实验。碰撞过程如图7所示,为机器人6 个关节在不同状态下的碰撞,关节1为大阻力无意碰撞状态,关节2为微阻力无意碰撞状态,关节3为小阻力有意碰撞状态,关节4为小阻力无意碰撞状态,关节5为大阻力有意碰撞状态,关节6为小阻力有意碰撞状态

图7 碰撞过程

表2 关节置信区间
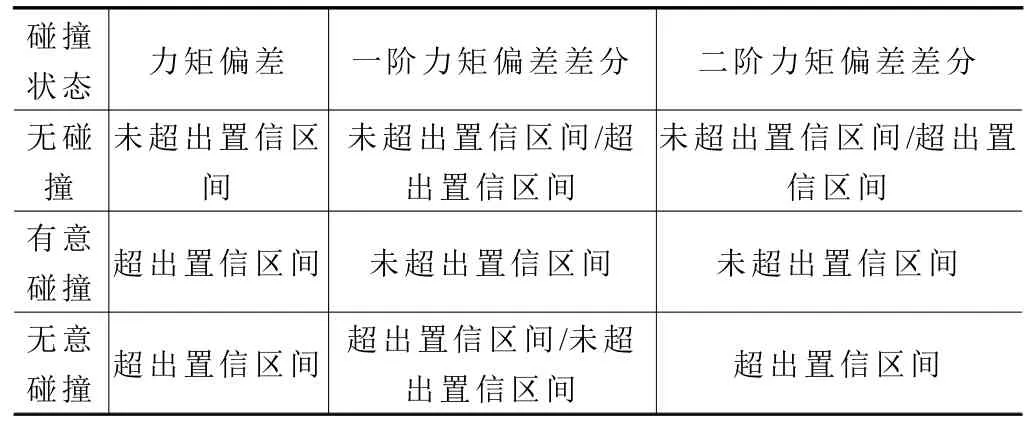
表3 碰撞检测条件
图8~13为碰撞检测算法的实验结果,图8为大阻力无意碰撞检测,从图中能够看到检测碰撞为无意碰撞;图9为微阻力无意碰撞检测,从图中能够看到检测碰撞为无意碰撞;图10为小阻力有意碰撞检测,从图中能够看到检测碰撞为有意碰撞;图11为微阻力有意碰撞检测,从图中能够看到检测碰撞为有意碰撞;图12为小阻力无意碰撞检测,从图中能够看到检测碰撞为无意碰撞;图13为小阻力有意碰撞检测,从图中能够看到检测碰撞为有意碰撞。因此验证碰撞算法能够对于有意碰撞与无意碰撞能够进行有效检测和区分,区分精度高,不需要在机器人外部添加额外的传感器。
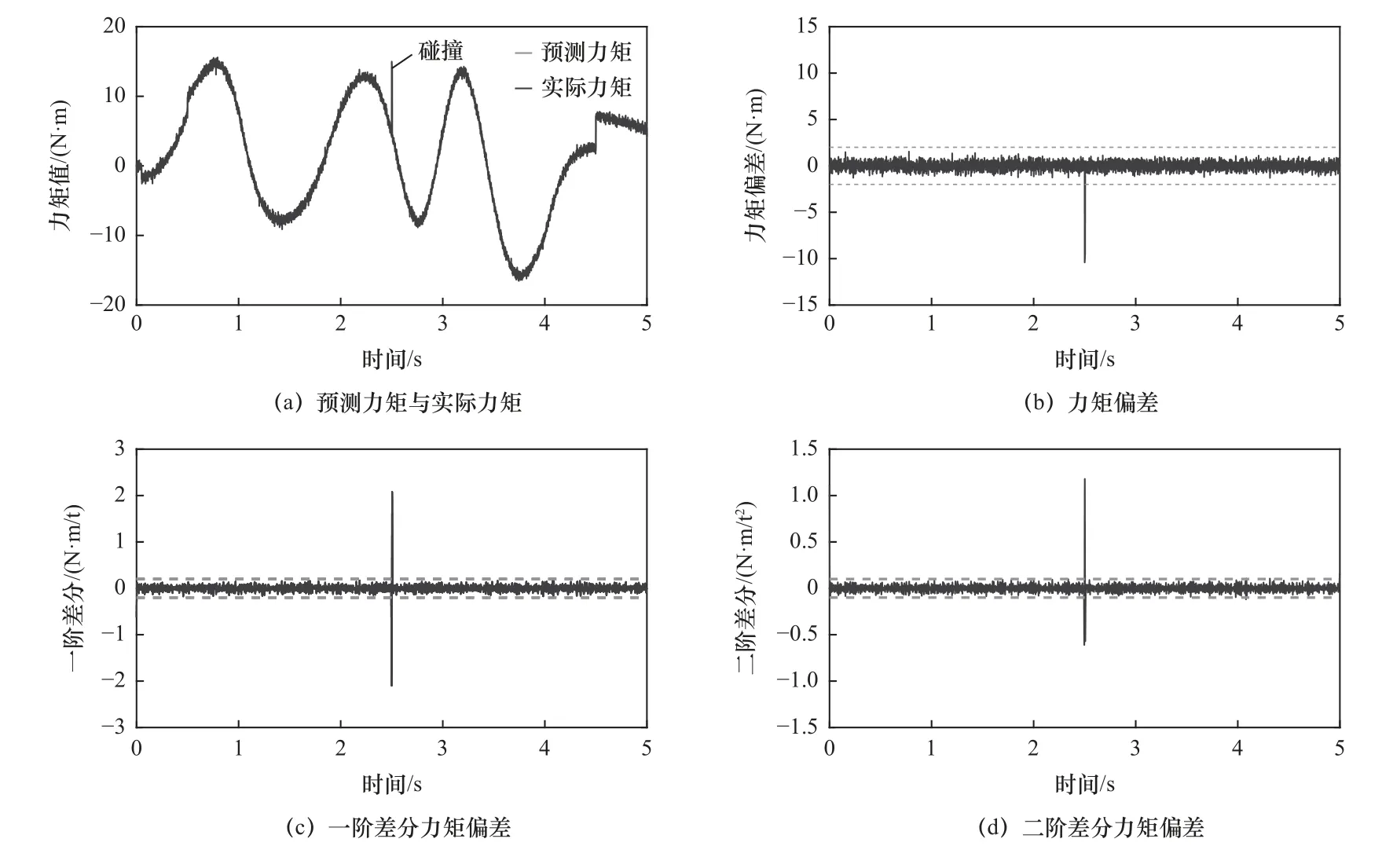
图8 关节1碰撞检测
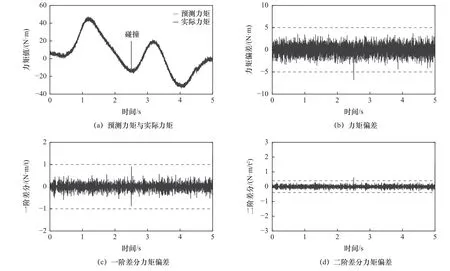
图9 关节2碰撞检测
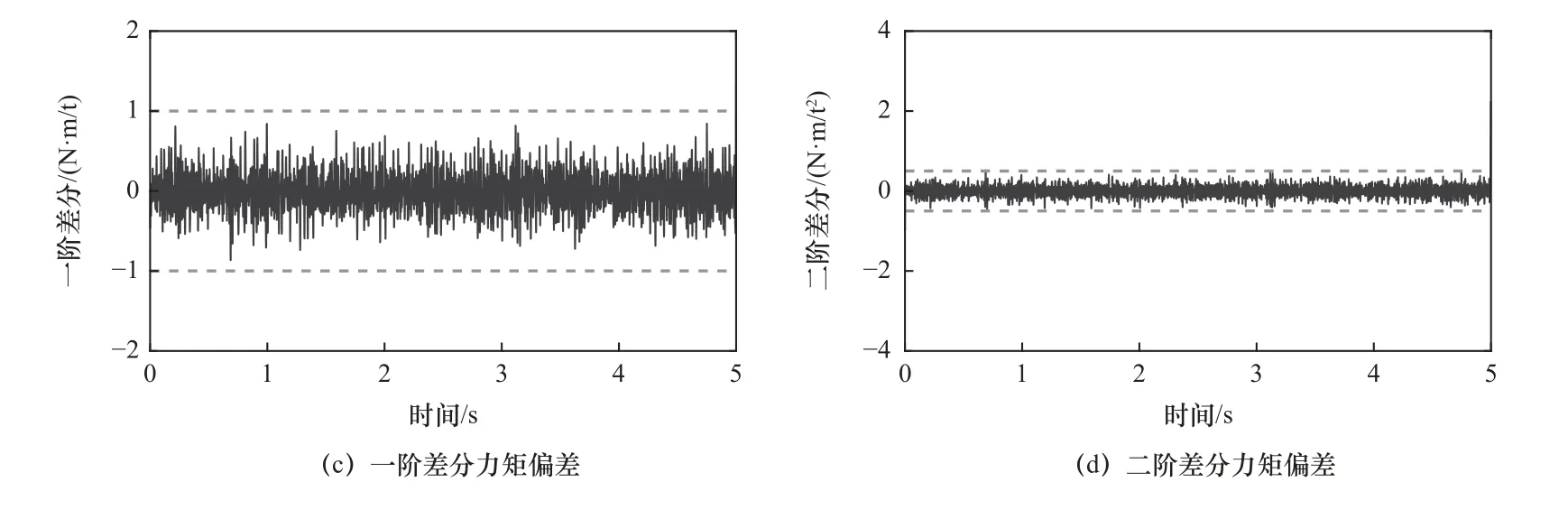
图10 关节3碰撞检测
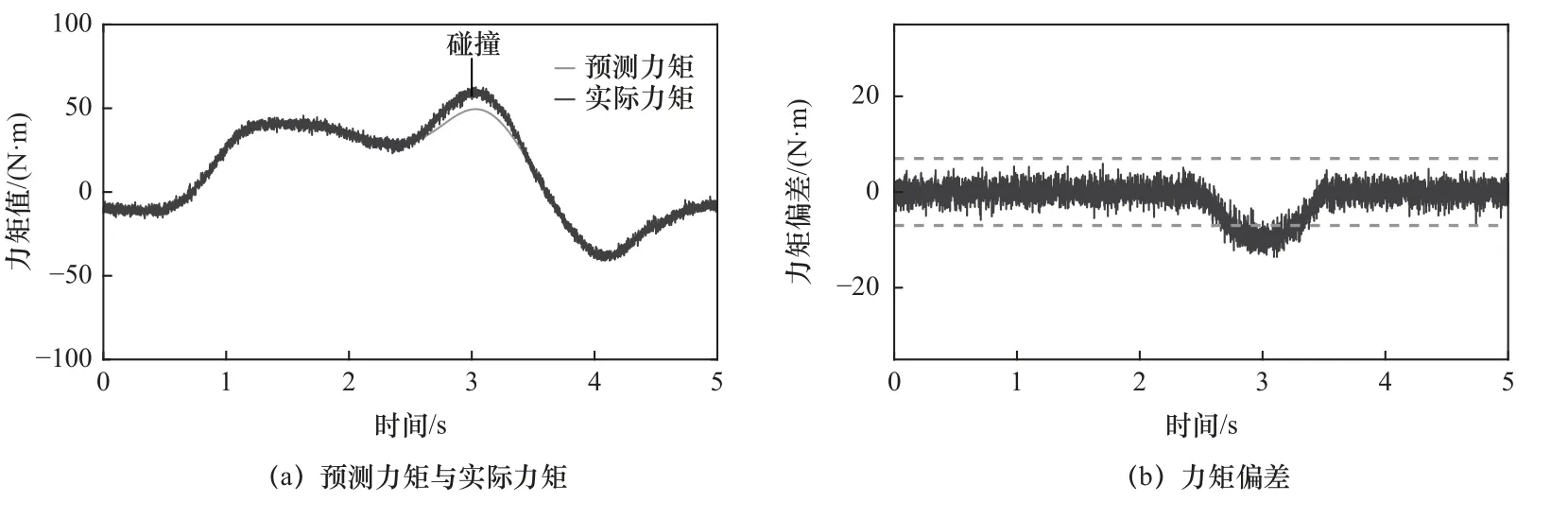
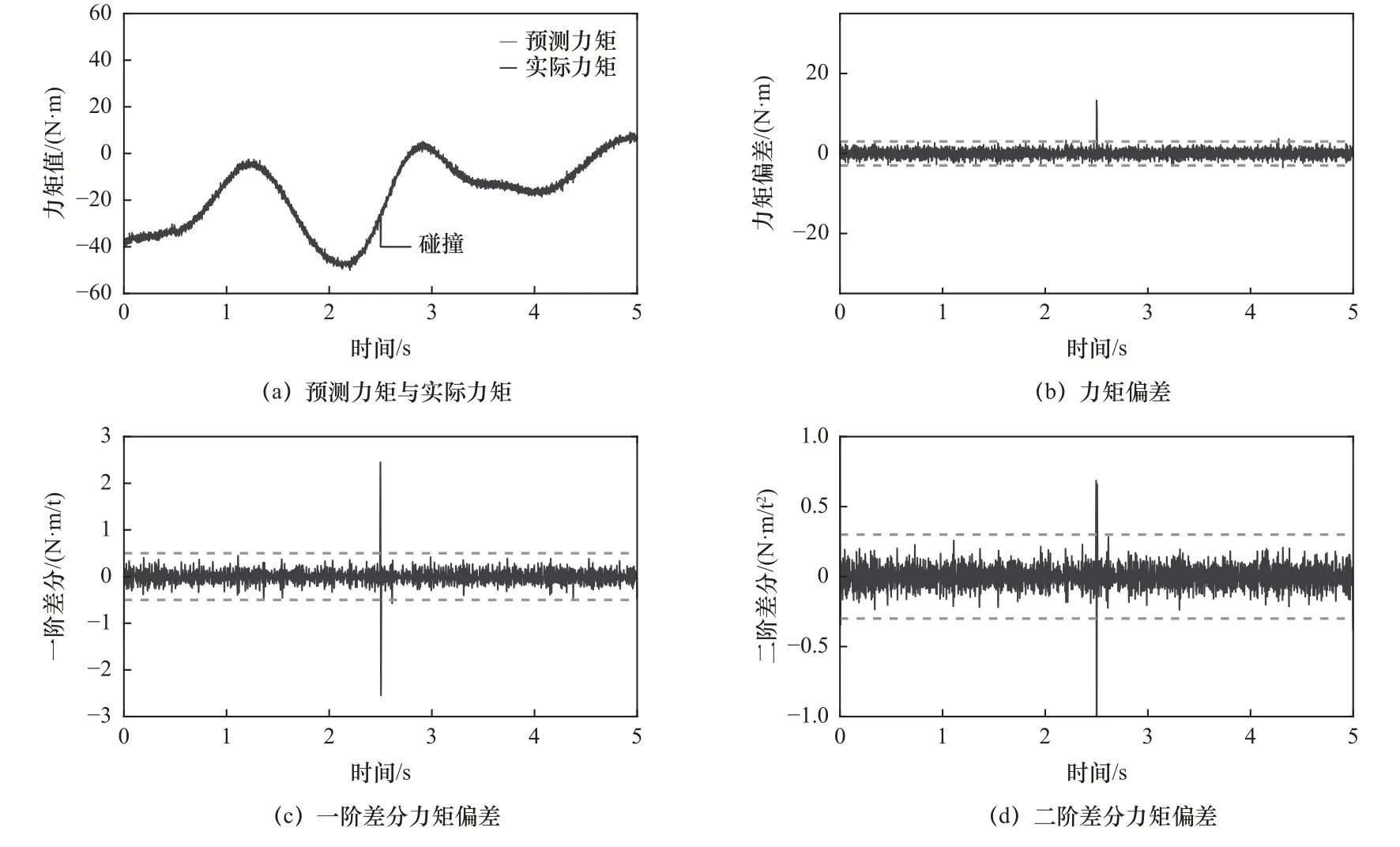
图11 关节4碰撞检测
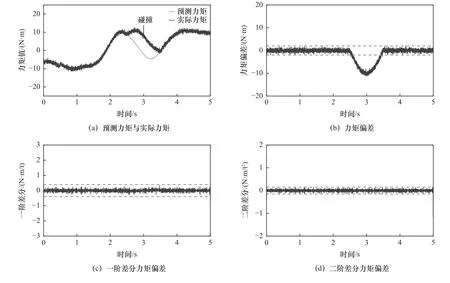
图12 关节5碰撞检测
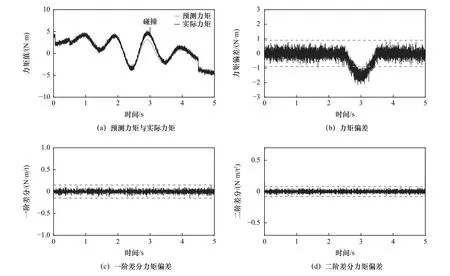
图13 关节6碰撞检测
6 结语
本文提出一种基于机器人动力学模型的差分力矩偏差碰撞检测算法,能够有效检测并将碰撞区分为有意碰撞和无意碰撞,从而使机器人在协同作业时,发生无意碰撞,人为能够将无意碰撞转化为有意碰撞,触发相应的后退机制,避免发生刚性碰撞造成设备损伤,且重新规划路线避免停机造成损失;人为无法干预时触发整机停止机制,避免损伤加剧。与人发生碰撞时,能够有效检测为有意碰撞,从而触发后退机制,避免对人体造成损伤。采用基于惩罚函数的自适应遗传算法优化激励轨迹,在避免算法陷入局部最优解的同时,能够快速获得最优的激励轨迹参数。自适应学习率单层神经网络较加权最小二乘法和递推最小二乘法辨识精度较高,从而使得机器人的动力学参数辨识得更为准确,提高了碰撞检测算法中预测力矩的准确性。实验结果表明,所设计算法能够有效进行碰撞的检测与区分,满足实际生产的需要。
