以应变能最小为目标的航空薄壁件装夹优化方法*
2023-03-10门星臣王仲奇杜兆才常正平
门星臣 王仲奇 杜兆才 李 超 常正平
(①西北工业大学机电学院,陕西 西安 710072;②中国航空制造技术研究院,北京 100012)
薄壁件指各种薄板及加强筋构成的轻量化结构,壁厚小、重量轻且强度高。在航空领域,飞机各类结构件普遍采用薄型板件和加强构件组成的结构。但薄壁件刚性差,且易变形,在装配过程中易产生偏差,影响飞机外形准确度[1]。在薄壁件装配过程中,柔性夹具的布局及夹紧顺序都会对装夹变形有较大影响[2]。因此合理的装夹方案可有效降低薄壁件变形程度,减小最终装配误差。
针对装夹优化问题,国内外学者进行了大量的研究。Cai W等提出了“N-2-1”定位原则[3],并证明出该原理更适用于薄壁件的装夹布局。Padmanaban K P[4]通过蚁群算法优化夹具布局减少工件的装夹变形。Cheng H[5]等人建立了分级优化模型,结合遗传算法与蚁群算法对夹具位置进行了优化。Vasundara M[6]等人以最小化工件的弹性变形为目标,分别使用了人工神经网络(ANN) 和响应面法(RSM)对夹具位置进行优化,结果显示相较于响应面法,人工神经网络成本更低。Selvakumar S[7]等应用人工神经网络建立了装夹变形预测模型,通过优化夹具布局降低工件的最大弹性变形。Kang Y[8]等研究了夹紧顺序模型,并提出了稳定性指标概念。Yang B[9]等利用布谷鸟搜索算法对薄壁件夹具布局进行优化。陈蔚芳[10]等以工件变形最小化和变形最均匀化为目标,应用遗传算法和有限元分析相结合对夹具布局及夹紧力大小进行优化。王仲奇[11]以自重条件下工件的最大变形量最小为目标函数,采用萤火虫算法对夹具布局进行迭代寻优。李诚[12]基于Kriging代理模型与花授粉算法对薄壁件夹具定位布局进行优化设计。杨元[13]等人基于“N-2-1”定位原理,构建了基于支持向量回归机的优化预测模型。许晓宇[14]将遗传算法和有限元方法相结合,对夹紧顺序、夹具布局和夹紧力进行同步优化。秦国华[15]等利用神经网络建立了夹具位置与最大变形间的预测模型,以最大变形最小为优化目标进行求解。董辉跃等[16]采用有限元分析方法,分别对装夹位置、装夹顺序以及加载方式3个因素在装夹过程中对框类薄壁零件产生变形的影响进行了模拟。李国栋[17]提出了基于遗传算法的夹具布局与夹紧顺序同步优化方法,保证了工件的稳定性,提高了加工精度。
现有研究多以最大变形最小化或平均变形最小化作为优化目标,但对于曲面薄壁件,其装配变形存在于多个方向,并非仅集中于某一方向,且忽略了不同区域装夹应力的分布情况。相较于变形量,整体应变能可以更准确反映出薄壁件变形程度及应力分布情况,本文提出以整体应变能作为模型优化目标。在定位元件布局优化的基础上,建立装夹顺序、夹紧元件位置与整体应变能间的非线性映射模型并利用遗传算法进行求解,将优化后夹具坐标代入有限元模型中验证,验证所提方法的有效性,利于实现薄壁件装夹方案的优化。
1 以应变能最小为目标的装夹优化模型
对于弱刚性薄壁件,一般采用“N-2-1”定位原理。该原理认为薄壁件在主定位面上需要N(N>3)个定位点,第二基准面和第三基准面分别需要2个和1个定位点。在主定位面上,随着N值优化越大工件变形越小,这并不代表N值越大越好。随着夹具数量增加,夹具制造误差对薄壁件装配变形影响也会变大,且会导致装配过程设计周期和成本相应增加。在第二和第三基准面上也不宜设置过多定位点,定位点过多易发生定位干涉或使薄壁件翘曲和弯曲,影响工件质量。因此在满足精度要求的前提下,N值越小越好。在薄壁件变形过程中,首先假设弹性体变形是绝热的,即在变形过程中没有热量得失。再假设弹性体在受力变形过程中保持平衡,也没有动能的改变。在弹性范围内外力所做的功W,全部转变为储存于弹性体内的应变能U,即W=U。
将应力与应变写成向量形式:
薄壁件整体应变能简写为
将ui表示单个有限单元的应变能:
薄壁件整体应变能表示为
应力方差公式表示为
式中:σij(i,j=x,y,z) 和 εij(i,j=x,y,z)分别为应力分量和应变分量;U为薄壁件整体应变能;V为薄壁件总体积;ui为单个有限单元的应变能;E为弹性模量;n为有限元模型中单元个数;s2为有限元模型中应力方差。
由上可知薄壁件应变能越小,应力方差越小,应力分布更均匀,且对于曲面薄壁件,其装夹变形存在于多个方向,因此应变能更适合作为衡量优化程度的目标。本文以应变能表征薄壁件变形程度,将应变能最小化作为优化目标,通过优化夹具位置、夹紧顺序,使工件整体应变能最小。以夹具布局X=[x1,x2,···,xi,···,xj,···,xN]为设计变量,设计变量的可行域集合为 Ω,以薄壁件整体应变能U为目标函数,夹具位置优化数学模型可表述为
式中:xi代表夹具位置;N代表夹具个数;ui表示单个有限单元的应变能;n代表有限元模型中单元个数;U为薄壁件在某种夹具布局下的整体应变能。约束条件为N个夹具位置都在可行域上,且同一布局方案中不能出现夹具位置重合。
2 装夹优化模型求解方法
以元件位置、夹紧顺序为变量,以仿真数据为样本,建立输入、输出间神经网络预测模型,以遗传算法为主程序进行优化,优化步骤如下:
步骤1:样本来源。因拉丁超立方采样的随机性优于随机采样,应用其获取50组主定位面上的夹具位置坐标,在ABAQUS环境中计算夹具在不同坐标下对应的整体应变能。
步骤2:建立BP神经网络预测模型。以夹具坐标为输入,以相应布局下薄壁件整体应变能为输出,根据预测模型构建夹具布局与应变能间的映射关系。应用遗传算法迭代寻优得到整体应变能最小时的夹具位置坐标。
步骤3:在定位布局优化的基础上,建立装夹顺序、装夹位置与整体应变能的预测模型。迭代寻优直至获得全局最优的夹具布局与装夹顺序。
步骤4:将寻优到的夹具布局与装夹顺序进行有限元验证,实现对薄壁件装夹变形的有效预测。基于BP神经网络与遗传算法的优化流程如图1所示。
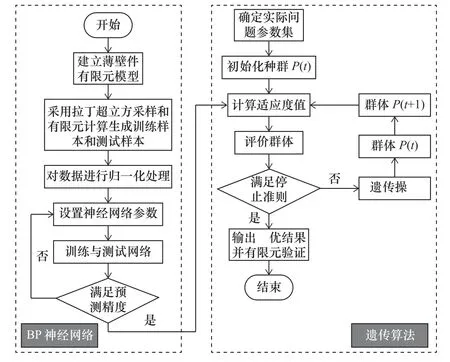
图1 基于BP神经网络与遗传算法的优化流程图
3 基于BP神经网络与遗传算法的定位布局优化
BP神经网络是一种前馈型神经网络,由输入层、隐藏层和输出层3层神经网络组成,每层神经网络都由多个神经元组成,神经元是神经网络的基本处理单元,层与层之间的神经元通过全连接方式相互连接。输入层神经元得到刺激后,会把它传给隐藏层神经元,之后隐藏层神经元会根据神经元之间的权值把这个刺激传给输出层神经元,输出层对比结果,如果不符合要求,则返回修改神经元之间的权值。典型 BP 网络结构示意图如图2所示。
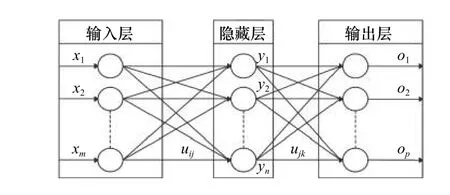
图2 BP网络结构示意图
图2输入层中以xi(i=1,2,3,...,m)表示网络输入,隐藏层中yk(k=1,2,3,...,n)为隐藏层的输出,输出层中oj(j=1,2,3,...,p)为输出层的输出。其中m为输入层节点数目;n为隐藏层节点数目;p为输出层节点数目;uij是输入层与隐藏层间的连接权值;ujk是隐藏层与输出层间的连接权值。
3.1 定位布局与相应应变能的样本生成
在ABAQUS中建立曲面薄壁件,如图3所示,薄壁件长800 mm×宽480 mm×高240 mm,厚度为2 mm,采用“4-2-1”定位原则布置定位点。其中第一基准面上定位点“4”为l1、l2、l3、l4,限制薄壁件的法向位移;第二基准面上定位点“2”为Fl1和Fl2,限制薄壁件的Y向位移;第三基准面上定位点“1”为Fl3,限制薄壁件X向位移。第一基准面上的定位点l1、l2、l3固定,三点坐标分别为:(122.27,206.52,201.46),(122.27,206.52,601.46),(−122.27,206.52,201.46)。第二基准面与第三基准面上定位点Fl1、Fl2、Fl3固定,三点坐标分别为:(−241.97,3.98,300.73),(−241.97,3.98,502.19)和 (1.97,239.95,799.76)。优化l4的位置,使其在自重条件下整体应变能最小。
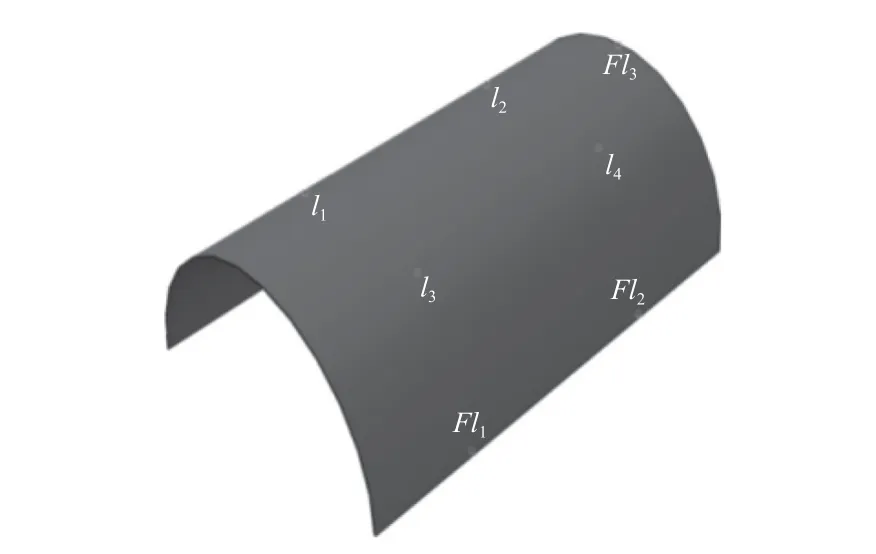
图3 薄壁件几何模型
在薄壁件长边布置150个种子,在圆弧边布置80个种子划分网格。薄壁件材料采用2A12系列硬铝合金,因其强度高、耐热性好,被广泛应用于飞机蒙皮中。采用拉丁超立方采样获取50组第一基准面上的位置,利用有限元分析软件计算获得其相应的薄壁件整体应变能,如表1所示。
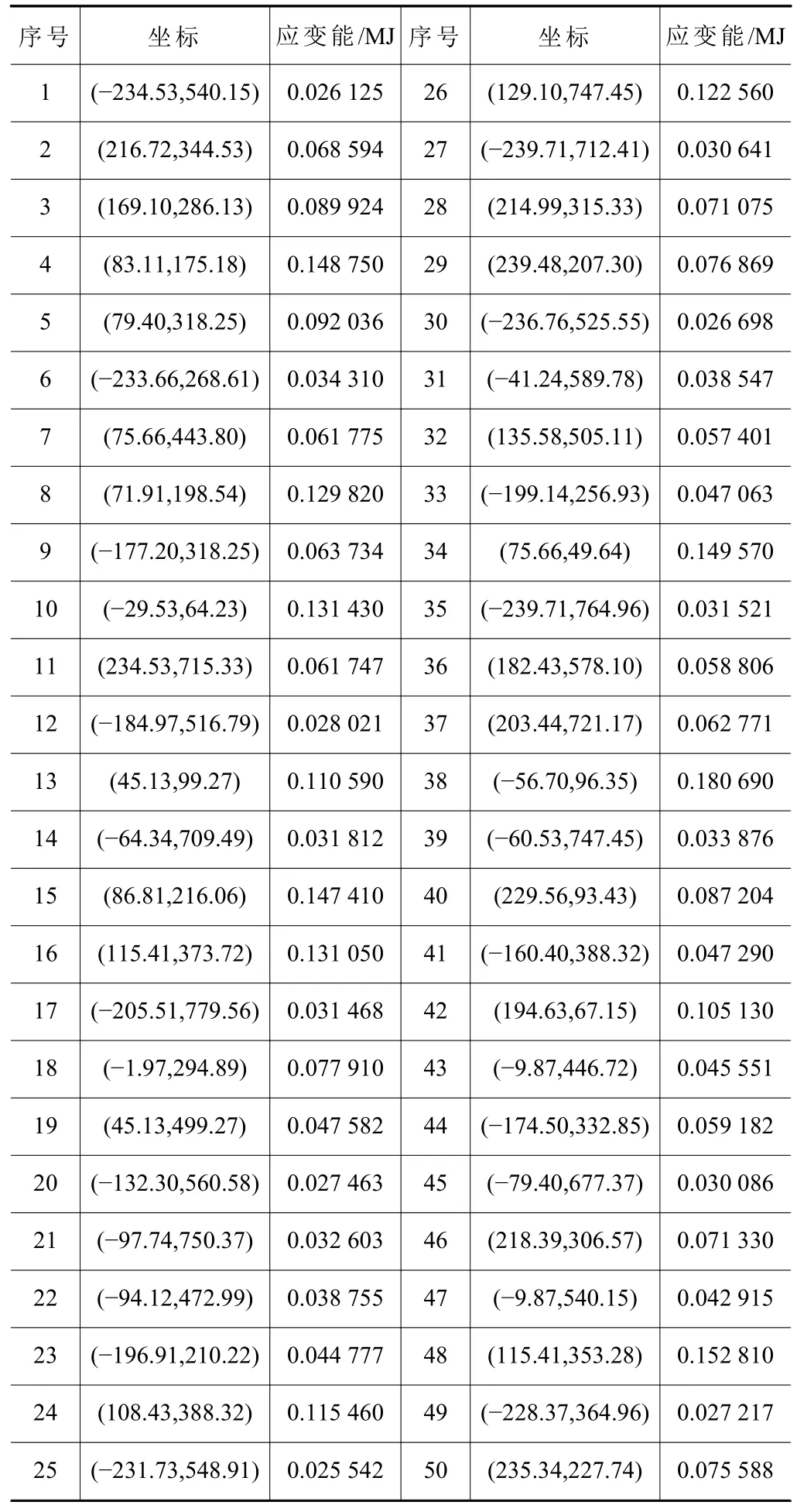
表1 样本数据集
3.2 神经网络训练与验证
采用拉丁超立方采样获取定位元件 l4的50组位置参数作为网络输入样本,利用有限元计算各种位置参数下对应的薄壁件应变能为输出,前40组数据作为网络的训练样本,后10组数据作为网络的测试样本,选定网络学习误差为 1 ×10−3。因神经网络中各输入数据与输出数据物理意义不同,数值大小相差较大,将对其进行归一化处理将各样本数据变换为[0,1]区间的值。归一化处理公式如下:
式中:xi为第i个定位布局参数的输入样本;ximax、ximin为样本的最大值和最小值。
当初始化权系数随机产生后,网络开始训练。根据网络预测,测试样本值与预测结果间误差如图4所示,误差较小训练效果较好。
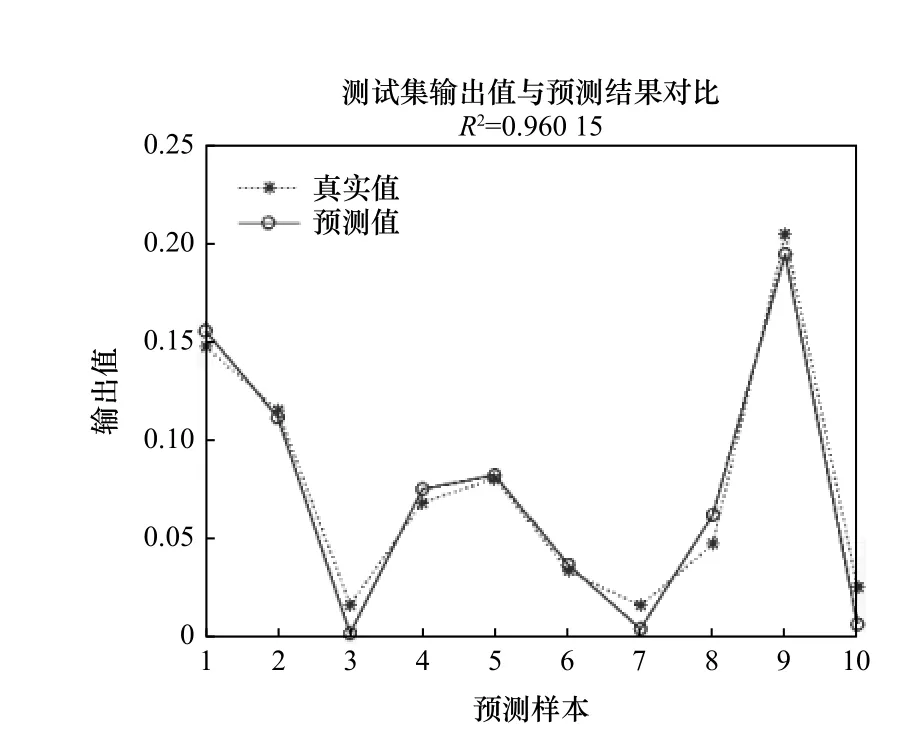
图4 神经网络训练的误差曲线
3.3 基于遗传算法的定位布局优化
遗传算法的基本思想基于达尔文进化论和孟德尔的遗传学说,它是一种模拟生物进化机制的全局搜索最优解的优化方法。遗传算法实施过程中,首先确定优化问题的求解域,在求解域中随机建立由字符串组成的初始化种群,其次利用适应度函数计算种群中个体的适应度。若不满足要求,则对这一代种群进行复制、交换和突变,从而生成新一代种群。如此不断进化,直到获得问题的最优解。利用遗传算法(各参数为个体数目n=50,交叉概率PC=70%,变异概率PM=5%,最大遗传代数m=200)对定位元件 l4位置进行优化,优化过程如图5所示。经过40次迭代,遗传算法达到收敛,薄壁件整体应变能达到最小值0.024 426 MJ,对应x=−224.55 mm、z=508.20 mm。
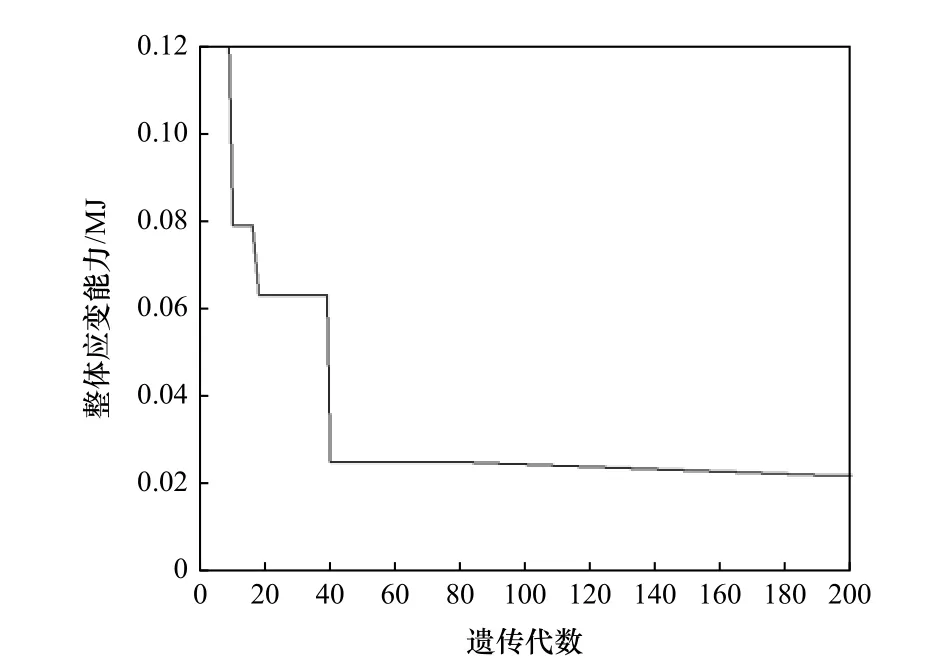
图5 定位元件位置优化过程
为验证以应变能做优化目标的有效性,与最大变形量最小为目标的优化结果进行对比,优化算法参数一致,优化后的结果云图如图6、7所示。输出薄壁件上每个结点应力值,通过方差计算,判断薄壁件应力分布情况。方差越小表示薄壁件应力分布更加均匀,对比两种结果发现,相较于考虑最大变形量的夹具位置优化,以应变能为目标优化的结点应力方差减小了约60%,验证了本文所提方法的有效。

图6 以应变能为目标的优化结果应力云图

图7 以最大变形量为目标的优化结果应力云图
4 基于BP神经网络与遗传算法的装夹方案优化
在薄壁件装配过程中,定位与夹紧是相互联系的,工件在实现定位后,将在后续加工过程中受到自身重力、制孔和铆接等力的作用。为保证工件的稳定性,在定位布局优化的基础上,本节将对夹紧布局与夹紧顺序进行优化,确保薄壁件的位置精度,提高加工质量。
4.1 接触旋量分析
薄壁件在装夹过程中,不仅受其自身重力,还有夹具的夹紧力,施加合适的夹紧力可以保证薄壁件的稳定。但如果夹紧力过大,会使工件内应力集中产生变形,影响装配精度。建立工件稳定性分析模型,保证工件加工过程中的稳定性。装夹时薄壁件受到的外力旋量包括重力旋量Wg和加工力旋量Wm,假设工件某点的夹紧力Fi(t)=Fin+Fit+Fib,其中Fin、Fit、Fib分别代表夹紧力Fi(t)在法向ni、切向ti与bi上的3个分量。Fi(t)对薄壁件产生的接触力旋量可表示为
其中:rCi为夹具接触点位置的单位法向量,Gi为夹持元件的布局矩阵。
要使工件在重力、夹紧力等作用力下保持静态
平衡状态,则其应满足如下静力平衡方程。
其中:G(1)、F(1)分别表示工件 上夹具位置矩阵及接触力向量,Wg为工件重力旋量。
如图8所示,工件重力Fg=[0,−32,0]T,质心坐标为 [242,153,400]T。在上述内容中已根据“N-2-1”定位原则优化确定了定位元件具体位置,按照经验初始确定夹紧元件位置C1、C2、C3,其坐标及法向量如表2所示,夹紧元件与工件间法向力FN=20N。

图8 夹具元件分布图
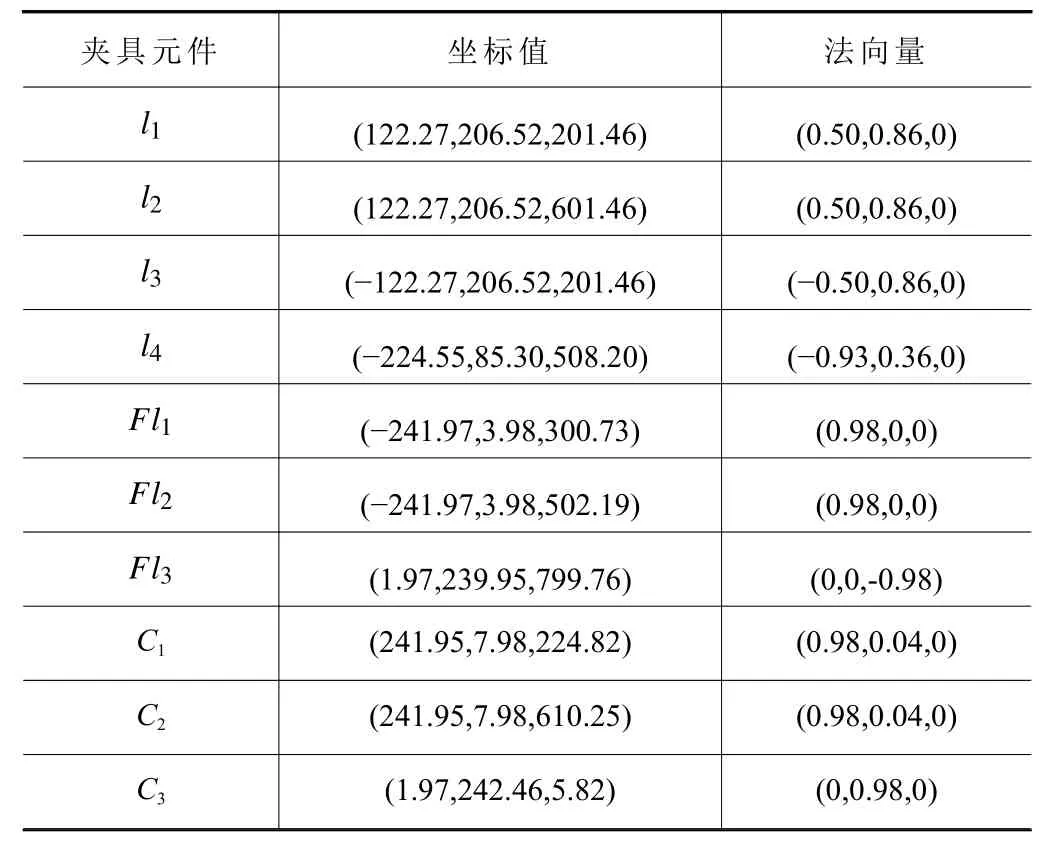
表2 夹具元件位置与方向
求得此时重力旋量:
利用linprog函数进行求解,可知在薄壁件定位夹紧过程中,恒成立,因此薄壁件处于稳定状态。
4.2 装夹方案与相应应变能的样本生成
不同的夹紧元件布局对应的夹紧误差不同,导致工件发生不同程度的位置偏移,影响加工精度;不同的夹紧顺序会产生不同的摩擦力与运动约束,引起不同的接触变形、定位元件变形和工件变形。对夹具布局与夹紧顺序进行优化,可减小上述误差,提高工件加工质量。C2及C3夹紧件位置固定,对夹紧件C1位置进行优化,在区域内抽取10组位置,表3列举了夹紧件C1、C2与C3组成的7种夹紧顺序,表4展示了各装夹顺序下不同夹紧元件位置及相应的整体应变能。
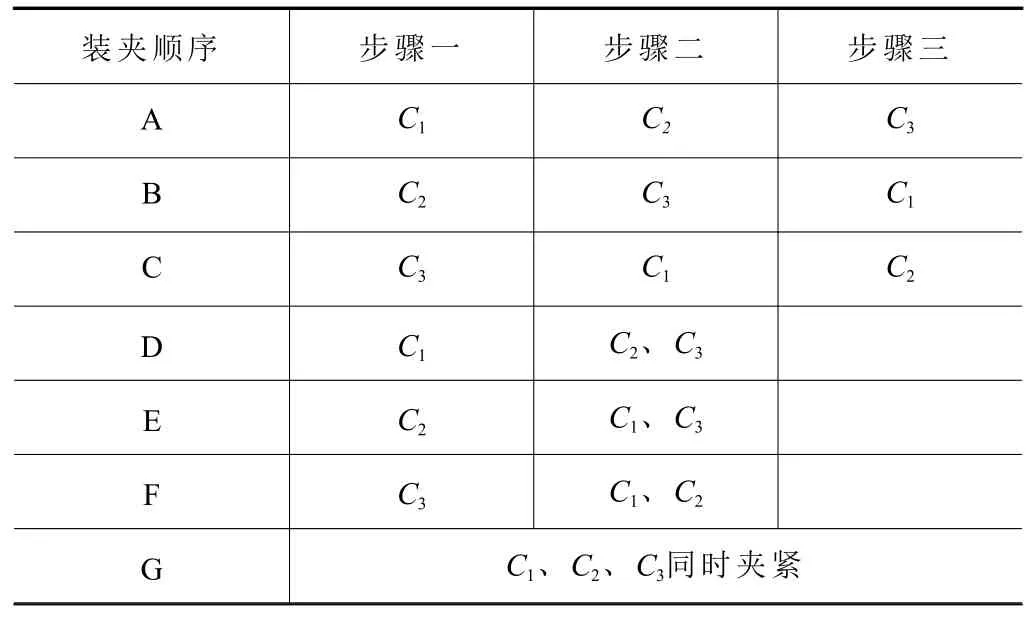
表3 装夹顺序方案
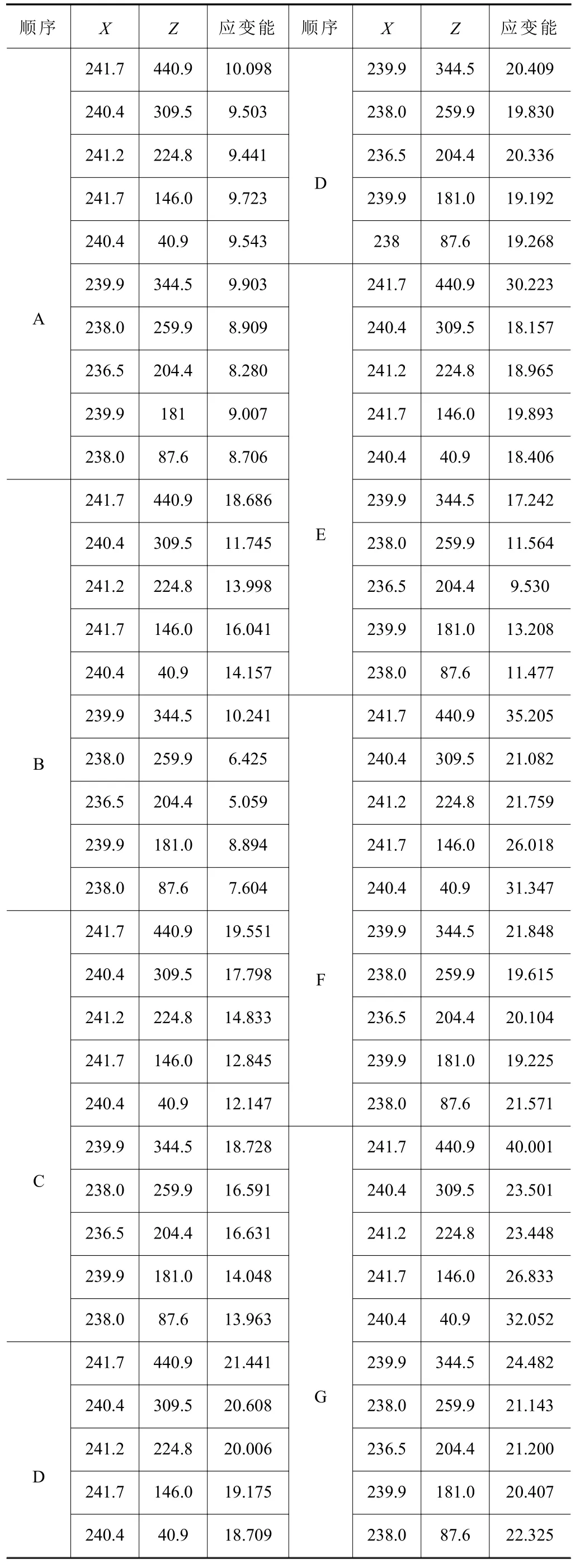
表4 有限元分析结果
4.3 神经网络预测与装夹方案优化
本节神经网络结构为:在给定夹紧力及装夹顺序方案下,研究夹具布局与整体应变能间映射关系。以夹紧元件位置坐标X、Z为输入层神经元,以薄壁件整体应变能为输出层神经元,按照经验公式(12)可确定隐藏层神经元数目m=5。输入层与隐藏层的激活函数选为tansig函数,即隐藏层与输出层的激活函数选为logsig函数,即
式中:l代表输入层神经元个数。
对7种顺序下各网络进行预测,发现测试样本值与预测结果间误差均在5%以内,证明BP神经网络是有效的。利用遗传算法(各参数为个体数目n=30,交叉概率PC=70%,变异概率PM=5%,最大遗传代数m=200)对顺序A下夹紧件C1位置进行优化,迭代过程如图9所示,横坐标为遗传代数,纵坐标为目标函数。由图可知随着迭代次数的增加,薄壁件整体应变能不断减小,在迭代45次以后,薄壁件应变能取得最小值3.631 MJ,此时C1位置为X=230.3 mm、Z=260.0 mm。优化剩余六种夹紧顺序下夹紧件位置,通过对比优化结果发现最优夹紧顺序为方案B,夹紧件位置为X=223.4 mm、Z=242.3 mm时,薄壁件整体应变能取最小值2.662 MJ。将优化后的C1位置代入有限元模型中验证,发现误差在5%以内,将其与最大变形量最小为目标函数的优化结果进行对比(优化结果为夹紧顺序为方案B,夹紧件位置为X=232.7 mm、Z=213.1 mm,Umax=0.32 mm),以输出结点应力方差值表征应力分布均匀程度,发现以应变能为目标优化的结果应力方差值减小了约64%,应力分布均匀程度远高于后者,因此通过遗传算法优化夹紧位置及夹紧顺序的方法是有效的。
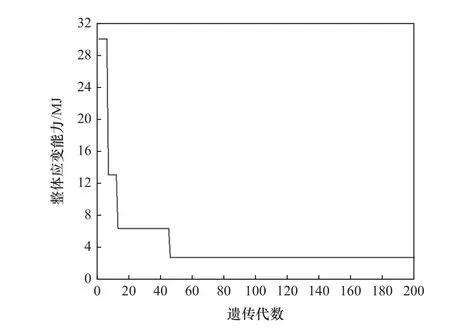
图9 夹紧元件位置优化过程
5 结语
为实现航空薄壁件装夹方案优化,本文建立了以装夹位置为决策变量,以最小化整体应变能为目标的布局优化模型,并提出一种结合神经网络和遗传算法的参数化有限元分析来实现薄壁件装夹优化的方法。主要结论包括:
(1)应变能可反映薄壁件所有方向上的变形程度及装夹应力分布情况,通过对比以最大变形量为目标的优化结果,以应变能为目标优化的结点应力方差减小了约60%,因此应变能更适合作为曲面薄壁件优化模型的目标函数。
(2)以薄壁件整体应变能最小化为优化目标,对定位、夹紧两阶段参数进行优化,得到最优装夹顺序及夹具位置,有效控制了薄壁件的装夹变形大小与应力分布情况。
