ANP 耦合博弈论的煤矿安全评价研究

李月强，赵琳琳

煤矿生产系统是一个容易发生突发事故的复杂多变系统，该系统的生产环节多，各种影响指标在时空上交叉作用，导致煤矿事故的影响范围广、损失较严重，为此迫切需要做好煤矿安全预评价，以确保矿井生产的安全进行。目前国内外学者及相关领域专家采用相关理论对煤矿安全预评价方法进行了相关研究，如事故树分析法［1］、神经网络方法［2-3］、集对分析［4］、层次分析法［5-6］等。上述方法已取得了较好的成果，但这些方法基本上是构建多指标的单个或多个模型对样本进行评价，未考虑影响指标的交叉作用，评价结果的准确性和可靠性不强。网络分析法［7］（Analytic Network Process，ANP）是一种能够刻画众多影响指标之间相互依存与反馈关系，以及各层次间支配关系的方法，但其在有序或无序的网络分析时较难进行评价。博弈论作为一种解决多准则决策问题的理论，已被广泛应用到决策领域，如合同能源管理、公路项目管理、供应链协调、零售商产品回收决策、产品投资决策等。

一、网络分析法及双矩阵博弈模型

1..网络分析法

ANP 是由萨帝（T.L.Saaty）教授在2001 年首次提出的，是一种基于层次分析的多准则、多目标系统决策方法。该方法将系统分为控制层和网络层两部分。

ANP 数学模型为：

设控制层的准则集为B={B1，B2，…，Bm}，网络层的指标集为C={C1，C2，…，Cn}，设第i个样本集Ci有li个指标组成，记为Ci={di1，di2，…，dili}，第j个样本集Cj有lj个指标组成，记为Cj={dj1，dj2，…，djlj}，以Bs为准则，Ci中指标dji为次准则。若以Ci中指标对Cj中指标dji的重要程度进行间接优势度比较，可构造归一化特征向量（s为Cj中指标个数），若将这些向量组成一个新的矩阵，则可构造超矩阵W=(Wij)n×n。由此，按Ci中指标对Cj的重要性进行比较，得到归一化排序向量Aj=[a1j，a2j，…，anj]T，则加权超矩阵=A∗W，其中A=[A1，A2，…，An]T。为获得更稳定结果，求W的K次幂极限值，所得结果非零相同值为网络指标的权重。

2.双矩阵博弈模型

设某方案优选问题，其方案集为S=(s1，s2，…，sn)，属性集为P=(p1，p2，…，pm)，方案sj下属性pi的属性值为xij，由此构成的决策矩阵为X=(xij)m×n，将X作为决策者的支付矩阵，-X为自然支付矩阵， 决策者混合策略矩阵为自然混合决策矩阵为记为Γ={DM，Nature，SD，SN，X}。

经典双矩阵博弈求解中，若一对数组(x*，y*)∈(SD，SN)是博弈Γ 的一个满足 “≤” 关系的均纳什均衡，有：

则称x*TSD y*，x*TSN y*为Γ 中决策者和自然人的值，(x*，y*)∈(SD，SN)是Γ 的纳什均衡解。由此，可通过构建对偶线性规划模型得到最优解(x*，y*)。

二、ANP-博弈模型

根据国家及领域特点，结合有关假说，在保证科学性、可操作性等原则基础上，本研究选取有关指标，并结合相关规定及实际的工程情况，对指标各安全情况下临界值进行确定。

1.指标间关系及与等级关系确定

本研究利用网络结构表示已确定的指标体系各层次指标间的关系，采用1～9 位标度法、层次分析法或德尔菲法等对各准则层指标以及不同准则下指标进行两两比较，得到第m，n准则层间判断矩阵Rmn，以及Ci下指标两两判断矩阵RCi ij，利用特征向量法进行归一化处理，则可获得未加权超矩阵，以此得到指标对各级别影响rdij。

2.安全预警级别判据

根据矿井安全生产特点和国家安全生产相关部门的规定，以及影响指标的数值将矿井安全状态分为5 个级别：V=｛V1，V2，V3，V4，V5｝=｛“安全”，“较安全”，“中等安全”，“较不安全”，“不安全”｝，安全状态级别评价标准借鉴了贾宝山等人的研究。

3.综合结果评判

基于决策矩阵A=(aij)m×n及指标对各级别影响rdij，可定义待评样本综合评价预得分为：

式中：S'D=rdijSD，(x*，y*)∈(SD，SN)。

三、实例应用

1.安全评价指标及层次结构

科学、合理的指标体系对矿井安全状态评价至关重要。本研究基于事故致因理论，从人、物、环境和管理等方面分析矿井安全现状，结合层次分析法基本原理，建立矿井安全状态指标体系。

（1）人的因素（B1）：人员三违率（d11），月平均培训时间（d12），平均工龄（d13）。

d11，d12，d13存在相互依赖性。d11低，未必d12长d13小；d12长一定d11低，未必d13小；d13小未必保证d11低d12短。

（2）物的因素（B2）：提升设备完好率（d21），运输设备完好率（d22），机电设备完好率（d23），通风设备完好率（d24），排水设备完好率（d25），防灭火设备完好率（d26）。

（3）环境因素（B3）：煤层倾角（d31），矿井正常涌水量（d32），煤层最短自燃发火期（d33），顶底板可靠率（d34），工作面粉尘最大浓度（d35），万吨煤瓦斯异常涌出次数（d36）。

d31与d22是相矛盾的。d31越小，d22越高，反之亦然；同理，d32与d25，d35与d24均相矛盾；d33与d26，d36与d24，相互之间具有一定的依赖性。

（4）管理因素（B4）：安全制度完善率（d41），安全措施完善率（d42），安全管理有效率（d43），安全管理时效率（d44），应急机制完善率（d45）。

B2中各指标与B1和B4中各指标是依存的，如d11越低，d41越高，则d21一定越高，以此影响矿井安全状态。

2.指标的依存和反馈关系

根据已建立的指标体系关系，为进一步明晰同一准则和不同准则的指标间相互关联（依存或反馈）关系，本研究根据领域专家的知识获得指标间的关联情况（见表1）。

表1 指标关联

续表

根据表1 指标关联情况，利用SuperDecisions 软件构建控制层元素和网络层的ANP 结构图，如图1。

图1 ANP 结构

依据表1 指标关联情况，为获得指标相对重要程度，构建B1，B2，B3，B4所影响的下级指标的判断矩阵，即将被影响指标二级指标对应的三级指标中划“√”的三级被影响指标计数，得到二级指标关联的表，如表2。

表2 二级指标关联

由表2 可知，A与B1，B2，B3，B4，B1与B1，B2，B4，B3与B2，B4与B1，B2，B4的计数均大于0，故根据判断矩阵的构造原则，可构建二级指标判断矩阵并结合德尔菲法获得二级指标重要程度，即A影响下B1，B2，B3，B4的权重分别为0.583，0.218，0.126，0.071，B1影响下B1，B2，B4的权重分别为0.773，0.139，0.087，B4影响下B1，B2，B4的权重分别为0.733，0.199，0.067。同理，若三级指标关联计数大于1，可利用构建的两两比较矩阵，结合德尔菲法获得二级指标重要程度如表3。

表3 三级指标重要程度

3.指标权重的ANP 计算

为获得各指标的权重，对已构建的两两判断矩阵进行特征向量法进行归一化处理，本研究利用Super Decisions 软件，获得未加权超矩阵，如表4 所示。

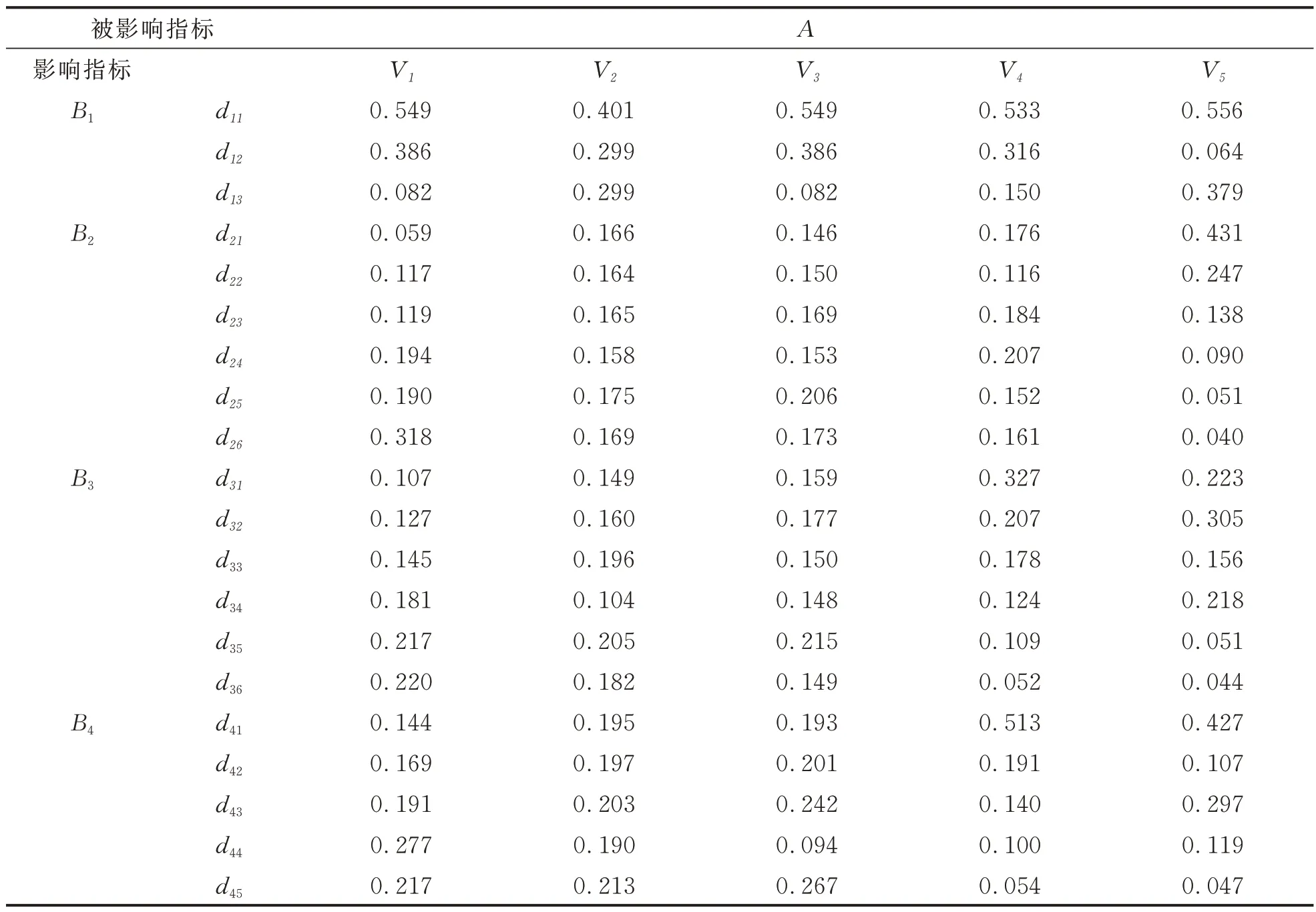
表4 未加权超矩阵

由4 可知，d11对各等级影响较明显，d12和d26对V1，V2，V3和V4影响较明显，d23和d33对各等级影响相差不多，影响V1较明显的指标为d11，d12和d26，较不明显的指标为d13和d21，影响V2较明显的指标为d11，d12和d13，不明显的指标为d34，影响V3较明显的指标为d11和d12，较不明显的指标为d13和d44，影响V4较明显的指标为d11，d12，d31和d41，较不明显的指标为d36和d45，影响V5较明显的指标为d11，d13，d21，d32和d41，较不明显的指标为d25，d26，d35，d36和d45。

4.安全状态综合评价

利用表4 权重信息及文献［5］给出的评价标准，构建加权双矩阵博弈模型，并利用对偶线性规划模型， 求解得：x*=（0.5800982，0.2990324，0.1073445，0.1837567，0.4098665），y*=（0，0，0，0.4839052，0，0.1460908，0，0，0.1223217，0，0，0，0，0，0，0，0，0，0.15414893，0）。为此利用式（3）求得方案V1，V2，V3，V4的得分分别为7.178696696，4.485264261，2.507447314，2.352576605，待评样本得分为6.846059007。可知该样本级别为V2，结果与文献［5］相同，但求解过程相对比较简捷，且考虑了指标间关联性。

四、结论

采用ANP 和博弈论对煤矿安全状况评价时，需要综合考虑人、物、环境和管理等方面的因素。本研究构建了煤矿安全评价指标AHP 分析结构及安全状况双矩阵博弈模型，并进行了实例分析。结果表明，该模型优选结果与ANP 耦合TOPSIS 的结果均一致，求解过程简捷，无须对指标重要性赋权，避免类似ANP 优选法因人为赋权而带来的结果差异性现象。