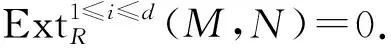Cohen-Macaulay局部环上的Canonical模

路姣姣, 杨晓燕

(西北师范大学 数学与统计学院, 兰州 730070)

0 引 言

设(R,m,k)是Cohen-Macaulay局部环,M是有限生成R-模.对Cohen-Macaulay局部环上的canonical模, 目前已有很多研究结果： 文献[1]详细介绍了Cohen-Macaulay模、极大Cohen-Macaulay模以及Cohen-Macaulay环上的canonical模, 并给出了canonical模的等价刻画; 文献[2]定义了两个子范畴ΩDeep(R)和DF(R), 并讨论了这两个子范畴中有限生成模的性质, 尤其是子范畴ΩDeep(R)中的模与自由模的充分条件; 文献[3]证明了canonical模ω的内射维数有限等价于ω的投射维数有限.由canonical模和Gorenstein环的定义可知, Gorenstein环上的canonical模是R本身.文献[4]给出了存在canonical模的Cohen-Macaulay环是Gorenstein环的条件; 文献[5-6]对Cohen-Macaulay环成为Gorenstein环进行了进一步研究.本文主要研究在Cohen-Macaulay局部环上有限生成模的一些性质.

1 预备知识

设(R,m,k)是诺特局部环,M是有限生成R-模.SuppM={p∈SpecR|Mp≠0}称为M的支撑, dimM=sup{r|存在长度为r的链, 即p0…pr, 其中pi∈SuppM}表示模M的维数, 当R本身作为模时, SpecR=SuppR, dimR表示环R的维数, 其中SpecR表示R的素理想的集合.depth称为M的深度.因为M是有限生成R-模, 所以depthM也等于极大理想m中M-正则序列的最大长度.对于元素x∈R, 如果xy=0,y∈M⟹y=0, 则称x是M-正则的, 若xi是M/(x1,x2,…,xi-1)M-正则的(i=1,2,…,n), 并且则称序列是M-正则序列.pdM表示模M的投射维数.若M≅M**, 则称M是自反模[7], 其中M**=HomR(HomR(M,R),R).

设M是有限生成R-模.如果depthM=dimM, 则称M是Cohen-Macaulay模, 如果depthR=dimR, 则称(R,m,k)是Cohen-Macaulay局部环.CM(R)表示Cohen-Macaulay局部环上由极大Cohen-Macaulay模构成的模类, 即

M∈CM(R)⟺dimM=dimR(或者depthM=depthR).

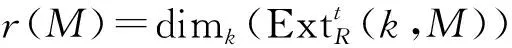
ΩCM(R)={M|0→M→Rn→XM→0,n∈,XM∈CM(R)},

DCM(R)={M|0→R→Mn→XM→0,n∈,XM∈CM(R)}.

如果R是Gorenstein环, 则每个canonical模ω∈ΩCM(R)∩DCM(R).

注1由子范畴ΩCM(R)的定义知,ΩCM(R)由CM(R)的合冲组成.故ΩCM(R)⊆CM(R).

引理1CM(R)关于扩张和有限直和封闭.

证明: 设有正合列

0→M′→M→M″→0,

只需证当M′,M″∈CM(R)时,M∈CM(R).因为dimM=sup{dimM′,dimM″}=dimR, 所以M∈CM(R).

引理2设0→M′→M→M″→0是R-模正合列.若M∈ΩCM(R)且M″∈CM(R), 则M′∈ΩCM(R).

证明: 因为M∈ΩCM(R), 所以有正合列

0→M→Rn→XM→0,

其中XM∈CM(R),n∈.考虑如下推出图:

因为XM,M″∈CM(R), 所以由引理1知P∈CM(R).故M′∈ΩCM(R).

引理3设0→M′→M→M″→0是R-模正合列.若M′∈DCM(R)且M″∈CM(R), 则M∈DCM(R).

证明: 因为M′∈DCM(R), 所以有正合列

0→R→M′n→XM→0,

其中XM∈CM(R),n∈.考虑如下推出图:

因为XM,M″∈CM(R), 所以由引理1知M″n∈CM(R), 从而P∈CM(R).故M∈DCM(R).

证明: 因为M∈ΩCM(R), 所以有正合列

0→M→Rn→XM→0,XM∈CM(R).

(1)

用HomR(-,R)作用正合列(1)，得

(2)

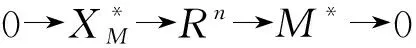
从而有如下正合列：

因为XM是自反模, 所以有交换图:

故M是自反模.

2 ΩCM(R)中有限生成模是canonical模的条件

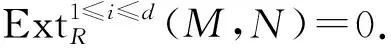
证明: 取M的极小自由分解

F: 0→Kd→Fd-1→…→F2→F1→M→0.

因为R是Cohen-Macaulay环,M是有限生成R-模, 所以由文献[1]中习题2.1.26知, 在M的自由分解中,M的第d个合冲或者是0, 或者是极大Cohen-Macaulay模.当Kd=0时,M的极小自由分解为:

F: 0→Fd-1→…→F2→F1→M→0.

(3)

0→HomR(M,N)→HomR(F1,N)→HomR(F2,N)→…→HomR(Fd-1,N)→0.

记HomR(Fi,N)=Nni(i=0,1,…,d), 则有正合列:

0→HomR(M,N)→Nn1→Nn2→…→Nnd-1→0.

(4)

由正合列(4)可得下述两个正合列:

0→HomR(M,N)→Nn1→K→0,

0→K→Nn2→Nn3→…→Nnd-1→0.

因为N∈ΩCM(R)⊆CM(R), 并且CM(R)关于有限直和封闭, 所以Nni∈ΩCM(R)⊆CM(R).故K∈CM(R).当Kd≠0时,M的极小自由分解为

F: 0→Kd→Fd-1→…→F2→F1→M→0.

0→HomR(M,N)→HomR(F1,N)→HomR(F2,N)→…→HomR(Fd-1,N)→HomR(Kd,N)→0.

记HomR(Fi,N)=Nni(i=0,1,…,d), 则有正合列:

0→HomR(M,N)→Nn1→Nn2→…→Nnd-1→HomR(Kd,N)→0.

(5)

由正合列(5)可得下述两个正合列:

0→HomR(M,N)→Nn1→K→0,

0→K→Nn2→Nn3→…→Nnd-1→HomR(Kd,N)→0.

因为Kd是R上的极大Cohen-Macaulay模, 并且N是有限生成Cohen-MacaulayR-模, 所以由文献[1]中命题3.3.3知, HomR(Kd,N)是R上的极大Cohen-Macaulay模, 即HomR(Kd,N)∈CM(R), 所以K∈CM(R).由引理2知, HomR(M,N)∈ΩCM(R).

推论1设(R,m,k)是Cohen-Macaulay局部环,M∈ΩCM(R)是有限生成模.若canonical模ω∈ΩCM(R), 则HomR(M,ω)∈ΩCM(R).

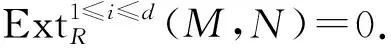
证明: 结合定理1和引理3可证, 故略.

νd(HomR(M,ω))=μ(M)νd(ω)=μ(M)νd(N).

所以IdRN≤d-1, 并且νd(N)=νd(ω)=1, 因此N是R上的canonical模.

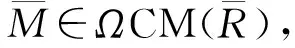
证明: 因为M∈ΩCM(R), 所以有正合列

0→M→Rn→XM→0,XM∈CM(R).

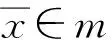
于是0→M/(x1M)→Rn/(x1Rn)→XM/(x1XM)→0正合, 又由depthXM/(x1XM)=depthXM-1, depthR/(x1R)=depthR-1, 且depthXM=depthR, 所以depthXM/(x1XM)=depthR/(x1R), 从而XM/(x1XM)∈CM(R/(x1R)), 进而M/(x1M)∈ΩCM(R/(x1R)).同理有正合列