级联随机共振线谱检测粒子群优化算法

曹泽超，韩 鹏，陈思瑜，白园园

(西北工业大学航海学院，陕西 西安 710072)

0 引言

由于水中声场作用距离远，其成为目前水下探测最常应用的水下物理场之一。大量研究表明，通过对水下目标辐射噪声的线谱来提取相应特征是分析水下目标工作特性最有效的方式之一[1-12]。随着降噪技术的提高以及复杂多变的海洋环境噪声的影响，水下目标辐射噪声的信噪比大大降低，如何在复杂且多变的海洋背景噪声环境中实现对敌方水下目标的线谱检测就成为了水声探测领域的难点[13-17]。

在20世纪80年代，为了研究地球冰川期与暖气候期的交替周期问题，Benzi等人第一次提出了随机共振(stochastic resonance，SR)[18-19]，为检测低信噪比线谱信号提供了思路。

虽然在大多数情况下，信号中的噪声总是起着干扰阻碍的作用，人们总是想保留信号频率而滤除不相关的噪声分量。但在某些情况下，噪声也能够被加以利用，并且起到促进信号提取、信号增强、信号检测等作用。随机共振通过在具有非线性势阱的系统中添加合适强度的噪声或者利用混杂在信号中的噪声，使得微弱周期信号在噪声的协助下在势阱之间跃迁，微弱信号的幅值或功率由此得到增强。随机共振系统可以理解为一个非线性的滤波器，不同于传统的抑制噪声频段的线性滤波器，它能够通过调节滤波器系数利用噪声能量来提高输出信号信噪比[20]。

传统的线谱增强方法一般是通过增加功率谱的积分时间来实现的。这种措施在信号为平稳信号时，效果较好；然而，对于非平稳信号，如果分析时间间隔内信号线谱频率发生漂移，采用长的积分时间会导致谱峰展宽，强度和分辨率下降[21]。此外，线谱增强方法还有利用自适应FIR线谱增强器，其中运用的自适应算法有LMS、RLS、APA等[22]。LMS算法简单，易于实现，算法复杂度低，但是算法的收敛速率较慢，在步长与收敛速度、失调之间存在着矛盾[23]，同时，每一次采样点梯度的估计对于真实梯度会存在一定误差，跟踪性能较差。RLS算法的优点是收敛速度快，其收敛性能与输入信号的频谱特性无关，能够对非平稳信号进行跟踪，但其缺点是计算复杂度很高，所需的数据量极大，不利于实时实现[24]。APA算法通过重复利用过去的数据信号来提高收敛速度算法，计算复杂度较高，其性能介于LMS算法和RLS算法之间[25]。自适应FIR线谱增强器的优点在于具有内在的稳定性和易于自适应，但同时也存在着一定的不足[26]。

相较而言，随机共振作为一种典型的非线性系统，可检测信噪比可以达到-20 dB以下[27-28]。同时，随机共振系统不仅具有能够在短数据集条件下应用的特点，而且算法的计算复杂度不高，可以采用硬件电路的方法来求解随机共振[29]，通过电路的硬件化嵌入能够做到随机共振算法的快速、实时解算，只需对随机共振系统的输出信号进行快速傅里叶变换即可得到已增强的信号线谱。因而，自随机共振理论提出以来，在机械系统故障检测[30-32]、生物[33]、电子[34]、神经网络[35]等众多学科领域，取得了较好的效果。在水下信号检测与通信研究领域，国内外学者也开展研究并取得一定进展[36-42]。

为了解决随机共振系统在实际检测低信噪比水下目标信号时，由于目标信号频率未知而难以达到随机共振状态并且检测效果不理想的问题，本文在研究变尺度随机共振方法的基础上，将级联型系统和自适应的思想引入随机共振系统，实验结果证明了该系统在水声探测中应用的优越性和可行性。

1 基本理论

1.1 变尺度随机共振

随机共振系统是一个受到外部激励信号作用的非线性系统。该外部激励信号既可以是周期性正弦信号Acos(ωt)，也可以是无规律的噪声信号Γ(t)。一般用郎之万方程(LE)描述[43](式中a、b分别为线性和非线性项系数)：

(1)

这里将系统吸引子曲线的零点间距称为跃迁宽度L，将系统吸引子曲线的极值点的纵坐标称为跃迁阈值δyq。由系统吸引子曲线方程可以推算得到：

(2)

(3)

由式中可以看出，通过调节郎之万方程中的系统参数a和b便可达到调节系统跃迁阈值和跃迁宽度的效果。

大量研究表明，对于满足绝热近似理论的小参数信号(信号的频率、幅值远小于1)，利用随机共振特性可以实现微弱周期信号的检测。然而实际工程中的水下目标信号频率都是在几十赫兹到几百赫兹量级之间，并不满足小参数信号条件，因此需要进行尺度变化[44]。由于噪声干扰并不影响系统输入和输出信号的周期成分的频率，因此先忽略噪声的作用，得到无噪声干扰的郎之万方程：

(4)

令

t=mξ。

(5)

经过推导变型可得到如下所示的郎之万方程：

(6)

为了解决工程实际问题，设计新的郎之万方程如下：

(7)

这样可以得到解决待检测水下目标信号频率未知时的系统检测方案，即通过不断改变系统的阻尼系数k，进而调整整个随机共振系统，直至得到相应的处于随机共振状态的输出信号为止。此时输出信号的信噪比得到明显提升，通过对线谱幅值设置门限即可提取到相应的线谱信息。

由郎之万方程可知，可分为以下四类可调整系统参数：

1)系统的输入噪声

只能单向地通过增加噪声Γ(t)来调节系统参数，无法灵活调整系统处在随机共振状态，故只在系统特定状态下考虑。

2)系统的阻尼系数

当系统的输入激励信号无法使系统的输出信号处于随机共振状态时，通过调整阻尼系数k便可以达到效果。

3)系统的跃迁阈值

系统的跃迁阈值δyq越小，系统的输入信号中幅值超过跃迁阈值的点就越多，此时系统输出信号越容易出现随机共振现象。

4)系统的跃迁宽度

随机共振系统的跃迁宽度L越宽，系统的随机共振现象越不易出现；反之，系统的随机共振现象越容易出现。

1.2 粒子群优化算法

粒子群优化算法(PSO)是智能计算领域除了蚁群算法、鱼群算法之外的一种群体智能的优化算法。该算法实现方便，与遗传算法相比需要设置的参数少，是一种高效、实用的搜索优化算法[45]。

PSO算法从鸟类觅食模型中得到启示并用于解决优化问题。在PSO算法中，每个优化问题的解决方法就是利用搜索空间中的每一只鸟，这里称之为粒子，所有的粒子都有一个由适应度函数决定的适应度值，同时还有一个速度决定它们飞翔的方向和距离，通过不断调整速度，粒子们就追随当前最优粒子在解空间中搜索。PSO算法初始为一群随机粒子，也就是随机解，然后通过多步迭代找到最优解。在每一次迭代中，粒子通过跟踪两个极值来更新自己，一个极值就是粒子自身所找到的最优解，另一个极值是整个种群目前找到的最优解。算法流程如图1所示。

由于粒子群优化算法在使用时存在一个适应度函数，也就是判定系统达到最优状态的函数。这里本文将随机共振系统的输出信噪比作为算法的适应度函数，通过三维粒子群算法自动寻优找到产生最大输出信噪比的随机共振系统参数a、b、k的值。适应度函数F定义如下：

F(a,b,k)=SNR(SR(a,b,k))，

(8)

式(8)中，SR即随机共振系统模型，SNR为随机共振系统的输出信噪比。

图1 粒子群算法流程Fig.1 PSO algorithm flow

1.3 级联型随机共振系统

级联型随机共振系统通过把多个单级随机共振系统串联，将前一级的输出信号作为后一级的输入，每当原始信号经过一级随机共振系统时，就会产生部分能量的跃迁。若串联的级数适当，处于高频段的噪声就会得以减弱，低频段的信号能量就能够得到加强，从而增强随机共振的效果。同时由于随机共振的特性，低频段的信号容易产生共振现象。

级联系统各级对应的朗之万方程为

(9)

式(9)中，第一级的输出x1(t)作为第二级的输入，以此类推，第n-1级的输出xn-1(t)又作为第n级的输入。

在对两级级联随机共振系统仿真测试中，设输入信号信噪比-20 dB，在经过第一级随机共振后输出信噪比为-18.61 dB，经过第二级随机共振后系统输出信噪比为-11.95 dB。输出信号信噪比有了较大的改善，由此证明了级联型随机共振系统的可行性。

2 级联型自适应随机共振系统

通过运用粒子群算法来自适应地调节变尺度随机共振系统，即粒子群随机共振系统(PSR)的提出，可以快速准确地解决未知频率水下目标信号的检测问题。PSR算法流程如图2所示，本文方法较传统随机共振方法优越的部分在于可以自动寻找a、b、k的最佳值，通过对每次寻找到的a、b、k值都进行系统输出信噪比的计算并以此作为目标优化函数，根据信噪比的大小判定当次a、b、k值是否需要保存，直至找到最佳参数。在理论上可以使系统处于最优的随机共振状态，准确率高且能根据不同频率的信号选择最佳的参数。

图2 粒子群随机共振算法流程Fig.2 PSR algorithm flow

当实际待检测信号的信噪比很低时，经过一次随机共振系统处理往往不能使得系统产生较好的随机共振现象，不能从中提取到有用的线谱成分。为了解决上述问题，本文将粒子群算法随机共振系统进行级联，通过相关仿真测试以及理论分析综合考虑后，采取对随机共振系统进行二级级联增强。通过分别对两级随机共振系统参数进行寻优，第一级寻优参数为a1、b1、k1，第二级为寻优参数为a2、b2、k2，进而使系统的输出信噪比达到最大。系统原理如图3所示。

图3 级联型粒子群随机共振系统Fig.3 Cascaded PSR system

3 仿真分析

设系统的输入信号为S(t)=x(t)+Γ(t)，其中x(t)是幅值A=0.5，频率f0=100 Hz的高频正弦信号，Γ(t)是零均值高斯白噪声，输入信号信噪比设置为-20 dB。系统输入信号时域波形如图4所示，其相对幅度频率谱如图5所示。

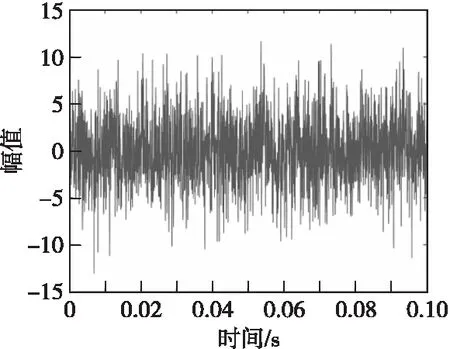
图4 系统输入信号时域波形Fig.4 Time domain waveform of input signal in stochastic resonance systems

图5 随机共振系统输入信号的相对幅度-频率谱图Fig.5 Relative amplitude-frequency spectrum of input signals in stochastic resonance systems

采用级联型粒子群随机共振方法检测上述的输入信号，系统参数配置如下：采样频率fs=20 kHz，种群规模250，进化次数100，学习因子c1=c2=0.5，最大权重ωmax=0.5，最小权重ωmin=0.1。结合仿真测试结果，设置a的寻优范围为[0,1]，b的寻优范围为[0,1]，k的寻优范围为[0,1]。

观察级联型自适应随机共振系统的输出效果如图6—图11所示。

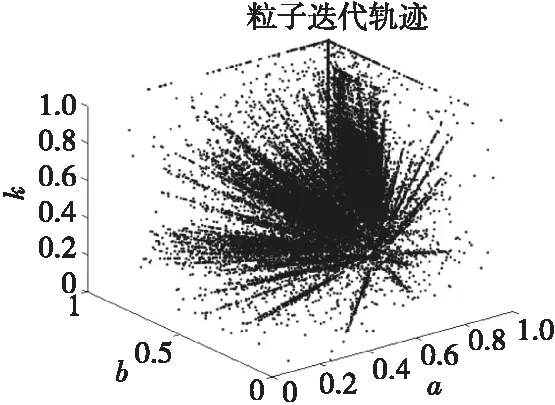
图6 第一级粒子群随机共振系统参数寻优Fig.6 Parameter optimization of the first order PSR

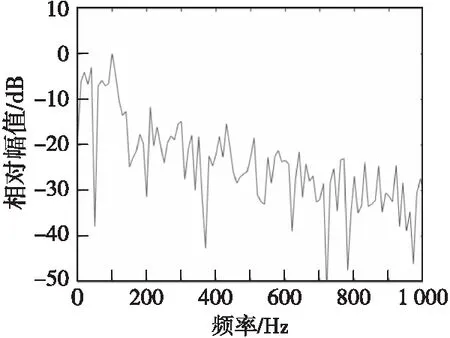
图8 第一级粒子群随机共振输出信号的相对幅度-频率谱图Fig.8 Relative amplitude-frequency spectrum of the output signal in the first order PSR

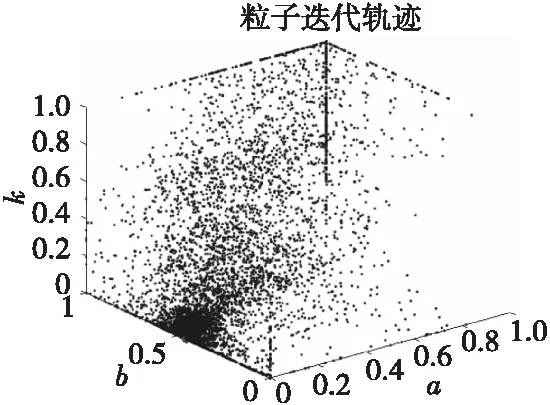
图9 第二级粒子群随机共振系统参数寻优Fig.9 Parameter optimization of the second order PSR

图10 第二级粒子群随机共振后的输出信号Fig.10 Output signal of the second order PSR

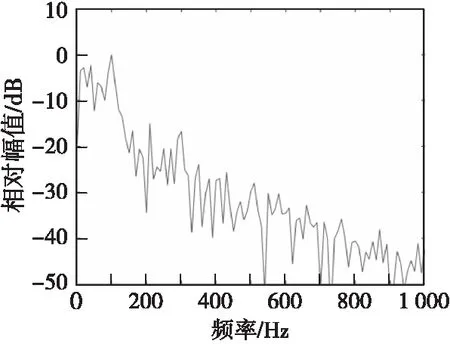
图11 第二级粒子群随机共振输出信号的相对幅度-频率谱图Fig.11 Relative amplitude-frequency spectrum of the output signal in the second order PSR

根据实验得到：第一级粒子群随机共振系统参数为a1=0.963 9，b1=0.694 2，k1=0.001 6时，待检测信号通过后信噪比由-20 dB提高到-12.44 dB；第二级粒子群随机共振系统参数为a2=0.000 1，b2=0.454 1，k2=0.000 4，最终输出信号的信噪比可提升到-10.41 dB。

由以上结果可以看出，原始输入信号经过级联型粒子群随机共振后，在输出信号频谱图中，高频区域的能量被搬移增强到待测信号频率范围内，在待检测100 Hz频率处有明显的信号能量谱峰，并且在输出信号时域波形中，待检测目标信号波形其内在的周期性得到进一步增强凸显。级联型粒子群随机共振方法能够大幅度的提高输出信噪比，使系统的最终输出信噪比达到-10.41 dB，相比于输入信噪比-20 dB有较大的提高。由此可得出结论，级联型粒子群随机共振方法对于未知频率低信噪比信号的检测有很好的效果，能够有效对含噪信号进行线谱增强。

4 结论

随着现代海战不断发展带来的挑战，目标隐身技术提高以及日趋增强的海洋环境噪声的影响，接收到的水下目标辐射噪声信号信噪比大大降低，直接影响水雷武器的性能。随机共振方法可使微弱周期信号在噪声的协助下在势阱之间跃迁，增强微弱信号的信噪比，实现微弱周期信号的检测。

本文提出的级联型粒子群随机共振方法，可以针对水下目标信号信噪比低且未知频率的情况，利用粒子群算法自适应地调整系统参数，解决了随机共振系统最优参数标定困难的问题，并且通过系统级联有效地提升了水下目标信号的信噪比。现代水雷探测技术在很大程度上依赖水声探测技术的发展，对被动声引信水雷而言，利用本文方法对低信噪比水下目标的探测工作具有可行性和可靠性，对被动声引信水雷的设计有一定的参考价值。