基于能量域的引信环境识别

宫雪峰，李豪杰，陈志鹏，于 航，原红伟

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

引信是利用环境信息、目标信息或平台信息，确保弹药勤务和弹道上的安全，按预定策略对弹药实施起爆控制的装置，是弹药控制起爆的“大脑”，是保证武器装备和弹药安全与完成毁伤的关键核心部件[1-3]。

引信的安全性至关重要。随着技术的发展，战场的环境愈发变幻莫测，且随着新型武器如巡飞弹、无人机、小型无人机战车的出现，引信使用过程中经历的环境逐步体现出幅值越来越小，持续时间更长的弱环境特征；与此同时，安全系统控制需求越来越强，表现为实现安全系统状态转换的准确性和快速性，需要对安全系统进行精细化设计。在这种背景下，对弱环境识别的研究被推上热潮，也开启了对引信设计理论和方法展开创新性研究的第一步[4-5]。

目前，国内已经对安全系统的识别理论和作用原理开展了大量研究。在引信安全控制与环境识别理论的研究方面，文献[6]中基于一款导弹弹头引信，设计了一种基于“阈值+顺序+时间窗”的电子安全系统，确保了导弹弹头引信的解保可靠性和勤务处理安全性。文献[7—8]中提出了“双阈值+时间窗”判别方法，改善了“单阈值+时间窗”识别方法可能发生环境误判的问题。文献[9]中提出一种基于“阈值与滑动时间窗”的发射过载特征识别方法，使得安全系统可以识别正与负的双向过载。这些研究内容为安全系统的识别方式做出了贡献，但这些识别方法仍旧是停留在阈值与时间窗的范畴内，都是基于常规高过载的发射环境下进行识别，在弱环境下识别可靠性未知，无法完全适应未来安全系统的精细化设计需求。

在作用原理的研究上，文献[10—12]分别对双自由度后坐保险机构、带曲折槽的惯性筒保险机构、空气阻力作为第二解除保险环境力等的可行性进行了分析，总结出了其保险机构的数学表达，为弱环境的结构设计方法提供了重要的理论基础。但是这些研究注重的是系统随时间的响应，未对解保过程背后的一些共性的原理深入探讨。

针对引信安全控制需求，本文提出一种基于能量域的环境识别方法，从能量的角度分析解除保险的工作原理，设计环境量积分方法与环境特征逻辑判别方法，为安全系统设计提供一种新的途径。

1 安全系统中的能量利用

引信与外界的交互形式主要表现为信息交互、能量交互和物质交互三种。信息交互就是安全系统通过传感器将外界环境信息获取后再现，或通过通信模块实现信息的发送与接收；能量交互就是引信直接受到外界环境效应产生的能量转换过程，如引信安全系统将发射过程的机械能转换为弹性势能、热能、电能等并储存或利用；物质交换指的就是如在起爆过程中火焰、物理碎片外飞等产生物质上的交互。在目前成熟的解保过程中，机械安全系统在大多数情况下能量的交互占主体地位，主要为对机械能的利用，而在机电式和电子式安全系统中同时具有信息交互能力。

引信安全系统对机械能的利用，如机械安全系统中的双自由度后坐保险机构、带曲折槽的惯性筒机构和离心力驱动的软带等机构，它们的作用原理是在外力的做功下，保险件的动能和势能与弹簧的弹性势能相互转换从而解除保险，此外，风翼旋翼是将风能转化为机械能解除保险，弹丸的发射过程就是一个化学能转化为弹丸机械能的过程；电能的利用，典型的如利用涡轮机构将风能转化为电能实现供电功能；热能的利用，主要也是在弹丸飞行过程中，由于空气阻力的影响，风能转化为内能，实际应用如利用易熔金属在空气摩擦的作用下会熔化的现象实现解除保险。

现有的安全系统对环境信号的识别，通常是判断环境力的值是否在一定的阈值之上并达到一定的时间，若从能量角度分析，可以分析在到达一定时间时，某个环境激励是否具有一定的能量。因此，可以设在某一时刻使安全系统为外界所给予的能量为E，其需要高于安全系统实现解保时的最小能量需求Emin：

E>Emin，

(1)

式(1)中，E能量形式是根据需求得来的，通常情况下E可以根据某一种物理量对时间t的积分量得来。表1例举出了一些引信安全系统常用的环境量及其积分后的物理意义和积分量可以表达的能量形式。

表1 部分环境量对时间积分代表的物理意义Tab.1 Physical significance of partial environmental quantity to time integral

对加速度a积分，可获得当前的弹丸速度，计算mv2/2即可计算此时的弹丸动能；对速度v积分获得此时的位移x，虽不能指代任何能量但可以得到弹丸的位移；速度的平方v2与弹体表面的温度成正比，根据温度曲线可以计算易熔合金的内能；速度的三次方v3与涡轮发电功率成正比，对时间积分则可以计算出发电量从而计算总电能。

根据以上分析，此处的能量为广义能量的概念，物理意义上不一定是物理量中能量的表示。

2 基于能量域的识别方法

2.1 总体设计

根据上一章的分析，提出基于能量域的引信环境识别系统，通过多次获取环境参数并处理进行综合判断，系统原理如图1所示。

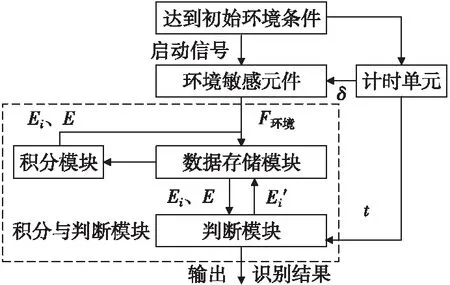
图1 基于能量域的引信环境识别系统原理Fig.1 Principle of fuze environment recognition system based on energy domain

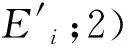
2.2 积分与判断模块

对于安全系统而言，对一种信号进行采集最终得到的数据是离散的点，采样频率越高点越密集。引信安全系统需要准确性与实时性并存，因此，需要选择一种步骤简单、处理速度快、误差小的积分方法，本文选用了梯形法进行近似积分计算。

如图2所示，在区间[T1，T2]内的定积分的几何意义就是曲线在区间[T1，T2]间与横坐标围成的面积，每个离散环境量之间都间隔一个固定的时间δ，正好把环境信息曲线分割成了许多等距的小区间。

图2 梯形法近似积分Fig.2 Trapezoidal approximate integral

离散的后坐过载值组a={a1,a2,…,an},则每一个离散区间的面积Ei和当i=n时的总积分值E(n)为

(2)

为了进行实时判断，根据级数定义有

(3)

因此，采用实时的梯形法积分识别环境也是一个迭代的过程，Ei就是实时的单元环境积分量，根据式(3)，判断模块流程如图3所示。

图3 积分与判断模块Fig.3 Integral and Judgment Module

首先需要确定起始阈值F0，对于机电安全系统需要在膛内上电后使用，可以取F0=0。i代表了第i次记录环境量与第i次迭代计算积分值。tmax代表容许识别时间上限，δ为采样周期，其值都根据引信具体使用环境来确定，Tempi表达的是当前循环的梯形单元积分量，也就是式(2)中的Ei，Emin指的是设定的最小积分阈值，ΔEmax指的是容许的积分值变化最大值，S为设定的安全裕量系数，env是环境识别的输出，当env为1时代表识别到了正确的发射环境，为0时代表未识别到或者发生故障。

第一个判断单元Tempi>ΔEmax的功能是判断当前输入的积分量是否大于容许的积分值变化最大值。如果超过了，则用上一次积分值代替这一次积分值，可以滤去一些短时大峰值的，即瞬时积分量过大的瞬时脉冲信号；如果没超过，则用式(2)算出当前的总环境积分量。

第二个判断模块E(i)/S>Emin的意义在于判断当前的积分量是否已经超过了设定的最小积分阈值。如果超过了则说明判断出了正确环境；如果没超过则需要进入第三个判断模块。

第三个判断模块i·δ>tmax用来检验当前环境识别时间i·δ是否超过了设定的最大环境识别时间窗tmax。如果超过了，则判断环境为错误发射环境，输出env=0；如果没超过，则i=i+1进行重复迭代。

3 仿真验证

为验证本文提出的方法，本章以低过载火箭弹发射过载为例，将正常弱发射环境的过载作为输入来验证本文识别方法可靠性和快速性，将欠加速与过加速环境作为输入来验证本文识别方法具有自适应减小解保位置散布的能力，对停机故障情况进行仿真来验证本文识别方法的故障环境识别能力，跌落过载作为输入来验证本文识别方法的安全性。

3.1 正常弱发射过载仿真

表2给出了相关文献中仿真验证环节所取的发射环境模拟量和勤务处理跌落环境模拟量，以及验证所得的解除保险时间。

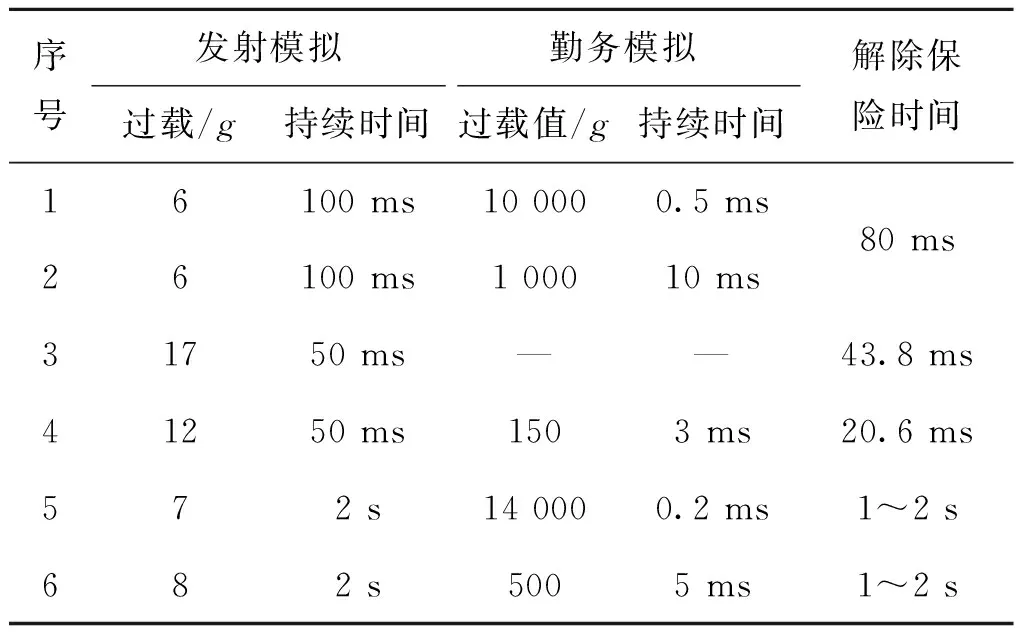
表2 部分过载模拟量大小及持续时间和解保时间[13-16]Tab.2 Partial overload analog size and duration and arming time

从表2中可以看出，大部分仿真实验都将弱环境发射的过载量看作一个持续过载信号。结合表2数据，使用数值仿真软件，选取发射过载为10g，持续时间50 ms，采样频率选择1 ms处理，结合实际发动机助推过载曲线，在理想的发射过载曲线上增加一些正弦叠加噪声，得到如图4的拟合发射过载曲线。

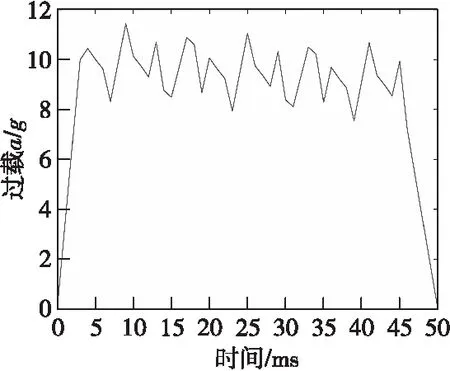
图4 拟合发射过载曲线Fig.4 Fitted launch overload curve

在表2中，后两种模拟环境时间太长，使用前4种发射过载模拟量乘以对应的持续时间可得：前两种的积分量值(速度大小)为600g·ms，第3种为850g·ms，第4种为600g·ms，且解除保险时的积分量值(速度大小)前两种为480g·ms，第3种为744.6g·ms，第4种为247.56g·ms。本文选取的环境与第4种模拟环境类似，因此选最小解保积分量阈值和安全系数的乘积S·Emin为250g·ms，容许最大瞬时积分增量同样根据第4种的勤务环境模拟量150g，再根据保守原则ΔEmax取100g·ms，最大环境识别时间tmax为50 ms，处理结果如图5所示。

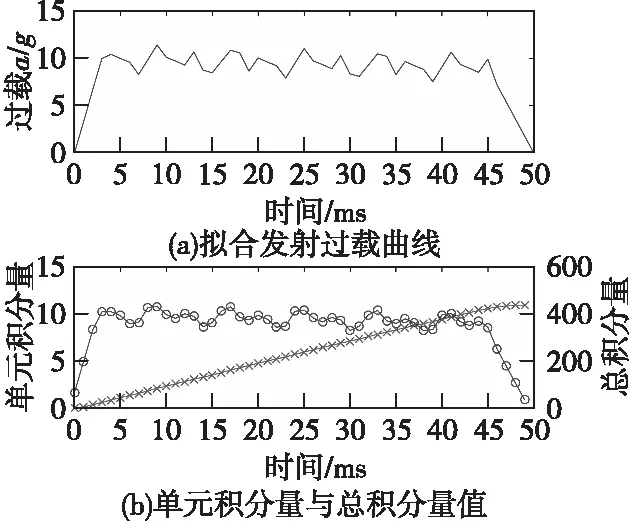
图5 发射过载识别结果Fig.5 Launch overload recognition results

图5(b)左侧纵坐标为单元积分量Ei(即流程图中的Tempi)随时间的变化，在坐标中通过圆和连线表示。右侧纵坐标为到达ti时总的积分量E(i)，在坐标中通过叉和连线表示。该处理方法在26 ms时判定该环境为有效环境，处理数据到输出结果用时15 ms，在41 ms时输出环境识别结果，处理迅速，能够满足在50 ms内的解保任务。

3.2 欠加速和过加速过程仿真

由于种种因素影响，发射环境的过载不一定稳定，会存在欠加速和过加速的情况。欠加速时，环境单元积分量Ei变小，环境积分量E(i)增长到最小环境积分阈值Emin的时间t变大，反之，过加速度时，识别时间t变小。根据位移增量与时间的关系Δx正比于加速度a且正比于时间的平方t2可得，若想位移增量稳定，加速度a变大时t要减小，a减小时t要变大，本文的识别方法刚好可以满足让位移增量稳定的基本条件。

为了验证本文识别方法相较于“阈值+时间窗”识别方法的优势，在此选取±15%的欠加速和过加速情况进行分析[17]，仿真结果如图6所示。

图6 欠加速与过加速识别结果Fig.6 Under-acceleration and over-acceleration recognition results

在欠加速情况下，积分量增长得比较慢，增长到判定阈值的时间是29 ms，过加速积分量到阈值的时间是23 ms，都与正常情况下的识别时间相差3 ms左右，计算时间15 ms，仍能保证50 ms内解保。

根据积分的定义，输入是加速度，积分后获得的是速度曲线，再次积分便可获得位移，对图6的欠加速和过加速以及正常发射过载的速度量再次积分，即可获得解除保险时弹丸已移动的位移，积分方法识别与“阈值+时间窗”识别方法在三种情况下的解除保险距离对比如表3所示，“阈值+时间窗”识别方法解保时间取正常环境下积分识别解保时间41 ms。

表3 两种识别方法解保距离对比Tab.3 Comparison of two recognition methods to solve the arming distance

由表3可以看出，相较于正常过载下的解保距离，本文的识别方法能够有效地改善解保距离散步大的问题，相较于“阈值+时间窗”识别方法最大相对误差15.5%，本文识别方法能将解保距离散步降低至6.8%以内。

3.3 停机故障仿真

为验证本文识别方法可以识别异常发射故障，对停机故障情况进行仿真。停机故障可以参考火箭弹助推器停机故障，重点关注初始段停机和中段停机。发生初始段停机时，取环境量在0～3 ms时处于升高过程，后因停机在10 ms时环境量归为0。中段停机取在23 ms前处于正常工作状态，在23 ms时停机，在30 ms时过载值归为0。根据上述环境，环境量的积分情况如图7所示。

图7 初始段与中段停机识别结果Fig.7 Recognition results of initial and intermediate stoppages

在这两种情况下，最终环境被系统判定为非正常环境，原因为两种情况的环境量积分结果E(i)都不能在最大容许识别时间上限tmax(50 ms)前达到最小解保积分量阈值Emin与安全系数S的乘积，所以只要参数设置合理，本文识别方法能够行使对故障环境的识别功能。

3.4 跌落环境仿真

为证明识别的安全性，加载模拟跌落信号输入。根据表2的跌落环境，同样选择最为极端的两种模拟情况，分别为10 000g过载、持续0.5 ms和300g过载、持续5 ms。

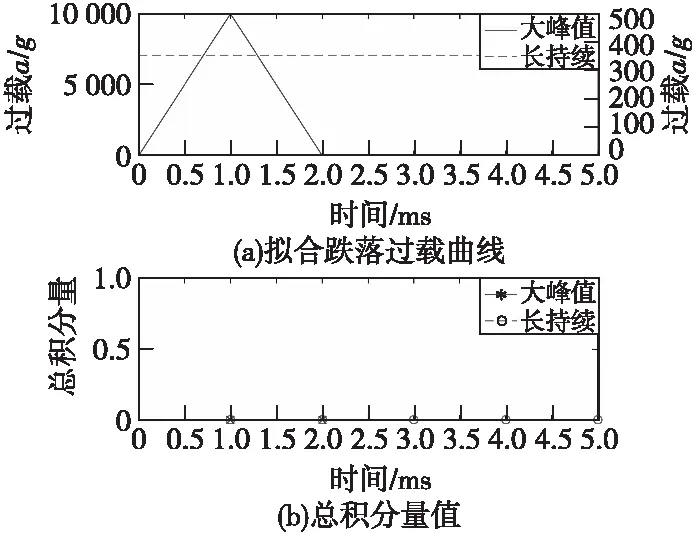
图8 两种过载情况下的识别结果Fig.8 Recognition results in two overload situations

图8(a)是模拟采集到的跌落信号，图8(b)是积分量值，可以看出，因为两种环境瞬时的单元积分值Ei全程大于容许的积分变化最大值ΔEmax，系统将异常的增量过滤掉，全程的积分量E(i)计算结果都是0，之后输出低电平信号，证明该识别方法可以保障勤务处理中跌落时的安全性。

本文中加载的模拟跌落过载曲线虽然并非是以能量法衡量时能量最大的过载曲线，但即使跌落过载具有比弱发射过载过程中更多的能量，由于该识别方法并非只是对能量的值进行判断，还存在对能量瞬时变化的判断，因此基于上述两个判断依据，即使勤务处理过程中存在环境能量增加更快、总能量更大的情况，其能量特征仍与弱发射过程中的过载存在较大的区分度，系统不会做出解保响应。

4 结论

本文提出一种基于能量域的环境识别方法。该方法利用梯形法对环境量进行近似积分计算，要求每一次积分量值Ei不大于最大允许的积分变化值ΔEmax，识别时间不超过最大允许识别时间tmax，判断是否满足E/S>Emin。实验结果表明，本文的识别方法能够在给定模拟的弱发射过载环境下快速、准确地给出解保信号，降低了在过、欠加速发射环境下的解保距离散布大的问题，由“阈值+时间窗”方法的15.5%降低到了6.8%，可以识别异常情况下的初始段和50%段停机发射过载，能够保障勤务处理时的跌落安全性。证明了基于能量域的环境识别方法的可行性，为引信安全系统提供了一种新的设计思路，并为解保策略的设计提供参考。