基于改进ADC 模型光电对抗系统作战效能评估方法 *

宋振之，韩道文 ，鲍俊臣 ，黄朝阳

（1. 国防科技大学，安徽 合肥 230000；2. 中国人民解放军31649 部队，广东 汕尾 516600；3. 陆军勤务学院，重庆 400041）

0 引言

随着现代战争向智能化不断发展，光电武器日新月异，成为制胜战场的重要手段。在此背景下，光电对抗系统的研究也受到越来越多国家的高度重视。如何准确评估光电对抗系统的作战效能是当前急需解决的重要问题。当前，对武器系统作战效能评估的主要方法有层次分析法［1］、模糊综合评判法［2］、灰色评估法［3］、德尔菲法［4］、指数法［5］、模拟仿真法［6］和ADC 法［7］等。在光电对抗领域，文献［8］建立了光电对抗装备效能评估的体系框架，但是没有给出具体的评估方法；文献［9］和文献［10］分别基于GAHP（grey analytic hierarchy process）和模糊综合评价法对光电对抗系统作战效能进行了评估；文献［11］利用“联合指数”法对联合作战中光电对抗系统作战效能进行了量化分析；以上文献大多围绕装备固有效能展开分析，没有考虑作战运用和人的因素对装备作战效能的影响。文献［12］利用ADC 法和模糊综合评判法对光电对抗系统作战效能进行了分析，但是可用度与可信度矩阵计算均过于简化，致使评估结果与装备实际误差较大。

本文从实战的角度出发，在传统ADC 法的基础上考虑了实际中光电对抗系统多个设备串并联，通过整合状态的方式减少中间态的数量，并充分考虑了战术运用和人员操作对装备作战效能的影响，提出了一种改进的作战效能评估方法，可为光电对抗系统作战效能评估提供参考。

1 ADC 模型及其改进方法

1.1 传统ADC 模型

ADC 模型是美国工业界武器系统效能咨询委员会建立的对武器系统作战效能评估的模型，这个模型被公认为是最有效的模型，至今仍在武器系统效能分析中广泛运用［13］。该模型认为武器系统的作战效能（E）是其可用性（A）、可信性（D）以及作战能力（C）的乘积，其表达式为

可用性A 通常用向量表示，是对武器系统在开始执行任务时所处工作状态或可承担任务状态的量度，主要反映武器系统使用准备的程度。其表达式为

式中：ai为武器系统开始执行任务时处于第i 种状态的概率，易知

可信性D 通常用矩阵表示，是对武器系统在执行任务初处于某一状态而任务要求有输出时处于另一种状态的转移性指标，主要反映武器系统的可靠性的优劣。其表达式为

式中：dij为在执行作战任务时，武器系统由第i 种状态转变成第j 种状态的概率，易知矩阵每一行的和为1，即

作战能力C 通常用列向量表示，是对武器系统固有能力的描述，表示在不同状态条件下完成指定任务能力的量度，反映了武器系统设计能力与作战实际要求之间的符合程度，其表达式为

式中：ci为武器系统处于第i 种状态时完成任务的能力。

1.2 改进ADC 模型

光电对抗系统在作战时的效能发挥不仅跟其可用性、可信性、能力有关，还受系统作战运用的影响，例如系统的配置是否恰当，决定了系统防护的范围能否全面覆盖被保护目标，以及干扰信号能否进入来袭目标的视场。干扰时机把握得好不好，决定了干扰信号能否进入来袭导弹的时间波门。参数选择合不合适，决定了干扰信号与干扰对象的光电系统是否匹配，干扰是否有效。光电假目标和诱饵使用决定了系统自身防护等。此外，武器系统的作战效能还受到人员操作的影响，例如操作人员专业水平、心理身体素质、系统自动化程度、系统人机交互流畅度等都对系统作战效能的发挥产生影响。传统ADC 模型在对光电对抗系统作战效能进行评估上时，没有充分考虑这些因素对装备作战效能的影响，会导致评估结果与作战实际产生偏差，因此，本文将这2 项因素纳入对光电对抗系统作战效能评估，更符合光电对抗系统的作战实际。本文建立的光电对抗系统作战效能评估指标体系如图1 所示。

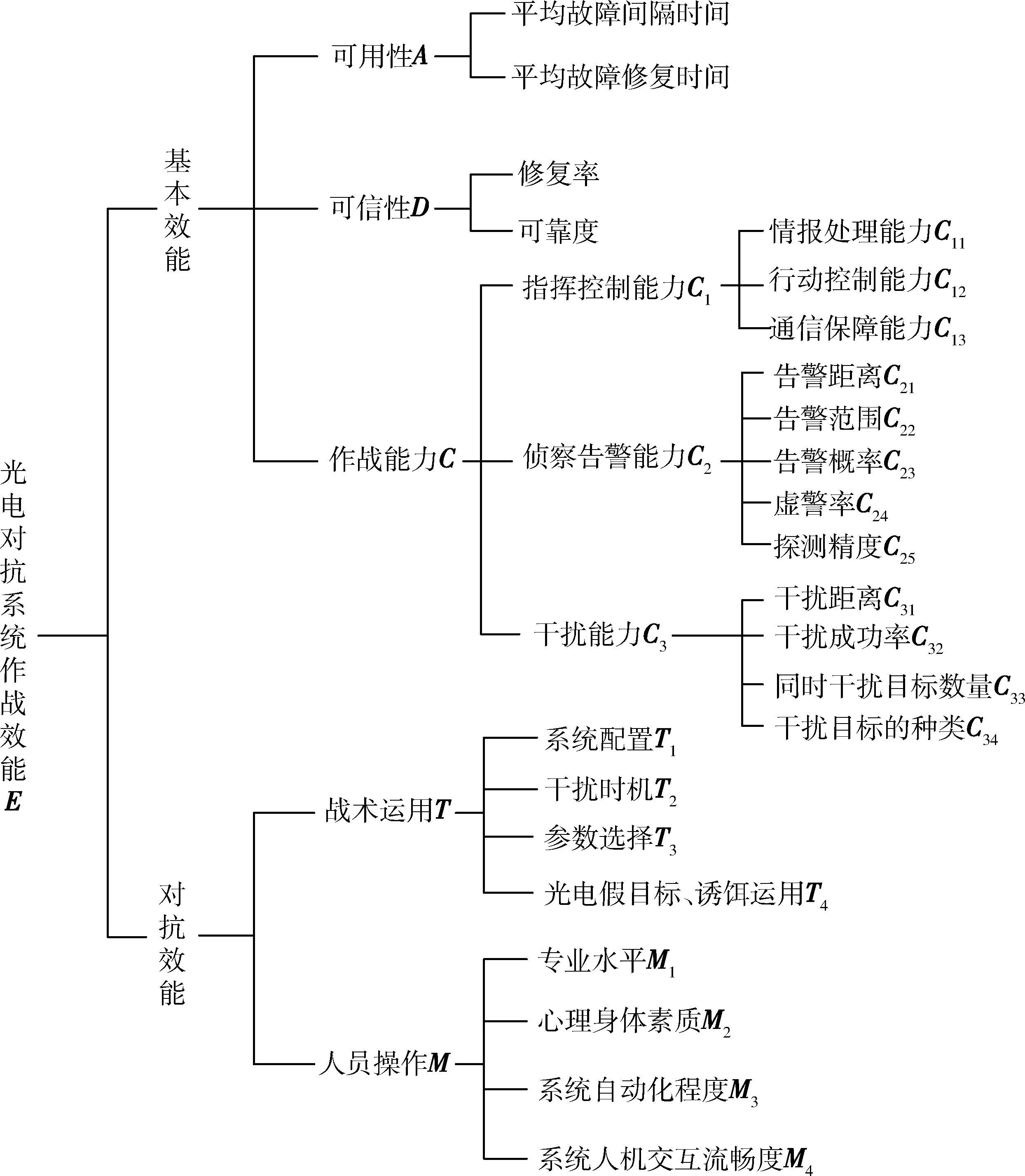
图1 光电对抗系统作战效能评估指标体系Fig. 1 Indicator system for evaluating the combat effectiveness of the electro-optic countermeasure system

一些文献将环境的影响单独作为武器系统作战效能的影响因素［14-15］，但是对于光电对抗系统而言，环境的影响已经包含在作战能力C里了，这里不再单独体现。例如大气能见度会对光电对抗系统的告警距离、干扰距离产生影响等。因此，改进后的光电对抗系统作战效能表达式为

式中：T为战术运用影响因素；M为人员操作影响因素。

2 光电对抗系统效能评估

2.1 光电对抗系统组成及其状态分析

2.1.1 光电对抗系统组成

光电对抗系统通常由指挥控制分系统、侦察告警分系统、干扰分系统串联组成，其中指挥控制分系统通常由1 台指挥控制设备组成，侦察告警分系统通常由多个侦察告警设备并联组成，干扰分系统通常由多个干扰设备并联组成。为了便于分析计算，假定侦察告警分系统包含2 个侦察告警设备、干扰分系统包含3 个干扰设备，且相同类型设备型号性能一样，则典型光电对抗系统的组成如图2所示。

图2 典型光电对抗系统组成Fig. 2 Composition of a typical electro-optic countermeasure system

2.1.2 光电对抗系统状态分析

假设各设备之间工作状态互不影响，每台设备都有正常的2 种故障工作状态，则光电对抗系统共有26= 64 种工作状态，分析起来极为不便。但是通过分析可以发现，由于系统中各设备既包含串联又包含并联关系，因此，其中处于串联设备或一个分系统内所有并联设备发生故障，则整个武器系统就会发生故障。另外，因相同类型设备型号性能一样，其中相同类型的任何一个设备故障，对武器系统的总体作战效能影响程度一样。因此，可以对武器系统一些工作状态进行整合，从而减少工作状态的数量。由图2 可分析得到光电对抗系统工作状态如表1 所示。

表1 光电对抗系统工作状态表Table 1 Electro-optic countermeasure system working status table

2.2 光电对抗系统效能评估指标分析

2.2.1 系统可用性A分析

根据前文分析，光电对抗系统共有7 种状态，即A=［a1，a2，…，a7］，分别对应状态1 至状态7 出现的概率，而每个设备均有正常和故障2 种状态。设p1，p2，p3分别为指挥控制设备、侦察告警设备、干扰设备处于正常 工作的概率；MTBF1，MTBF2，MTBF3分别为指挥控制设备、侦察告警设备、干扰设备平均无故障工作时间；MTTR1，MTTR2，MTTR3分别为指挥控制设备、侦察告警设备、干扰设备平均修理时间；λ1，λ2，λ3分别为指挥控制设备、侦察告警设备、干扰设备故障率；μ1，μ2，μ3分别为指挥控制设备、侦察告警设备、干扰设备修理率。则有

因此，可得

2.2.2 系统可信性D分析

假设光电对抗系统在执行作战任务过程中无法进行修复，系统故障服从指数定律，即

式中：Ri为设备的可靠度；i分别为指挥控制设备、侦察告警设备、干扰设备；t为系统执行任务的时间。

则光电对抗系统由状态1 转变为其他状态的概率为

光电对抗系统由状态2 转变为其他状态的概率为

光电对抗系统由状态3 转变为其他状态的概率为

光电对抗系统由状态4 转变为其他状态的概率为

光电对抗系统由状态5 转变为其他状态的概率为

光电对抗系统由状态6 转变为其他状态的概率为

光电对抗系统由状态7 转变为其他状态的概率为

2.2.3 系统作战能力C分析

根据前文分析，光电对抗系统的作战能力可划分为指挥控制能力、侦察告警能力、干扰能力。指挥控制能力又进一步划分为情报处理能力、行动控制能力、通信保障能力；侦察告警能力划分为告警距离、告警范围、告警概率、虚警率、探测精度；干扰能力划分为干扰距离、干扰成功率、可同时干扰目标数量、干扰目标的种类。其中，指挥控制能力中的3 个指标属于定性类指标，而侦察告警能力中的5个指标和干扰能力中的4 个指标为定量类指标，定量类指标中又有数值越大越好的效益型指标（如告警距离、告警范围等）还有数值越小越好的成本型指标（如虚警率、探测精度）。对不同的指标类型计算的方式不同，下面区分定性类、定量类指标分别分析。

（1） 定性类指标

采取模糊综合评判法结合层次分析法进行评定，具体方法如下。

step 1： 根据图1，建立光电对抗系统指挥控制能力评估因素论域U1=｛u11，u12，u13｝。

step 2： 建立指标的评语等级论域V

V=｛v1，v2，v3，v4｝=｛0.9，0.8，0.6，0.4｝=｛优，良，一般，差｝。

step 3： 邀请多名专家对设备正常工作时指挥控制能力进行打分，建立单因素评判模糊关系矩阵R为

式中：ri，j为指挥控制能力中的3 个指标对应评语等级论域中的隶属度。

step 4：运用层次分析法，通过专家打分评判，确定指挥控制能力评估因素论域U1中3 个指标的权重W1=（w11，w12，w13），其中w1j＞0 且

step 5： 通过选择合适的“模糊合成算子”计算指挥控制能力的最终得分。本文选取合成算子“°”，即若，则做归一化处理。

step 6： 计算指挥控制能力值

（2） 定量类指标

对不同类型指标进行归一化处理，再结合层次分析法进行评定，具体方法为：

step 1： 确定指标类型

将评判的指标分别区分为效益型指标和成本型指标。

step 2： 对指标归一化处理

对效益型指标，其归一化公式为

式中：xij为第i类能力第j个指标在设备正常时相应指标值，该值可通过演习或装备试验得到；mij，Mij分别为指标可取的最小值、最大值。

对成本型指标，其归一化公式为

step 3： 确定侦察告警能力各子能力指标的权重W2=（w21，w22，w23，w24，w25）和干扰能力各子能力指标权重W3=（w31，w32，w33，w34）。

step 4： 分别计算侦察告警、干扰能力值

（3） 作战能力计算

step 1： 根据装备所处的状态建立能力矩阵

系统在不同状态下，各项能力有不同数值。设指挥控制设备正常工作，时系统的指挥控制能力为C1；当只有1 台侦察告警设备正常工作时，系统侦察告警能力为C2（1）；2 台侦察告警设备均正常工作时，系统侦察告警能力为C2（2）；当只有1 台干扰设备正常工作时，系统干扰能力为C3（1）；有2 台干扰设备正常工作时，系统干扰能力为C3（2）；3 台干扰设备均正常工作时系统干扰能力为C3（3），则系统处于不同状态时的能力数值如表2 所示。

表2 系统不同状态时的，能力值Table 2 Capability values for different state states of the system

其中，状态7 为串联分系统出现故障，因此整个系统处于故障状态，各分系统无法发挥作战效能，因此可以将其简化为所有能力值为0。

step 2： 运用层次分析法，确定指挥控制能力、侦察告警能力、干扰能力指标的权重分别为w1，w2，w3。

step 3：计算系统作战能力向量C：

式中：c1（si），c2（si），c3（si）分别为武器系统处于si状态时，指挥控制能力、侦察告警能力、干扰能力的数值。

2.2.4 系统战术运用T和人员操作M分析

系统战术运用主要计算在实际作战中运用的战术对系统作战效能产生的影响。可结合战场实际情况或通过专家评判得到系统配置、干扰时机、参数选择3 个指标具体分值和权重，再根据加权平均法求得战术运用系数T：

式中：αi为各项指标的权重；Ti为各项指标具体分值，取值范围为0~1。

人员操作主要体现人的因素对武器系统作战效能的影响。其求解方法与战术运用因素类似：

式中：βi为各项指标的权重；Mi为各项指标具体分值，可根据操作人员往年的训练考核成绩和军事演习表现情况确定，取值范围为0~1。

3 实例验证评估

3.1 计算系统可用度向量

假设某型光电对抗系统执行某项作战任务的时间为20 h，该型光电对抗系统各设备的技术指标如表3 所示。

表3 某型光电对抗系统技术指标Table 3 Technical indicators of a certain type of electrooptic countermeasure system

根据表3 中数据，由式（7）可得系统可用性A向量为

3.2 计算系统可信度矩阵

假设在执行任务过程中，设备不可修复。根据表3 中的数据，由式（8）~（15）可求得系统的可信性矩阵D为

3.3 计算武器系统能力矩阵

3.3.1 指挥控制能力

邀请100 名专家对武器系统指挥控制能力中的3 项评估指标进行打分评判，得到数据如表4 所示。

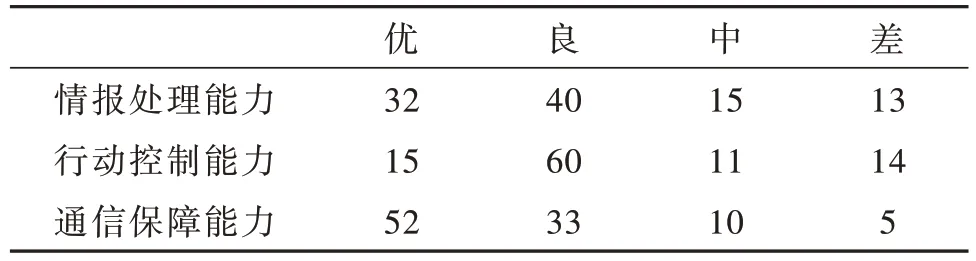
表4 武器系统指挥控制能力评判数据Table 4 Evaluation data on command and control capabilities of weapon systems

由此，可得到指挥控制能力单因素评判模糊关系矩阵R为

通过专家评判对3 个指标两两进行比较得到判断矩阵，如表5 所示。

根据表5 数据，可解得各指标的权重W1=（0.23，0.648，0.122），λmax=3.004，CR=0.003 8＜0.1，判断矩阵满足一致性要求。

表5 武器系统指挥控制能力判断矩阵Table 5 Weapon system command and control capability judgment matrix

进 而 求 得B=（0.234 24，0.521 06，0.117 98，0.126 72），再通过式（17）解得C1=0.846 5。

3.3.2 侦察告警能力和干扰能力

根据作战实际情况得到当前作战环境下该型光电对抗系统参数如表6 所示。

表6 某型光电对抗系统工作参数Table 6 Working parameters of a certain type of electro-optic countermeasure system

在侦察告警能力中，告警距离、告警范围、告警概率以及干扰能力中所有指标都是指标值越大越好，因此为效益型指标，可用式（18）进行归一化处理。侦察告警能力中虚警率、探测精度，指标值越小越好，为成本型指标，可用式（19）进行归一化处理。最终分别得到不同状态下，指标值归一化的结果为

同样通过层次分析法可以得到各项指标的权重，其方法与指挥控制能力权重计算方法一致，限于文章篇幅，这里省略具体步骤，直接给出计算后的权重值。

因此，再通过式（20），（21）可得到C2（1）=0.432 7，C2（2）=0.694 0，C3（1）=0.572 7，C3（2）=0.670 2，C3（3）=0.737 2。

3.3.3 计算武器系统能力向量

首先运用层次分析法，通过专家打分得到第1层指标的权重值W=（0.166 7，0.333 3，0.5），通过表2 和式（22）得到武器系统在不同状态下的能力矩阵C=（0.741，0.653 9，0.707 5，0.658 8，0.630 4，0.571 7，0）T。

3.4 计算系统战术运用与人员操作水平

通过演习检验得到系统战术运用与人员操作水平的数值，并进行归一化处理，再运用层次分析法，通过专家打分得到各指标权重如表7 所示。

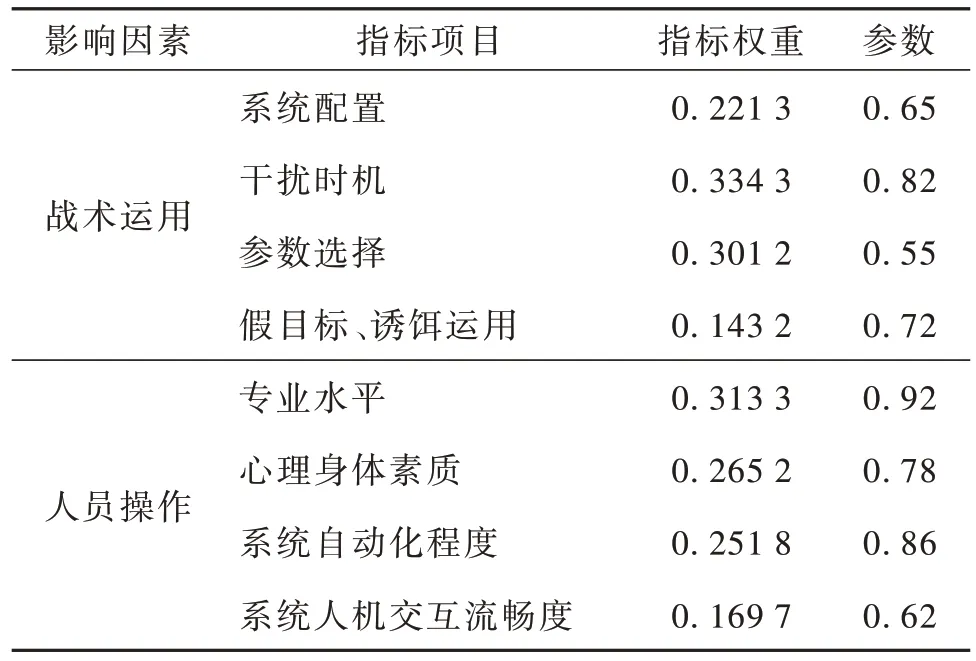
表7 光电对抗系统战术运用及人员操作因素指标权重表Table 7 Weight table of indicators for tactical application and personnel operation factors of electro-optic countermeasure system

根据表7 中的数据，并利用式（24），（25）分别计算得到战术运用T=0.686 7；M=0.816 9。

最后将得到的A，D，C，T，M代入式（5）得到该型光电对抗系统作战效能E=0.370 3。若不考虑战术运用和人员操作的影响得到的系统效能为E=0.686 7。

从评估结果可以看出，在考虑了战术运用和人员操作对武器系统的影响后，光电对抗系统作战效能相较传统的ADC 评估法得到的作战效能低。这是因为传统的ADC 评估法是在理想条件下，试验人员选择了最佳系统配置、干扰时机等战术，操作人员也发挥了最佳的操作水平的情况下，评估得到的系统作战效能，因而可以说是系统的固有效能。而在实战环境中受到战术运用的影响和人员操作的制约，光电对抗往往使系统无法发挥出最佳的效能，导致实际效能相比固有效能要低，这与本文评估得到的结果一致，验证了模型的有效性。因此，改进后的ADC 模型更贴近实战。

4 结束语

本文根据光电对抗系统作战效能评估的特点，将战术运用和人员操作作为单独的影响因素加以考虑，对传统的ADC 模型进行了改进。并在分析武器系统状态时充分考虑了多个设备串并联的实际情况，通过合并状态的方式简化计算量，最后通过实例验证了该方法的有效性。本文所提出的光电对抗系统评估方法较传统的ADC 法而言，考虑因素更为全面，具有较好的实用价值，可为光电对抗系统作战效能评估提供科学依据。