基于可拓云的合成旅装备保障能力评估方法研究 *
2023-03-06张耀龙阮拥军赵陆昊黄义松郭宇荣
张耀龙,阮拥军,赵陆昊,黄义松,郭宇荣
(陆军工程大学 石家庄校区,河北 石家庄 050003)
0 引言
装备保障能力作为体系作战能力的重要组成部分,其在联合作战中发挥的作用日益关键。新体制下,合成旅的装备保障呈现出保障力量构成多元、指挥控制复杂,装备种类繁多、保障任务繁重,技术日益复杂、保障难度增大以及分工明确精细、作业务求精准等特征,这对装备保障能力的生成发展提出严峻挑战。对当前合成旅的装备保障能力进行评估,分析制约装备保障能力发展的瓶颈,能够有效推动合成旅装备保障能力的加速生成[1]。
当前,对合成旅装备保障能力评估的研究成果丰硕,其中评估指标体系及指标权重的研究已经十分成熟,本文着重在评估模型方法方面进行相关的探究。在装备保障能力评估模型研究方面,国内学者成果比较丰富。左学胜等[2]基于对装备保障任务的建模分析,构建了装备保障能力评估模型,并采用模糊综合评判法对模型进行运算;赵师等[3]从体系作战对装备保障的要求出发,基于德尔菲法,通过计算累计贡献率,构建出评估指标体系,建立了BP(back propagation)神经网络模型,通过Matlab 进行了训练和仿真;宋星等[4]结合ADC(availability,dependability,capability)法 与模糊综合评判法构建了合成旅装备保障效能评估模型,通过对保障系统可用度、可信度及装备保障能力的乘积计算,确定装备保障能力评估结果;朱敦祥等[5]结合云理论与物元分析法,在利用熵值法与均方差法综合计算指标权重基础上,构建了基于云物元的评估模型,实现了对军民融合装备维修保障能力的评估。以上评估模型中,模糊综合评判法无法避免评估指标的模糊性,BP 神经网络训练与仿真过程中数据随机性考虑不足,ADC法中可用度与可信度在适用上存在局限性,云物元方法较好解决了以上相关问题,但是其最后单纯通过云关联度加权求和确定评估等级的算法,忽略了求解云关联度过程中存在的随机性,计算结果的可靠性无法验证。
针对以上问题,本文首先基于“任务-能力”的映射关系,构建了合成旅装备保障能力评估指标体系;综合运用层次分析法与熵权法计算评估指标的权重;然后,针对评估过程中评估指标等级标准区间的模糊性与随机性特点,结合物元可拓模型与云理论,构建了基于可拓云的合成旅装备保障能力评估模型,通过计算综合评判期望矩阵的期望值来确定最终评估等级,随后通过计算置信度来审核评估结果的可靠性;最后,通过对4 个同类型单位的实践评估,验证了模型的有效性。
1 评估指标体系构建
合成旅装备保障能力评估指标体系的构建,不仅要遵循科学性、客观性、完备性、独立性等基本原则,还应面向作战、面向实际装备保障任务,注重指标的可视化,遵循战建一致、可重复性、可观察性、可测量性等原则[6]。
结合作战任务实际,合成旅装备保障任务一般包含5 个模块:数据支撑模块(态势感知模块)、指挥控制模块、维修保障模块、供应(调配)保障模块、战场装备管理保障模块。数据支撑模块(态势感知模块),即通过战场信息网络体系搜集情报信息并进行处理,将处理后的信息传输至相关节点模块;指挥控制模块,在充分理解上级意图、分析判断形势,并对情报信息进行综合分析判断基础上,组织进行保障筹划、机动部署及行动控制,并通过网络信息体系将相关信息传递给其他模块;维修保障模块,受领各自任务后实施展开,分别输出修复装备、需后送(报废)装备、补给完的作战实体及状态良好的装备,并将动态数据通过保障网链传输给相应模块;指挥控制模块根据态势感知信息实现对具体保障行动的实时调控(见图1)。装备保障能力评估就是对各模块的保障行动及结果进行评估。

图1 合成旅装备保障任务模型Fig. 1 Composite brigade equipment support mission model
由于在实际任务展开中装备战场管理与其他任务存在交叉融合,一般由指挥要素组织实施,考虑将其纳入指挥控制能力的二级指标。因此,合成旅装备保障能力的主要内容应该包括指挥控制能力、维修保障能力、供应(调配)保障能力以及数据支撑(态势感知)能力等。具体能力指标内容可见文献[7]。
综上,通过构建合成旅装备保障任务模型,并对其进行细致分析,在相关原则指导下,可以构建出基于任务的合成旅装备保障能力评估指标体系[8],具体的指标设置如图2 所示。
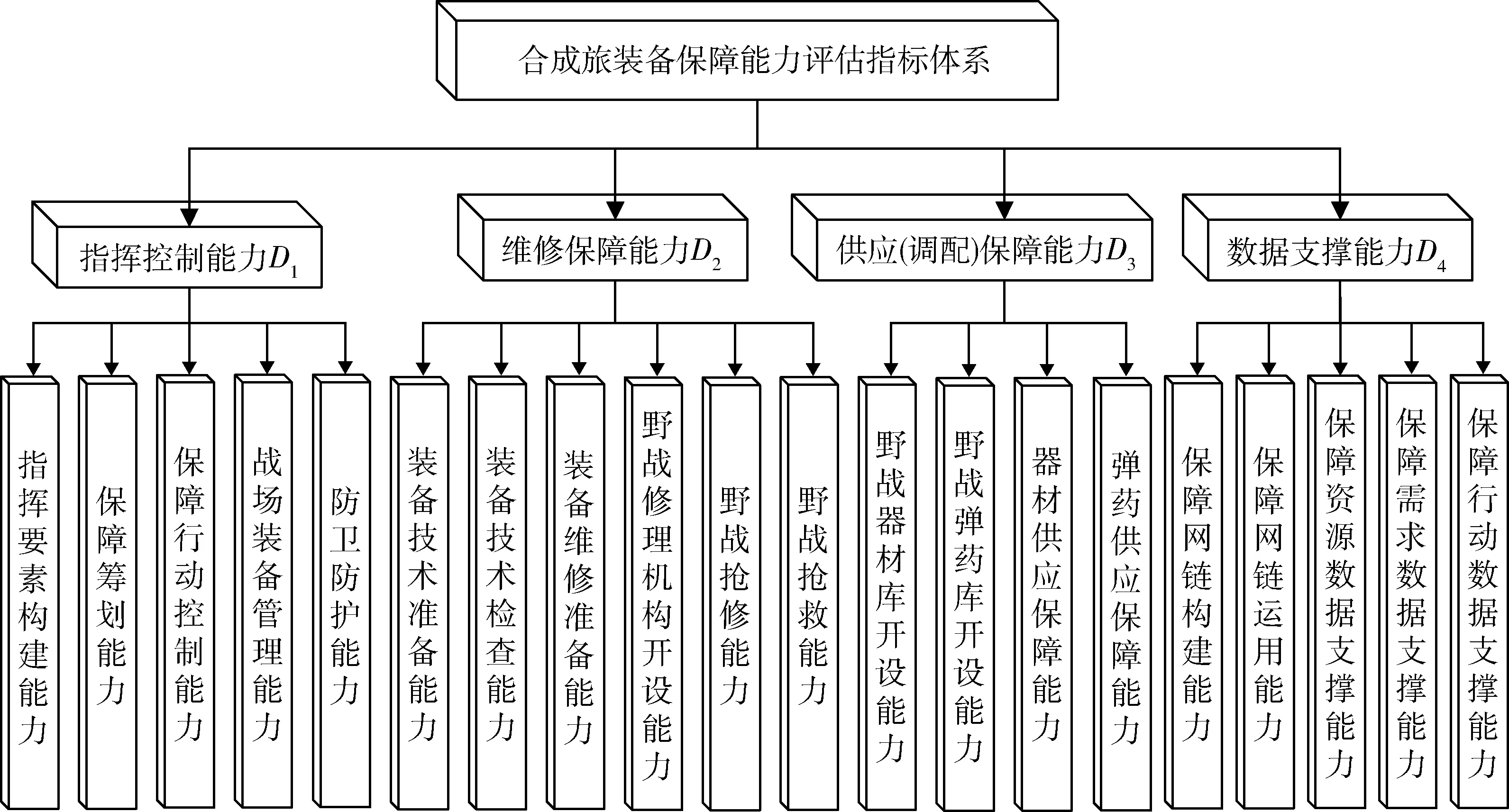
图2 合成旅装备保障能力评估指标体系Fig. 2 Composite brigade equipment support capability evaluation index system
2 指标权重的确定
为了更加科学地反映各指标对评价目标的作用,本文采用层次分析法与熵权法结合的综合赋权法计算评估指标的权重。
2.1 主观权重的确定
层次分析法是通过对相同层次内评估指标的两两比较,并计算其最大特征根来确定指标权重的主观确权方法,能够较好地反映评估组织者的主观意图。其具体步骤如下[9]:
(1) 构造判断矩阵
采用1-9 标度法定义判断
式中:aij为元素i 与元素j 的重要性之比。
(2) 计算最大特征根及其向量
1) 将判断矩阵的每一列正规化,即
2) 将判断矩阵按行求和,即
所得向量w'= (w'1,w'2,…,w'n)T即为所求特征向量。
4) 最大特征根为
式中:(Bw')i为向量Bw'的第i 个元素。
(3) 判断矩阵的一致性检验。
1) 一致性指标CI,定义为
当CI= 0 时,lmax=n,判断矩阵具有完全一致性。
2) 平均随机一致性指标RI,其数值由表1给出。

表1 一致性指标值Table 1 Consistency index values
3) 随机一致性指标CR,定义为
一致性检验一般要求CR<0.10。如果一致性指标不满足要求,则需要调整判断矩阵中各指标间关系值,使其能够通过一致性检验,而后生成的特征向量w'为该层次相关指标的权重。
2.2 客观权重的确定[10]
熵权法是利用各评估指标的熵值来确定其权重的方法,其具体步骤为
设评估对象集为{Ai}(i= 1,2,…,m),指标集记为{Xj}(j= 1,2,…,n),xij表示第i个评估对象的第j个指标的原始值。
(1) 计算第j个指标下第i个评价对象的标准值:
(2) 计算第j个指标的熵值ej:
(3) 计算第j个指标权重αj:
2.3 确定综合权重
计算出主观权重与客观权重后,再进行综合赋权,其公式为
式中:wi为主观权重;αi为客观权重;λ为偏好系数,反映决策者或专家偏向主观还是客观。本文认为主客观权重地位同样重要,取λ= 0.5。
3 可拓云理论概述
3.1 可拓云模型基本原理
物元可拓模型是用名称、特征及指标值3 个元素来描述事物并建立物元模型,即R= (M,D,X),在确定经典域与节域基础上,通过指标关联度表示各元素和集合的关系、综合关联度表示待评物元的评价等级,多用于解决复杂不相容问题,适合多元素评价[11]。
云模型是将事物的模糊性和随机性相结合,通过数学表达式对不确定性问题进行定量描述的模型[12]。云模型中标准正态云应用广泛,其通过三元组(Ex,En,He)来表示。其中,期望Ex为隶属云的中心值;熵En是对属性概念的不确定表述,反映了模糊性和随机性;超熵He表示熵的不确定性,反映了样本的随机性。
可拓云评估方法是通过利用云模型的三元组(Ex,En,He)来代替物元分析法中待评事物的指标值X,从而减少X值的随机性,提高量值精准性的方法,其实现了对物元模型的改进[13]。该模型可表示为
式中:R为合成旅装备保障能力评估的等级;Di为评价指标;(Ex,En,He)为评价指标Di关于等级的云描述。
3.2 可拓云模型的计算步骤[14]
结合合成旅装备保障能力评估实际,可拓云模型的计算步骤具体如下:
(1) 确定待评物元
评估的对象为合成旅建制内装备保障力量,待评物元为合成旅装备保障能力,则合成旅装备保障能力可拓云矩阵为
(2) 确定待评物元评估等级及其标准云
首先,本文确定合成旅装备保障能力评估等级为4 个级别:Ⅰ,Ⅱ,Ⅲ,Ⅳ,即优、良、中、差4 个等级。各评估指标的值域转换为百分制,各指标等级 标 准 区 间 值 设 定 为(80,100],(60,80],(35,60],(0,35]。
其次,将各评估指标的等级标准区间看作一个双约束空间(35,60]处理,综合考虑约束指标数值的模糊性和随机性,进行适度扩展后计算正态云模型的特征值
式中:S为常数,可根据评估指标的具体情况进行调整,本文设其为常数0.1。
最后,可求得各评估指标的等级标准云模型,见表2。
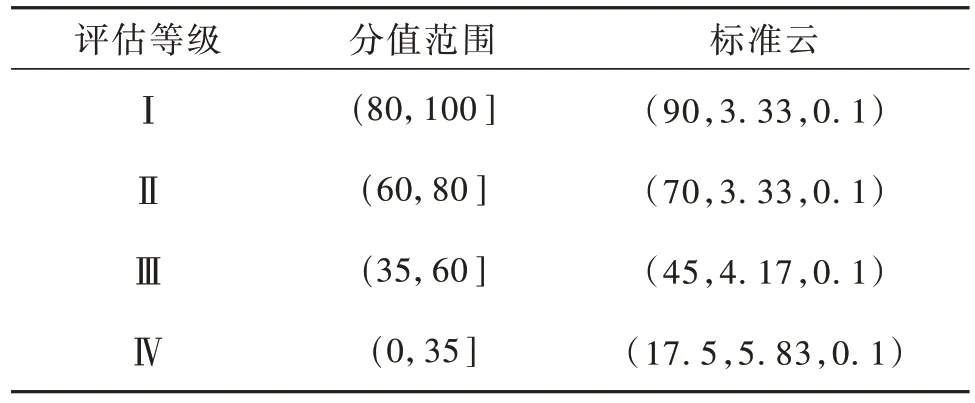
表2 评估等级及标准云Table 2 Evaluation grade and standard cloud
通过Matlab 编程,运行后得到各评估指标等级标准云图[15],如图3 所示。
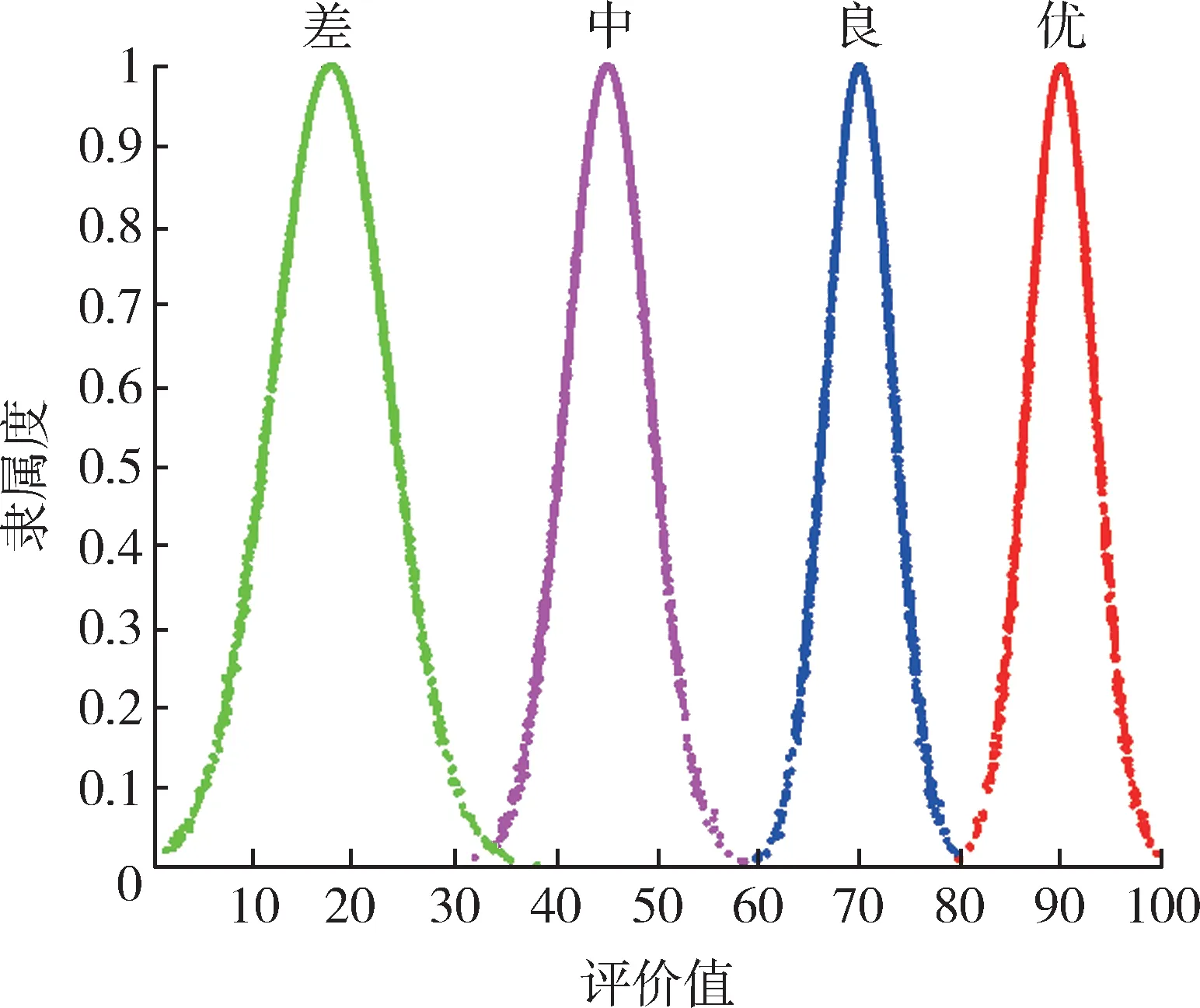
图3 评估指标等级标准云图Fig. 3 Cloud map of evaluation index grade standard
(3) 计算云关联度
首先,设评估指标的值为xi,则其云滴为(xi,ki),而后计算 其正态期 望值En、标准 差He的服从正态分布的随机数E'n,最后云关联度ki的计算公式为
设单个指标云关联度计算结果为kij,则所有评估指标的云关联度的综合评判矩阵K为
式中:kij为单个评估指标的云关联度;n为评估指标个数,本文为20。
(4) 计算装备保障能力评估结果及置信度
首先,计算综合评判向量B为
式中:W为综合权重向量;K为综合评判矩阵。
其次,计算综合评判分数r为
式中:bi为B对应的分量;fi为等级i对应的分值,本文设定合成旅装备保障能力评估等级为Ⅰ~Ⅳ级,各等级对应的分数依次取1,2,3,4。
需要强调的是,由于在求解云关联度k的过程中,E'n是服从正态分布的随机数,因此其计算结果存在随机性,故需要迭代运算以减少随机因素的影响。综合评判分数ri(x)的期望值和熵值为
式中:h为运算次数,本文取1 500;ri(x)为第i次运算得出的综合评判分数。
模糊等级特征期望值Ex,r最能代表合成旅装备保障能力评估等级的评估分数,通过将其与Ⅰ~Ⅳ级对应的分值对比,可确定最终的评估等级。
模糊等级特征熵值En,r能够衡量评估结果的离散程度。熵值越小,评估结果越集中,也就越可靠。可通过计算置信度因子θ确定可信度,即
经计算,置信度因子θ值越小,则评估结果越集中,可信度就越高;反之,则评估结果可信度就越低。
4 实例分析
4.1 确定待评物元
引入往年参加实战化装备保障综合演练评估的4 个 中 型 合 成 旅(分 别 记 为H1,H2,H3,H4)的 相关数据进行评估模型方法的分析验证。邀请10名专家对相关数据进行分析研究,给出对应评估指标值,算数平均后,得到评估指标值,如表3所示。

表3 评估指标值Table 3 Evaluation index values
4.2 指标权重和云关联度计算
(1) 计算评估指标权重
由于篇幅有限,仅以H1为例进行计算,通过式(1)~(11),可得各评估指标权重值,具体如表4所示。
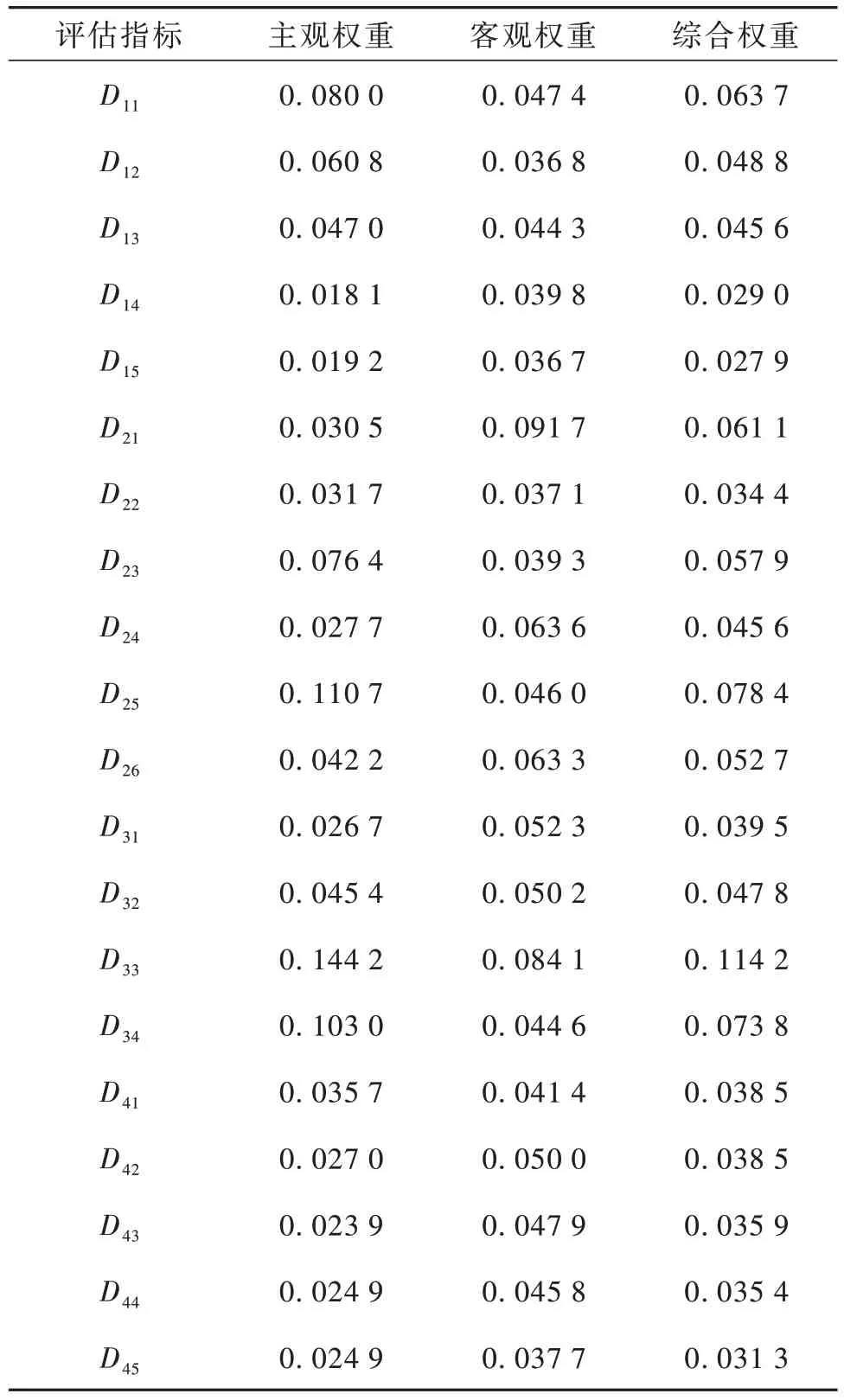
表4 评估指标权重值Table 4 Weight values of evaluation indicators
将评估指标的主观、客观及综合权重值进行对比,如图4 所示。部分指标的主、客观权重值之间存在一定的差异,进行综合赋权后,能较好地将主客观权重组合融合[16]。
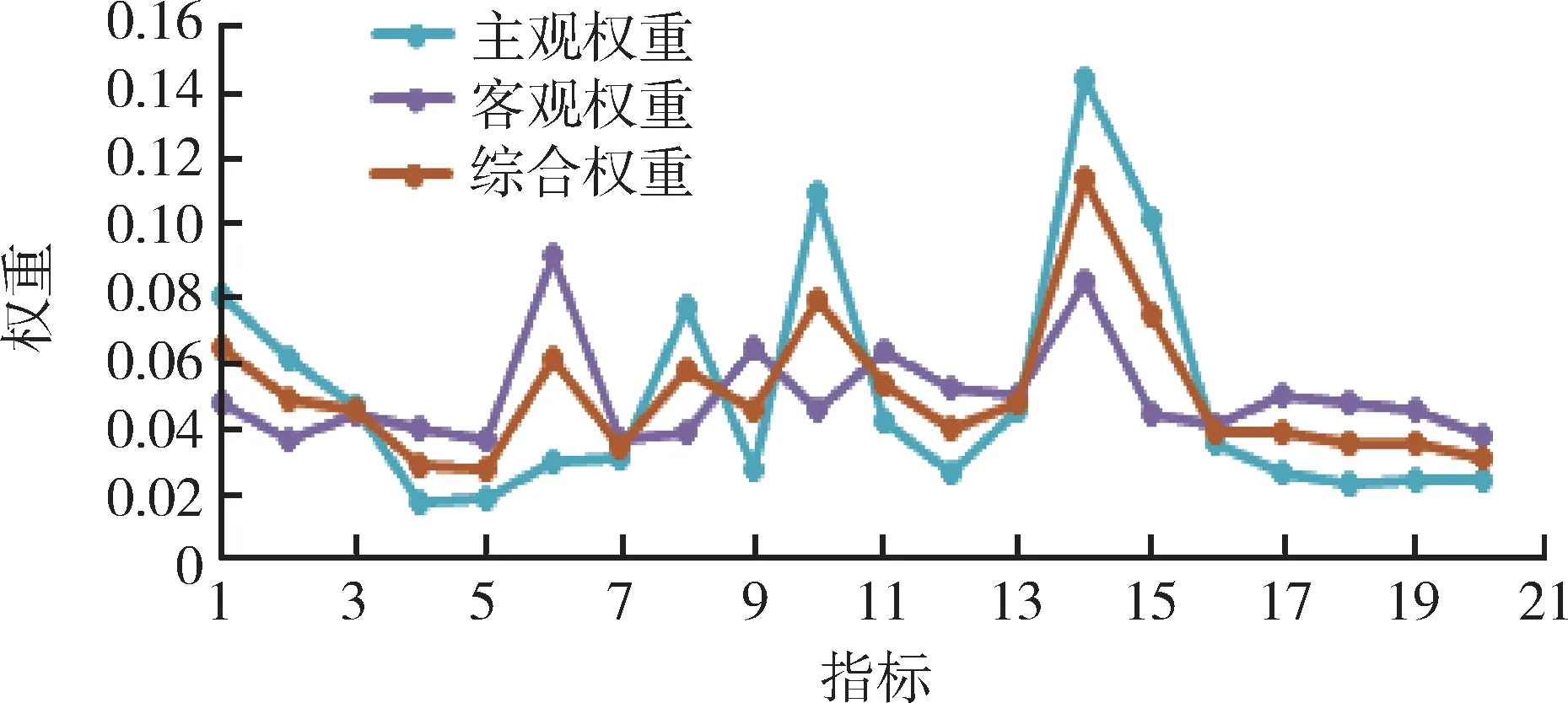
图4 指标权重对比Fig. 4 Comparison of index weights
(2) 计算评估指标云关联度
由于篇幅有限,仅以H1为例进行计算,根据式(12)~(17),可 得H1的 云 关 联 度,具 体 如 表5所示。

表5 H1 云关联度计算结果Table 5 Calculation results of cloud correlation degree
通过Matlab 编程,运行后得到H1云关联度云图,如图5 所示。
根据式(18)可得H1综合评判矩阵
4.3 评估等级及置信度确定
根据式(19)可得综合评判向量B=(0.003 7,0.267 9,0.046 3,0),综 合 评 判 分 数r=2.133 949。
根据式(20)~(25)可得Ex,r= 2.136 072,En,r=0.005 140,θ= 0.002 406,其评估等级为Ⅱ级。
同理,可得H2,H3,H43 个单位装备保障能力评估综合关联度和评估等级,如表6 所示。
根据表6 可生成4 个被评估单位评估结果云图,如图6 所示。期望值Ex,r代表被评估单位最终评估等级,H1评估结果为Ⅱ级,H2评估结果为Ⅱ级,H3评估结果为Ⅰ级,H4评估结果为Ⅱ级,4 个中型合成旅的装备保障能力都在Ⅱ级中等以上,装备保障能力较强。另外,通过置信度因子的计算,能够验证评估结果的可靠性,本研究中,4 个合成旅评估结果的置信度因子均小于0.02,表明评估结果较为可靠,验证了可拓云评估模型的有效性和合理性。
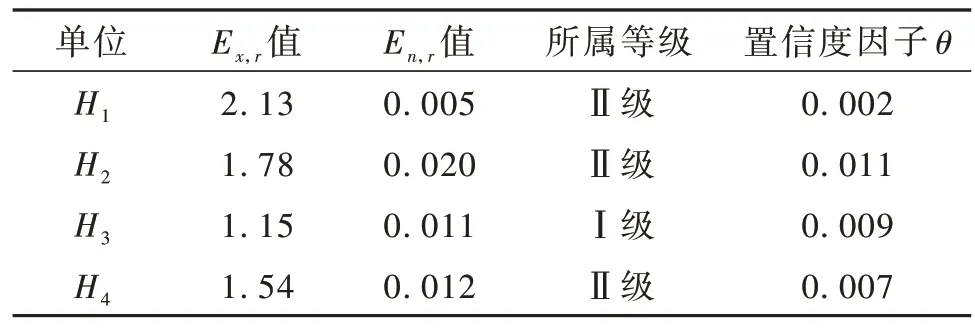
表6 综合关联度及所属等级Table 6 Comprehensive correlation degree and its grade

图6 评估结果云图Fig. 6 Cloud image of evaluation results
5 结束语
本文结合物元可拓模型与云模型的特点,通过构建可拓云模型实现对合成旅装备保障能力的评估。首先,基于合成旅装备保障任务,通过任务能力分解,构建了评估指标体系;其次,为增强指标权重的可信度,基于层次分析法与熵权法相结合的方法,综合确定评估指标的权重;然后,采用可拓云评估方法对合成旅装备保障能力评估中的模糊性和随机性问题进行处理,构建了基于可拓云的合成旅装备保障能力评估模型;最后,通过对4 个中型合成旅装备保障能力进行评价,验证了该评估模型的有效性,取得了较好的效果。通过研究,该方法能够对合成旅装备保障能力作出更加科学有效的评估,能够为合成旅装备保障能力评估实践提供理论支撑。
