基于核心素养理念的初中数学教学探究

车林林

摘要：目前初中数学教学存在缺乏与生活的联系、缺乏实际问题的应用、数学文化融入少等问题。在数学教学中，教师要基于以上问题，积极优化教学方法，引导学生实现从感性思维到理性思维的转变，实现数学学习效率的提升。文章重点探究基于核心素养理念的初中数学教学策略：联系现实生活，培养数据分析能力；引进实际问题，培养数学运算能力；融入数学文化，培养数学抽象能力；创设教学情境，培养直观想象能力；设计提问方案，培养逻辑思维能力。

关键词：初中数学；核心素养；数据分析；数学运算；数学文化；逻辑思维

中图分类号：G633.6文献标志码：A文章编号：1008-3561（2023）05-0085-04

基于素质教育要求，如何实现教学与核心素养培养的融合，发展学生的核心能力，是初中数学课堂教学改革的方向。在传统数学教学中，部分教师更注重学生对数学解题技巧的掌握和应用、数学知识的理解和分数的提升，并不注重培养学生的数学学习兴趣，也不关注其能否应用数学知识解决实际问题。在数学核心素养培养背景下，教师要走出机械灌输的误区，关注学生的能力培养，让其在实践中不断提高数学应用能力，为进阶高难度数学学习和实践应用奠定基础。

一、培养学生数学核心素养的意义

数学核心素养包括数學建模、逻辑推理、数学抽象、数据分析、直观想象等，是新课程改革的重点内容，也是数学学科教学改革的主要方向。在数学教学中，教师要充分落实核心素养培养理念，积极促进学生的综合能力发展，使其成为具备必备品质与关键能力的综合型人才。数学核心素养的培养途径包括数学课堂和现实生活。让学生通过社会生产实践总结数学学习方法，将学得的知识、技巧应用于生活中，可不断提高学生的数学学习能力和应用能力。

二、初中数学教学存在的问题

1.缺乏与生活的联系

数学是一门研究数量关系和空间形式的学科，是社会生产、实际生活不可缺少的工具。在以往教学中，部分教师过于关注数学技巧、理论知识的灌输，迫切希望提高学生的数学分数，忽视教学与生活之间的联系，忽略培养学生的数学思维、解决问题等能力，从而阻碍了学生综合能力的发展。同时受“应试教育”思维影响，部分教师存在采用习题来锻炼学生的知识应用能力等情况，导致数学学习与生活脱节。这样，学生就缺乏结合自己的生活经验和阅历理解知识、解决问题的意识与能力。

2.缺乏实际问题的应用

解决数学问题是初中数学教学的重要环节，也是培养学生数学核心素养的主要途径，但从目前的教学情况看，部分数学教师课堂设置的问题多围绕考试进行，以帮助学生更好地应对和解决考试中的问题，而这无法激活学生的思维，打开学生的解题思路，导致学生的数学思维没有得到真正锻炼。此外，部分教师以是非的方式进行提问，这无法使学生调动已有的知识和生活经验对问题进行深入思考。

3.数学文化融入少

缺少数学文化的融入是课堂教学存在的问题之一。有的教师只关注教材上的知识点，忽略数学文化的应用，有的教师未充分认识到融入数学文化的作用和应用意义，认为没有必要，通过创设教学情境，如分享数学趣事也能突出一定的数学思想。其实，数学文化的内涵十分广泛，包括数学家探索历程、数学发展史、数学美学、数学人文活动等，单纯靠数学故事不能让学生了解其背后蕴含的文化价值。

三、核心素养理念下初中数学教学策略

1.联系现实生活，培养数据分析能力

数据分析是指学生在获得相应数据后，采用统计方法，分析和推理其中的有用信息。初中数学涉及的概率、统计内容较少，部分教师通常根据教材内容，粗略地指导学生收集、整理和分析数据，导致学生的数据分析角度、方法单一，数据分析能力较弱。数据分析与现实生活息息相关，对此，教师应积极将课堂教学与现实生活相联系，引导学生从生活中收集、分析数据，感受数据分析的现实意义，并将数据分析应用于生活中，以提高数据分析能力。

例如，在“随机事件与概率”教学中，教师可以简单的生活事物，引导学生了解概率和随机事件的定义。在日常生活中，部分游戏规则或抽奖活动都采用了概率知识，为让学生学会将数学知识应用于现实生活中，教师可引导学生用概率判断游戏或抽奖活动是否可行。如以下抽奖活动：在元旦联欢晚会上，学校举办了抽奖游戏环节，由每个班级的一名代表转动转盘，当指针指向转盘上的奖励项目后，即可获得相应的奖励。圆形转盘分为7个面积相等的扇形，每个扇形都贴有相应的奖项名称，如一等奖、二等奖、三等奖、鼓励奖、参与奖、谢谢参与、惩罚。每个人只能转2次。学生进行分组讨论，分析转盘指针指向哪个奖项的可能性更大。有的学生设计了表格，列出第一次转动转盘的所有可能性和第二次转动转盘的所有可能性，学校共有12个班级，列出12个班级的第一次和第二次转动转盘的结果。在制作表格的过程中，学生能掌握主要数据的收集、整理、提取方法，并通过整理出来的数据，分析抽中一等奖事件的可能性。由此可见，联系实际生活可让学生以自主探究的形式分析数学数据，将生活问题转化为数学问题，掌握数据收集、整理、分析的方法，从而实现数据分析能力的提升。

又如，在“用频率估计概率”教学中，教师也可通过联系生活，引导学生分析数据，体验数学知识在社会生活中的重要性：学校要种植某种幼树，采用什么方法，才能保证幼树移植的成活率？幼树移植成活是一种概率，其成活与不成活两种结果是否相等尚未可知，可采用频率去估计。根据问题可知，移植的数目越大，频率越不稳定，因此可将移植数目设为n，成活数目设为m，成活的频率则为m/n，然后根据这个频率设定n、m值，尝试算出最大的概率。教师通过鼓励学生发现、研究现实生活中的问题，可使学生进行积极思考，充分将数据分析应用于现实生活中，实现数据分析能力的提升。

2.引进实际问题，培养数学运算能力

数学运算包括运算方法、运算对象、运算原理和运算关系等，数学运算能力是学生的数学基本功，也是数学核心素养的内容之一。因此，在初中数学教学中，教师要重视数学运算训练，但训练方法不合理、训练量过大，会影响学生对数学运算的理解，不利于其数学核心素养的发展。在数学核心素养培养背景下，教师应寻求更有效的教学方法引导学生进行运算训练，如应用实际问题可使学生理解运算对象，根据运算法则解决数学问题，从而不断丰富运算思路、方法和经验，还能锻炼学生的数学思维，提升学生学以致用的意识。对此，教师要了解实际问题在教材中的占比，并对教材上的问题进行创新，尝试将数学问题与实际问题进行转化，使学生更好进行实际问题的运算训练，不断提升数学核心素养。

例如，在“解一元二次方程”的教学中，学生要从一元二次方程的简单求根入手，计算一般形式下的根，学会用配方法求解一元二次方程的根，并将一般形式配方成（x-n）2=p形式。首先，教师可设计如下常见的实际问题：农夫想用一段长为20m的铁丝围成一个24m2的矩形，请同学们帮农夫想一想要怎样围。以此引导学生在解决问题的过程中体会一元二次方程的意义和特点。九年级学生已经会列方程式，当出现未知数时，通常将其设为x，根据矩形周长为20m，面积为24m2，于是将长设为xm，宽为（10-x）m，根据面积公式列出x（10-x）=24，整理成一般形式：-x2+10x-24=0。然后，教师可引入新知，让学生说出熟悉的、容易解的一元二次方程，如x2=4、x2=9等，并参照x2=9的解法，求解（x+2）2=9，即引导学生建立由一元二次方程转化为一元一次方程、未知转化为已知的运算思维。可见，引进实际问题可加深学生对知识的理解，实现学生数学运算能力的提升。

3.融入数学文化，培养数学抽象能力

数学不仅具有抽象性，还具有人文性。教师若能从数学文化的角度开展教学，不仅能激发学生的学习兴趣，还能锻煉其想象力，帮助其更好地理解抽象的数学知识。而教师要想将数学文化有效融入教学中，就不能单纯引用课本上的数学文化，还要熟悉数学史，关注更多的数学文化。例如，在教学某章节的知识时，教师可先普及该知识点的来源和发展史，再讲数学家总结的数学思想。这样，学生不仅能感受到知识点对应的教学目标和文化背景，还能丰富课堂体验，产生浓厚的学习兴趣，并能联想知识点的形成过程，提升数学抽象思维能力。

例如，在“圆的有关性质”教学中，由于圆的相关概念和形式都比较抽象，学生理解起来有一定困难。因此，教师可借助数学文化，让学生了解圆的相关知识的发现、发展史，让其逐渐理解和内化知识。首先，教师可向学生讲解圆的定义：一条线段绕着它的一个端点在平面内旋转一周，它的另一个端点的轨迹叫作圆。然后，教师可用PPT展示圆的相关知识的发展史，尤其是圆周率的提出，如向学生介绍阿基米德是如何求出圆周率的。古希腊数学家阿基米德用外切正多边形和圆内接的方法，使用迭代计算和两侧数值逼近，从正六边形开始，逐渐加倍运算到正九十六边形，取其近似值，即3.141851为圆周率的近似值。之后，有数学家用“割圆术”进一步计算出圆周率的数值在3.1415926与3.1415927之间。2019年3月，谷歌公司的工程师爱玛在谷歌云平台的帮助下，将圆周率计算到小数点后31.4万亿位。在以上这些内容的基础上，教师可引导学生尝试采用阿基米德计算方法和“割圆术”，算出圆周率数值。数学文化的融入可让学生经历圆的认识过程，进而从不同层面掌握圆的定义和性质，实现数学知识的高效学习，并树立文化自信。

4.创设教学情境，培养直观想象能力

直观想象能力包括利用图形分析数学问题、借助空间感知事物形态变化及运动规律、建立数与形的联系等，是指学生借助空间想象或几何图形直观感知事物的变化，并运用图形解决问题的能力。在传统数学教学中，部分教师直接采用教具或图片来展示事物的形态变化、运动规律及建立数与形的关系，讲解空间几何知识，忽略培养学生的直观想象能力。而创设演示、故事等教学情境可调动学生的学习积极性，培养学生的数学学习能力。在教学中，教师可以选择游戏情境、演示情境引导学生从直观平面模型想象出空间立体模型，从而实现直观想象能力的提升。

例如，在教学“图形的旋转”这部分内容时，教师可以创设“我是小老师”的演示情境，让学生上台操作和演示，并向其他同学分享自己的实践成果，以此吸引学生参与课堂教学活动。在创设情境前，教师要确保学生充分理解旋转的要素，包括中心点、方向和角度，然后让学生在台下预先演示。在预演时，学生可用学具模拟旋转过程，从而在脑海中形成清晰的动态影像，并归纳总结图形旋转的性质，确定图形旋转后的位置、大小，画出旋转后的图像。“小老师”上台后，用一个手指按住三角形卡片和小棒的中心点旋转180°，然后让台下的同学说出图形旋转后发生了什么改变。有的学生发现旋转后的图形与原来的图形全等，也有学生发现对应点到旋转中心的距离相等。创设演示情境可让学生以实践操作来感知知识的形成过程，为其想象图形旋转提供了表象基础，还可逐渐加深学生对图形旋转本质的认识，即由原来的模糊经验变成系统、清晰、抽象概括的数学认知。

5.设计提问方案，培养逻辑思维能力

逻辑思维能力是学生应具备的数学学习能力，也是数学核心素养的内容之一，而提问是启发学生思维的重要手段。基于数学核心素养的培养要求，教师可设计循序渐进的提问方案，引导学生通过解答问题，发现问题解决的不同途径，从而实现逻辑思维能力的提升。在课堂教学中，教师还可根据学生的学习水平、认知水平等设计问题，从多方面、多角度提出富有思想性、启发性的问题，科学地引导学生思考、探究和分析，以提高学生的逻辑思维能力。

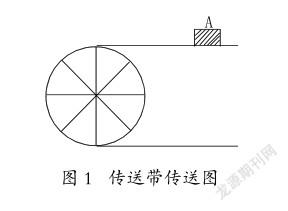
例如，在教学“弧长和扇形面积”时，学生已经学习了圆的周长、面积等知识，而弧长、扇形与圆息息相关，教师若想引导学生深入理解新知识，就要设计新旧知识的衔接问题，即由已学知识引出新知识。首先，设计问题：圆的周长如何计算？圆的面积如何计算？圆的圆心角是多少度？同学们剪下一个圆，并折一折，找出弧长、扇形与圆之间的关联。这种方法是借助问题引导学生理解弧长的概念。然后继续提出问题，引导学生探索弧长公式：如图1，某传送带的转动轮半径为a厘米，若转动轮转一周，传送带上的物品被传送多少厘米？若转动轮转了1°，传送带上的物品被传送多少厘米？若转动轮转n°，传送带上的物品被传送多少厘米？

在此基础上，教师可引导学生推算半径为R的圆中，n°的圆心角所对的弧长计算公式。学生从已知条件中得知半径为R，圆心角为n°，并且已知弧长是圆上过两点的一段弧的长度，与圆心角、半径相关，从而推导出弧长的计算公式為L=n仔r/180。由此，教师通过提出循序渐进的问题，引导学生抽丝剥茧地解决问题，可启发学生的逻辑思维，促进学生数学核心素养的提升。

基于数学核心素养的培养要求，教师设置的问题要结合学生的认知特点，做好问题的结构与衔接设计工作，还要确保问题的发散性和开放性，从而使学生的逻辑思维得到有效启发和锻炼。以“反比例函数”教学为例，教师可设计三个开放性问题，让学生在轻松的氛围中大胆思考和猜想问题中的变量关系，以此引出反比例函数的表达形式。（1）京沪铁路全程1463千米，乘坐列车所用时间t小时随着该列车的平均速度v千米/小时的变化而变化，请问其中的变量关系如何用函数关系式表示？（2）某小区要种植1850平方米的矩形草坪，草坪的长度y随着宽度x变化而变化，如何用函数关系式表示？（3）已知本市总面积为1.68×10⁵平方千米，人均占有土地面积s随本市人口n的变化而变化，如何用函数关系式表示？在解答上述问题时，学生可以采用多种形式表达两个变量关系，但最终发现两个变量均为反比例关系，从而引出反比例函数关系式。教师还可鼓励学生以身边的事物来设计反比例函数关系式，有的学生举出例子：矩形面积为20平方厘米，相邻的两条边长为x和y，反比例函数关系式为y=20/x。教师可让其他学生判断其是否属于反比例函数。可见，发散性问题可让学生充分利用自己积累的知识和经验，挖掘和推理出问题中变量的变化规律与关系，并逐渐形成概念，以此提升逻辑思维能力。

四、结语

总而言之，初中数学教师若想有效开展数学核心素养培养，就要将教学重点聚焦在学生的能力培养上，创新和优化教学方法，从教学中的不足和现存问题出发，针对性选择教学策略，如联系现实生活、引进实际问题、融入数学文化、创设教学情境、设计提问方案等。这样，可充分培养学生的数据分析能力、数学运算能力、数学抽象能力、直观想象能力、逻辑思维能力等数学核心素养。

参考文献：

[1]贾小利.浅析核心素养理念下初中数学有效教学情境的创设[J].甘肃教育研究，2022（09）.

[2]邹世德.核心素养培养理念下初中数学教学策略[J].数理化解题研究，2022（26）.

[3]薛珂.核心素养理念下初中数学教学探究[J].中学数学，2022（18）.

[4]巫锦娟.基于数学核心素养理念的初中数学课堂教学策略[J].数学大世界，2021（11）.

[5]韩燕.核心素养培养理念下初中数学教学对策研究[J].天津教育， 2021（27）.

[6]黄金松.浅谈基于核心素养理念的初中数学教学[J].中学数学教学参考，2021（21）.

[7]陈爱珠.数学核心素养理念下的初中数学课堂教学研究[J].数学学习与研究，2021（04）.

[8]顾启焕.核心素养理念下的初中数学课堂教学[J].数学大世界， 2020（07）.

Exploration of Mathematics Teaching in Junior Middle School Based on the Concept of Core Competence

Che Linlin

（Wafangdian No. 7 Junior Middle School， Liaoning Province， Wafangdian 116300， China）

Abstract： At present， there are some problems in junior middle school mathematics teaching， such as the lack of connection with life， the lack of application of practical problems， and the lack of integration of mathematical culture. In mathematics teaching， teachers should actively optimize teaching methods based on the above problems， guide students to realize the transformation from perceptual thinking to rational thinking， and improve the efficiency of mathematics learning. The article focuses on exploring the teaching strategies of junior middle school mathematics based on the concept of core competence： connecting with real life， cultivating the ability of data analysis； introduce practical problems and cultivate mathematical operation ability； integrate mathematical culture and cultivate mathematical abstract ability； create teaching situations and cultivate the ability of visualization and imagination； design the questioning plan and cultivate the logical thinking ability.

Key words： junior middleschoolmathematics； core competence； data analysis； mathematical operation； mathematics culture； logicalthinking