低成本制导弹药虚拟运动预测组合导航方法

纪 毅，李浩天,2，范军芳,2，刘 宁,2，马乾才

（1.北京信息科技大学 自动化学院，北京 100192；2.高动态导航技术北京市重点实验室，北京 100192；3.西安现代控制技术研究所，西安 710065）

因其兼具高精度、低成本与“打了不管”的特点，卫星制导弹药被广泛应用于实战。然而，其自身强耦合力学特性与多变形飞行方案对卫星信号接收带来干扰，在其飞行过程中，卫星信号延迟、闪烁、衰减甚至丢失的现象时有发生，严重降低了该类制导弹药的制导精度，削弱其精确毁伤能力，甚至引发脱靶。鉴于此，捷联惯性导航系统（Strapdown Inertial Navigation System,SINS）被引入卫星制导弹药。SINS系统具有全天候自主工作、扰抗性与隐蔽性强的优势，但其误差会随时间积累。全球定位系统（Global Positioning System,GPS）与SINS 系统具有优劣互补的特性，因而SINS/GPS 组合导航系统被广泛应用于精确制导弹药中[1]。

利用SINS 系统测量的运动信号补偿缺失的卫星导航信号，不失为一种解决卫导信号缺失条件下精确导航问题的有效手段。但当卫星信号缺失时，低成本制导弹药将转入低精度SINS 系统独立工作的状态，其角速率陀螺和加速度计的惯性误差随时间快速发散，难以保证导航精度。近年来，随着计算机算力的提升，基于神经网络和人工智能（Artificial Intelligence,AI）的SINS/GPS 组合导航方法[2-5]广受关注。该方法在GPS 有效时训练组合导航模型，当GPS 失效时，利用训练好的导航模型对SINS 系统误差加以校正，进而解决卫导信号缺失条件下精确导航问题。然而，基于AI 的组合导航算法虽具有良好的应用前景，但需要大量导航数据做依托，计算量大，实现过程复杂，处理速度慢，迁移性差，现阶段难以实时在线应用。

目前，卡尔曼滤波（Kalman Filtering,KF）仍是实现组合导航系统数据融合的主要手段。KF 是一种递推式最小方差估计方法，具有估计精度高和计算量小的特性，易于计算机实现，被广泛应用于多源信息融合系统[6]与组合导航系统[7,8]之中。KF 的估计精度和状态收敛速度取决于过程噪声与量测噪声的统计学精度，即噪声协方差矩阵的选取。为选取合适的滤波参数，徐晓苏等[9]使用粒子群算法对KF 的滤波参数进行寻优，提升了滤波算法的估计精度；曾庆化等[10]构建了基于指数函数的动态遗忘因子模型，提出了基于指数渐消遗忘因子的自适应滤波算法；Hu 等[11]基于极大似然理论提出了一种扰动抑制自适应无迹KF，可在线估测与更新噪声方差。近年来，基于KF 的组合导航技术被广泛应用于以战略、战术导弹为代表的制导弹药中。孙照强等[12]基于弹道方程将扩展卡尔曼滤波(Extended Kalman Filter,EKF)应用于地面跟踪雷达的场景中，Liu 等[13]提出一种改进型的容积KF 应用于组合导航的导弹姿态测定中。刘英等[14]提出了一种基于新型自适应联邦KF 的巡航导弹组合导航方法，提升战术导弹多源传感器的容错性。

在以上工作中，导航信息主要取信于弹载高精度惯导系统，在长期导航过程中通过GPS 辅助修正惯导系统误差。然而，以短程空地制导弹药、制导炮弹、制导火箭弹为代表的一类低成本制导弹药仍采用廉价的微电机系统(Micro-Electro-Mechanical System，MEMS)捷联惯导元件，相对而言，精度低、漂移大。本文面向SINS/GPS 松组合导航体制的低成本制导弹药，针对其制导过程中GPS 信号短时丢失条件下的精确导航问题，在不增加外部传感器的条件下，提出了一种基于虚拟运动状态预测的导航与制导方法，并利用一种基于新息序列协方差与理论协方差不匹配度的自适应卡尔曼滤波器(Adaptive Kalman Filter,AKF)实现非完备信息下的导航，有效提升组合导航系统对噪声中不确定性的容忍度，进而提升导航精度。虚拟运动预测适用对象射程在30-80 km 范围内的短程制导弹药，适用于除推进段以外的飞行全程，主要包括滑翔段与制导控制段，可以补偿10-15 s 以下的连续失效的卫星信号。以上阶段，制导弹药飞行轨迹与姿态仅受空气动力学与制导指令的影响，可实现精准预测。

1 组合导航基本原理与问题描述

1.1 SINS/GPS 松组合制导方案

SINS/GPS 松组合制导弹药的工作原理如图1所示。在弹药飞行制导过程中，SINS 系统与GPS 系统同时独立工作：IMU 模块实时测算姿态角速率与弹药加速度，并将其输入SINS 解算模块以计算位置、速度、姿态导航参数；GPS 接收机实时接收来自卫星的当前星历下的导航参数，并解算出位置与速度。通常，将以上两套系统的导航参数差值输入KF，并将滤波后的结果补偿至SINS 解算模块，得到更为可信的位置与速度信息，从而完成信息融合。可见，一定程度上KF 的性能直接影响了导航的精准性。

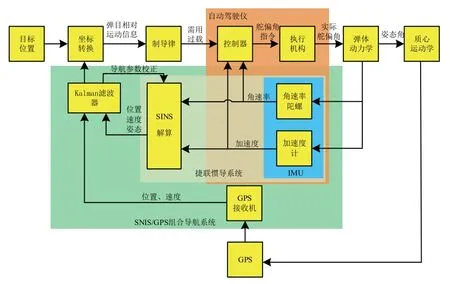
图1 SINS/GPS 松组合制导弹药工作原理Fig.1 Principles of missiles equipped with SINS/GPS system

上述位置与速度信息经坐标转换运算后生成弹目视线角速率信息，又经制导律运算后得到需用过载，并将其输入至自动驾驶仪。自动驾驶仪由控制器、执行机构（舵机）与IMU 模块组成，可计算弹体所需舵偏角指令，生成实际舵偏角，进而改变弹体飞行姿态，实现精确制导。

1.2 松组合制导弹药的状态方程与量测方程

SINS/GPS 松组合导航系统的滤波状态方程可表示为：

其中，A为松组合制导弹药系统的状态矩阵，G为噪声驱动矩阵，其表述形式详见文献[15]；X为松组合制导弹药系统的状态向量，W为系统过程噪声。X和W表达为如下向量形式：

式中，φ=[φE,φN,φU]为制导弹药在地理坐标系下的姿态角误差，δV=[δ VE,δVN,δVU]为制导弹药在地理坐标系下的速度误差，δL=[δ L,δλ,δh]为制导弹药的纬度、经度、高度误差，εb=[εbx,εby,εbz]和∇b=[∇bx,∇by,∇bz]分别为弹体坐标系下陀螺仪和加速度计的误差，ωg=[ωgx,ωgy,ωgz]和ωa=[ωax,ωay,ωaz]分别为弹体坐标系下陀螺仪和加速度计的过程噪声。上述各误差的动力学过程参照文献[15]。

当GPS 系统正常工作时，量测方程如下：

式中，Z为X的量测值矩阵，V为量测噪声，H为量测矩阵，表示为：

据此观测弹药在地理坐标系下的速度误差以及纬度、经度、高度误差。

由上述松组合导航基本工作原理及其状态、量测方程可知，SINS/GPS 松组合导航系统以卫星信息为基准，实时补偿SINS 系统，以消除IMU 惯性误差积累的影响，进而实现对载体姿态、位置与运动速度的有效量测。但当卫导信号缺失发生时，上述信息中惯性误差无法得到有效补偿，往往大幅度降低弹药的制导精度与毁伤效果。因而，对卫星信号缺失条件下的信息补偿制导的研究，具有重要的应用价值与现实意义。

2 基于虚拟运动状态预测的制导方法

2.1 卫星信号缺失条件下制导方法设计

本文从制导律出发，采用载体虚拟运动状态预测的方法，在卫星信号缺失条件下对SINS 导航参数进行补偿，其工作原理示意如图2所示。

图2 虚拟导航参数补偿原理Fig.2 The principle of virtual guidance parameters

图2 中SINS 和GPS 导航参数均来自弹上元件，无需单独设计。虚拟导航参数由卫导信号丢失后的一段时间内弹药运动状态预测得出，由起始时刻弹药运动状态与制导律决定。

2.2 考虑自动驾驶仪动力学的比例导引制导律

在三维空间环境条件下，将弹体与目标视为两个质点，弹目相对运动可在惯性笛卡尔坐标系O-XYZ中描述，如图3所示。图中M为弹体，T为目标，R为弹目相对距离，V为弹药速度；OA为弹药速度方向，OB为弹体纵轴方向，OC为弹目视线方向，平面OAB垂直于平面OBC；θM为弹体纵轴与弹药速度的夹角，ϕM为弹目视线与弹体纵轴的夹角，θM与ϕM的方向互相垂直；θL与ϕL分别为弹目视线角在惯性系下的垂直分量与水平分量。

图3 三维制导飞行过程示意图Fig.3 Three-dimensional homing engagement phase

据此，建立三维空间环境下制导动力学方程：

式中，ay和az分别表示弹药在偏航和俯仰方向的加速度。自动驾驶仪部分可视为如下二阶振荡动力学环节：

式中，a为偏航或俯仰通道的实际加速度，ac为对应通道的需用加速度指令，ξ为弹体阻尼，ω为弹体固有频率。

因其具有需求信息少、设计简单的特性，经典比例导引制导律(Proportional Navigation Guidance,PNG)被广泛应用于实际工程。三维条件下的PNG 可表述为：

其中，N为比例导引增益，和分别为制导弹药纵向和侧向的加速度指令。

考虑如式(5)所示自动驾驶仪动力学，应用滑模控制方法和反步法对式(6)制导律进行改进，改进后的PNG 为：

将式(8)代入式(5)，经坐标变换后，即可解得导航坐标下虚拟的位置与运动速度，其坐标转换矩阵如下：

式中，c（·）=cos（·），s（·）=sin（·），ψ=ϕL+ϕM为航向角，θ=θL+θM为俯仰角，横滚角γ= 0。

3 基于新息协方差不匹配度的AKF 设计

经典KF 视系统的过程噪声和量测噪声为白噪声，其收敛性取决于对噪声信号统计学特性的准确估计。然而在组合导航系统中，噪声的协方差矩阵往往是未知的，往往需要根据经验设计。考虑弹药的高动态特性，卫星信号叠加干扰、遮挡等不利的影响因素，导致接收机对多重因素所致的噪声强度估计准确度降低。上述问题可通过设计具有量测噪声协方差自我矫正功能的AKF 来解决。胡杰等[7]提出了实际新息协方差和理论协方差的不匹配度概念，设计了关于量测噪声的AKF，并成功应用于车载组合导航系统。该AKF基于模糊算法，通过构建输入与输出的隶属度函数与模糊度函数的关系来实现滤波器的收敛，一定程度上具有平滑性与容错性，但其难以跟踪具有高动态特性的弹药。受其启发，本文引入了新息协方差不匹配度的概念，在此基础上，根据弹体的特性对AKF 进行改进。

考虑SINS/GPS 松组合导航系统的状态方程(1)，经离散化处理后，其线性离散系统模型为：

其中，T为滤波周期。

对量测方程(3)离散化处理后，表示为：

根据以上系统方程与假设，设计基于新息协方差的AKF。文献[7]定义了新息协方差不匹配度均值的概念，如下：

其中，M为平滑窗口，Pk,k1-为KF 从第k-1 步到第k步的一步预测协方差。e为系统新息，由式(16)确定：

本文所述AKF 表示如下：

式中，μ＞0 为设计参数，sgmf函数表述为：

式中，ε＞ 0为待设计参数，本文令ε= 1。根据式(14)中AveDoMk的定义可知：当AveDoMk=1时，AKF 完美收敛；当AveDoMk＞ 1时，需增大协方差增益，反之亦然。式(18)所述自适应协方差增益调节器具有自动调节功能：当AveDoMk远离1 时，协方差增益绝对值迅速增大，实现KF 的快速调节；当AveDoMk逼近1 时，协方差增益绝对值变化幅度减小，最终使AveDoMk稳定至1。

4 仿真分析

本节设计仿真实验来验证卫星信号缺失环境下的基于虚拟运动状态预测的组合导航方法的有效性。仿真试验分为两部分，首先，基于某次飞行试验中GPS与SINS 数据，对比EKF 和所述AKF 的效果，以证明所述AKF 的有效性；其次，通过模拟卫星信号缺失环境下的末制导情景，验证本文方法的有效性。

4.1 基于新息协方差不匹配度的AKF 有效性验证

以某次飞行实验中取得的GPS 和SINS 数据为基础，验证所述AKF 的有效性。制导弹药的初始经纬高坐 标 为（2.1730rad,0.8294rad,0m），射 向 为ϕM=0.08726rad，射角为θM=1.5708rad，发射速度为V=500m/s。制导弹药上各部件的特征参数与噪声如表1所示。

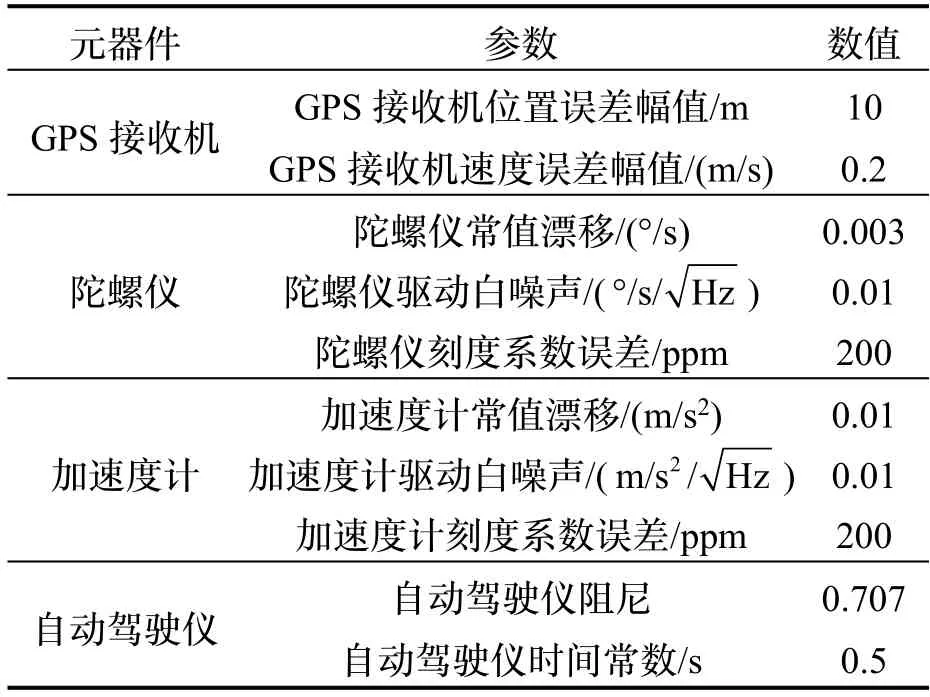
表1 弹上各部件的特征参数与噪声Tab.1 Parameters of sensors

根据表1 中陀螺仪和加速度计误差信息设计系统状态噪声矩阵W，根据GPS 接收机误差信息设计量测噪声矩阵V。此外，在所述AKF 中，设计参数为M= 20，μ= 5。

仿真结果如图4所示，包括GPS 系统和惯导系统数据，以及基于EKF 和AKF 的组合导航信息融合系统的仿真数据。图4(a)-(c)分别表示大地坐标系下的纬度、经度和高度数据信息，图4(d)-(f)分别表示以初始点为原点的地理坐标系下的东向、北向和天向位置数据信息，而图4(g)-(i)分别表示上述三个方向的速度数据信息。

图4 两种滤波器的仿真结果对比Fig.4 Comparison between EKF and AKF

上述仿真结果中，基于EKF 和AKF 的组合导航信息融合系统获取的信号值均在GPS 与SINS 系统之间，且数值相近，这验证了所述AKF 的有效性。因上述GPS 与SINS 数据源于实际飞行实验，每一时刻制导弹药的位置与速度真值无法获取，故本小节仅验证所述AKF 的有效性，不对其与EKF 的优劣进行评价。

4.2 基于虚拟运动状态预测的组合导航性能分析

本小节通过数学仿真实验验证基于虚拟运动状态预测的组合导航方法的有效性，分别模拟无GPS 信号丢失、GPS 信号断续以及GPS 信号随机丢失等三种情况，并从误差角度对所述AKF 与经典EKF 的效果与适应性进行分析。

仿真中，过程噪声和量测噪声均为高斯噪声，其中，过程噪声方差已知，量测噪声的初始方差取为真实值的0.1 倍。此外，考虑到随机风等环境影响，在制导弹药速度通道加入随机噪声。

在GPS 信号断续的仿真实验中，设前10 s 卫星信号正常接收，10 s-20 s 时间段卫星信号丢失，20 s 后卫星信号恢复。在GPS 信号随机丢失的仿真实验中，设置10 次GPS 信号随机丢失事件，每次信号丢失事件持续时间为0-1 s 内的随机数。

三种情况下的仿真结果分别如图5-7所示。各图中(a)为弹道曲线，(b)为位置误差(绝对值)，(c)为滤波器速度误差，(d)为AveDoMk和c值。对三种情况下的平均位置误差(绝对值)进行统计，结果如表2所示。

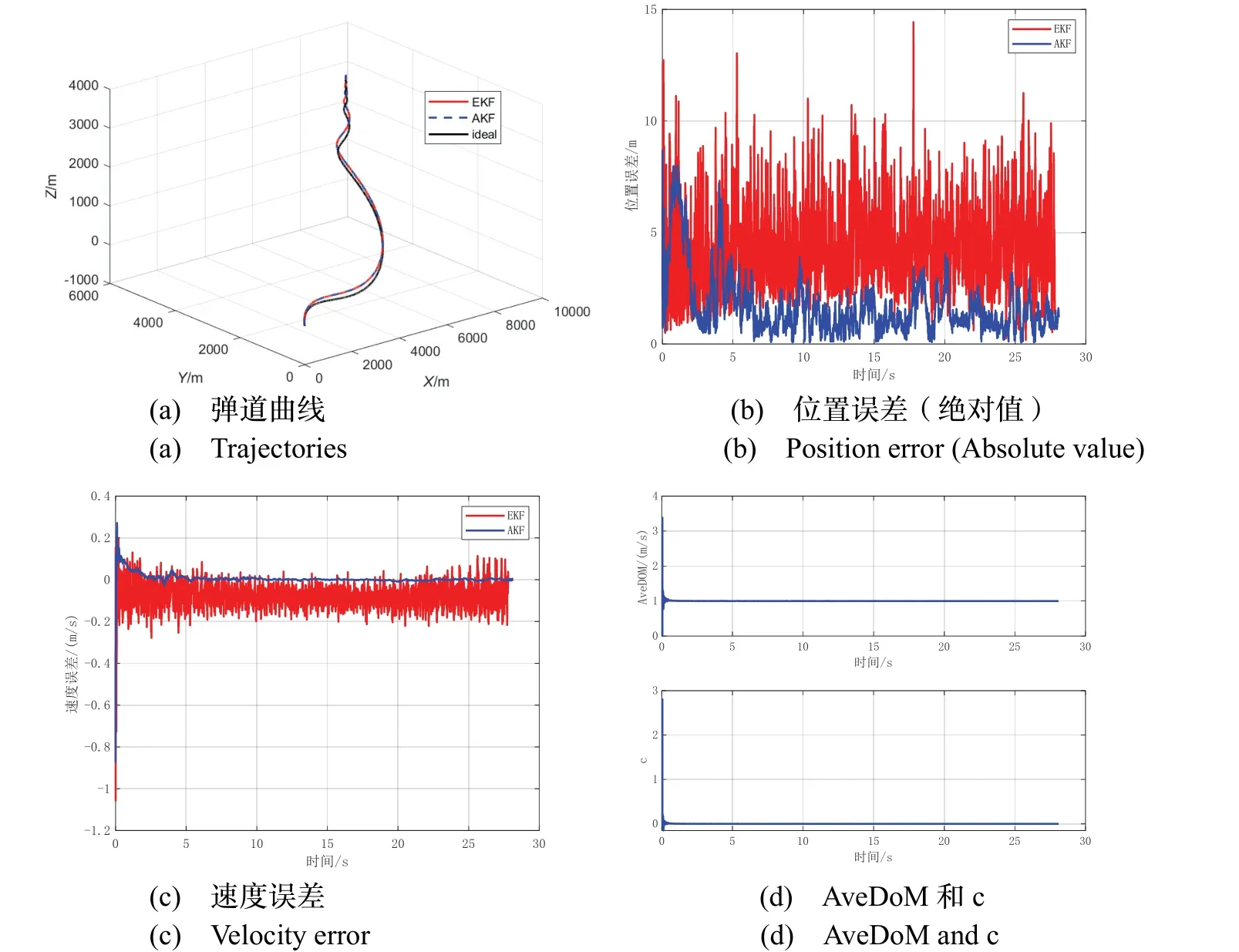
图5 无GPS 信号丢失下的仿真结果Fig.5 Simulation results without GPS signal loss

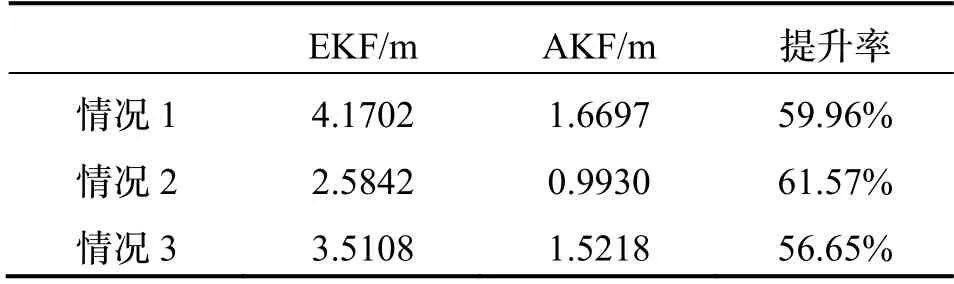
表2 平均位置误差(绝对值)Tab.2 Positioning error (Absolute value) on average

根据仿真结果，可得如下推论：

1)从弹道而言，采用所述虚拟运动状态条件约束的AKF 可实现精确制导。常速条件下，无论经典EKF还是所述AKF，其仿真弹道与理论弹道贴合度较高。变速条件下，与经典组合导航方法相比，基于所述AKF 的导航与制导方法的仿真弹药更贴近于理论弹道，脱靶量更小。

2)从滤波效果而言，当给定量测噪声方差初值与实际量测噪声有较大差距时，与经典EKF 相比，所述AKF 能快速逼近真实值，量测误差更小。通过对比各图(b)(c)的位置误差与速度误差，可发现经典EKF 的性能对初始量测噪声方差估计值精确度要求高，而所述AKF 无需精确估计。

3)从新息协方差不匹配度而言，文献[7]所述模糊算法难以控制AveDoMk稳定至1，各图(d)说明本文所述方法实现了AveDoMk的稳定控制。

4)从定位精度而言，基于AKF 的组合导航方法在三种情况下的定位效果均显著优于基于EKF 的组合导航方法，且平均定位精度提升55%以上。

图6 存在GPS 信号丢失下的仿真结果Fig.6 Simulation results with GPS signal loss

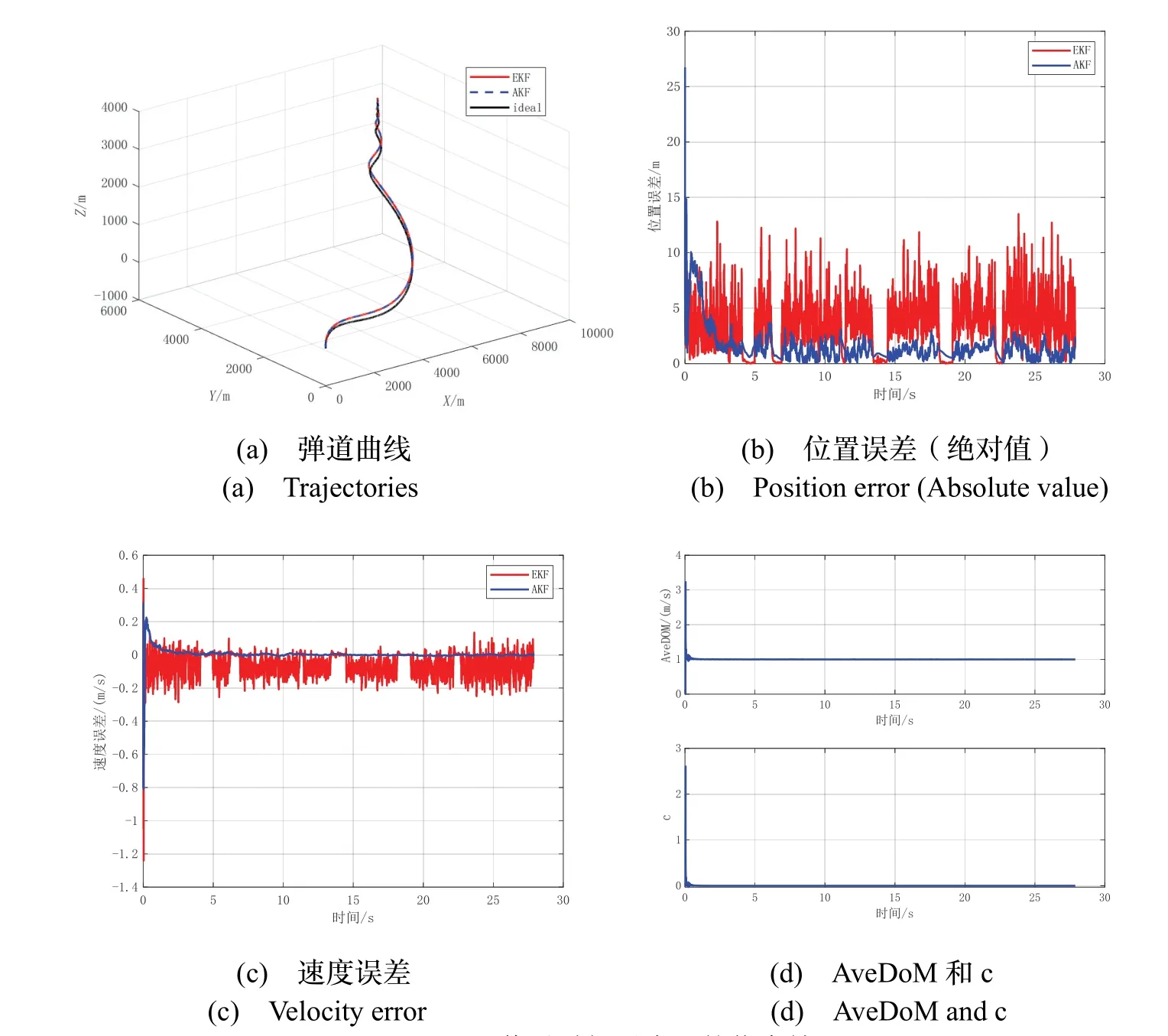
图7 GPS 信号随机丢失下的仿真结果Fig.7 Simulation results with GPS signal randomly loss

值得注意的是，在上述方法中，载体虚拟运动信息的预测精度直接决定了导航精度。对于无人机载空地制导弹药、制导炮弹、制导火箭弹等低成本、短飞时的制导弹药，虚拟运动信息预测精度较高，上述方法可作为卫星信号丢失时的一种补偿手段，亦可应用于低成本短程惯性制导弹药。

5 结论

针对SINS/GPS 松组合导航低成本制导弹药在卫星信号丢失条件下的精确导航问题，设计了基于载体虚拟运动状态预测的卫导信号补偿导航方法与基于新息协方差不匹配度的新型AKF，并通过基于实测数据的仿真实验与不同卫星信号接收环境下的数学仿真实验，验证了所提方法的有效性。所提方法优势主要体现在两个方面：

1)本方法充分利用组合导航制导弹药装备的低成本SINS/GPS 组件，在卫导信号丢失时，基于制导算法预测载体虚拟运动状态信息，对SINS 系统的惯性误差进行补偿，进而获得较为精确地导航信息。

2)当量测噪声方差无法准确预估时，基于新息协方差不匹配度的新型AKF 仍可快速估测载体的运动状态。相较与经典EKF，基于 AKF 的组合导航方法可将平均定位精度提升55%以上。

所提方法主要适用于卫导信号短时缺失的情况下，针对卫导信号长时缺失的情况，对大跨域载体运动状态的长时高精度预测，亦是后续重要研究方向。