基于电压约束的微机械谐振器幅-频耦合抑制方法
2023-03-06郭月圆
刘 恒,郭月圆,张 玉
(南京信息工程大学 电子与信息工程学院,南京 210044)
硅微机械谐振式传感器具有体积小,功耗小,可批量生产,输出为频率信号从而抗干扰性强等优势,广泛应用于加速度、压力、质量等的测量[1,2]。目前主要有两个问题制约着性能的提升:一是硅材料的杨氏模量受温度变化会导致输出频率的漂移和分辨率降低[3]。目前解决方案有三种:第一种是更换硅基材料,采用对温度敏感性小的半导体材料,如石英等;第二种是将传感器放在恒温环境工作,减少温度变化对输出频率影响;第三种是利用先进智能算法对输出频率进行温差补偿。二是微结构振动的幅度和频率耦合问题[4]。当微机械振动梁谐振幅度小于临界振幅时,忽略高阶非线性刚度项的影响,微结构等效为一个二阶弹簧-质量-阻尼系统,振动幅度与输出频率耦合可忽略不计,幅度-频率曲线不发生跳变;当振幅度超过临界振幅时,振动幅度与输出频率耦合较大,幅度-频率曲线存在不对称性和分岔,系统变得不稳定。研究者已经关注到微机械谐振传感器超过临界振幅的非线性行为,利用杜芬(Duffing)振子来建立数值模型进行分析[5],但对稳定性无控制,工程应用中受到一定限制。
传感器封装后长期工作会带来品质因数和材料特性等的变化,为了提升传感器的稳定性和分辨率,闭环测控电路需维持振梁工作在谐振状态,同时为了抑制幅度和频率的耦合,提升谐振器的稳定性,需维持振梁的恒定幅度振动[6]。自动增益控制技术被广泛应用于恒定幅度控制,而锁相环和自激振荡技术常被用来实现频率跟踪控制[7]。幅度自动增益控制包括交流自动增益控制(AC-AGC)和直流增益控制(DC-AGC)两种,其中交流自动增益采用专用的芯片,线性范围较小,调整步进大,精度较小,目前多采用直流自动增益控制方法。在直流自动增益控制中,当谐振频率锁定后,直流参考电压决定了微机械谐振传感器的振动幅度。当振动幅度过大,微机械谐振式传感器就会出现幅-频曲线的分岔,系统稳定性恶化[8]。为了满足幅度和相位要求,测控电路需要自动增益的幅度控制环路与谐振频率跟踪环路。由于两个环路的高阶和非线性问题,难以获得直流参考电压与振动幅度的关系。
针对上述问题,本文提出了一种闭环自激控制的直流参考电压约束方法,通过计算临界振幅,得到临界直流参考电压,约束直流参考电压小于临界值,抑制振动频率与振动幅度耦合,提升微机械谐振器的稳定性。
1 微机械谐振器原理及临界振幅求解
如图1所示,硅材料的音叉谐振器的结构层包括驱动部分、检测部分和谐振子部分。谐振子部分有1个音叉谐振梁和附着在谐振梁上的梳齿和平板,音叉梁被支撑并悬空;驱动部分有4 个固定的驱动梳齿结构,梳齿也在支撑下悬空,驱动梳齿和附着在音叉梁上的梳齿形成梳齿电容,作为驱动换能器;检测平板与附着在音叉梁的上平板构成检测部分的平板电容。由于微结构的制造误差,检测部分采用了平板电容结构,平板电容结构能够通过改变加载在音叉梁和检测平板之间的直流电压来调节音叉梁的谐振频率,从而实现调谐谐振频率与设计频率一致。

图1 微机械谐振器结构Fig.1 Structure of MEMS resonator
微机械谐振器的动力学方程为:
式(1)中,m为音叉谐振梁及其附着的微结构的质量,k为音叉谐振梁在工作模态的刚度,c为阻尼系数,y为音叉梁沿Y 轴方向的位移,F(t) 为静电驱动力,角频率为ω。非线性刚度k表示为:为线性刚度系数,k1和k2为一次和二次谐波项,其中音叉梁固有频率,品质因数。假设方程(1)的近似解为[9]:
由于3 次及以上谐波项作用小,当系统在无阻尼状态时,忽略其作用,系统响应的幅度值有以下关系:
当振幅过大时,系统会出现幅度-频率的耦合,谐振频率ω1与振动幅度y1为[6]:
幅度-频率曲线出现分岔点对应的振幅yb为[9]:
根据理论分析,微机械谐振器的临界振幅yc应大于分岔点对应的振幅yb,见图2。
对应的临界振幅yc为:
临界振幅yc为一次和二次谐波刚度项作用的结果,还与封装的品质因数有关。对于频率差分式微机械音叉谐振器,工作模态两个音叉梁振动方向相反,一次谐波项抵消。二次谐波刚度项主导的临界振幅yc2为:
由式(6)可知,临界振幅与品质因数Q和二阶刚度系数k2有关。对于此条件下,微机械音叉谐振器处在线性谐振阶段,储存的能量最大值Emax为:
在微结构制造后,刚度系数k0和k2为确定值,根据式(7)可知,增大品质因数Q,存储的能量减少,微机械谐振器更容易受到非线性效应影响而不稳定。
对于图1所示的微谐振器结构细化后如图3所示,音叉谐振器的刚度k0和等效质量m表示为:
式(9)中,附加平板的面内有效面积Aact为:
式(8)-(10)中,E=160Gpa,为常温下多晶硅的杨氏模量;ρ=2330Kg/m3,为常温下多晶硅的密度;Aact为附加结构的表面积;n1为梳齿电容的个数;n2是平行板电容的对数,n3是平行板电容的个数,h为微结构的厚度。L,L1,L2,L3,L4,L5为对应微结构的长度,W,W1,W2,W3,W4,W5为对应微结构的宽度,尺寸标注如图3所示。对于k2的求解,谐振梁为双端固支梁时,文献[10]给出的对应关系是:

图3 微机械谐振器结构及尺寸Fig.3 Structure and size of micromechanical resonator
常数α的取值为0.75[10]。根据式(11),k2与谐振梁的宽度W的平方成反比,W越大,对应非线性项越小。微机械谐振器的结构层采用单晶硅材料,在硅材料里掺杂高浓度的硼离子来改变微结构的导电性,衬底材料为pyrex7740 玻璃,微结构与玻璃衬底通过阳极键合。
制造的微结构划片后进行了计算机视觉辅助尺寸测量,在实物照片上标记二维尺寸,如图4所示。
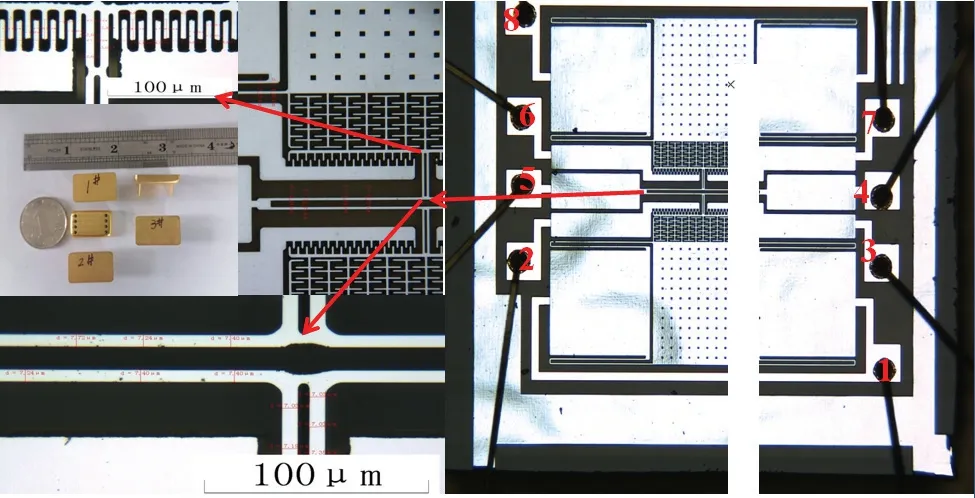
图4 微结构制造及尺寸测量和封装Fig.4 Microstructure dimension measurement and packaging
开环扫频电路如图5所示,包括电荷放大器、隔离直流后的交流放大电路、高通滤波、反相器、模拟开关、低通滤波器1、方波发生器电路[11]。
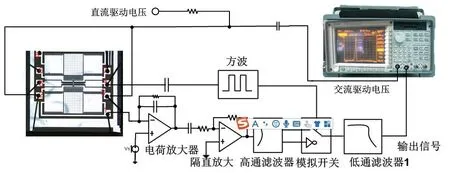
图5 开环扫频测试电路原理图Fig.5 Schematic diagram of open-loop frequency sweep test
直流稳压电源给测试电路提供直流驱动电压Vd,交流驱动电压由动态信号分析仪Agilent35670A 的1通道提供,检测端Vs由正5 V 电源分压产生,静态测试时接地,由LTC1799 电路产生858.650 kHz 的高频方波Vm。低通滤波后的输出信号接入Agilent35670A的2 通道。在交流电压的幅值为1 V,扫描范围为34-40 kHz,图6(a)为直流电压为3 V 时的幅度-频率曲线,曲线没有出现局部跳跃,谐振频率为35.754 kHz,正弦波幅值为252 mV,品质因数为1476,而继续增大直流电压到5 V 时,曲线出现局部跳跃,出现明显非线性现象,谐振频率增大为36.362 kHz,振动幅度增大为274 mV,见图6(b)(图6 中横坐标为频率,纵坐标为线性幅度比(LinMag),刻度为:30 e-3/div)。

图6 测试得到的幅度-频率曲线Fig.6 Amplitude-frequency curve obtained from test
设计的谐振梁宽度为8 μm,测试为7.24 μm,见图7,测量的品质因数为1476,α选取为0.75,结合式(6),计算得到临界振幅yc2为0.62 μm。检测平板间距设计为3 μm,测试为3.06 μm,如图8所示,临界振幅不到检测平板间距的1/3,谐振微结构达到临界振幅时不会发生吸合失效。

图7 测试的音叉谐振梁宽度Fig.7 Width of tuning fork resonance beam

图8 测试的平板电容极板间距Fig.8 Test plate capacitance plate spacing
2 基于边带比的振动幅度估算方法
2.1 估算原理
微机械谐振式传感器为了减小功耗及保护微结构不被测量环境中的固体颗粒或液体所损坏,管壳多为金属或陶瓷,封装的盖帽采用不透明的玻璃、金属、陶瓷等材料,难以利用计算机视觉方法获取真空封装后的微结构振幅,只能通过电学方法估算振动幅度。结合开环测试电路,振幅估算测试电路原理见图9。
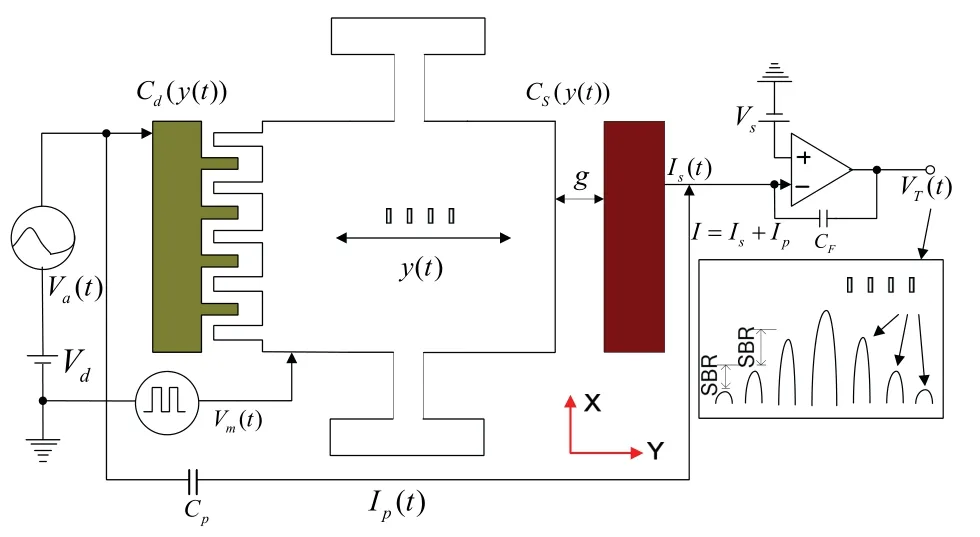
图9 基于边带比测量振动幅度电路原理图Fig.9 Circuit schematic diagram of vibration amplitude measurement based on sideband ratio
微结构振动幅度的表征是通过检测电容来反推的,在接口电路上,通过电荷放大器将变化的检测电容转换为电压VT(t),见图9。右边检测平板流过的电流I包括两部分,一部分来自流经检测电容CS的电流IS(t),另一部分来自耦合电容CP的电流IP(t)。由于电流IP(t)的变化频率与驱动电压频率ω一致,而检测电流IS(t)中也存在振动引起的频率为ω的电流,很难根据电荷放大器输出的电压VT(t)来判断结构是否处在谐振状态,测试中存在同频干扰问题[11]。所以在音叉梁上加载高频方波电压Vm(t),其幅值为Vm,角频率为ωm,。当电荷放大器的反馈电容为CF,输出电压VT(t)为:
式(12)中,Va(t)=Vasin(ω t+φ),输出电压VT(t)从频域分析,包括直流电压分量(Vd-Vs)·CP/CF,Vs,-Vs·Cs0及与驱动频率ω一致的交流电压分量Vasin(ω t+φ)·CP/CF和-Vs·βa(t)sin(ωt)/CF,高频调制后的交流分量Vm(t)·βa(t)sin(ωt)/CF。在静电驱动力作用下,音叉梁做正弦周期性运动,谐振结构的位移y(t)表示为:y(t)=Ysin(ωt),Y为振动幅度。对应的检测电容Cs(y(t))为:
式(13)中,g为检测平板初始间距,ε为封装气体的介电常数,A检测平板的正对面积,CSn为归一化检测电容。令η=Y/g为归一化振动幅度比例系数。检测电容CS(y(t))表示为:
式(14)中:
将式(14)代入到式(12)中,输出电压VT(t)中的多边带中与ωm相近的频带对应的电压幅度为:
式(16)表明,多边带中频率为ωm±j·ω处对应电压幅度近似成比例于。那么相邻两个单边带电压比也简称为SBR。归一化后的邻近边带比r(η)可以表示为:
式(17)表明,相邻单边带电压比r(η)与振动幅度比η有关,与调制电压Vm(t)和反馈电容CF无关。根据r(η)来求解η,对应的关系式为:
根据式(18)知,只要测得相邻单边带电压比r(η)就可确定振动幅度比η,而η=Y/g,在测得质量块附着的平板与谐振梁平板之间的初始垂直距离g和测得相邻单边带电压比r(η)后就可以计算得到谐振梁振动的幅度Y。
2.2 基于边带比的振动幅度测量实验
实验中的直流驱动电压Vd由直流稳压电源提供,交流电压Va(t)由信号发生器提供,检测电压Vs由稳压电路分压得到,V s为0 V 时,Vd为3 V,Va幅值为1 V,频谱分析仪Agilent 4395A 探头接在电荷放大器的输出端,阻抗为50 Ω。
图10 为驱动频率ω为20 kHz 对应的受迫振动的频谱图,+ω、+2ω、+3ω为调制频率ωm右边的边带频谱,对应频率为:ωm+ω、ωm+2ω、ωm+3ω,-ω、-2ω、- 3ω为左边的边带频谱,对应频率为:ωm-ω、ωm-2ω、ωm-3ω。边带频谱频率依次相差20kHz。左右两边对称的边带频谱由于随机噪声的影响,幅度并不完全相等。对测试的数据进行分析,以+ω和 +2ω对应电压计算后得到的η为0.0399,以-ω和 -2ω对应电压计算后得到的η为0.0412。分析图10,频谱图中还存在ωm+ω0和ωm-ω0的电压信号,对应的频率为822.898 kHz 和894.430 kHz,也说明存在一个频率为35.750 kHz 的信号被调制了,对应为白噪声激励下的音叉梁谐振输出信号。调整频率范围,观察到图11中低频段频谱不仅存在20 kHz 的驱动电压信号,还存在35.750 kHz 的谐振信号,佐证了白噪声的激励作用。
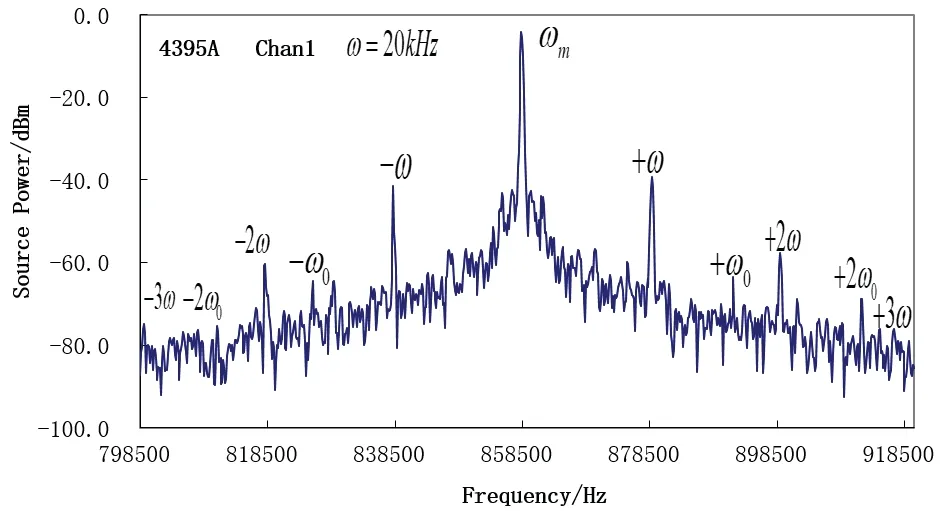
图10 电荷放大器输出信号中频段频谱(ω=20 kHz)Fig.10 Mid-band spectrum of charge amplifier output signal(ω=20 kHz)

图11 电荷放大器输出信号的低频段频谱(ω=20 kHz)Fig.11 Low-band spectrum of charge amplifier output signal(ω=20 kHz)
图12 是交流驱动电压频率为35.750 kHz 对应的频谱,在784100-932900 Hz 范围内,只有谐振信号被调制后的频谱,与图6 对应的频率扫描结果一致。基于单边带比的微结构振动幅度的电学测量不仅可以测量驱动电压下的振动幅度,还可以确定微结构的谐振频率。调节信号发生器的频率,当调制的单边带电压幅度最大时,对应的信号发生器的频率即为微结构的谐振频率,图12 为与图6(a)相同驱动电压的频谱图,在谐振状态时,对应的输出信号的电压幅度明显比图10 中ω+ 和ω- 的大。图13 与图6(b)相同驱动电压的频谱图,谐振点电压幅度明显比图12 的对应点值大。
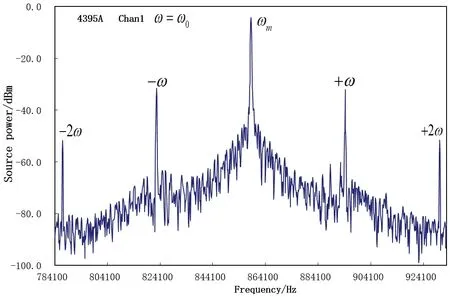
图12 电荷放大器输出信号的中频段频谱(ω =35.750 kHz)Fig.12 Mid-band spectrum of charge amplifier output signal(ω=35.750 kHz)

图13 电荷放大器输出信号的中频段频(ω =36.362 kHz)Fig.13 Intermediate band frequency of charge amplifier output signal(ω =36.362 kHz)
计算得到图13 条件下的η均值为0.04 受迫振动幅度Y约为0.122 μm;在驱动频率为35.750 kHz,对应谐振状态的η均值为0.10,振幅0.304 μm,未超过临界振幅;在驱动频率为36.362 kHz,对应谐振状态的η均值为0.28,振动幅度约为0.851 μm,超过临界值,这与开环扫频实验的幅度-频率曲线存在跳变一致。
3 闭环自激驱动原理及实验
闭环测控电路中,在高频方波调制和模拟开关解调后再经过低通滤波器1 得到正弦波信号,正弦波信号一路通过全通移相器后再经过一个固定电容与驱动梳齿电极相连,另一路通过全波整流后再通过低通滤波器2 得到幅度对应的直流电压,此直流电压与直流参考电压进行减法运算,再经过比例-积分器调节,最后通过电阻与驱动梳齿电极相连,两个环路构成直流自动增益控制(DC-AGC)。开环测试得到的正弦信号,正比于微结构的振动位移,结合图4,测控电路框图如图14。图14 中,kc为电荷放大器的增益系数,τ为低通滤波器2 的时间常数,A为滤波后得到的直流电压,VR为直流参考电压,Vd为直流驱动电压,Va为交流驱动电压,μ为移相器时间常数,kp和kI分别为比例、积分系数,kv为电压-力转换系数,与驱动梳齿有关,R(t)为热噪声产生的等效驱动力。假设谐振梁的振动位移为y(t),y(t)=a(t)cos(ω t+ϕ(t)),幅度为a(t),相位为ϕ(t),角频率为ω。
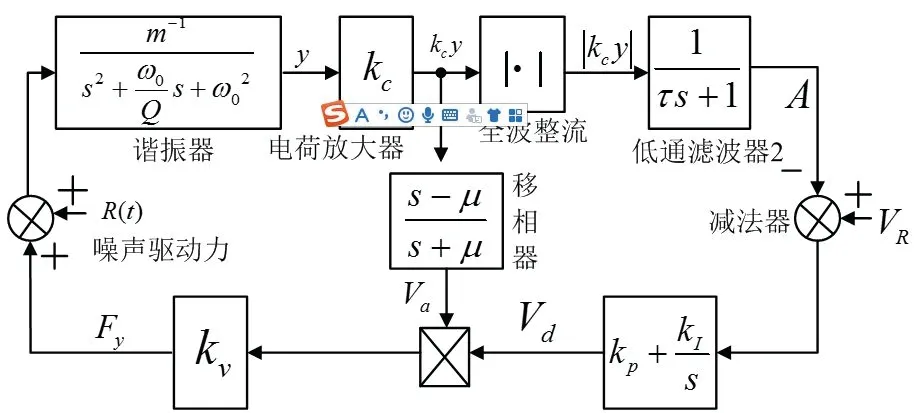
图14 微机械谐振器测控电路框图Fig.14 Measurement and control circuit diagram
根据各模块的动力学原理,建立分析模型,有[12]:
式(19)中,K=kc·kv,真空封装品质因数较大,慢时变系统状态变量变化接近为0,令各状态变量对时间求导后为0,得到振动后的稳定平衡点为:
系统起振要求直流参考电压满足:
根据式(21),V R大于静态平衡点对应的直流驱动电压,微结构才能起振。移相误差φ在理想条件下应为0,当存在相位偏移时,偏差角度越大,则需更大的VR才可起振。V R的增大,必将带来振动幅度的增大,系统稳定的条件时要求稳态的振动幅度小于临界振幅yc2,有:
式(22)中,kc由扫频实验和幅度计算确定,激励频率为35.750 kHz,谐振幅度为0.304 μm,放大后的幅度值为 252 mV,代入计算得到VR临界值为0.866 V。
通过以上分析,可以得到直流参考电压选取原则,首先,直流参考电压应大于起振电压,满足式(21);其次,直流参考电压应尽可能大,直流参考电压越大,振梁振动幅度和检测端的信噪比越大,便于振动信息提取;最后,为避免振梁非线性特性产生,直流参考电压应小于临界参考电压,满足式(22)。
闭环实验见图15,测试电路板平放在恒温实验箱中(温度误差±0.01℃)。直流参考电压调整到0.4 V,振荡波形如图16,系统上电自激经过约5 ms 稳定,波形在长时间内幅度恒定,稳态波形幅值为248 mV;增大直流参考电压到1.0 V,振荡波形如图17,自激波形较快于图16 进入幅度稳定状态,稳态波形在大时间尺度看幅度波动不大,幅值约为1.09 V,但当示波器时间刻度变小,振动幅度存在变化且周期并不完全一致。

图15 微机械谐振器测控实验设备Fig.15 Experimental equipment of micromechanical resonator

图16 微机械谐振器稳态输出波形Fig.16 Steady state output waveform of micromechanical resonator

图17 微机械谐振器大耦合下的输出波形Fig.17 Output waveform of micromechanical resonator under large coupling
利用12 位半数字频率计(Agilent53132A)和6位半数字万用表(RIGOL DM3068)对实验箱(HZ-XY-DT(H)30F-2)里的谐振器的频率和幅度进行同步采样,采样间隔均为1 s,单次采样时长均为1000 s。
图18 为幅度采集数据,直流参考电压小于临界值,振动幅度稳定,变化小于1 mV;直流参考电压大于临界值,振动幅度变化较大,在闭环自动增益电路作用下幅度变化渐近减小。利用全交叠Allan 方差分析幅度的稳定性[13,14],采样数据平均分为2 组,组长为500,步长为1,直流参考电压小于临界值,幅度偏差随时间加长稳定度提升,长时间后器件内部温度恒定,幅度扰动小;直流参考电压大于临界值,初始样本幅度波动小,但长时间后幅度均值变化大,幅度稳定度远小于前面的稳定状态,分析结果如图19所示。
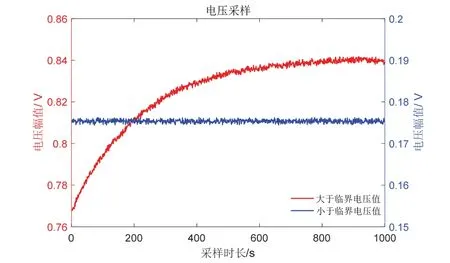
图18 幅度采集数据Fig.18 Amplitude acquisition data

图19 幅度稳定度分析Fig.19 Amplitude stability analysis
图20 为频率采集数据,直流参考电压小于临界值,谐振频率较稳定,波动幅度不超过0.1 Hz。直流参考电压大于临界值,振动幅度变化较大,波动幅度超过180 Hz,由于谐振器品质因数大,在自激振荡电路控制作用下频率变化量渐近减小。同样,利用全交叠Allan 方差分析频率的稳定性,分组跟幅度分析一致,直流参考电压小于临界值,频率偏差随时间加长稳定度变差,但总体趋近于0.01 Hz,测控电路能维持1000 s 内的0.01 Hz 的频率偏差;直流参考电压大于临界值,初始频率波动幅度大,但在自激振荡电路作用下,频率变化范围减小,1000 s 内频率偏差大于0.1 Hz,频率稳定度远小于稳定状态,结果见图21。

图20 频率采集数据Fig.20 Frequency acquisition data
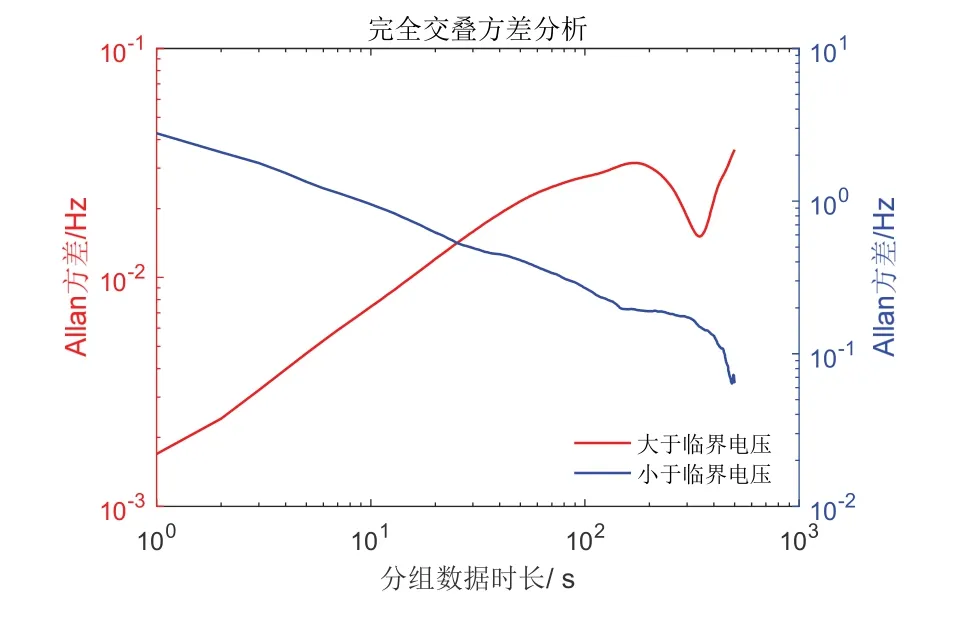
图21 频率稳定度分析Fig.21 Frequency stability analysis
4 结论
本文介绍了一种抑制微机械谐振器的幅度-频率耦合方法并进行了验证,方法的核心是通过调节自激振荡控制电路的直流参考电压来控制振梁振动幅度小于临界振幅。首先,通过理论分析确定了音叉梁谐振器的临界振幅与振梁的宽度、检测平板间距和品质因数有关,针对制造的静电驱动电容检测型音叉谐振器,采用了计算机辅助视觉测量方法获得了微结构的尺寸,包括谐振梁的宽度和检测平板间距;利用开环扫频方法获得了品质因数,计算得到临界振幅为0.62 μm。其次,介绍了一种频谱边带比的振动幅度测试方法,实验测试稳态振幅为0.30μm,非稳态为0.85μm,与理论分析一致。最后,构建了自激振荡闭环测控电路分析模型,并利用平均周期法获得了振幅与直流参考电压的线性关系,临界直流参考电压应小于0.866 V。恒温实验测试表明:直流参考电压为0.4 V,谐振器恒定幅度振动;直流参考电压为1.0 V,谐振器振动幅度不恒定,谐振器稳定性变差,通过调节直流参考电压能有效抑制幅度-频率的耦合。
