一种考虑加表不对称误差的冗余惯组标定方法
2023-03-06于玲燕
罗 睿,李 鹏,于玲燕
(1.北京航天控制仪器研究所,北京 100039;2.北京航天时代激光导航技术有限责任公司,北京 100094)
惯性导航系统可以自主提供姿态、速度和位置信息,而惯性测量组件(以下简称惯组)是惯性导航系统的核心组成部分[1,2]。目前,惯性导航系统在航天、航空和军事领域广泛应用。惯性导航系统的精度直接关系到航天器和武器装备的使用效能,惯组标定精度的高低对导航精度有直接影响。惯组误差包括确定性误差和随机误差两部分,其中确定性误差是捷联惯导系统最主要的误差源。因此,在惯组使用前必须通过标定试验确定惯组的各项误差参数,并进行补偿[3]。
在日益复杂的使用环境下,要求惯导系统在达到一定精度的同时,还要具备高可靠性[4]。器件级冗余技术是目前常用的提高系统可靠性的方法。未使用冗余技术的惯组在有一个惯性器件损坏时,整机功能就会失效[5,6],而使用了器件级冗余的惯组通常包含3 个以上的陀螺和加表,当遇到同样的情况时,惯导系统仍可正常工作[7]。但这也给标定带来了新的问题。
文献[8]中提到的标定方法仅适用于正交配置的3陀螺、3 加表捷联惯组。文献[9-11]中采用安装误差来描述敏感轴,且安装误差阵对角线元素为1,难以较好地描述斜置敏感轴的空间位置。而文献[12]中提出的冗余惯组标定方法未考虑加表不对称误差的影响,会降低惯性导航系统动态导航性能。
本文对冗余结构激光惯组建立了数学模型,考虑加表不对称误差影响,采用12 位置法和速率法,通过迭代求解提高加速度计的正负刻度因数及零偏的标定精度,得到陀螺和加速度计的零偏、安装误差、刻度因数等参数,提高了惯性导航系统动态导航性能。
1 冗余激光捷联惯组标定模型
冗余激光捷联惯组通常采用如图1-2所示的方式配置。如图1所示的12 表冗余惯组包含6 个陀螺仪和6 只加表,6 个敏感轴依次排列在以x 轴为对称轴的圆锥的母线上,且间隔的角度相等,是一种圆锥形配置的冗余捷联惯组。在任意2 个敏感轴失效的情况下仍能算得X、Y、Z 轴上的角速度和加速度,并进行导航解算。
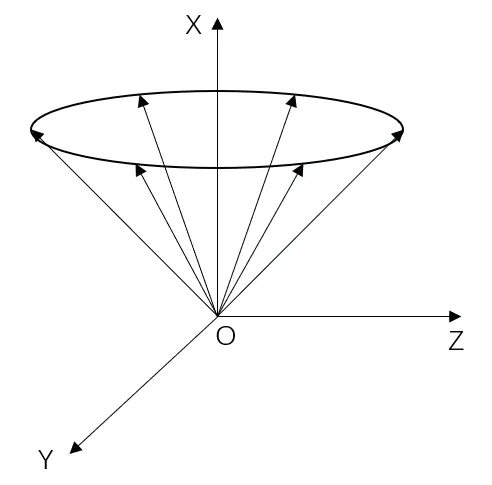
图1 圆锥形配置的12 表冗余惯组Fig.1 12-sensor redundant IMU in a conical configuration
如图2所示的10 表冗余惯组包含5 个陀螺仪和5只加表是一种“正交+斜置”方式配置的冗余捷联惯组,S 轴与X、Y、Z 三个敏感轴均成54.74°夹角,T 轴与S 轴关于平面YOZ 对称。在任意1 个敏感轴失效的情况下仍能算得X、Y、Z 轴上的角速度和加速度,并进行导航解算。
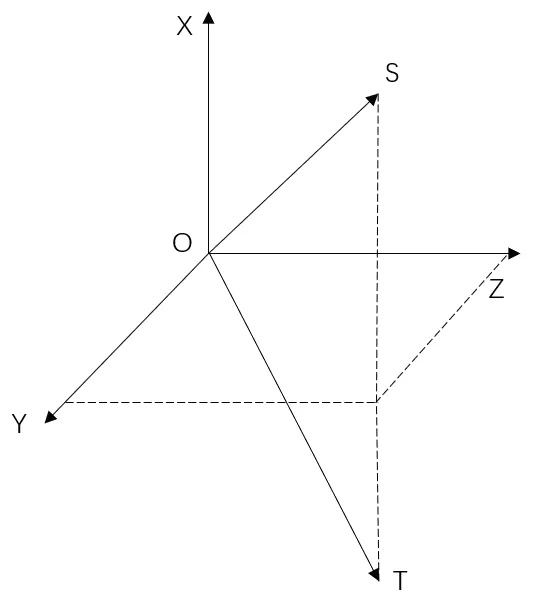
图2 “正交+斜置”方式配置的10 表冗余惯组Fig.2 10-sensor redundant IMU in a ‘orthogonal+incline’configuration
工程上一般使用一阶线性方程来描述激光陀螺仪和石英挠性加速度计的误差模型。圆锥配置使得所有器件的敏感轴均不与坐标轴重合,故需使用各惯性器件的敏感轴在载体坐标系b 系中的方向余弦来描述各惯性器件安装关系。
由于激光陀螺对载体运动的加速度不敏感,可在陀螺的输入输出模型中忽略加速度项。则可将其描述为
其中,G为陀螺脉冲输出,为陀螺刻度因数,为陀螺安装关系矩阵,为输入参考角速度,ε为陀螺零偏。
与陀螺相似,忽略加速度计二次项系数,加速度计输入输出模型可表示为
其中,A+为加表正脉冲输出,A-为加表负脉冲输出,为加表正刻度因数,为加表负刻度因数,为加表安装关系矩阵,为正输入参考比力,为负输入参考比力,∇为加表零偏。
2 标定路径编排
合理的标定路径编排可有效激励各项误差参数[13]。位置实验采用12 位置法,在不具备北向基准的实验室仍可使用,只是位置间的转动须为90°的整数倍,这样各位置的输入角速率可互相抵消。假设转台已调平,初始位置与北向夹角为一未知角度α(规定北偏西时,α>0),表1 是本文采用的一组12 位置,其中的东、西、南、北均为近似指向。其中输入比力(fx,fy,fz)的单位为重力加速度g,输入角速率(ωx,ωy,ωz)的单位为rad/s,为简化表示,将地球自转的北向分量ωiecosL记为ΩN,将其天向分量ωiesinL记为ΩU。

表1 12 位置编排Tab.1 12 position orchestration
速率实验采用三轴正反转速率实验,在相同时间内分别绕载体系的X、Y、Z 轴正反转3 圈,正反转时间t 相同,其中的东、西、南、北均为近似指向,具体编排如下:
初始位置为上东北,绕X 轴正反各旋转3 圈;
初始位置为南上西,绕Y 轴正反各旋转3 圈;
初始位置为北西上,绕Z 轴正反各旋转3 圈。
3 标定参数计算
3.1 加表参数计算
设每个位置停留时间为t,第j个位置第i个加表的脉冲输出总和为Aji,fu为沿天向的比力输入,单位为g,Eaxi、Eayi和Eazi为i 轴方向余弦。考虑到不同配置方式下加表可能是正刻度因数也可能是负刻度因数,表 1所示各位置加表脉冲数为:A1i=(K1Eaxi fu+K1∇i)t,A2i=(K1Eaxifu+K1∇i)t,A3i= (-K2Eaxifu+K2∇i)t,A4i= (-K2Eaxi fu+K2∇i)t,A5i=(K3Eayi fu+K3∇i)t,A6i=(K3Eayi fu+K3∇i)t,A7i= (-K4Eayifu+K4∇i)t,A8i= (-K4Eayi fu+K4∇i)t,A9i=(K5Eazi fu+K5∇i)t,A10i=(K5Eazifu+K5∇i)t,A11i= (-K6Eazifu+K6∇i)t,A12i= (-K6Eazifu+K6∇i)t。
其中K1与K2不同时为正或负刻度因数,即K1=Kai+时,K2=Kai-;K1=Kai-时,K2=Kai+。K3与K4以及K5与K6有类似的互斥关系,且K1与K2、K3与K4以及K5与K6三组之间互不影响正或负刻度因数的取值。
将上述12 式两两相加可得:
将式(3)减去式(4)、式(5)减去式(6)、式(7)减去式(8)整理可得:
3.1.1 常用标定方法及其缺陷
常用标定方法先假设式(9)-(11)中的(K1-K2)∇i、(K3-K4)∇i和(K5-K6)∇i三项可以忽略,由此先求出平均刻度因数,这三项下文简称为加表不对称误差。
并由此求出安装关系:
最后求出该轴加表的零偏:
根据已求得的安装关系和零偏通过以下方法计算该轴的正负刻度因数。
假设i 轴加表的方向余弦为(Eaxi,Eayi,Eazi),且Eaxi,Eayi,Eazi中绝对值最大的为Eayi,则:
若Eayi> 0,
若Eayi< 0,
常用方法的缺陷在于:
1.计算平均刻度因数时忽略了加表不对称误差,并将由此产生的误差传递至根据平均刻度因数计算出的安装关系,导致标定结果的加表不对称度小于实际不对称度;
2.计算加表零偏时没有考虑加表刻度因数的不对称性造成的影响;
3.计算正负刻度因数时,使用的安装关系和零偏含有误差。
另外,当加速度计不对称度较大时,式(9)-(11)中的(K1-K2)∇i、(K3-K4)∇i和(K5-K6)∇i三项已无法忽略,上述方法中的引入的误差会进一步放大。如图3所示,根据仿真结果,随着加表的不对称度增大,该轴的零偏标定误差迅速增大。
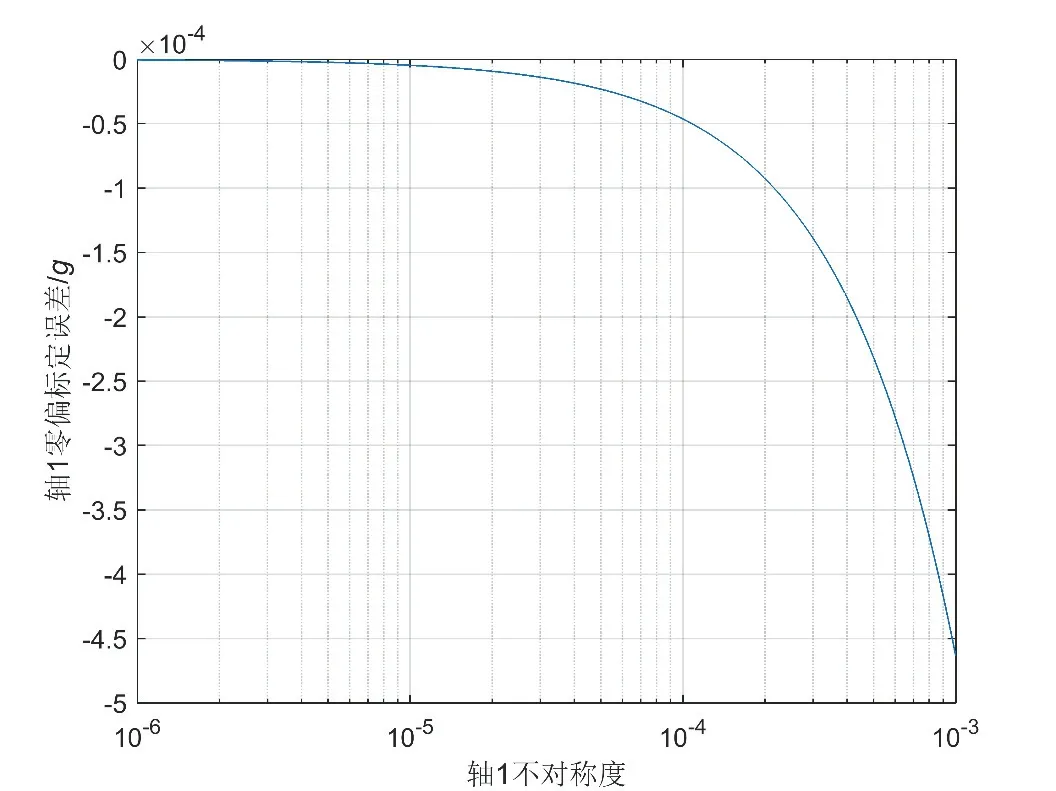
图3 加表不对称度对零偏标定误差的影响Fig.3 The effect of accelerometer asymmetry on its zero-bias calibration accuracy
i 轴加表的不对称度ξi(无量纲)定义如下:
3.1.2 考虑加表不对称误差的迭代式标定方法
为消除加表不对称误差对标定造成的影响,本文提出了一种迭代方法,在保留三项不对称误差的前提下,迭代估计所有的标定参数。
具体计算方法如下:
在初次计算时令∇i=0(i=1 ~6),则式(9)-(11)中的(K1-K2)∇i、(K3-K4)∇i和(K5-K6)∇i三项在初次迭代时为零,可得:
其中,
则可得Eaxi、Eayi和Eazi:
根据Eaxi、Eayi和Eazi的符号可确定K1、K2、K3、K4、K5和K6是正刻度因数还是负刻度因数。
使用最小二乘法即可求得Kai+、Kai-和∇i,然后根据求得的∇i和正负刻度因数重新计算Eaxi、Eayi和Eazi并重新计算其他参数,如此迭代反复估计所有参数,即可得到最优估计,具体迭代过程如图4所示。
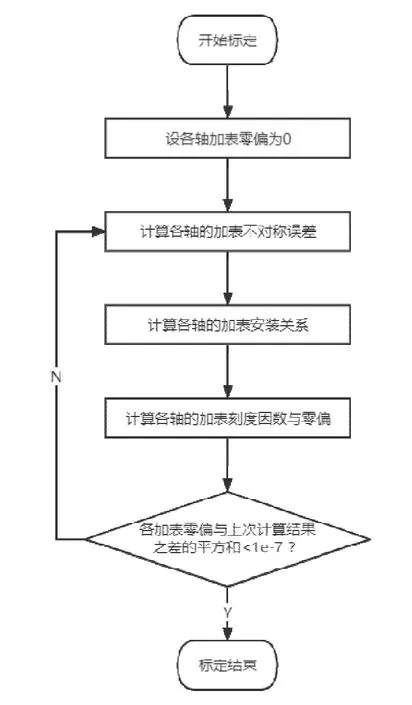
图4 迭代过程Fig.4 Iterative process
3.2 陀螺参数计算
根据速率实验编排,绕X 轴正反转N圈(N=3),正反转时间t相同,记Gxi+为绕X 轴正转第i个陀螺的脉冲输出总和,Gxi-为绕X 轴反转第i个陀螺的脉冲输出总和,Kgi(pulse/")为i 轴陀螺刻度因数,εi(°/h)为i 轴陀螺零偏,Egxi为i 轴陀螺在b 系X 轴上的方向余弦。则有:
式(20)中两式相减,整理后可得:
其中,i=1,2…6。
同理,分别绕Y、Z 轴正反转N圈,正反转时间均为t,则有:
由式(21)(22),可推得第i个陀螺的刻度因数和安装关系:
通过位置实验可计算出陀螺的零偏。设每个位置停留时间为t,在第j(j=1,2…12)个位置的第i(i= 1,2…6)个陀螺的脉冲输出为Gji,则第i个陀螺的零偏εi可表示为:
4 算法验证
某10 表“正交+斜置”方式配置的冗余捷联惯组采用了5 个光纤陀螺和5 个石英挠性加速度计的冗余设计。陀螺的零偏稳定性优于0.05(°/h),加表的零偏稳定性优于2 ×10-5g。对该10 表惯组分别使用本文所述迭代标定算法与常用标定算法进行标定,表2 为10 表惯组两种标定方法的加表标定结果对比。

表2 10 表惯组加表标定结果对比Tab.2 Comparison of accelerometer calibration results of 10-sensor IMU
对于加表刻度因数,10 表惯组的两种标定方法结果之差为1(pulse/g)量级。对于加表零偏,10 表惯组的两种标定方法结果之差为1 ×10-4(g)量级。
表3 为两种方法标定所得的加表不对称度对比,从表中可以看出,采用迭代方法标定所得的加表不对称度的绝对值均大于常用方法,恰好验证了3.1.1 节中所述的常用方法缺陷的第1 点,由于忽略加表不对称误差相当于默认加表对称性良好,因此常用方法计算得出的加表不对称度也要小于真值,而迭代标定方法则不存在这个问题。
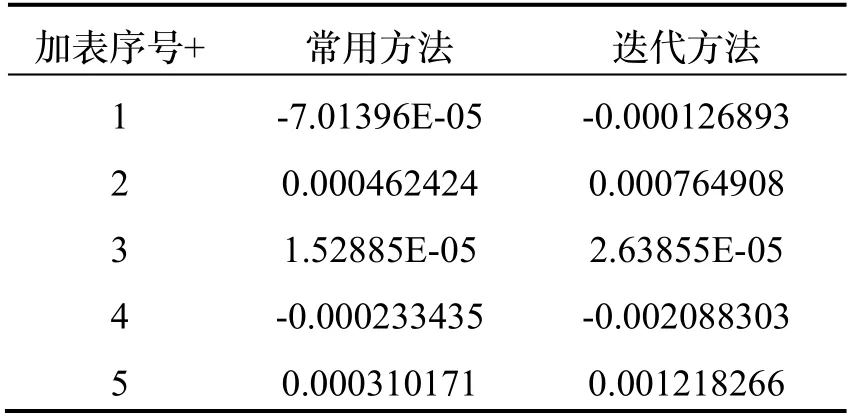
表3 10 表惯组加表不对称度对比Tab.3 Comparison of accelerometer asymmetry of 10-sensor IMU
图5、图6 分别为10 表惯组迭代标定过程中正负刻度因数和零偏的收敛曲线,从图中可以看出,在迭代5~7 次后每个轴的加表刻度因数和零偏基本收敛。
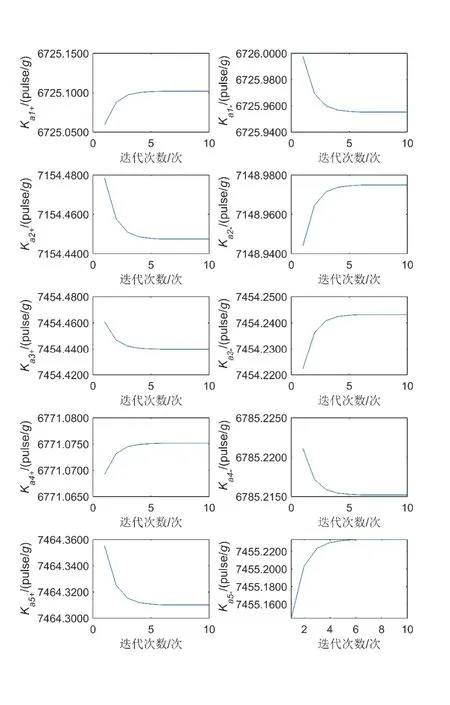
图5 10 表惯组刻度因数迭代曲线Fig.5 Scale factor iteration curves of 10-sensor IMU
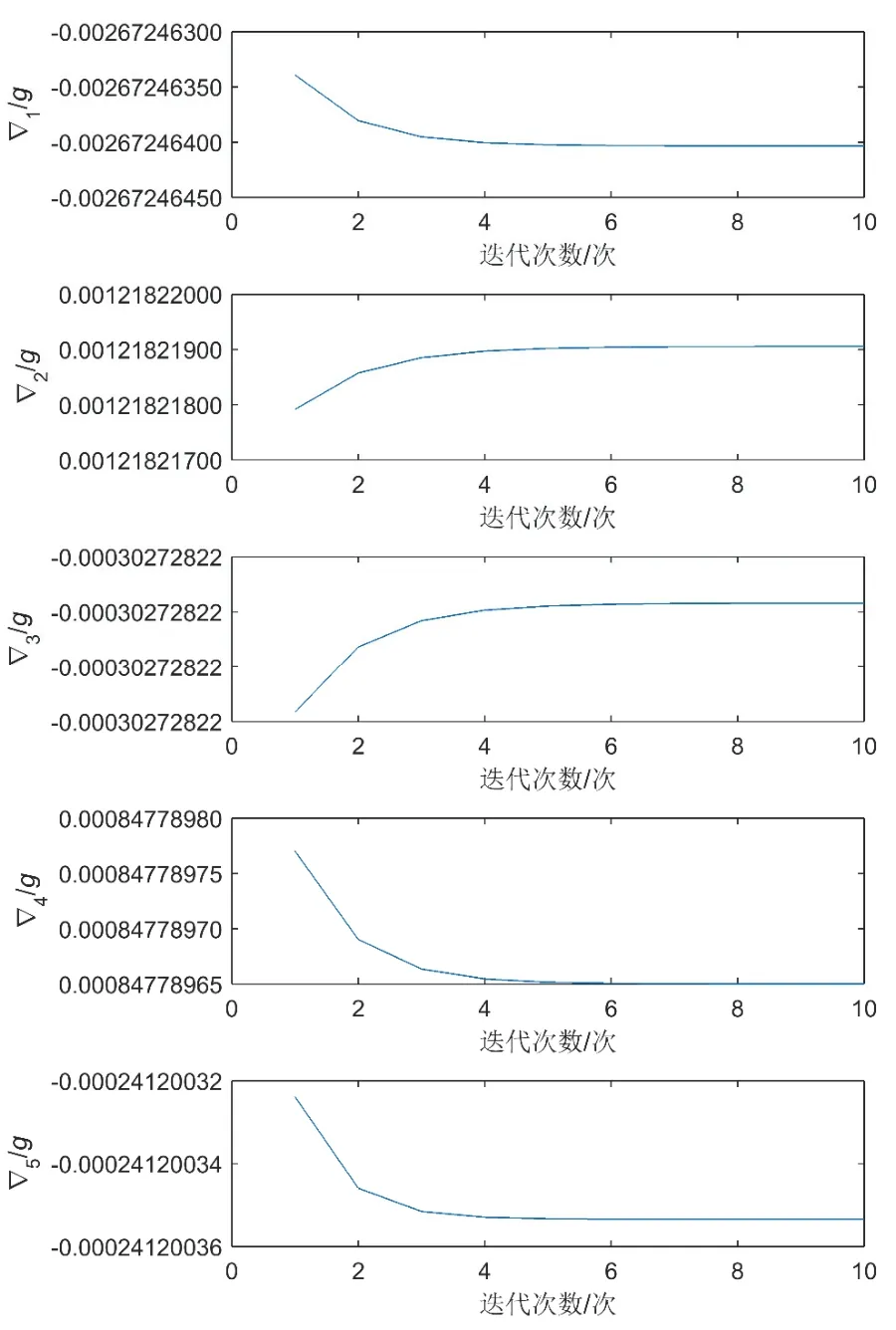
图6 10 表惯组零偏迭代曲线Fig.6 Zero-bias iteration curves of 10-sensor IMU
分别使用两种方法标定所得的参数进行5100 s 动态导航实验,在动态导航实验中通过转台对惯组的翻转,更好地激励加表不对称误差。图7-9 为10 表惯组动态导航的姿态曲线、速度曲线以及位置误差对比图。

图7 某10 表惯组动态导航姿态曲线Fig.7 Dynamic navigation attitude curves of 10-sensor IMU
图8是10表惯组两种标定方法的动态导航速度对比图。可以看出在约一个舒拉周期的导航时间内,使用迭代方法标定的导航速度曲线在大多数时间里绝对值小于常用方法。这意味着在动态导航过程中,迭代方法在大多数时间里有更小的速度误差。
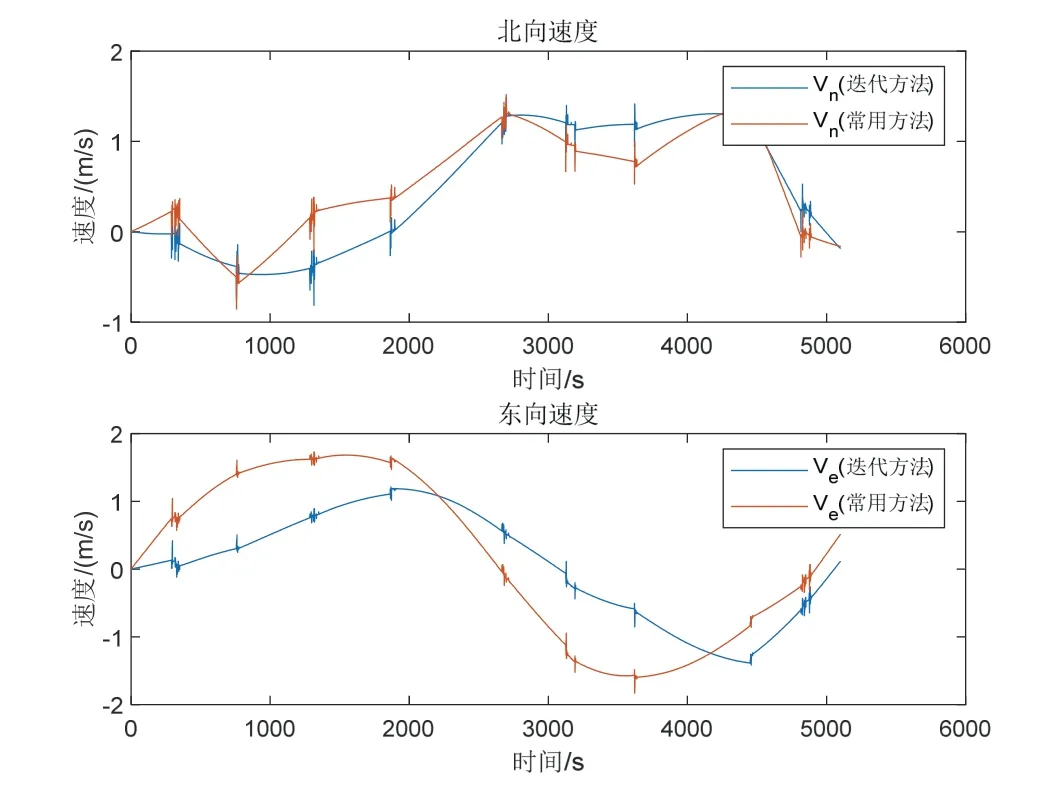
图8 某10 表惯组动态导航速度曲线Fig.8 Dynamic navigation speed curves of 10-sensor IMU
由图9 可见迭代标定方法在整个动态导航过程中位置误差均低于常用标定方法,并且10 表惯组5100 s动态导航末端位置误差降低了约400 m,验证了本文所述标定方法的有效性。

图9 某10 表惯组动态导航位置误差对比Fig.9 Dynamic navigation position error of 10-sensor IMU
5 结论
本文分析了冗余捷联惯组的输入输出模型,提出了在加表刻度因数不对称度较大时使用迭代求解来提高标定精度的方法,给出了详细的求解标定参数的数学推导过程,建立了冗余捷联惯组的标定算法。试验结果表明:本文提出的迭代求解的标定方法可有效消除加表不对称误差及其对其他参数标定的影响,是一种简洁可靠的冗余捷联惯组标定方法,使冗余惯性导航系统的动态导航位置精度提高了约13.3%,对冗余导航系统动态导航应用具有一定的参考价值。
