面向工业能耗分析的大数据技术及其应用

甘玉涛

（河北司法警官职业学院， 河北 石家庄 050081）

0 引言

机器学习算法是大数据技术的重要部分，在工业领域被广泛应用。大数据技术发展，要求对工业能耗数据分析，便于制定相应的节能策略。由此提出了基于大数据技术的线性回归算法与支持向量机分类算法，分别对能耗数据中的线性和非线性数据进行预处理。线性回归主要用来解决回归问题，即预测连续值的问题[1]。支持向量机按监督学习（Supervised learning）方式对数据进行二元分类的广义线性分类器[2]。对处理非线性问题，能够处理高维数据，具有较强的泛化能力，并且适用于小样本数据。结合K-Means算法对能耗的海量数据进行聚类分析、预测，该算法能根据较少的已知聚类样本的类别确定部分样本的分类，对能耗数据的聚类和分析能够增加精确度和速度，由此能够获得对工业能耗具有影响的相关因素。对海量数据进行预处理，聚类分析，关联分析和预测，进而便于节能降耗措施和能耗优化建议的提出，对于工业的能耗分析和节能策略制定具有重要意义。

1 基于大数据技术的机器学习算法研究与能耗分析应用

1.1 结合线性回归与支持向量机分类算法研究

在大数据条件下，机器学习算法在互联网技术发展的重点，也是支持工业能耗分析的首选。此次研究结合线性回归算法与支持向量机算法，分别对能耗数据的线性问题和非线性问题进行处理，算法具有较好的泛化能力、鲁棒性和可解释性，便于之后的算法分析。线性回归算法是回归算法中的重要算法和模型，比非线性回归算法更容易拟合未知参数，在实际生活中运用广泛。以数据集｛yi，（xi1，xi2，…，xip）｝为例，自变量和线性回归模型中因变量以直接和可预测的方式联系在一起，并建立相应的模型说明这两个变量之间的关系，相关表达见式（1）：

式中：s1为误差变量；x，y 都为向量；xiTθ 为向量的内积；xiT为向量的转置；p 为自变量个数。线性回归主要应用在预测和辨别冗余的方向，对工业能耗数据进行处理和分析，便于之后的算法进行进一步分析。

分类是将不同类别的样本根据某一个标准进行区分和对新样本进行类别预测，对工业能耗数据进行分类，是对其进一步分析的首要操作。由Vladimir N.Vapnik 提出的支持向量机（Support Vector Machine，SVM）算法是用于分类的非概率学习算法[3]。对于支持向量机分类算法来说，能够根据训练样本的SVM模型对样本点的空间进行表示和描述，以两个类别为例，在通过决策平面之后，分成两个不同的区域，也就是类。为了获得经过决策函数的新数据的准确分类结果，可以将其添加到适当的区域。所以说，SVM 算法对非线性数据的分类过程，是将数据进行线性分类后，将数据原始的空间维度转换为高维特征的空间。以一组训练样本为例，SVM将其定义表达见式（2）：

式中：yi为样本xi的类别，值为1 或者-1，xi为一个维度为p 的向量。SVM由此构造一组超平面，将和以最大间隔分离的超平面，表示见式（3）：

式中：b/‖w‖为超平面法向量方向的截距；w 为法向量；b/‖w‖能够将两个线性平面转为超平面，如式（4）所示：

在式（4）中2/‖w‖为两个平面之间的间隔，两个平面可以准确地分离信息。SVM 的一个特点是随着泛化能力的提高对区间的需求增加，因此需要将目标定义为二次优化形式，见式（5）：

并且将式（5）采用拉格朗日算法的乘子算法得出目标函数见式（6）：

由此获得最优化式，见式（7）：

间隔越大造成的误差就越小，所以选择分类平面的标准是使任意训练样本距离平面的距离尽量大。

1.2 基于K-means 聚类算法的能耗数据聚类分析算法实现

数据的预处理包括数据的清洗和标准化，聚类分析即数据的离散化，将数据按照特定顺序和特定格式进行分类。在大数据环境下，聚类算法中的K-Means算法是数据挖掘的流行算法，该算法是将多个数据划分为一定数量的聚类中，并且每一个数据点都会有与其距离对应的均值代表的聚类[4]。此次研究通过该算法能耗数据进行聚类分析，能够对数据进行分析，为了识别某些样本的分组，通过使用减少数量的已识别聚类样本的分类来移除树的部分。该算法具有通过迭代过程优化和校正修剪的功能。为了确定某些样本的聚类，算法通过迭代返回到先前已识别的聚类，优化了在支持向量机分类算法的初始监督学习样本分类不合理的地方[5]。分析小样本的特点可以降低聚类时间的总体复杂性。

K-Means 算法能够将数据划分类不同的集合，在算法中，设置n 个数据点，每个数据采用d 维的向量表示，该算法目的为减少组内的差异，即群内离差达到最小。相关计算见式（8）：

式中：S 为划分的集合S=｛S1，…Sk｝；μi表示中的所有点的中心点；xj为数据点；k 为划分的集合数量。迭代最优是K-Means 算法的常用算法，设置K 个初始均值点，算法通过交替地遵循两个阶段来重复该过程，即分配阶段和更新阶段步骤。将各数据点分配到个聚类中，使类分离差最小[6]。按照离差为平方欧氏距离计算出点附近的最近均值，见式（9）：Si（t）={xp：‖xp-μi（t）‖2≤‖xp-μj（t）‖2∀j，1≤j≤k.（9）

通过聚类中归属的数据点，能够计算出新的均值中心点，计算见式（10）：

至此当分配的步骤不变时，K-Means 算法收敛。将聚类算法应用至具体平台功能的聚类分析中，相关的运行流程见图1。

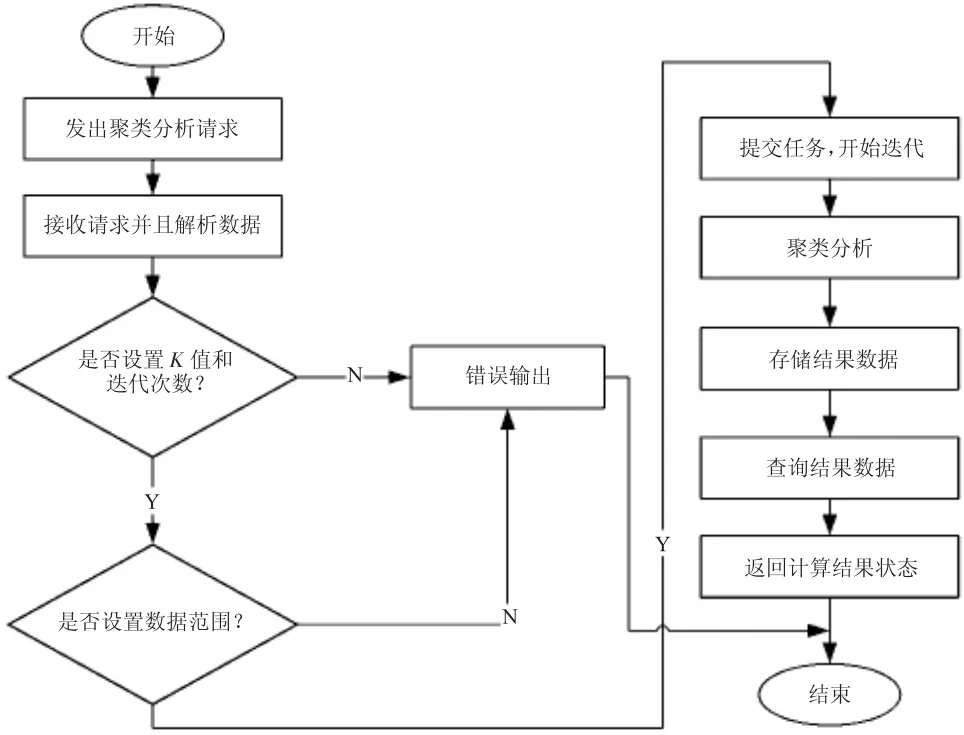
图1 聚类分析流程

图1 中，首先发出聚类的请求，解析数据后，设置K 值和迭代次数，然后设定数据的范围，提交相关的任务进行迭代筛选，然后进行聚类分析，存储相关数据后对数据查询，就可以看到最终的聚类结果。

2 工业能耗分析算法的大数据技术平台性能实验

2.1 实验准备与设计

为了对基于线性回归算法和向量机分类算法结合处理数据，与K-Means 聚类算法分析数据，并且应用至工业能耗分析平台进行性能分析，此次研究设计一项实验进行验证。实验中将工厂分为3 个区域，采用NodeAddr 区分，针对实施监控的耗能信息采用实时功率进行表示，每隔500 ms 进行数据点采集。聚类维度选用设备id、使用的起始日期、工作的时长、工人工龄、工作区域节点地址，分组对三个区域进行相关维度的实时能耗进行记录。通过不同的分群数量对聚类分析结果影响进行分析，即K 值选取3、5、7。计算、研究聚类结果，获得各维度的KL（Kullback-Leibler divergence）散度与之相匹配。其中KL 越大，表示该维度的聚类结果与分群的点相关度越高。

2.2 实验结果统计与计量分析

为了比较不同的聚类维度的KL 情况，此次实验将三个区域的实时能耗信息计算出相应的KL 值后，K 取5 和7 的KL 结果展示了部分数据，如表1。可以看出，当K=3 时，分类群B 中的工作时长KL 值最大，所以分类群B 中工作时长的相关度较高，在分类群C中，工人工龄的KL 大小在其次，工人工龄的相关度在分类群C 中的相关度较高。当K=5 时，分类群B 中的工作区域节点地址维度在各个分类群组中的KL相差很小，工作时长和工人工龄两个维度在其中KL值较大，相关度较高。当K=7 时，各个聚类维度与K=5 的大体相似，相关度也基本类似，所以K 取3～5为宜。

表1 不同维度和K 情况下的KL 散度值

基于以上，对不同的工作区域节点地址、工人工龄、设备工作时长三个关键的聚类维度进行了进一步分析，图2 为对能耗的相关分析结果。图2-1 为各工作小组的平均能耗，可以看出，第2 组与第7 组的平均能耗比其他组的平均能耗小，所以针对该两个小组，进一步进行了分析。图2-2 为该两个小组的设备工作时长与平均能耗之间关系折线图，可以看出，随着工作时长的增加，平均能耗逐渐增加，并且在35～40 min，平均能耗达到了最高。图2-3 为工人工龄与平均能耗之间关系的折线图，可见随着工人工龄的增加，平均能耗随之下降，在1～2 年时间的能耗极高，在第三年左右稳定下来，分析原因为工人的技能熟练度为其中的影响因素，可见对新员工培训极其重要。

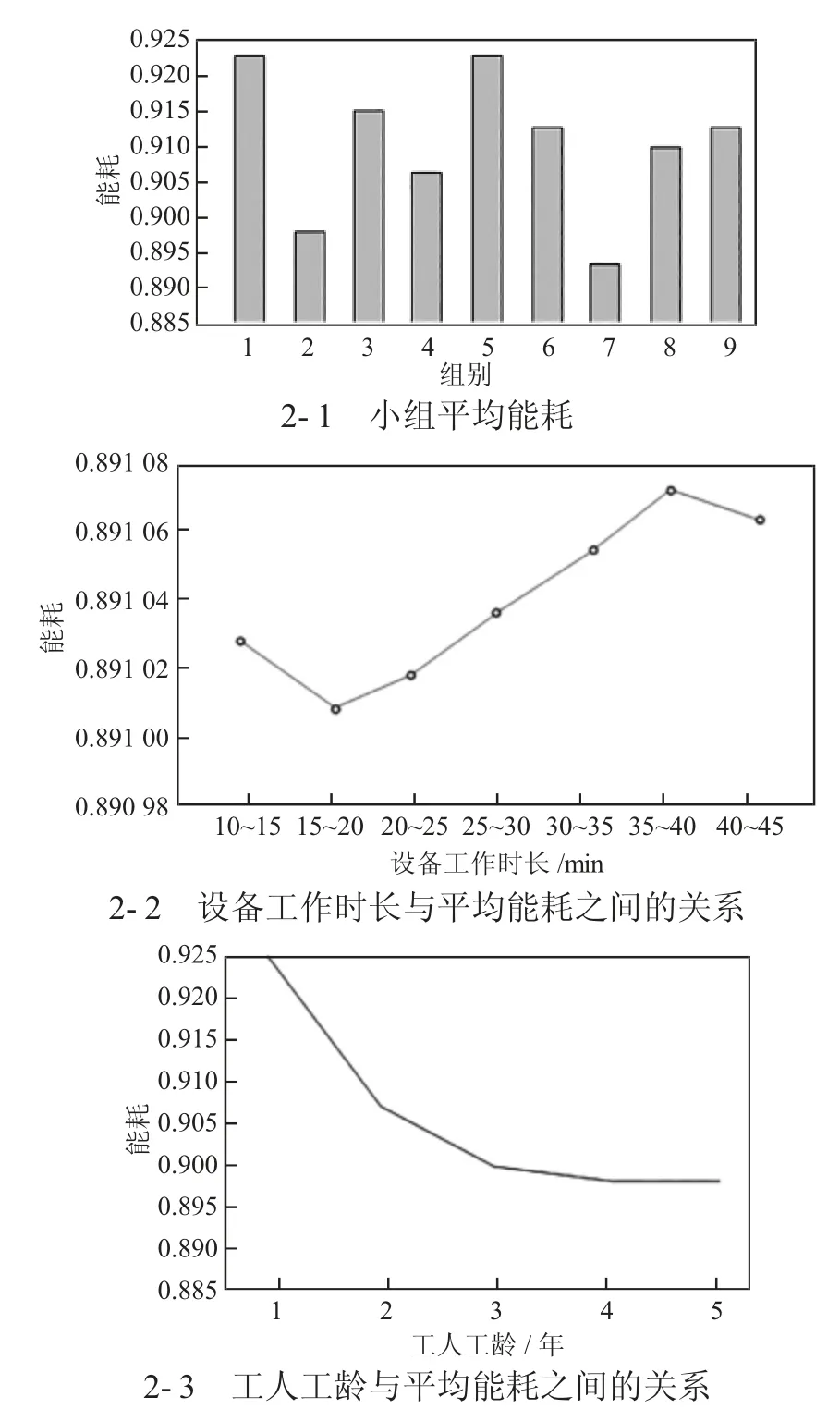
图2 平均功耗与设备工作时长、工人工龄之间的关系

3 结论

随着大数据技术的发展，对工业能耗进行分析，得出其中的影响因素，能够提前对能耗节约提出相应的节能策略。此次研究为了对工业耗能进行更加准确地分析，提出采用线性回归算法与支持向量机算法结合，对能耗数据进行预处理，然后通过K-Means 算法对能耗数据进行分析，应用至相关的能耗分析平台的核心功能算法中，特此设计一项实验验证性能和可行性。实验表明，当K=3 时，工作时长KL 值最大，相关度较高，工人工龄KL 大小在其次，相关度较高。当K=5 时，工作区域节点地址维度在各个分类群组中的KL 相差很小，工作时长和工人工龄两个维度在其中KL 值较大，相关度较高。分析工作时长和工人工龄维度对能耗的具体关系，对此提出相应的节能策略具有参考性。但是此次实验所设置的影响因素相对较少，还需要对多个维度进一步全面地考虑和分析。