预应力混凝土空心方桩堆放层数判定条件的探讨

邱振贵 冼景成

（1 广东三和管桩股份有限公司；2 福州大学 土木工程学院）

0 前言

预应力混凝土预制桩经工厂化流水机组法工艺生产制造[1]，需运至成品库贮存，最后装车运输至施工现场。产品在成品库、运输过程中以及施工现场的堆放不当都有可能造成质量问题和场地的利用不合理。国家标准GB/T 13476-2009《先张法预应力混凝土管桩》[2]对管桩的堆放层数做出了相关规定，却未明确堆放层数的计算方法和依据。何友林[3]探讨了PHC管桩堆放层数的计算方法，推导出管桩着地平放时最底层桩所受弯矩和应力的关系，计算了PHC 管桩在不同堆放层数下的最大弯矩和最大应力，从而得到不同规格的PHC 管桩堆放的最大层数。

基于上述管桩堆放的规定与研究分析知，预制桩堆放时，最底层桩受重力荷载影响所产生的内力最大，桩身容易开裂，导致产品质量的不合格。本文通过对预应力混凝土空心方桩（以下简称空心方桩）在不同堆放层数下底层桩按两支点法支承时的受力情况进行分析，计算了不同堆放层数下底层空心方桩的内力。在底层桩采用两支点法支承时，分别比较了以桩身抗裂弯矩值和以混凝土轴心抗拉强度标准值作为判定条件计算确定的可堆放最大层数，从而为空心方桩产品的堆放提供了理论依据。

1 理论分析

1.1弯矩值与应力值分析

行业标准JG/T 197-2018《预应力混凝土空心方桩》[4]对空心方桩的堆放做出了规定：空心方桩应按规格、长度分别堆放。空心方桩堆放时，长度不大于15m的，最下层宜按两支点放置在垫木上；长度大于15m 的拼接桩，最下层应采用多支点堆放，垫木应均匀放置且在同一水平面上。若堆放场地地基经过特殊处理，也可着地平放。

研究对象为单节长度、规格型号均相同的空心方桩（单节长度不大于15m）最下层按两支点支承堆放时底层空心方桩的受力情况。采用两支点支承堆放时，底层空心方桩堆放和受力状态如图1所示。

图1 两支点支承时底层空心方桩受力状态

图中：

q——荷载集度，即单节单位长度空心方桩由自重引起的荷载，kN/m；

L——单节桩长，m。

根据结构力学[5]静定结构受力分析可知，当支点位置负弯矩与跨中正弯矩在数值上相等，即MB=MC=ME时，空心方桩由重力荷载引起的弯矩内力最小，按此支点位置支承的空心方桩更不易开裂，进而保证产品的质量。两支点支承时底层空心方桩所受弯矩如图2所示。

图2 两支点支承时空心方桩的受力弯矩图

此时，两支点的位置距两端的距离x为：

x= 0.21L⑴

最大弯矩Mmax应按式⑵计算：

式中：

n——堆放层数。

可知，堆放层数越多，底层空心方桩所受的荷载越大；单节桩越长，桩身承受的弯矩越大。

根据材料力学[6]弯曲应力分析可知，桩身横截面上离中性轴最远的各点处正应力最大。横截面上最大弯矩处对应的最大拉应力σmax应按式⑶计算：

式中：

Wz——换算截面抵抗矩,换算截面抵抗矩应按式⑷计算。

式中：

Iz——换算截面惯性矩；

ymax——横截面上距中性轴最远的点到中性轴的距离。

由于空心方桩是由混凝土和钢筋等材料预制而成，在计算截面惯性矩时，考虑将空心方桩配置的钢筋换算成能够承受拉应力的同种强度等级的混凝土，即按换算截面惯性矩代入计算。

考虑到空心方桩是采用先张法工艺在截面上施加预压应力，因此，计算横截面上最大弯矩处对应的实际应力值时，应减去混凝土的有效预压应力值，即横截面上最大弯矩处对应的实际应力值σ实际按式⑸计算：

式中：

σ实际——横截面处最大弯矩对应的实际应力值；

σce——混凝土有效预压应力值。混凝土有效预压应力值按JG/T 197-2018 标准中给出的计算方法进行计算，其计算结果如表1所示。

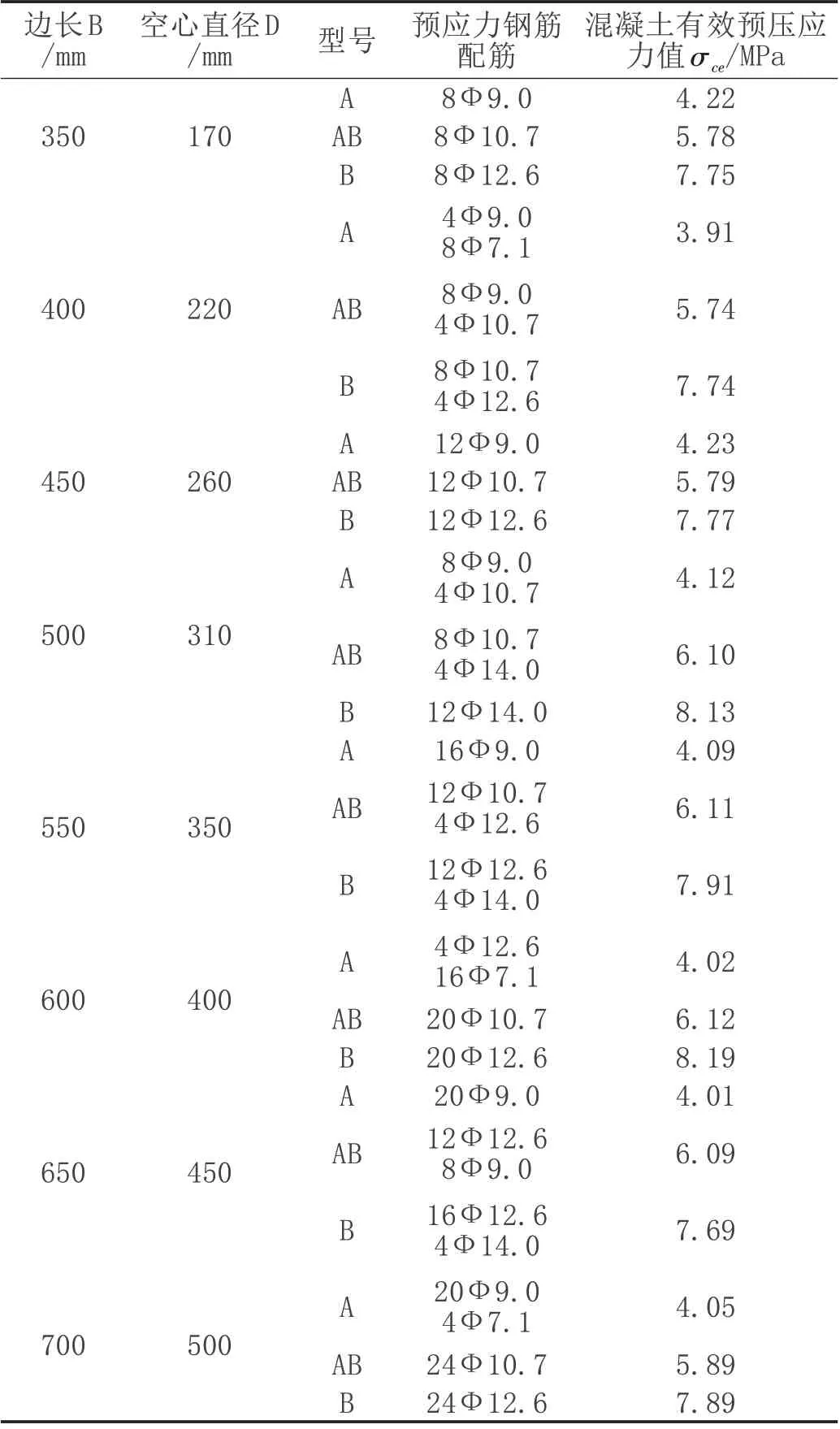
表1 各规格型号空心方桩的混凝土有效预压应力值计算结果

1.2堆放层数分析

1.2.1以抗裂弯矩值作为判定条件

当采用抗裂弯矩值作为评判依据确定底层空心方桩在两支点支承下可堆放的最大层数时，底层桩堆放时产生的最大弯矩应小于或等于桩身抗裂弯矩值，即Mmax≤Mcr。

此时，空心方桩可堆放的最大层数n 可按式⑹计算：

式中：Mcr——桩身抗裂弯矩值。

1.2.2以混凝土轴心抗拉强度标准值作为判定条件

当采用混凝土轴心抗拉强度标准值作为评判依据确定底层空心方桩在两支点支承下可堆放的最大层数时，底层桩堆放时产生的实际拉应力值应小于或等于桩身混凝土轴心抗拉强度标准值，即σ实际≤ftk。

此时，由式⑵、式⑶、式⑸联立知，空心方桩可堆放的最大层数n可按式⑺计算：

2 计算分析

采用两支点法支承堆放时，分别以抗裂弯矩值和以混凝土轴心抗拉强度标准值为判定条件进行计算得到的各规格型号空心方桩的可堆放最大层数如表2所示。

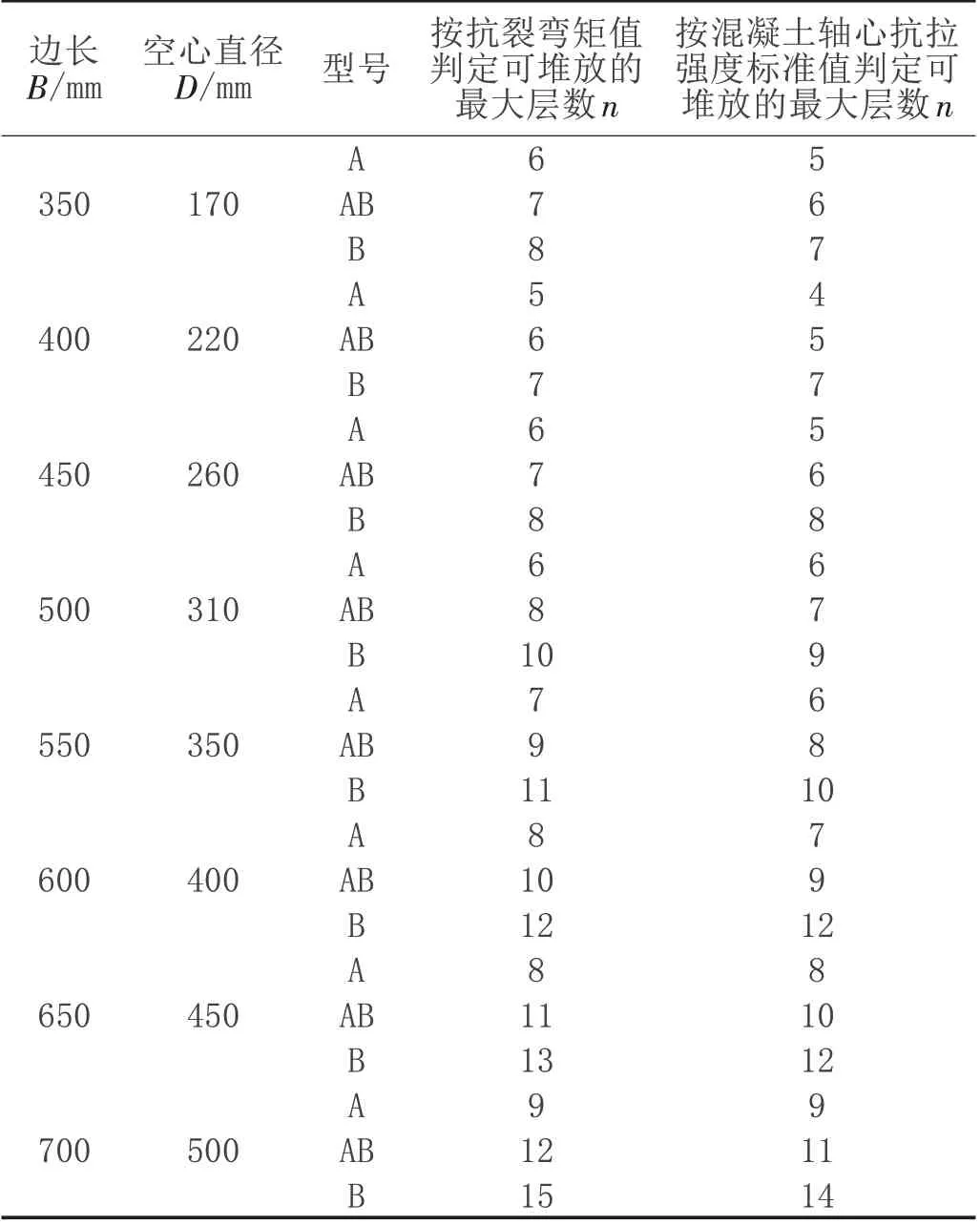
表2 各规格型号空心方桩计算的可堆放最大层数

通过以抗裂弯矩值和混凝土轴心抗拉强度标准值为判定条件计算的空心方桩可堆放最大层数对比发现，以混凝土轴心抗拉强度标准值计算得到的最大可堆放层数略微偏小，但两者数据相差不大。空心方桩可堆放的最大层数与桩身截面模量相关，随桩的规格增大而增加。

3 结论

⑴计算结果表明，两种判定条件计算得到的最大可堆放层数差别不大，可作为空心方桩堆放层数的理论依据，用于指导实际。但理论应与实际结合，堆放层数还应综合其他因素（如安全、场地情况）进行多方面的考虑。在满足安全堆放的前提下，方可参考。

⑵本文仅探讨了空心方桩底层桩按两支点支承时可堆放最大层数的判定条件。当场地经过特殊处理，且空心方桩着地平放时，若不考虑地面的变形，底层空心方桩横截面上下侧混凝土受压，内孔壁在外部荷载作用下将产生拉应力，受力较为复杂。采用此堆放方式的受力情况，还有待进一步研究。