火灾环境下特高压钢管塔的最小安全距离研究
2023-03-03李聪聪凌晨冰孟祥俊伟肖庆彪冯立言江文强
李聪聪,凌晨冰,孟祥俊伟,肖庆彪,冯立言,江文强
(华北电力大学 机械工程系,河北 保定 071003)
0 引言
利用特高压输电技术可以实现能源的远距离、大容量输送[1]。在研究输电线路安全运行的影响因素时,不仅要考虑内部因素,如螺栓连接滑移[2]等,还要考虑外部因素。输电线路所经过地区的极端气候,如低温[3]、覆冰[4]、强风[5]、火灾[6]等,都有可能对特高压输电铁塔造成破坏,影响输电线路的正常运行。
钢材是特高压输电塔的重要构成材料,其力学性能对输电塔的安全性有显著影响。当特高压输电塔遇到森林火灾时,其钢结构构件的屈服强度和弹性模量会在高温下发生改变[7];当构件温度达到1 000 ℃以上时,钢材的屈服强度只有常温下的1/4,钢结构几乎丧失承载力。因此,有必要对特高压输电铁塔在火灾条件下的安全性问题开展研究[8]。
文献[9]为了探究钢结构在真实火灾场景下的热力响应,提出了 FDS-ABAQUS火热结构耦合的分析方法。相较于传统采用ISO834标准升温曲线加载方式,模拟结构更接近真实火灾场景下的结果。但是作者在文章中选用例证模型较为简单,缺乏对复杂构件模型的验证。
文献[10]利用火灾动态模拟器(Fire dynamics simulator,FDS)分析了大跨度钢桁架拱桥在2种不同的火灾场景下的温度场分布,然后使用有限元软件 ABAQUS分析了钢桁架拱桥结构在不同火灾场景下的力学性能的变化;但是,FDS与ABAQUS耦合数据为烟气温度,故结果精度较低。
文献[11]分别利用 FDS和传热公式得到了机场航站楼屋顶钢火灾时局部构件的温升曲线;然后使用有限元软件计算了结构在设定的火灾场景下的力学性能;给出了构件的失效标准。然而,此方法也存在计算结果精度低的问题。
文献[12]开展了真实的火灾时钢构件的温升实验,构建了火灾场景下大空间建筑钢构件的理论温升模型,提出了一种烟气以及钢构件温度场的预测方法;通过实验和理论结果数据对比,结合非规律变化的烟气温度场,验证了预测方法的可行性。
文献[13]为了研究钢桁架结构在热力耦合作用下的受力性能、钢屋架的耐火能力,利用ABAQUS软件进行了分析模拟实验。结果表明:在火灾下,该钢屋架变形均在合理范围内,最大应力也满足结构安全性要求。但是,文中所采用的标准升温曲线未能准确描述构件实际温度变化情况。
为了反映真实森林火灾环境下特高压钢管塔温度场变化,本文利用FDS软件模拟不同火灾场景下铁塔主要构件的温度场;在此基础上,计算得出火灾时主材局部最大应力和屈服强度之间的关系;根据铁塔的安全性要求,给出火灾条件下特高压钢管塔的最小安全距离。
1 安全距离及判定
选取某典型特高压钢管塔主材为研究对象:主材一共分为8段,采用法兰连接;每段为10 m,直径为1.5 m;总高度为80 m。
以北方气象条件为例,取特高压钢管塔工作环境为:海拔0 m,相对湿度20%,标准大气压。
1.1 分析流程
(1)火灾时,钢管塔主材温度的获得。使用FDS对不同的火灾场景进行模拟;通过热电偶分别获取各火灾场景下钢管塔主材的最高温度。
(2)主材屈服强度折减系数的计算。根据《建筑钢结构防火技术规范》[14],依据建筑规范中屈服强度的折减公式计算各火灾场景下特高压钢管塔主材的屈服强度折减系数。
(3)钢管塔安全距离的判定。根据主材的屈服强度折减系数,判定主材是否受到火场的影响,以及是否满足强度设计标准。
1.2 判定依据
在火灾中,当钢结构达到一定温度时,其屈服强度将发生变化。根据《建筑钢结构防火技术规范》,高温下普通钢材屈服强度计算公式为
式中:fyT为温度为Ts时钢材的屈服强度,MPa;fy为常温下钢材的屈服强度,MPa;f为常温下钢材的强度设计值,MPa;Rγ为钢构件抗力分项系数,这里取1.1;Tη为高温下钢材强度折减系数。
在设定火灾场景时,本文综合考虑了空气湿度、大气压强、氧气含量等环境因素;以此为基础,探究大风工况下火源与主材距离关系。
2 火灾场景仿真建模
2.1 模型简化及火灾场景设置
在所设定的仿真火灾场景内,计算对象主要有火源、森林火场和特高压钢管塔主材,如图1所示。图1中,森林火场取4排5列有效区域。将实际树木简化为简单的几何模型后,以简化后的几何模型为基础进行网格化[15]。
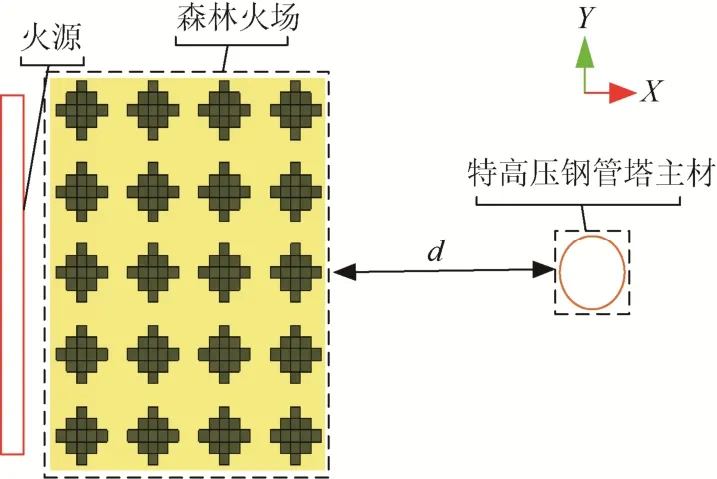
图1 森林–钢管塔主材火灾场景设置Fig. 1 Fire scene setting of forest-main material of steel pipe tower
根据森林火场到主材距离d的不同设定六种火灾场景,具体如表1所示。

表1 火灾场景设定Tab. 1 Fire scene setup
2.2 网格敏感性分析
在进行数值模拟计算时,计算区域网格的尺寸将直接影响模拟计算的精度和收敛性。考虑过小的网格也会引起较大的计算误差,因此:计算时,先使用粗糙的网格试运算;然后逐步将网格细化,直到前后2次模拟结果相近;最后,选择其中一即可。
通过上述的网格敏感性分析,得到网格尺寸经验值为火源特性直径的 1/10。特征火焰直径计算如式(4)所示。
式中:D*为网格尺寸;Q为火源热释放速率,kW;ρ∞为常温下的空气密度,kg/m3;T∞为环境绝对温度,K;Cp为空气的定压比热,J/(g·℃);g为重力加速度,m/s2。
若整个计算区域采用统一网格,则网格数量会较多,进而影响计算速度。因此本文采用分块网格:将整个区域分成森林火场区域、主材模型区域和烟气羽流区域。前2个区域采用细网格,烟气羽流区域采用粗网格。最后,将3个区域的网格按要求拼接。
2.3 探测装置布置
为采集主材结构温度以及周围烟气羽流温度变化数据,根据表1绘制火灾场景A1—A6的火灾模型,并在主材表面和周围设置热电偶 T1—T8。图2示出了火灾场景模型及探测装置分布。

图2 火灾场景及探测装置分布Fig. 2 Schematic diagram of fire scene and distribution of detection devices
2.4 边界条件及初始条件设定
常年平均风速设为5 m/s。
整个计算域共有6个面。将边界左侧面设为进风面。忽略土壤热传导,将边界下表面设为绝热壁面。边界其余的面设为通风面。
当火灾发生时,受计算域内外压差的作用,高温烟气将从通风表面溢出,新鲜空气将从通风表面补入[16]。
2.4.1 热物理性参数及燃烧化学反应式
FDS反应库中提供了多种物质燃烧反应,用户也可以根据需要自定义反应。
在本文所研究的森林火灾中,主要可燃物是木材,燃料方程式为:(C1.7O0.74N0.002)+1.021 21(O2+3.76N2)→1(0.964 384CO2+0.003 655CO+0.85H2O+0.0319 61C+3.840 76N2)。
背景气体为氧气和氮气组成的空气混合物。
燃烧时,木材与空气发生反应,生成1.5%的烟气和0.4%的CO。
特高压钢管塔材料设为Q345,密度为7 850 kg/m3,其在高温下的热物理参数如表2所示。
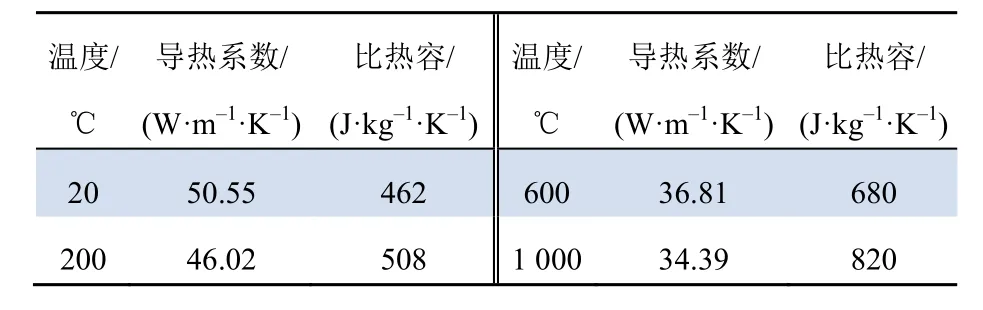
表2 特高压钢管塔材料的非线性热物理参数Tab. 2 Non-linear thermophysical parameters of UHV steel tube tower materials
2.4.2 火源的热释放率以及树木的热解参数
在实际森林火灾中,中等强度森林火灾多发且蔓延范围非常广;所以,本文选取中等强度森林火灾为模拟工况。
考虑计算条件,取小片有效森林区域作为火场区域,设置带状火源为:长15 m、宽0.5 m、热释放速率[17]为46 mW/m2。
火灾蔓延的过程主要是材料热解的过程。森林火灾的蔓延,主要是树冠燃烧蔓延。树冠和树干的热物理和热解参数[18]如表3所示。
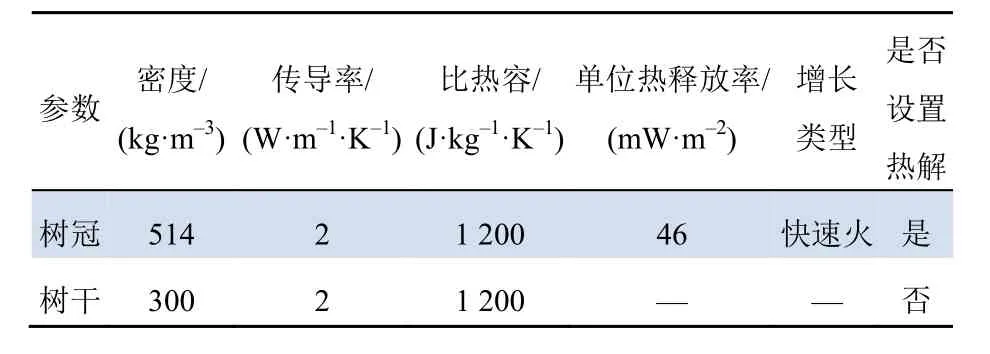
表3 树木的热物理参数和热解参数Tab. 3 Thermal physical parameters and pyrolysis parameters of trees
火源单位热释放率随时间变化曲线如图3所示。

图3 火源单位热释放率曲线Fig. 3 Heat release rate curve of fire source
3 数值分析
3.1 森林火场与主材的热作用
当森林火灾发生时,森林火场和主材之间存在热对流和热辐射2种热作用。
图4示出了500 s时森林火场温度等值面。图4中,红色等值面代表火焰层,其他均为烟气层。
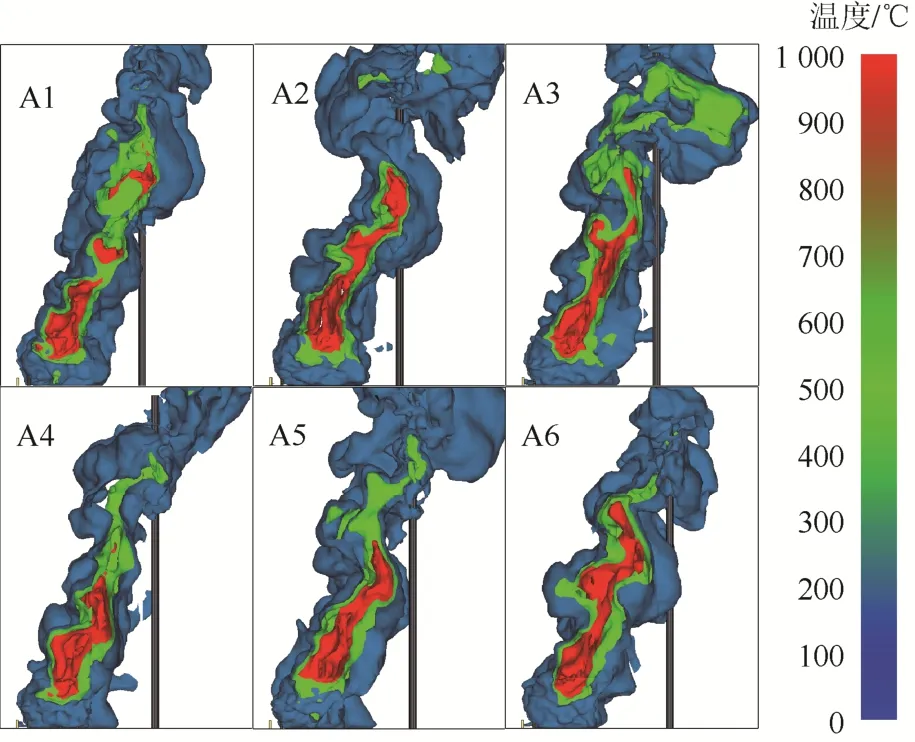
图4 森林火场温度等值面图(t=500 s)Fig. 4 Isosurface map of forest fire field temperature
图5示出了各火灾场景主材热辐射强度。
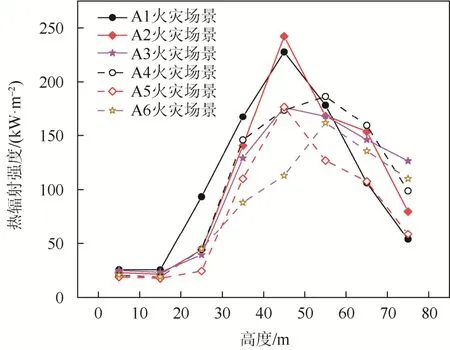
图5 主材热辐射强度Fig. 5 Thermal radiation intensity of main material
从图5中可以看出:
对于A1、A2、A3和A5火灾场景,在主材50 m高度以下的位置,热辐射强度随着高度的增加呈增大趋势;50 m以上时,热辐射强度迅速降低。
在A4和A6火灾场景中,在主材60 m高度以下位置,主材钢管热辐射强度随着高度的增加呈增大趋势;60 m以上时,热辐射强度迅速降低。
综合考虑图4、图5可以得出:主材距离火场14 m~17 m时,热辐射强度随着主材距离火场距离增加逐渐减弱;主材距离火场13 m时,主材受到热辐射强度最大,为 242 kW/m2。对于各火灾场景,在主材高度0~50 m区间段,主材受到热辐射作用逐渐上升;60 m~80 m区间,主材热辐射作用减弱。主材所受热辐射强度最强位置为50 m附近。
3.2 主材温度变化趋势
主材不仅会受到森林火场热对流和热辐射作用,主材各部分也会进行热传导。森林火场与主材之间距离的不同,主材温度分布也会随之发生改变。
火灾高峰时的主材温度分布如图6所示。各场景下钢管塔主材各测点温度分布如图7所示。
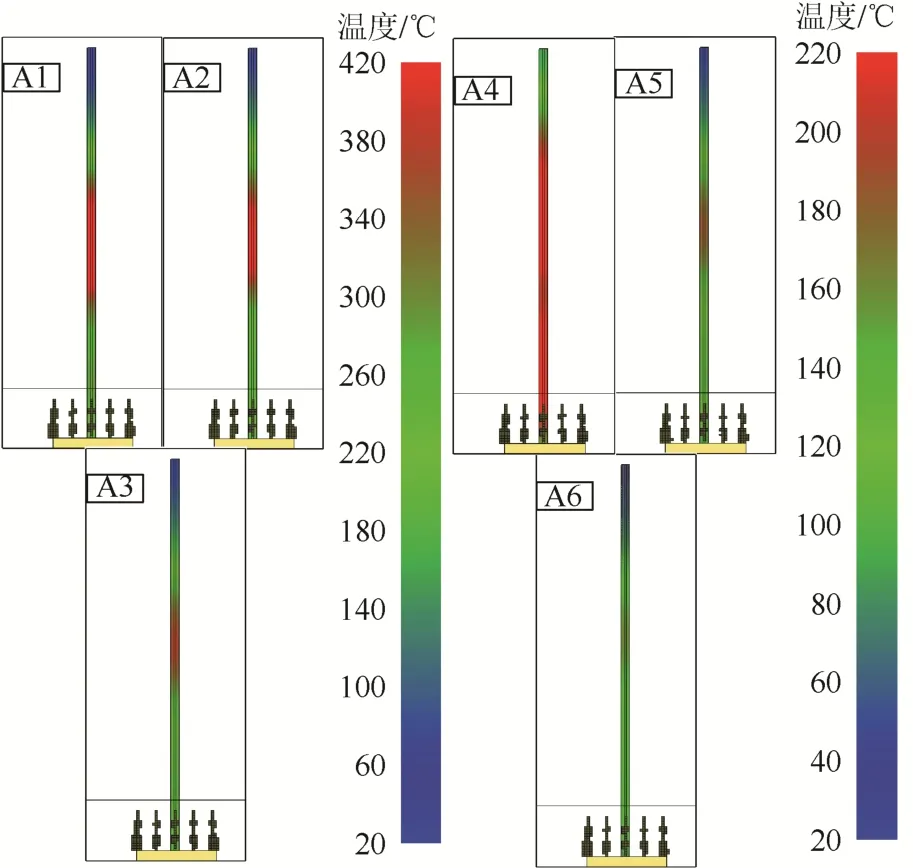
图6 火灾高峰时主材温度分布规律Fig. 6 Temperature distribution law of the main material during fire peak

图7 各火灾场景主材最高温度Fig. 7 Maximum main material temperature of each fire scene
从图6可以看出:A1—A3火灾场景下,主材最高温度为420 ℃。A4—A6火灾场景下,最高温度为220 ℃,并且主材温度均呈中间高、两边底分布规律;随着距离增大,高温区呈逐渐减小的趋势。
从图7中可以看出:对于A1—A5火灾场景,当主材距离火场分别为12 m、13 m、14 m、15 m、16 m,主材50 m高度以下时,主材钢管温度随着高度的增加呈增大趋势;超过50 m后,温度迅速降低。以A1火灾场景为例,主材钢管温度从开始的313 ℃逐渐增大到566 ℃;之后随着高度的增大迅速下降到123 ℃。A2—A5火灾场景与A1场景变化规律基本类似。对于A6火灾场景,当主材距离火场为 17 m时,主材钢管温度从开始的252 ℃逐渐增大到267 ℃,之后随着高度的增大迅速下降到143 ℃。由此可见,随着主材与火场距离的增加,主材最高温度不断降低,主材距离火场12 m时,主材的温度峰值最大,温度值为568 ℃。对于各火灾场景,在主材高度0~50 m区间段,温度逐渐上升;在50 m~80 m之间时,主材温度迅速下降。主材最高温度峰值均位于50 m附近。
3.3 钢管塔主材安全距离判定
考虑到输电铁塔在设计时,其主材构件强度利用率一般均在0.9左右,所以本文以“屈服强度折减系数在0.9以下”作为主材失效的判定准则。
利用式(2)计算屈服强度折减系数。折减系数等于1,说明主材没有受到高温影响;折减系数小于1且大于0.9,说明主材屈服强度发生变化,但是满足强度设计要求;折减系数小于0.9,说明主材局部可能发生屈服变形失效。
图8示出了主材于不同高度的屈服强度折减系数计算结果。从图8可以看出,在不同火灾场景下,最小屈服强度折减系数出现位置基本相同:最小值均出现在50 m高度附近。因此,主材距离地面50 m高度是有可能最先发生失效的位置。

图8 主材于不同高度屈服强度折减系数Fig. 8 Reduction coefficient of yield strength of different heights
图9示出了不同火灾场景下,主材最大屈服强度折减系数计算结果。从图9中可以看出:随着主材与火场距离的增大,其屈服强度折减系数也逐渐增大。主材距离火场12 m~14 m时,主材的屈服折减系数分别为0.54、0.64、0.88;15 m~17 m时,主材的屈服折减系数分别为0.93、0.99、1。由此可见,主材距离火场12 m~14 m时,主材局部可能会发生屈服变形失效;15 m~16 m时,主材虽然满足使用标准,但是受到高温影响屈服强度发生折减,力学性能发生改变;17 m时,主材强度在高温作用下和无火作用相比没有变化。综上所述,15 m为最小安全距离。
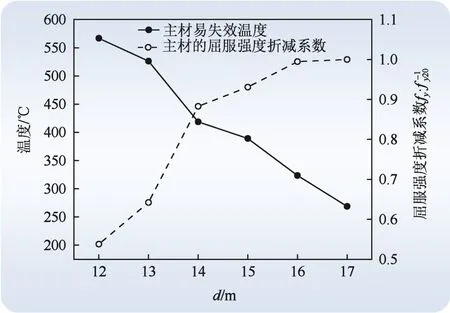
图9 不同火场距离下屈服强度折减系数Fig. 9 Reduction coefficient of yield strength at different fire distances
4 结论
本文通过仿真建模,研究了在森林火场与主材不同距离条件下,特高压钢管塔机械强度变化情况,得到结论如下。
(1)当主材距离火场12 m、13 m、14 m、15 m时,其屈服强度分别下降了46%、36%、12%、7%。在主材距火场由14 m过渡到13 m的过程中,屈服强度下降变化幅度较大。
(2)对于各火灾场景,主材温度的变化趋势相同:在主材50 m高度以下位置,主材钢管温度随着高度的增加呈增大趋势;超过50 m后,温度迅速降低,在40 m~50 m之间取得峰值。
(3)当主材与火场距离在14 m以内时,主材局部会发生屈服变形失效,失效位置位于距离地面50 m高度附近;距离大于15 m时,受到高温影响,材料屈服强度会发生折减,但仍满足标准要求。故最小安全距离为15 m。
