分时电价下电动汽车有序充放电优化策略
2023-03-03包宁宁刘晓波
包宁宁,刘晓波
(贵州大学 电气工程学院,贵州 贵阳 550000)
0 引言
随着电动汽车(Electric vehicles,EV)保有量的不断增加,其充电功率会对现有电网的运行造成一定程度的影响[1],比如网络损耗增大[2]、供电可靠性降低[3]等。文献[4]的研究表明,EV的充电时段与居民生活用电时段存在重合,这可能会导致电网负荷“峰上加峰”的情况发生。因此,为降低 EV充电负荷对配电网运行造成的负面影响,对EV充放电策略进行研究具有实际意义。
迄今为止,在 EV接入电网方面,已有相关研究做出了诸多富有开拓性和实用性的贡献。文献[5]提出了针对 EV充电功率需求的统计学建模方法。文献[6]从不同角度提出了 EV充电优化调度方法。文献[7]提出了2种EV负荷聚集商调度策略——固定签约策略及灵活签约策略。文献[8]构建了汽车出行链,通过研究得到了不同优化调度策略的应用效果。文献[9]基于一致性K均值聚类进行了EV充电负荷建模。文献[10]利用模糊算法计算了不同情况下用户充电概率,构建了包含纯 EV充电电价引导层与综合能源系统交互策略能量调度层的双层能量调度模型。文献[11]通过引入双层优化,即发电侧(热能和风能)优化和配电侧(EV充放电)优化,建立了风力发电预测模型以及实时电价模型。文献[12]考虑电网公司对缩小峰谷差的奖励,提出了2阶段优化模型。文献[13]结合每台 EV接入的时间及实时峰谷电价,分 2阶段对 EV的充电行为进行引导;通过引入虚拟荷电状态,实现了对充放电系数的修正;该方法有利于用户对充电行为进行决策。
目前相关研究中所提出的 EV有序充放电策略,还不能最大化地开发 EV削峰填谷的潜力、满足用户的经济期望。
鉴于此,本文根据分时电价规定了充电时段、放电时段,并在此基础上提出在最大化开发利用EV削峰填谷潜力,同时满足用户经济性要求的优化策略。
1 EV充电需求建模
以住宅小区中 EV充放电负荷调度优化为研究对象。将小区内全部 EV充放电负荷考虑为配电网中的1个节点负荷,从整体的角度研究其参与配电网负荷调度相关工况;重点分析在分时电价的条件下其与配电网的互动调度。
在EV参与下,EV不但可以作为负荷参与到配电网中,还可以作为电源在负荷高峰时为电网提供能量[14]。
EV充电需求主要由3个因素决定:充电开始时的电池状态(初始ESOC)、充电开始时刻(汽车到达时刻)、充电结束时刻(汽车离开时刻)。
根据文献[15],EV到达时刻的概率密度函数满足正态分布:
式中:σs=3.4;μs=17.6。
EV日行驶距离满足对数正态分布,其概率密度函数为:
式中:σD= 0 .88;μD=3.20;xD为EV日行驶距离。
EV在行驶过程中所耗费的电能与其行驶距离成正比关系,因此可以由 EV的日行驶距离得到电动汽车的初始ESOC:
EV的充电时长为:
式中:t为充电时长;PC为充电功率;为EV充电目标值;φ为充电效率。
2 EV有序充电优化策略模型
2.1 目标函数
EV循环充电会带来电池损耗。因此,在计算成本时,应考虑电池的损耗。
根据文献[16],电池退化成本可表示为:
由式(5)可知,当EV放电时,将会产生电池损耗费用;当EV充电时,不会产生电池损耗费用。
当 EV放电时,将会产生电池损耗费用;当EV充电时,不会产生电池损耗费用。
考虑到用户参与有序充电主要原因是关注成本经济性,因此把有序充电成本最小作为目标函数:
式中:F1为考虑电池损耗后的EV充放电成本;xt为电池状态;St为t时段的充放电电价;Sp、Sf、Sv分别为峰时段、平时段、谷时段充电电价。为方便计算,假定充电电价等于放电电价。
当xt=1时,电池处于充电状态;xt=0时,电池处于静默状态;当xt= –1时,电池处于放电状态。
由于低电价会对充电方式造成影响,所以在低电价时段可能会出现新的负荷尖峰。因此,在低电价时段,将 EV充电所造成的配电网负荷曲线波动做为主要考虑因素,把负荷曲线波动最小做为目标函数:
式中:Pe,t为t时刻EV集群参与充电时的总功率;PL,t为t时刻原配电网的基础负荷。
为了满足用户充电成本最小化以及平抑负荷曲线波动的目的,将目标函数F1、Ht利用线性加权法进行规范化处理:
式中:ft为多目标优化函数;分别为目标函数F1、Ht的最大值;α1、α2分别为目标函数F1、Ht的优化权重。
2.2 约束条件
2.2.1 充放电功率约束
式中:PC为EV充电功率;PC,max为EV充电功率允许最大值;PD为EV放电功率;PD,max为EV放电功率允许最大值。
2.2.2 电池可用容量约束
EV蓄电池的使用寿命与放电深度和循环次数有关。为了延长电池的使用寿命,对电池充放电时的电池容量进行约束:
为保证电池的健康状态,其可用容量的上、下限一般取0.9、0.2。
2.2.3 用户期望电量约束
为了满足用户的日常出行需求,当 EV离开电网时,其电量状态应该满足以下约束:
3 EV充放电控制策略
EV充放电控制总流程如图1所示。
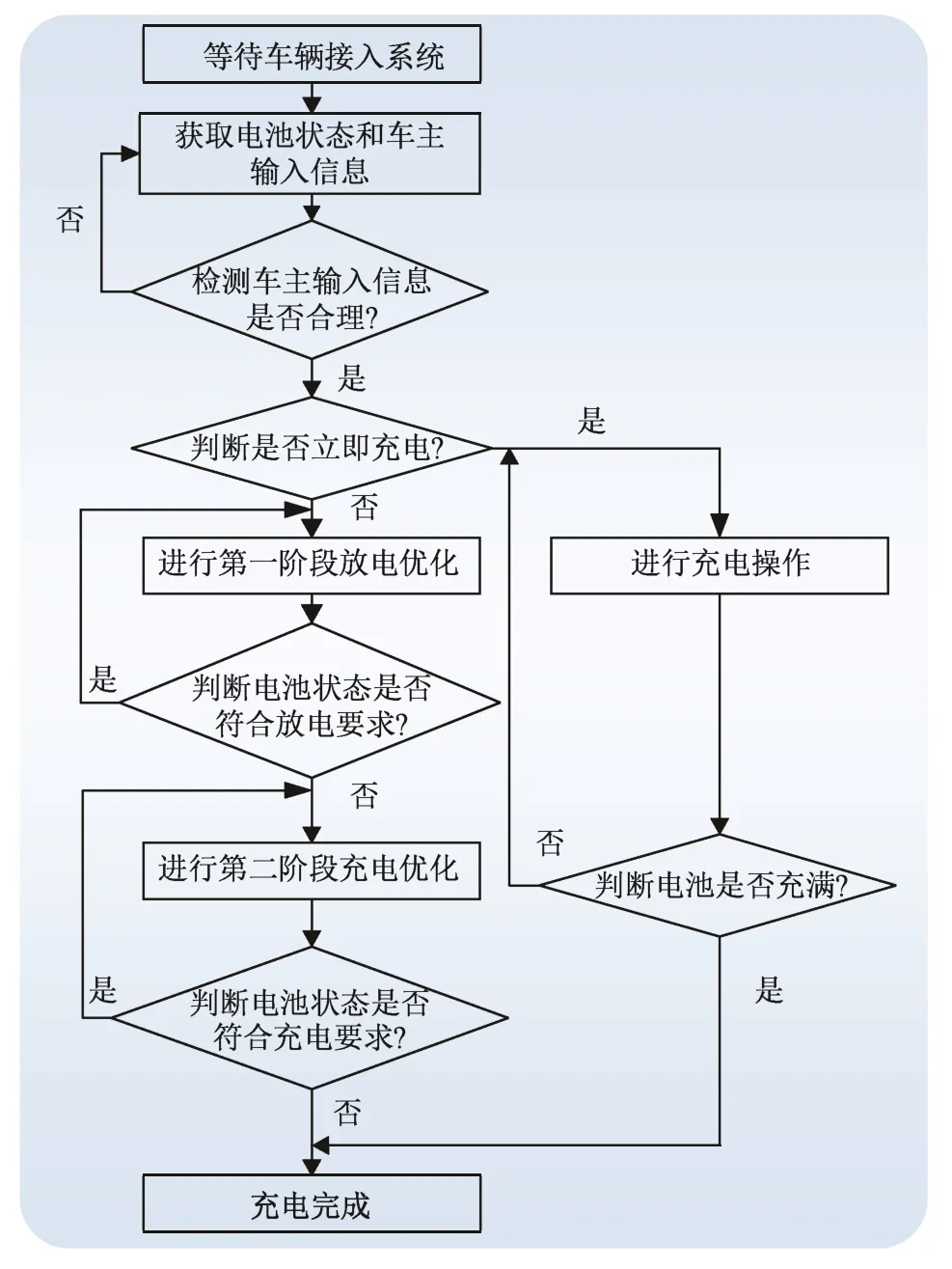
图1 充放电控制总流程Fig. 1 Flow chart of the charging and discharging control
由图1可知,当第i辆EV接入配电网时,系统获取该车辆的电池容量以及初始值ESOC值,并记录车辆接入系统的时间tin。为了更好满足用户的充电需求,用户需要输入退出充电时间tout、期望的电池以及是否要响应充放电优化策略。
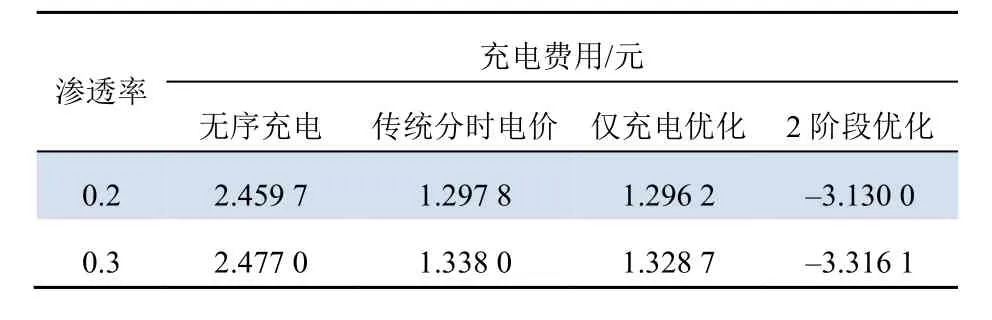
EV的停车时长tp与充电时长t的关系有2种:当tp>t时,该车辆满足有序充放电条件,系统可以安排该EV进行充放电优化;当tp PSO是一种基于进化理论的计算方法。该算法可以有效地解决复杂的优化问题,广泛应用于电力系统问题求解过程中。 PSO基本原理:每个粒子拥有自己的位置和速度,还有1个由目标函数决定的适应值。任何粒子都知道到目前为止发现的最佳位置(Pbest)及其当前位置。此外,所有粒子也知道到目前为止整个群体所有粒子的最佳位置(Gbest)。粒子i的位置被表示为Xi= (Xi1,Xi2,···,XiD),粒子i的速度被表示为Vi= (Vi1,Vi2,···,ViD);速度和位置更新方程为: 当EV车辆i满足有序充放电的条件时,系统首先安排该EV在峰时段进行第一阶段有序放电,具体流程如下。 (1)将每个时段接入电网的 EV按照ESOC的大小进行降序排序。 (2)利用PSO算法以式(8)为目标函数对参与放电的 EV数量进行优化,得出参与优化的EV数量n。 (3)选择参与排序的前n辆EV进行放电,并结合式(10)更新EV的ESOC值。 第二阶段充电优化流程如下。 (1)将每个时段接入电网的 EV按照ESOC的大小进行升序排序。 (2)利用粒子群优化算法以式(8)为目标函数对参与放电的 EV数量进行优化,得出参与优化的EV数量n。 (3)选择参与排序的前n辆EV进行放电,并结合式(10)更新EV的ESOC。 参考目前市场上的主流 EV型号并考虑到未来电动汽车技术的进步,本文对 EV仿真参数做出如下假设:EV电池为锂电池,其额定容量为32 kW∙h;额定充电功率为7 kW,充电效率为90%;用户期望ESOC为90%;EV接入电网时间以及日行驶里程符合概率密度分布,EV每100 km耗电量为15 kW·h。将多目标优化函数中目标函数F1、Ht的优化权重α1、α2分别设置为 0.5,0.5(可合理调整)。 以如表1所示,以某居民区的基础负荷为算例。经过拟合,得到本文所用的基础负荷数据。 表1 某居民区基础负荷表Tab. 1 Foundation load of a residential area 电网电价采用国内工业用电分时电价,具体参数如表2所示。 表2 分时电价参数设置Tab. 2 Parameter setting of time-of-use tariff 在 EV占全部汽车数量比例(渗透率)分别为0.2和0.3条件下,利用蒙特卡罗方法模拟电动汽车集群在24 h内充放电情况,并分析该小区居民在本文所提的优化策略(仅充电和充放电)、无序充电和传统分时电价这4种充电方式下的充电结果。 计算时,本文策略以及传统分时电价采用的电价数值为上表电价数值,无序充电电价数值为分时电价的平均值。 (1)无序充电方式。 在这种方式下,假定所有的 EV在接入电网后立即开始充电,直到电池荷电状态达到 90%以上或者达到车主设定状态。 无序充电方式仿真结果如图2所示。由图2可知,该充电方式会加大电网的负荷峰值,使电网的峰谷差变大。 图2 无序充电仿真结果Fig. 2 Simulation results of disordered charging (2)传统分时电价方式。 在此种方式下,尽量安排 EV在谷时段进行充电操作。传统分时电价方式控制流程如图3所示,具体仿真结果如图4所示。 图3 传统分时电价策略控制流程Fig. 3 Flow chart of traditional TOU price strategy 图4 传统分时电价仿真结果Fig. 4 Simulation results of traditional TOU price strategy (3)仅充电优化。 该方式下负荷曲线如图5所示。从图5中可以看出,在峰时段时,EV不参与放电;在谷时段,EV进行充电,降低了负荷曲线峰谷差。 图5 充电优化仿真结果Fig. 5 Simulation results of charging optimization (4)充放电的2阶段优化。 通过 2阶段充电优化所得的负荷曲线如图6所示。在峰时段时,EV参与放电,大大降低了峰时段的负荷峰值;在谷时段,EV进行充电,提高了谷时段的负荷,大大降低了负荷曲线峰谷差。 图6 充放电2阶段优化仿真结果Fig. 6 Simulation results of two-stage optimization of charging and discharging 各充电模式的峰谷差以及充电费用对比结果分别如表3、4所示。 表3 各优化充电模式产生的峰谷差对比Tab. 3 Comparison of peak valley difference generated by four optimized charging modes 表4 各优化充电模式产生的充电费用对比Tab. 4 Comparison of charging costs generated by four optimized charging modes 由表3可知,无序充电所造成的峰谷差最大,有序充电其次。充放电的2阶段优化所形成的峰谷差最小。随着渗透率的增加,2阶段优化模型的优势也越来越明显。该结果表明,应用2阶段优化模型可以提高配电网运行的稳定性。 从表4可知,无序充电所需充电费用最高,2阶段优化策略所需充电费用最低,甚至可以带来额外的放电收益。 针对 EV无序充电方式以及传统有序充电模式可能会造成新的负荷尖峰的问题,本文提出了2阶段优化的解决策略。计算结果表明,采用本文所提策略,不但可以使 EV用户充电费用最低,还可以使 EV用户利用该策略得到一定的收益;随着EV渗透率的提高,收益也随之变高。 EV渗透率为 0.2时,无序充电的峰谷差为36.5 MW,应用本文方法后降至24.6 MW;这结果表明,应用本文策略可以缓解电网的运行压力。 综上,无序充电、传统有序充电、仅充电优化以及本文 2阶段充放电优化策略的对比结果表明,本文提出的 2阶段充放电优化策略可行、有效。3.1 PSO算法
3.2 第一阶段——放电优化
3.3 第二阶段——充电优化
4 算例分析
4.1 参数设置
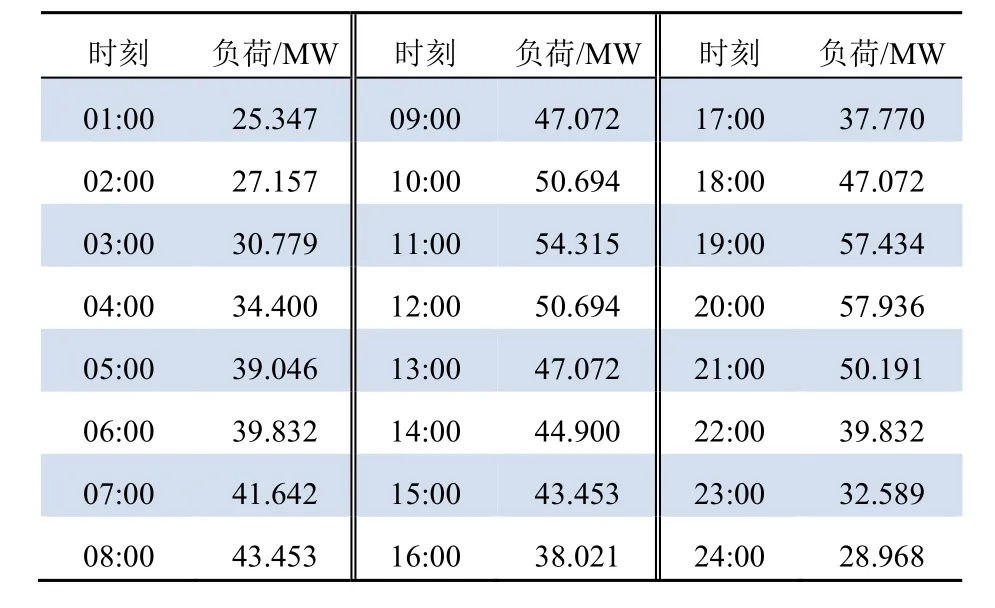

4.2 仿真结果


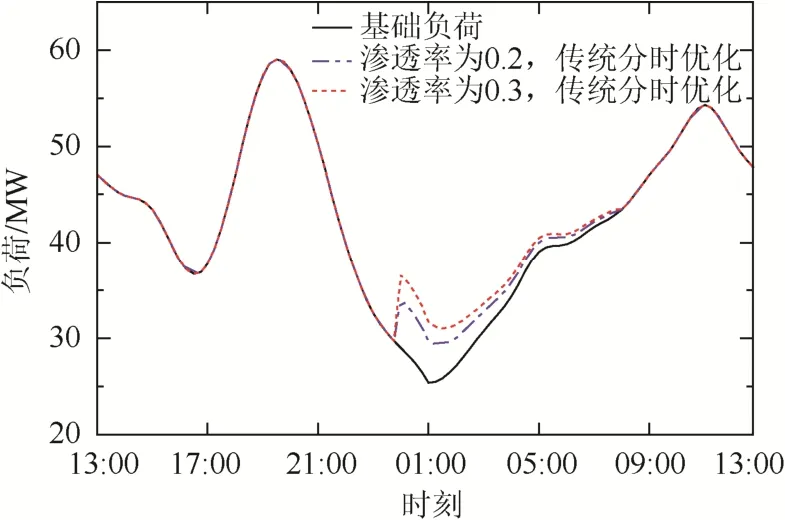
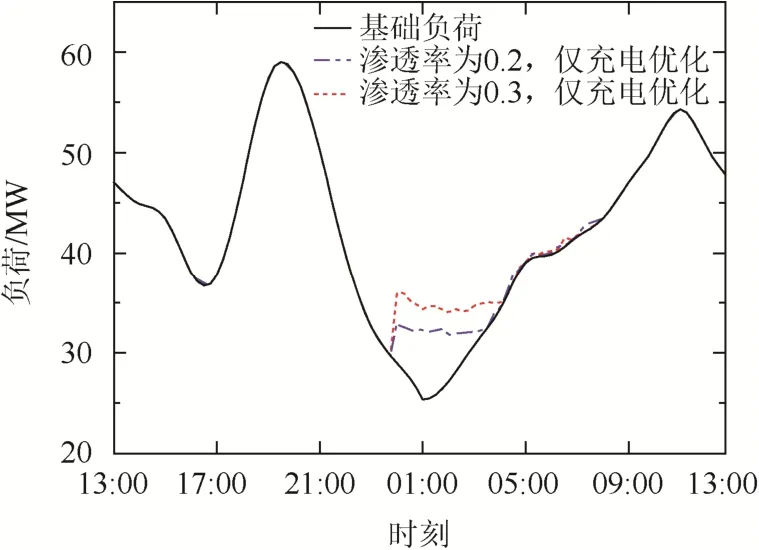


5 结论
