基于BWOA-GAM-BiGRU的火电厂SCR系统出口NOx排放预测
2023-03-03马永光郭浩宇
马永光,郭浩宇
(华北电力大学 自动化系,河北 保定 071003)
0 引言
燃煤电厂是氮氧化物(NOx)等大气污染物的重要排放源之一。在燃煤电厂生产过程中,目前广泛使用选择性催化还原(Selective catalytic reduction,SCR)方法来降低 NOx的排放。SCR反应过程具有大延迟、大惯性、非线性特点,且NOx浓度测量设备也存在一定的时间延迟;这导致喷氨量无法迅速调整以匹配NOx浓度变化[1]。
因涉及复杂的内部机理过程,使用传统的机理分析建模方法很难建立一个准确的模型来描述对象间的非线性关系。随着数据驱动建模与人工智能方法的成熟,越来越多的研究者将解决该问题的思路转向智能建模领域[2]。
文献[3]设计了基于弹性网络(Elastic net)与最小二乘支持向量机(Least squares support vector machine,LSSVM)的SCR出口NOx预测模型,用Elastic net对特征变量进行选择,用LSSVM进行预测。相比传统LSSVM,该模型预测误差减少8.45%,但测试集的均方根误差(Root mean square error,RMSE)仍高达 7.555 8;所以,模型预测精度有待进一步提高。
文献[4]使用深度循环神经网络(Deep recurrent neural network,DRNN)结合长短期记忆(Long short-term memory,LSTM)的 DRNNLSTM模型预测SCR出口NOx排放量。所建立的模型虽然取得了较高的预测精度,但是该模型只能利用序列数据单一方向的信息,且未考虑特征变量的时延特性。
文献[5]提出了一种含有多层结构的深度双向LSTM 模型。相较其他模型,该模型预测误差下降了5%,模型泛化能力好;但该模型结构较为复杂,同样未考虑特征变量的时延特性。
注意力机制(Attention mechanism,AM)[6]通过对模型的输入特征赋予不同的权重的方法来突出关键影响因素[7],进而辅助模型做出准确的判断。
文献[8]针对航空发动机剩余寿命预测,使用了基于特征注意力机制并融合生成对抗网络(Generative adversarial network,GAN)与门控循环单元(Gated recurrent unit,GRU)网络的混合模型,得到了比传统模型更高的预测精度。
文献[9]建立了一种结合时序注意力机制与LSTM 的混合预测模型 AM-LSTM。所建立的模型预测精度高,泛化能力强。
文献[10]使用含有特征注意力和时序注意力的双注意力机制,并结合GRU网络,对电力短期负荷进行预测。与其他多种模型对比结果表明,所提出的模型预测精度最高。
虽然注意力机制在文本处理、机器翻译、负荷预测等诸多领域取得了广泛应用,但是其应用于火电生产领域的相关研究较少。另外,在上述研究中,几乎所有深度神经网络模型最优超参数都是靠经验手动设置的,所以模型具有很强的主观性,未能实现模型性能最大化。
针对以上问题,结合SCR出口NOx排放预测,本文提出一种基于数据驱动且充分考虑变量时延特性的、结合了全局注意力机制(Global attention mechanism,GAM)与双向门控循环单元(Bidirectional gated recurrent unit,BiGRU)深度神经网络的模型:充分利用BiGRU可以深度挖掘数据序列前后2个方向的时间依赖特性能力,以及 GAM 可以自动分配神经元隐藏状态输出权重的优势,突出重要信息的影响作用,从而提高模型预测精度;采用正则化技术(Dropout)与Adam结合的优化算法来提高模型收敛速度并防止过拟合;使用黑寡妇优化算法(Black widow optimization algorithm,BWOA)对超参数进行自动寻优,以克服网络超参数依靠个人经验手动调整带来的不利影响,最大程度发挥模型的性能,提高预测精度。
1 模型原理
1.1 GRU网络
GRU是LSTM的一种简化结构,是一种专门用来处理时间序列的循环神经网络(Recurrent neural network,RNN)。GRU内部只有更新门和重置门 2个门结构,在保持了 LSTM效果的同时,又具有比 LSTM 有更少的参数和更好的收敛性的优势[11]。GRU网络神经元细胞结构如图1所示。

图1 GRU神经元结构图Fig. 1 Neuron structure diagram of GRU
GRU网络具体计算过程如下:
式中:xt为当前时刻输入;ht–1为神经元上一时刻隐状态;rt和zt分别为当前时刻重置门和更新门的输出;W为权重矩阵;b为偏置项矩阵;为神经元当前时刻候选隐状态;ht为当前时刻最终状态输出;“⊗”表示矩阵对应元素相乘;tanh和sigmoid为激活函数。
1.2 BiGRU网络
BiGRU对传统GRU网络进行了改进。BiGRU由2层方向相反的GRU网络组成,可以获取序列数据前后2个方向的信息。BiGRU网络结构如图2所示。

图2 BiGRU结构图Fig. 2 Structure diagram of BiGRU
1.3 GAM
与 Bahdanau注意力机制相比,GAM[12]的结构设计更加合理,其评分函数也进行了扩展:在经典编码器–解码器(Encoder-decoder)结构基础上构造一个注意力层(Attention layer),通过计算神经元历史隐藏状态与当前时刻隐藏状态之间的关联程度,将更多的注意权重分配到关联程度大的部分,从而实现对数据特征的自适应关注。
GAM计算过程如下:
式中:ats为历史时刻(s时刻)神经元输出隐状态对当前时刻(t时刻)输出的注意力权重;score为评分函数;是神经元历史输出隐状态;ht是神经元当前时刻输出隐状态;ct是中间变量;是经注意力加权计算后的神经元当前时刻最终输出。
1.4 黑寡妇优化算法
BWOA[13]模拟了黑寡妇蜘蛛的繁殖行为。相比于其他优化算法,该算法在寻找全局最优解时收敛速度更快、精度更高。BWOA计算步骤为:
(1)初始化。确定黑寡妇蜘蛛(均为雌性蜘蛛)种群数量、最大迭代次数,确定每只黑寡妇蜘蛛代表的待优化参数数量及范围,确定适应度函数。
(2)位置更新。根据适应度函数值确定当前最优黑寡妇蜘蛛位置,之后进行位置更新。黑寡妇蜘蛛在网格内按照线性和螺旋2种方式进行运动,位置更新如(9)式所示。
式中:Xi(t+ 1 )为更新后的黑寡妇蜘蛛位置;Xbest为当前最优黑寡妇位置;m为[0.4,0.9]区间的随机数;β为[–1,1]区间的随机数;rand为[0,1]区间的随机数;Xr1(t)为随机选择的种群内第r1个黑寡妇的位置;Xi(t)为当前黑寡妇蜘蛛位置。
(3)计算信息素。如式(10)所示。信息素在蜘蛛的求偶过程中起着非常重要的作用。当信息素值等于或小于0.3时,代表该雌性黑寡妇蜘蛛是饥饿的蜘蛛(雌性蜘蛛会吃掉雄性蜘蛛)。求偶过程中它将不会被雄性选中,但将被另一个雌性蜘蛛取代。按式(11)更新此时黑寡妇蜘蛛位置。
式中:ph(i)为第i个黑寡妇蜘蛛信息素;fitmax和fitmin分别为最优和最差适应度函数值;fit(i)为第i个黑寡妇蜘蛛适应度值;Xi(t)为低信息素值黑寡妇蜘蛛的位置;r1和r2为种群数量内的随机数(r1≠r2);Xr1和Xr2分别为第r1和r2个黑寡妇位置;σ为随机二进制数,为0或1。
(4)重新评估适应度函数值,并更新最优黑寡妇的位置及最优适应度函数值。
(5)重复步骤(2)—(4),进行迭代运算,直到满足停止条件(达到最大迭代次数或允许误差),输出最优黑寡妇位置和最优适应度函数值。
2 数据预处理与变量筛选
原始数据取自某2×300 MW火电厂分散控制系统(Distributed control system,DCS)连续7 d的运行历史数据,涵盖高、中、低负荷范围。数据样本共10 080条,采样间隔1 min。
2.1 数据清洗
数据驱动建模对数据精度十分敏感,对数据品质有较高的要求。建模之前首先对数据进行清洗,以消除其对模型精度的影响。
对于离群值,本文使用箱线图(Box-whisker plot)方法进行筛选,然后使用均值填充法对异常值进行修正。箱线图结构如图3所示。

图3 箱线图结构Fig. 3 Structure diagram of box-whisker plot
根据图3,箱线图法计算步骤如下:
(1)计算上四分位数(Q3)、中位数、下四分位数(Q1)。
(2)计算四分位距(Interquartile range,IQR),即:IQR=Q3–Q1。
(3)介于Q1–3IQR与Q3+3IQR之间的数为可接受数值,范围之外的数据划为离群值。
以SCR出口NOx浓度为例,经箱线图法筛选后,离群值分布情况如图4所示。

图4 SCR出口NOx浓度离群值分布Fig. 4 Distribution of NOxconcentration outliers at SCR outlet
本文采用小波半软阈值去噪算法,解决硬阈值去噪带来的信号局部抖动以及软阈值去噪峰值信噪比低的问题。
去噪过程为:首先对原始信号进行小波多尺度分解,得到各尺度系数;对得到的小波系数进行阈值处理;经小波逆变换重构,得到平滑且误差小的信号。
本文采用Mallat算法,以db3小波作为母波,对原始信号进行3层分解,得到1个近似分量和3个细节分量。半软阈值函数f(x)及阈值λ选择为:
式中:N为信号长度。
3种去噪方法的NOx测量信号信噪比(Signalto-noise ratio,SNR)对比结果如表1所示。

表1 SNR对比Tab. 1 SNR comparison
由表1可以看出,使用半软阈值去噪后的SNR值最大,去噪效果最好。
NOx测量信号去噪前后时域波形对比如图5所示。
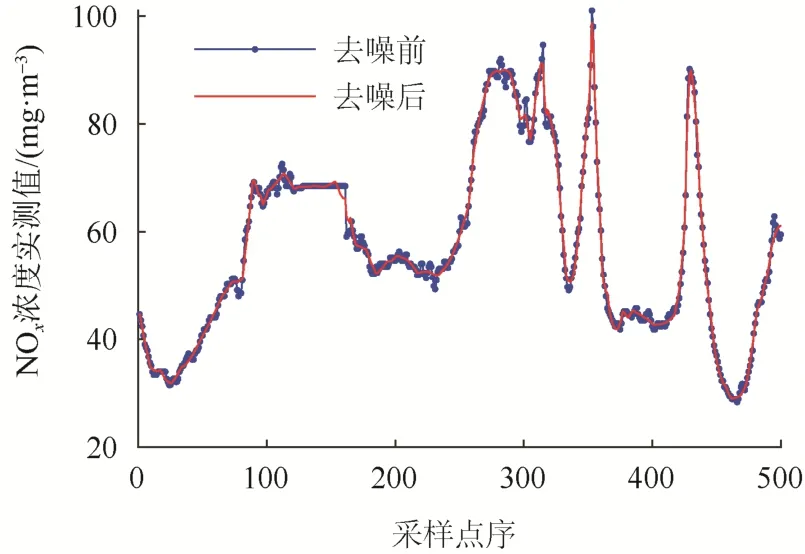
图5 NOx测量信号去噪前后对比Fig. 5 Comparison of NOxmeasurement signal before and after denoising
各个变量量纲的不同,在去除异常值和噪声后,还要对数据进行标准化处理,将其转化为无量纲的表达式。
本文使用Z-Score方法对数据进行标准化。

式中:μ为数据样本均值;σ为标准差;x为原数据;x′为标准化数据。
2.2 变量筛选与延迟时间估计
在对原始数据进行处理后,通过对SCR系统运行机理分析并结合现场人员的实际经验,共找出7个影响SCR出口NOx排放量的主要因素,将其作为模型输入变量。
另外,由于SCR催化还原反应过程缓慢,且各个输入特征变量的测量和NOx测量值之间存在不同的时间延迟,所以DCS记录的同一时刻运行数据中的各相关参数之间未形成准确对应关系[14]。因此,建模之前还需要校准输入变量与输出 NOx之间的时间延迟。
基于信息熵理论,利用互信息(Mutual information,MI)可找出2个随机变量之间的关联程度。离散随机变量X与Y之间的互信息为:
式中:p(x,y)为X与Y的联合概率分布;p(x),p(y)分别为X与Y的边缘概率分布。
设输入变量矩阵为X(t),有:
式中:n为X(t)维度,即变量个数。
令 SCR系统出口 NOx排放量为输出Y(t),τi∈[τmin, τmax]为变量Xi(t)与Y(t)之间的时间迟延,i∈(1,n),则X(t)可以重构为:
式中第i个变量xi(t)重构为:
根据 SCR系统实际运行情况,变量延迟时间范围一般在 0~5min之间。考虑采样周期为 1 min,因此选择τmin=0 min,τmax=5 min。为了求出每个输入变量X(t)的最佳延迟时间,计算过程为:
(1)分别计算式(19)中等号右侧矩阵每一列与输出Y(t)之间的互信息值,其中互信息值最大的那一列对应的τ就是该变量的延迟时间估计。
(2)重复步骤(1)得到所有变量的延迟时间。
输入变量的延迟时间计算如表2所示。

表2 变量延迟时间估计Tab. 2 Estimation of variable delay time
在得到各输入变量的时间延迟后,对原始数据序列进行重构,实现输入变量与输出NOx之间在时间维度上的对齐。
为了进一步提高模型预测的准确性,考虑到数据序列的时间依赖特性,在所选7个变量历史时刻数据的基础上,又加入了SCR出口NOx排放量历史时刻数据。以这8个变量的历史时刻数据形成模型最终输入,输出为未来时刻(未来1个采样间隔)SCR出口NOx排放量。
3 模型构建
3.1 BWOA-GAM-BiGRU模型结构
BWOA-GAM-BiGRU模型结构如图6所示。参数优化与预测输出具体步骤为:

图6 BWOA-GAM-BiGRU结构图Fig. 6 Structure diagram of BWOA-BiGRU
步骤1:初始化黑寡妇种群数量,最大迭代次数;设定网络学习率l、隐层神经元数量k、小批量值b、Dropout系数d这4个参数取值范围。在所设定范围内,随机初始化种群内黑寡妇蜘蛛位置X= [l,k,b,d]。
步骤2:将原始数据进行预处理并按照一定比例划分训练集、验证集、测试集。训练集数据用于更新GAM-BiGRU网络连接权重;用验证集通过训练好的网络进行预测;将预测输出均方根误差(Root mean square error,RMSE)作为 BWOA适应度函数,优化目标为寻找最优超参数值使RMSE值最小。在循环停止条件中,设定允许误差的大小。
步骤3:根据RMSE大小确定初始种群最优黑寡妇位置,然后开始迭代运算。使用式(9)更新黑寡妇位置,使用式(10)计算信息素,使用式(11)更新低信息素黑寡妇位置;然后,重新评估RMSE值,确定此时最优黑寡妇位置,重复迭代,直到满足循环停止条件(达到最大迭代次数或满足允许误差)。
步骤4:达到循环停止条件后,输出的最优黑寡妇位置Xbest即为所求超参数最优值。
步骤5:将得到的4个网络超参数最优值重新输入GAM-BiGRU网络。用“步骤2”中训练集数据训练网络,用测试集数据测试模型最终预测能力。
3.2 模型参数设置
本文实验环境为MATLAB R2020b。BWOA优化过程参数及GAM-BiGRU网络待优化参数取值设置如表3所示。

表3 模型参数设置Tab. 3 Settings of model parameters
4 实验对比
4.1 数据集划分
选择清洗后的数据前10 000组作为最终建模数据。训练集、验证集、测试集划分比例为7:2:1。
4.2 评价指标
为了定量分析模型的预测能力,本文选择对称平均绝对百分比误差(Symmetric mean absolute percentage error,SMAPE)、RMSE、决定系数(R-square,R2)作为检验模型准确性的评价指标。
4.3 实验结果与分析
使用BWOA对GAM-BiGRU网络超参数寻优,得到最优超参数值如表4所示。

表4 最优超参数计算结果Tab. 4 Calculation results of best hyperparameters
表4中,用BWOA优化算法得到的“小批量大小”为模型输入数据的时间段最优值,含义为“模型采用输入变量的前6个时刻对NOx排放量进行预测”。
BWOA-GAM-BiGRU模型预测结果如图7所示。为了更好地说明所提出模型的有效性,使用相同实验数据,选择另外3个典型预测模型即BP神经网络(BPNN)、BiGRU、卷积长短期记忆神经网络(CNN-LSTM)进行对比实验,结果如图8所示。
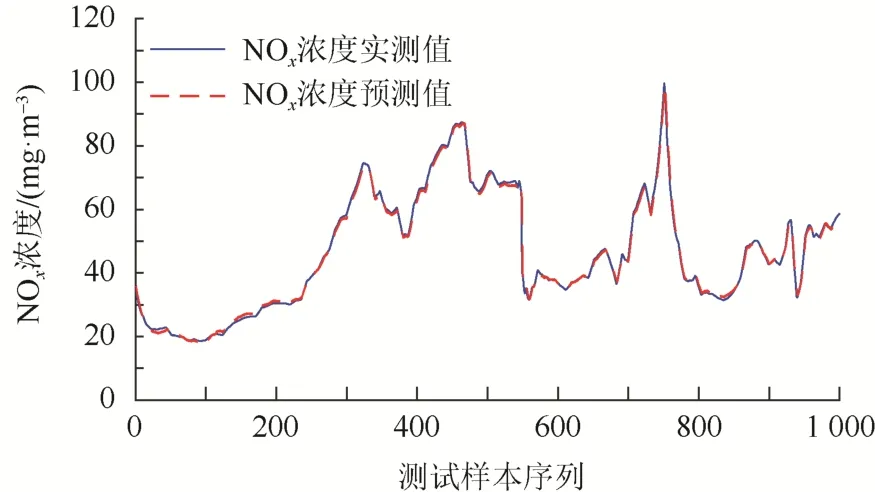
图7 BWOA-GAM-BiGRU预测结果Fig. 7 Prediction results of BWOA-GAM-BiGRU

图8 各模型预测结果对比Fig. 8 Comparison of prediction results of four models
各模型的量化评价指标对比如表5所示。

表5 模型评价指标对比Tab. 5 Comparison of model evaluation indexes
图7中,BWOA-GAM-BiGRU模型NOx预测值与实测值之间差距极小,曲线几乎完全重合。
图8中,BWOA-GAM-BiGRU、BiGRU、CNN-LSTM这3个模型的NOx预测值都可以很好地跟踪实测值变化,且BWOA-GAM-BiGRU模型最贴近实测数据,BPNN相对较差。
表5中,BWOA-GAM-BiGRU的SMAPE和RMSE值最小,这说明该模型的预测精度最高;该模型的R2系数最大,说明该模型的数据跟踪能力最好。
各模型的线性拟合结果,如图9所示。


图9 各模型直线拟合结果对比Fig. 9 Comparison of linear fitting results of four models
由 9可以看出:NOx预测值和实测值构成的散点基本都分布在拟合直线两侧,拟合直线均比较接近理想直线x–y=0;BWOA-GAM-BiGRU模型最接近理想直线;BPNN散点分布较为散乱,拟合效果一般。
5 结论
针对SCR系统大迟延、大惯性的特点,以及现有NOx预测模型超参数依靠手动调节、不能自适应关注重要信息的问题,本文对SCR系统历史数据进行了深度挖掘,估计了变量的时间延迟,提出了一种结合全局注意力机制与BiGRU网络,并使用黑寡妇优化算法对网络参数自动寻优的SCR出口NOx排放预测模型。
实验结果表明,与另外几种典型预测模型相比,所提出模型的预测结果RMSE值仅为1.228,且R2值达到0.996。该预测精度最高,误差最小,说明模型泛化能力最好。
下一步研究方向:对多个时刻NOx排放量进行预测,以检验模型的长期预测能力;根据结果对模型结构进行更深层次的优化,进一步提高模型预测精度。
