基于用电行为特征的工业用户需求响应潜力研究

宋美琴，王俐英，曾 鸣

（华北电力大学 经济与管理学院，北京 昌平 102200）

0 引言

随着电力生产中可再生能源占比不断上升，电网负荷峰谷差持续增加。需求响应是减少峰谷差、维持电网供需平衡的有效手段之一[1]。

针对需求响应潜力测算，国内外学者进行了诸多研究。文献[2]提出了基于深度子领域自适应的需求响应潜力评估方法。文献[3]对居民住宅用电负荷建模，分析了居民建筑参与需求响应的潜力。文献[4]建立了基于中长期时间维度的需求响应系统动力学分析模型。文献[5]将高质量 AP（Affinity propagation）聚类算法引入负荷聚类并进行改进。文献[6]构建了需求响应潜力评估模型，减轻用户需求响应能力差异和响应行为不确定对负荷聚合商响应特性的影响。文献[7]提出一种基于模糊优化集的需求侧用户响应潜力评估方法，建立了潜力评估的量化模型，实现了对用户响应潜力的初步量化。文献[8]采用稀疏编码方法提取调峰潜力特征，建立用电特征与调峰潜力间的映射关系，实现对居民用户的调峰潜力评价。

通过对负荷曲线及相关指标分析，获取用户的用电规律和模式，有利于分析用户的需求响应潜力[9]。文献[10,11]分别采用离散傅立叶变换、多级离散小波变换提取负荷特征指标，减少了电力负荷数据的冗余。文献[12,13]分别提出结合自适应因子与概率统计法特征指标降维与熵权法的日负荷曲线聚类方法，并验证了可行性与优越性。

工业用户在需求响应方面具有较大的潜力[14]，但工业负荷峰谷分布不规律、用电模式与工艺要求紧密度高。基于此，本文收集单个工业用户全年用电数据并提取用电特性指标；考虑到地区和气候对用电行为的影响，分别对大小风季的用电负荷曲线进行聚类分析；引入符合典型用电曲线特性的响应系数进行需求响应的计算。

1 需求响应潜力计算流程

1.1 数据处理

从被调研企业获得全年n条日负荷曲线；每条负荷曲线测量数据时间尺度为1 h，1 d共有24个点，负荷曲线为L=(l0,l1,···,l23)。针对存在缺失的数据，计算前后5个时间点的数据的平均值进行填补，并剔除掉全天负荷为0的曲线。

1.2 计算框架

K-Means聚类方法以簇中的平均值作为质心；K-Mediods聚类方法则以离均值最近的实际点（即数据集中真正存在的最优值）作为质心，误差更小。因此，本文选择K-Mediods聚类方法进行聚类分析，流程如图1所示。

图1 基于K-Medoids聚类的工业用户需求响应潜力计算框架Fig. 1 Computing framework for demand response potential of industrial users based on K-Medoids clustering

2 用户典型日负荷曲线聚类

2.1 负荷特性指标的确定

过多的特征指标会造成数据冗余，对初始数据进行降维。

将日平均负荷、日负荷率、峰谷差率、峰期负荷率、平期负荷率、谷期负荷率和峰时段持续时间这7个典型负荷特性指标作为特征向量。

（1）日平均负荷

即，电力用户日内用电负荷的平均值。

（2）日负荷率

即，日内的平均负荷与最大负荷的比率，用于反映用户用电负荷的变化情况。

式中：rp为日负荷率；pmax为日负荷最大值。

（3）峰谷差率

即，在统计区间内，峰谷差与最高负荷的比值，用以体现电网的调峰水平。

式中：rd为峰谷差率；pmin为日负荷最小值。

（4）峰期负荷率

即，峰期负荷平均值与最高负荷之间的比值，用以体现峰期负荷的变化情况。

式中：re为峰期负荷率；为峰期负荷平均值。

（5）平期负荷率

即，平期负荷平均值与最高负荷之间的比值，用以体现平期负荷的变化情况。

式中：ru为平期负荷率；为平期负荷平均值。

（6）谷期负荷率

即，谷期负荷平均值与最高负荷之间的比值，用以体现谷期负荷的变化情况。

式中：rv为谷期负荷率；为谷期负荷平均值。

（7）峰时段持续时间

即，用户在用电高峰期用电的持续时间，用以反映用户的用电习惯。

式中：T为峰时段持续时间；Tarise为峰时段出现时间；Tdis为峰时段结束时间。

与原24节点数据比较，用7个日负荷指标来表征原始日负荷数据后，数据量减少了70.83%；实现了原始数据的降维，电力用户负荷特征更加清晰。

2.2 K-Mediods聚类分析

（1）构建原始矩阵

假设共有a个样本，每个样本包含b个变量，xij为第i个样本中的第j个变量，原始样本矩阵为：

（2）标准化处理

以极差作为基数，对原始矩阵进行归一化处理：

式中：max(xi)，m in(xi)分别为原始负荷数据最大值和最小值。

（3）聚类步骤

在进行K-Mediods聚类时，通过计算某个样本点和各个初始聚类中心的欧式距离，将样本点划分到最近中心点所属类中。

式中，(yi1,yi2,···,yir)和(yj1,yj2,···,yjr)表示 2 个r维样本数据对象。

计算平方误差准则函数：平方误差SSE越小，表示数据越接近簇中心，聚类效果也就越好。当目标函数SSE收敛时，说明簇中心几乎不再变化。

假设进行聚类的电力负荷特征指标初始数据集为Q(y1,y2,···,ym)，设有k个簇D(D1,D2,···,Dk)，k个聚类中心为o(o1,o2,···,ok)。计算步骤如图2所示。

图2 最终聚类个数计算步骤Fig. 2 Steps to determine the number of final clusters

具体步骤为：

①选取f个对象作为每个Cluster的聚类中心。

②计算其他样本数据与各个聚类中心的距离，将其分到距离最小的类别中。

③随机选择样本点代替中心点，重新计算其到Cluster内每个样本点的欧式距离。用距离最小的样本点替换聚类中心点。

④使用平方误差SSE对聚类效果进行评估。重复②、③，直到各个Cluster重心在某个精度范围内不变化或者达到最大迭代次数，迭代结束。

（4）有效性指标

聚类评价指标分为外部标准和内部标准2种。外部标准通过聚类结果和预期结果的一致性来判断聚类效果的优良。内部标准基于聚类数据评估聚类结果计算单独质量分数，更为客观。本文选择内部评估指数对聚类结果的有效性进行分析。

①邓恩指数（DVI）

DVI为任意2簇类间最短距离与任意簇的类内最大距离之比，计算公式如式（13）所示：

DVI值越大，表明聚类结果的不同类别之间距离越大，同一类别内距离越小。

②轮廓指数（SI）

SI用类内聚合程度和类间离散程度来评估聚类的效果，计算公式如式（14）所示：

式中：A(i)表示从样本i到所有同一聚类中的每个样本的平均距离；B(i)表示从样本i到其他聚类中所有样本的平均距离的最小值。SI越趋近于 1，则内聚度和分离度都相对较优。

③戴维森堡丁指数（DBI）

DBI为任意2个类别聚类的类内平均距离之和与2聚类中心间距之比的最大值，其计算公式如式（15）所示：

式中：wα，wβ分别为2个类别各自的类内平均距离；ρ(wα,wβ)为2类别中心间距。DBI越小则同类别距离较近，不同类别距离较远，聚类效果好。

DBI较SI计算复杂度更小，更直观。DVI更适用于离散点的聚类效果评价。因此，本文采用DBI来评定聚类个数，DBI数值最小时的f值记为k，kmin=2，。

3 工业用户需求响应潜力测算模型

通过实施可中断负荷需求响应可以有效实现削峰填谷，但可中断负荷量与用电模式和生产工艺过程特点紧密相关，最大可中断容量通常为固定数值。对典型行业可调节负荷的相关研究成果显示，多数行业可调节负荷占比在17%～35%[15]。本文取26%作为所研究工业用户的最大可调节负荷占比。

单个工业用户的电力负荷较为规律，但由于受到产业类型影响，不同行业的电力负荷峰谷分布情况不同。用电规律性越高，需求响应潜力越高。根据工业用户的峰谷特性，可将用电曲线类型归纳为迎峰型、高负荷率型和避峰型。如表1所示，设置各用电模式的响应系数[9]。

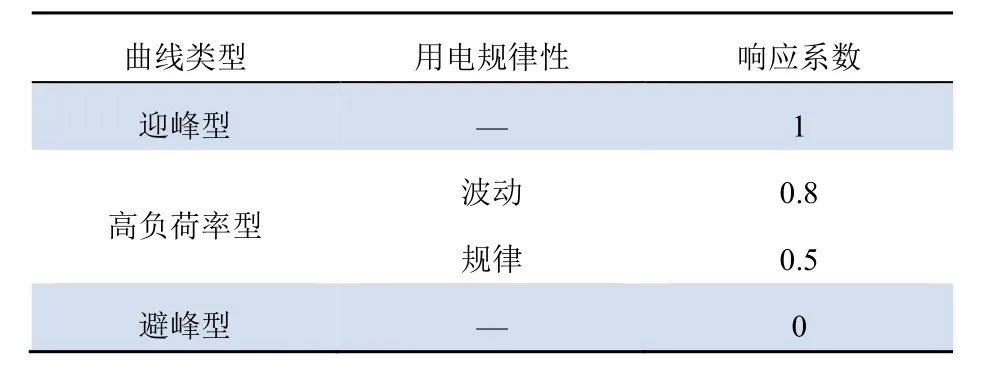
表1 不同类型曲线响应系数Tab. 1 Response coefficient of different types of curves

根据2.2节，得到单个用电用户的k条典型的用电负荷曲线，计算单个用户i的需求响应潜力Pφ：

式中：pc为单个用户某类典型曲线峰时负荷；η为可调节负荷占比系数；ω为负荷曲线的响应系数；T为峰时时长；Xk为聚类后第k类中包含的曲线数量占曲线总数量的比重。

式中：hk为第k类中包含的曲线数量。

地区工业用户需求响应潜力PA为：

4 算例分析

4.1 基础数据

以华北某市区工业用户为算例。调研发现：高耗能行业占全市总负荷比例较大，约为79.5%；商业及其他工业负荷规模约占 8.8%、居民负荷约占11.7%；该市负荷规模呈现递增趋势，全年用电分大小风季。因此，此市区需求侧响应资源主要分布在高耗能行业中。

考虑算例的电力供需情况和季节负荷特性，将1—5月、9—12月划分为大风季，6—8月划分为小风季。结合该地区全网用电特性、新能源发电出力波动和净负荷曲线特点，确定峰、平、谷时段，结果如表2所示。

表2 大、小风的季峰、平、谷时段情况Tab. 2 Peak, flat and valley periods in strong and weak wind seasons

4.2 地区工业用户需求响应潜力

调研10个工业用户历史负荷数据。以用户A的2019年历史负荷数据为例，大小风季日负荷曲线如图3、图4所示。

图3 A用户大风季日负荷曲线Fig. 3 Daily load curves of user A in strong wind season

图4 A用户小风季日负荷曲线Fig. 4 Daily load curves of user A in weak wind season

根据公式（1）—（7），将原数据进行降维处理；根据负荷特性指标将大小风季的日负荷曲线分别聚类，计算DBI指标并确定各自合适的聚类数。通过计算，得到A用户大风季日负荷曲线最佳聚类数k1=4，小风季日负荷曲线最佳聚类数k2=3。得到日负荷样本的聚类曲线，如图5、图6所示。

图5 A用户大风季典型日负荷曲线Fig. 5 Typical daily load curve of user A in strong wind season

图6 A用户小风季典型日负荷曲线Fig. 6 Typical daily load curve of user A in weak wind season

通过对比发现：聚类处理后的电负荷数据规律清晰。除此以外降维前聚类时间为4.332 s，聚类后为1.146 s，为降维前的1/4左右。通过提取负荷特征指标对负荷数据降维，可以提升聚类效果。

根据公式（16）—（19）计算可得：在大风季，A用户的需求响应潜力在大风季为1.58 MW；在小风季的2个峰时段分别为4.19 MW和1.37 MW。10个工业用户需求响应潜力如表3所示。

表3 10个工业用户需求响应潜力结果Tab. 3 Results of demand response potential of 10 industrial users

考察表3数据：该地区工业用户在大风季的总需求响应潜力为20.83 MW，占总用电量的5.3%左右；在小风季2个峰时段的总需求响应分别为36.22 MW和32.86 MW，占总用电量的8.2%、7.7%。可见，工业用户在小风季时期的需求响应潜力较大。因此，在小风季风电出力不足导致电力供需形势较紧张时，可以通过工业用户的需求响应以实现削峰、保障电网安全稳定运行的作用。

5 结论

本文通过构建工业用户需求相应潜力测算模型，计算了华北某地区工业用户在大小风季的需求响应潜力。通过K-Mediods聚类方法避免了负荷异常值的影响，提高聚类结果可靠性；通过结合负荷特性指标降维方法，有效提高了聚类效率。利用本文所提方法可更加直观地展现出工业用户的用电特性，具有可操作性和可复制性，计算结果可为工业用户用电行为特点分析及需求响应潜力的量化提供参考，为需求响应计划的实施提供理论依据。