面向地球表面三维空间的远程监视覆盖优化*
2023-03-02李奇真
李奇真
(中国西南电子技术研究所,成都 610036)
0 引 言
多传感器协同组成的传感器网络能够显著提高对环境的探测、感知能力[1]。传感器网络对热点区域、热点目标的感知覆盖是全方位有效监视、监控热点区域、热点目标的前提。传感器网络感知覆盖通常分为目标覆盖、区域覆盖和栅栏覆盖[2]。随着科技发展,入侵目标具有隐身性、高机动性等特点,其可见性具有时间、位置上的不确定性,以区域覆盖最大化为目标,部署传感器网络能够最大程度上快速发现目标。
目前对区域覆盖的研究工作主要集中在理想的二维平面,而在实际应用中,传感器节点和待监视目标都分布在三维空间中,针对传统二维感知模型和二维平面待感知区域的感知覆盖优化算法很难应用到现实复杂的三维环境中[3-4]。
三维有向传感器能够聚焦感知范围,增大感知距离,因而能够对目标空间进行远距离监视。然而,现有三维有向传感器网络感知覆盖的相关文献主要研究多媒体传感器网络,其只针对近距离待感知区域(空间),未考虑地球表面曲率对远程感知覆盖的影响。肖甫等人[5]提出了一种面向三维感知的无线多媒体传感器网络覆盖增强算法,感知模型为三维椎体,监视区域仍是二维平面。丁志强等人[6]针对复杂环境下的有向监控设备网络,建立了三维感知模型,提出了在三维空间区域中结合虚拟力及区域权重的设备监控方向调整方法,其三维空间为近距离目标空间。贾子熙等人[7]和王昌征等人[8]针对三维空间覆盖问题重新定义了三维感知模型,采用粒子群优化算法对空间覆盖率进行优化,其感知类型仍为近距离感知。Ru等人[9]给出一种无人机无线多媒体传感器网络对复杂平面的三维感知算法,该算法并未涉及对地球表面三维待感知空间的远程覆盖。Cao等人[10]采用分布式并行多目标进化算法解决智慧城市复杂环境中异构无线有向传感器网络的三维部署优化问题,与本文考虑的远程待监视空间及传感器优化参数有很大差异。
本文提出一种面向地球表面三维空间的监视覆盖优化算法:首先,将地球表面待监视三维空间进行离散化处理,并建立传感器三维有向感知模型;然后,根据传感器感知距离范围、角度范围以及地球曲率因素计算传感器网络对三维空间的感知覆盖率,采用粒子群算法和遗传算法对待监视的三维空间进行优化覆盖,分别处理连续优化变量和离散优化变量;最后,给出面向地球表面三维空间感知覆盖的仿真想定。通过实验对比了两种智能优化算法的收敛速度和覆盖率,为实际三维有向传感器部署提供了指导性意见。
1 地球表面三维空间的远程监视覆盖问题
1.1 三维有向感知模型构建
传感器三维有向感知模型由球顶椎体表示,即一个圆锥面和一个球面所围成的立体,其中圆锥面的顶点与球面的球心重合,如图1所示。三维有向传感器的感知空间可以用四元组(S,V,D,α)来表示,其中,S表示传感器所在位置,在直角坐标系中用(x,y,z)表示;V表示感知方向,可用俯仰角和方位角表示;D表示感知半径;α表示感知半顶角。
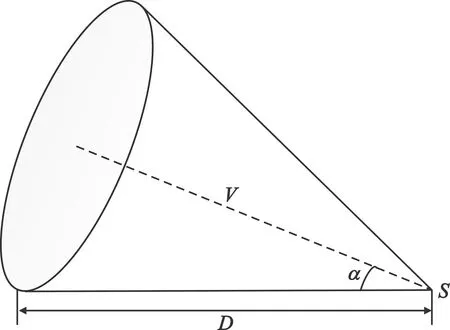
图1 三维有向感知模型
1.2 待监视空间离散化处理及可见性分析
本文考虑的待监视空间是地球表面上一定区域、一定大地高范围的三维空间,如图2红色部分所示。在实际应用中,传感器节点位置、待监视空间位置往往以大地坐标的形式给出,例如待监视空间中某点的大地坐标表示为(B,L,H),三元素分别表示纬度、经度和大地高。设该点的地心直角坐标为(X,Y,Z),根据文献[11]给出的坐标转换方法,大地坐标到地心直角坐标的转换由函数(X,Y,Z)=blh2xyz(B,L,H)完成,地心直角坐标到大地坐标的精确转换由函数(B,L,H)=xyz2blh(X,Y,Z)完成。
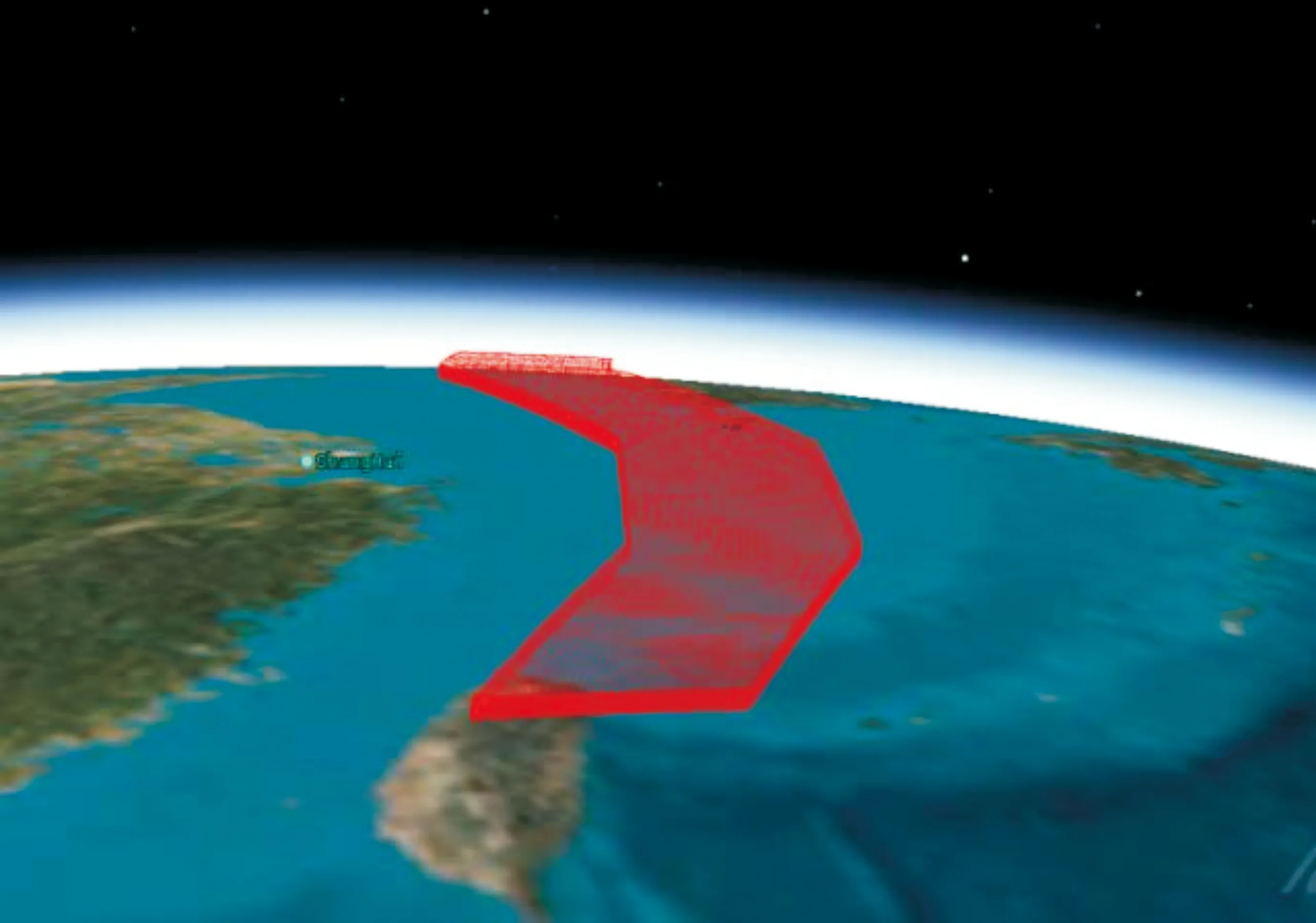
图2 地球表面待监视三维空间示意图
已知三维有向传感器的大地坐标(Bs,Ls,Hs)及其主感知方向的俯仰角γ和方位角θ,下面求主感知方向在地心直角坐标系下的方向向量。传感器地心直角坐标表示为Ps=blh2xyz(Bs,Ls,Hs),地心直角坐标系下的传感器正北方向向量可以近似表示为
VN=blh2xyz(Bs+ξ,Ls,Hs)-Ps。
式中:ξ为足够小的正实数,如0.000 1。
正东方向向量可以近似表示为
VE=blh2xyz(Bs,Ls+ξ,Hs)-Ps。
视平线方向向量可以表示为
设传感器主感知方向上的一点Cs的地心直角坐标为(x,y,z),主感知方向向量为Vs=Cs-Ps,主感知方向向量与地球切面的夹角为俯仰角γ。设传感器所在位置Ps的地心直角坐标为(xs,ys,zs),地球切平面法向量为ns=(b2xs,b2ys,a2zs),其中a和b分别表示地球椭球的长半轴和短半轴长度。利用叉乘法求解过传感器节点,地球切面法向量ns、视平线向量VAz所表示平面的法向量n=(n1,n2,n3),计算公式如下:
n=VAz×ns。
(1)
主感知向量与该法向量垂直,那么
n1(x-xs)+n2(y-ys)+n3(z-zs)=0。
(2)
主感知方向向量与视平线方向向量的内积方程表示为
Vs·VAz=cosγ|Vs||VAz|。
(3)
将主感知方向向量的L2范数|Vs|2设为任意正常数C,以如下方程表示:
(x-xs)2+(y-ys)2+(z-zs)2=C。
(4)
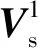
(5)
式中:符号·表示内积运算。上式判断方法表示以过传感器的地球切平面为基准平面,过与地心同侧点的方向向量为俯角向量,过与地心异侧点的方向向量为仰角向量,从而根据俯仰角的符号选择正确的解向量。通过上述算法,根据传感器主感知方向俯仰角、方位角及位置坐标,能够得到传感器主感知方向向量Vs。
待监视空间通常是不规则的立体空间,难以通过解析的方式计算传感器网络对待监视空间的覆盖情况,本文考虑以一定的颗粒度在纬度B、经度L和大地高H三个维度上对待感知空间等间隔离散化。根据传感器感知距离、感知角度、地球表面曲率约束条件,判断待监视空间中的离散点能否被传感器感知覆盖。设待监视空间某离散点的大地坐标d(Bd,Ld,Hd),根据文献[12]和文献[13],无线电极限视距广泛采用下面的经验公式:
(6)
式中:Re=4R/3为地球等效曲率半径,R=6.37×106m为地球曲率半径;Hs、Hd和DLOS的单位都为m。

1.3 远程监视覆盖率计算
与文献[5]中传感器网络监视覆盖率计算类似,首先对地球表面三维空间进行离散化处理,即在纬度、经度和大地高上分别间隔ΔB、ΔL、ΔH取离散点,从而将连续三维空间的覆盖问题转化为对目标空间中离散点的覆盖问题。设目标空间离散化后对应的离散点集合为Ω,所有至少被一个传感器覆盖的离散点集合为Ω1,则目标空间监视覆盖率定义为
(7)
式中:符号|·|表示集合中的元素数量。
本文仅考虑位置固定的传感器,优化变量是每个传感器的俯仰角和方位角,分别表示为γi和θi,其中i=1,2,…,N,N为传感器的数量。目标空间监视覆盖率是所有传感器俯仰角和方位角的函数,即CR=f(γ1,θ1,…,γN,θN)。本文的目的是通过调整每个传感器的俯仰角和方位角,最大化传感器网络对目标空间的监视覆盖率,从而得到每个传感器对应的最优主感知方向,表示如下:
(8)
2 基于智能算法的覆盖优化方法
目标空间的监视覆盖优化问题是多变量组合优化问题,覆盖率函数难以表示成自变量的闭合表达式,所以不能利用传统的凸/非凸优化方法求解每个传感器的最优主感知方向。为此,本文采用智能算法进行目标空间的监视覆盖优化:首先考虑每个传感器的俯仰角和方位角为连续变量,采用粒子群优化算法[14]求解所有传感器的最优俯仰角和方位角;其次,考虑到地球表面三维空间距大地的高度范围较小,传感器俯仰角对覆盖率的影响较小,采用遗传算法[14]求解所有传感器的最优离散化方位角,从而有效降低算法复杂度。
2.1 连续方位角/俯仰角优化
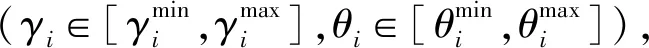
Step1 计算每个个体中每个优化参数的更新速度,公式如下:
(9)
(10)
式中:r∈(0,1)是随机数,若速度更新值超过边界,则在更新速度可取范围内随机取值作为有效速度更新值。
Step2 更新每个个体中的俯仰角γi和方位角θi,公式如下:
γi=γi+vγi,θi=θi+vθi。
(11)
若俯仰角γ和方位角θ的更新值超过参数边界,则在优化参数可取范围内随机取值作为有效参数更新值。
Step3 计算每个个体的适应度值(即传感器网络对目标三维空间的覆盖率,如公式(7)所示),与群体历史最优适应度值比较,判断本代适应度值是否优于群体历史最优适应度值,若是将本代适应度值替换群体最优适应度值,否则保留当前群体历史最优适应度值。
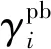
2.2 离散方位角优化
目标空间的大地高范围较小,传感器俯仰角对目标空间覆盖率影响较小,本小节将每个传感器的俯仰角固定在一个较优的值(如0°),将方位角进行离散化、二进制编码,利用遗传算法对其进行优化,从而得到最大监视覆盖率下的传感器网络最佳方位角组合。
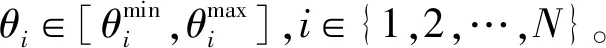
Step1 初始化参数:设置进化代数计数器g=0,设置最大进化代数G,随机生成Np个个体作为初始群体P(0),计算群体中每个个体的适应度,并对其进行排序。
Step2 选择运算:将选择算子作用于群体,根据个体适应度,按照一定规则和方法(如轮盘赌方法),选择一些优良个体遗传到下一代群体,保留当前适应度最佳个体。
Step3 交叉运算:交叉算子作用于群体,对选中的成对个体,按照某一概率交叉它们的部分染色体,产生新的个体,并保留当前适应度最佳个体。
Step4 变异运算:将变异算子作用于群体,以一定的概率改变某一或某些基因值为其他等位基因,并保留当前适应度最佳个体。
Step5 群体P(t)经选择、交叉、变异运算得到下一代群体P(t+1),计算其适应度值,并对根据适应度进行排序,准备进行下一代遗传迭代。
Step6 终止条件判断:若g≤G,则g=g+1,转到Step 2;若g>G,则进化过程中得到的最佳适应度个体作为最优解输出,算法结束。
3 仿真结果与分析
本文仿真计算机CPU为Intel Core i5-6500,主频3.2 GHz,采用Matlab软件仿真固定位置有向传感器网络对地球表面三维空间监视覆盖优化,优化算法包括粒子群优化算法和遗传优化算法,其中粒子群优化算法包括俯仰角可调整和俯仰角固定两种情况,遗传算法优化离散编码的方位角。
仿真场景如图3所示。设置固定位置三维有向传感器网络中的传感器数量为5,每个传感器的位置、感知半角和默认最大感知距离如表1所示。地球表面待监视目标空间为纬度、经度和大地高在一定取值方位的三维空间,其中,纬度取值范围为北纬26.5°~35.5°,经度取值范围为东经123°~127°,大地高取值范围默认为5 000~20 000 m。纬度和经度的离散化颗粒度为0.1°,大地高的离散化颗粒度为100 m。
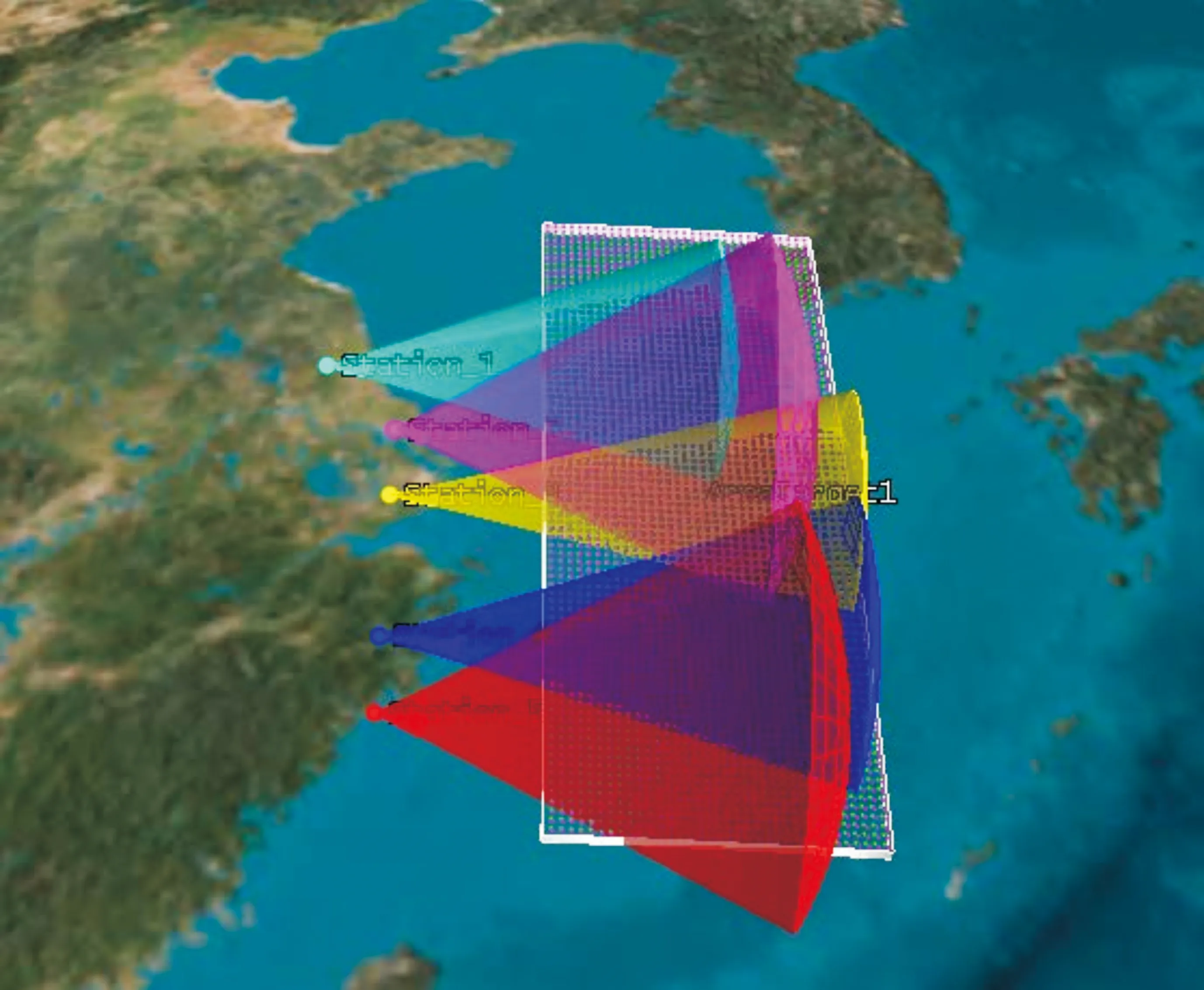
图3 仿真场景设置
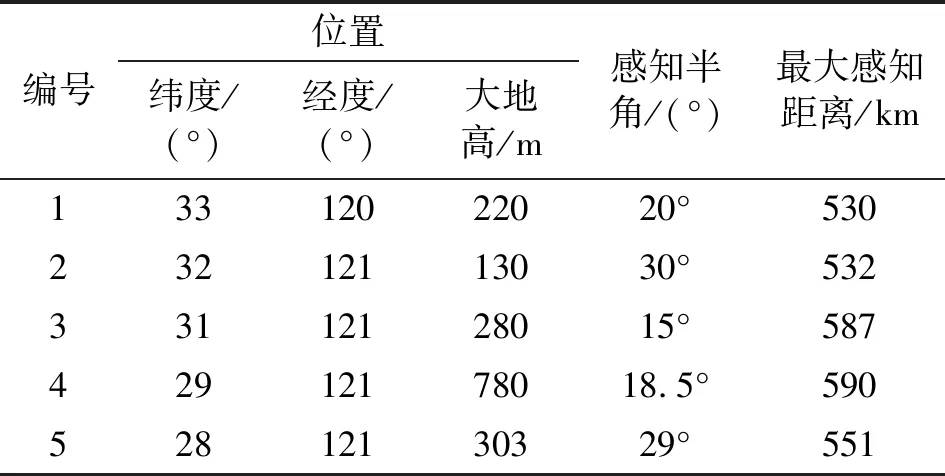
编号位置纬度/(°)经度/(°)大地高/m感知半角/(°)最大感知距离/km13312022020°53023212113030°53233112128015°58742912178018.5°59052812130329°551
对于三种优化算法,群体中的个体数量均为50,进化代数为100。针对粒子群算法,设定俯仰角边界为[-3°,3°],方位角边界为[60°,120°],俯仰角更新速度边界为[-1°,1°],方位角更新速度边界为[-5°,5°],惯性权重w=0.8,自学习因子c1=0.5,群体学习因子c2=0.5。针对遗传算法,每个传感器的方位角边界为[60°,120°],由8位二进制数编码,染色体从高位到低位的交叉起始点随机选择,交叉概率为0.25,变异概率为0.01。
三种算法的群体历史最优适应度随迭代次数的变化曲线如图4所示,每条曲线是5次仿真的平均值,其中,蓝色实线表示俯仰角可调整粒子群算法结果,红色点线表示俯仰角固定粒子群算法结果,黑色点划线表示遗传算法结果。由仿真结果可知,俯仰角固定粒子群算法最终收敛结果与俯仰角可调粒子群优化算法相当,两种粒子群算法均优于遗传算法,这说明俯仰角优化对收敛结果影响较小,自变量离散化编码对收敛结果影响较大。
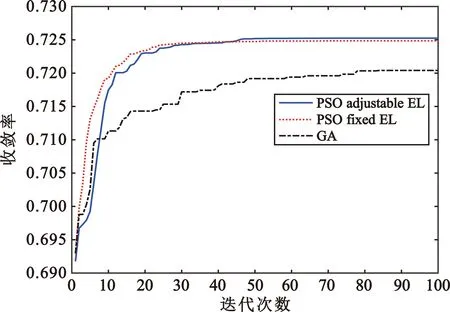
图4 群体历史最优适应度变化曲线
以固定俯仰角粒子群算法为例仿真了传感器最大感知距离对覆盖率的影响,结果如图5所示,其中,蓝色实线表示默认最大感知距离下的结果,红色点线表示所有传感器最大感知距离增大10 km的结果,黑色点划线表示所有传感器最大感知距离减小10 km的结果。由仿真结果可知,随着传感器感知距离增大,传感器网络覆盖率同时增大,其增长速度变缓。这一方面因为一些传感器感知范围超出待监视空间,另一方面大地高程较小、距传感器较远的目标空间离散点被地球遮挡,未被传感器覆盖,新增被覆盖离散点与新增待监视空间离散点的比值减小。
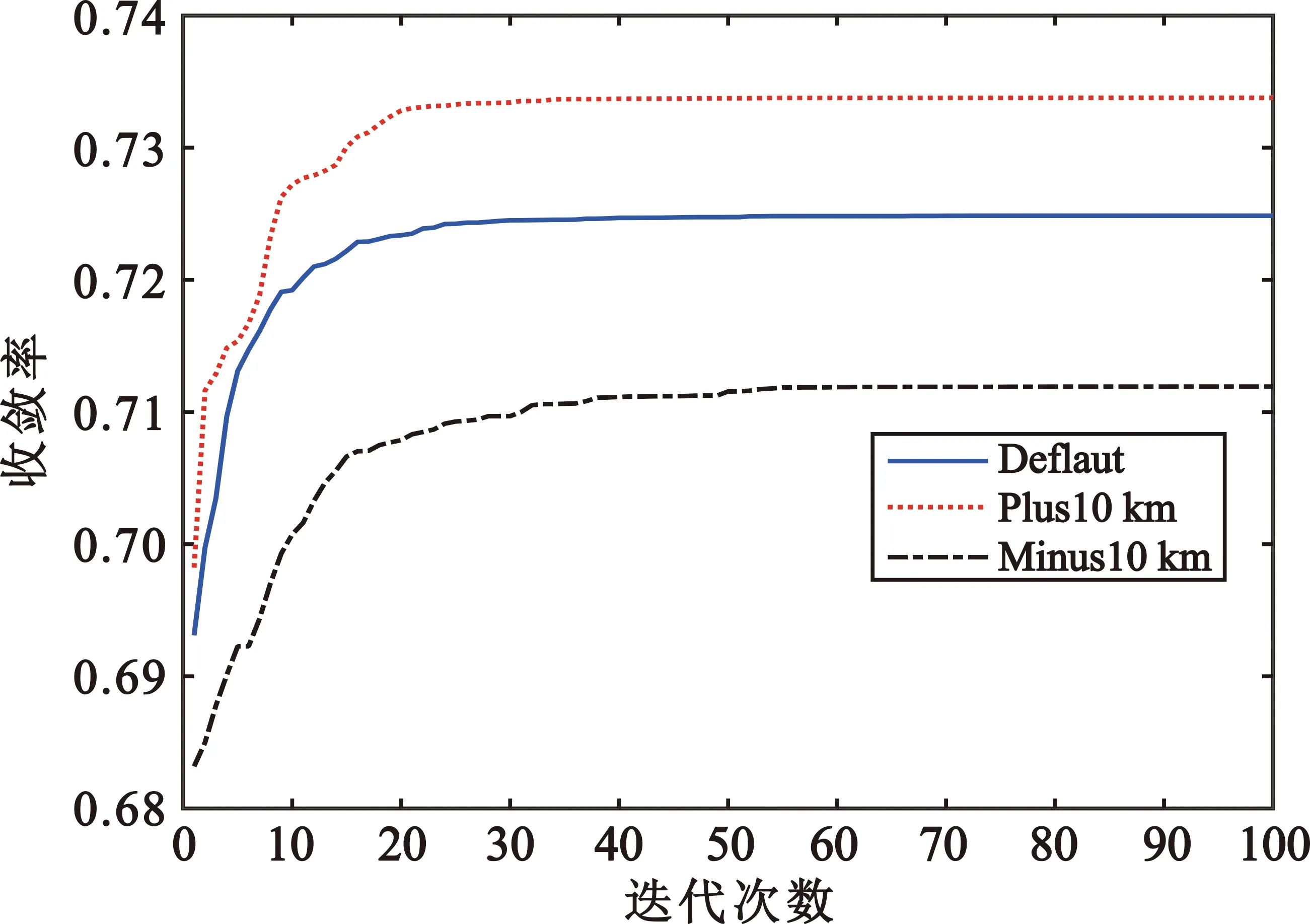
图5 传感器最大感知距离对覆盖率的影响
以固定俯仰角粒子群算法为例仿真了不同大地高范围目标感知空间的覆盖率,结果如图6所示,其中,蓝色实线为默认大地高范围结果,红色点线为大地高范围4 000~19 000 m的结果,黑色点划线为大地高范围6 000~21 000 m的结果。由仿真结果可知,随着大地高程增大,传感器网络对目标空间的覆盖率也增大,原因是根据公式(6),大地高较小的目标空间离散点被地球遮挡,传感器网络对该部分离散点无法有效覆盖。
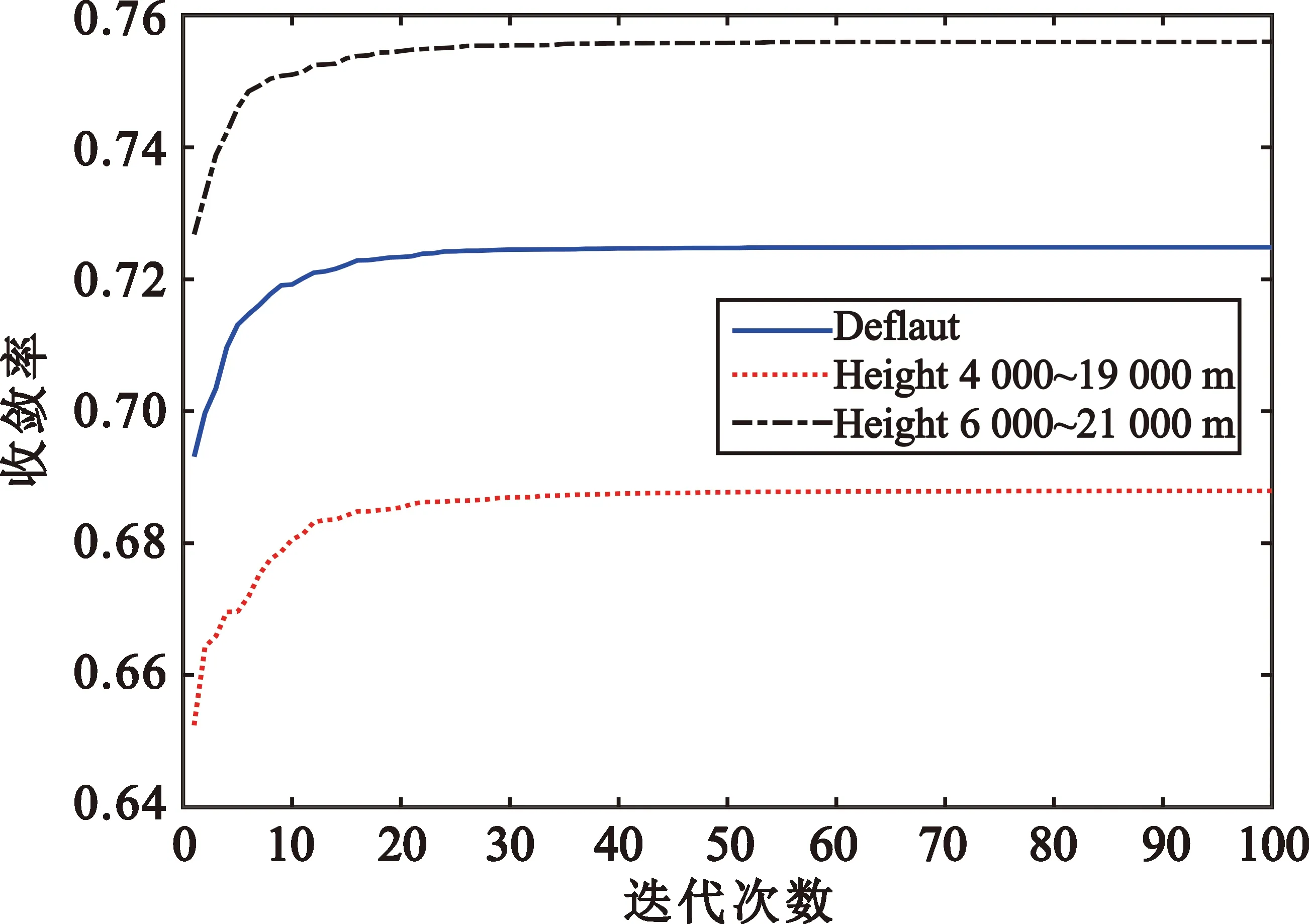
图6 目标空间大地高范围对覆盖率的影响
仿真过程中发现,俯仰角可调粒子群算法需要求解方程组,其时间复杂度(每轮迭代平均用时1 760 s)远高于其他两种算法(俯仰角固定粒子群算法平均用时35.98 s,遗传算法平均用时34.90 s),因此,在地球表面空间大地高范围较小的情况下,建议使用固定俯仰角粒子群优化算法。
4 结束语
本文建立了地球表面曲率影响下的三维目标空间模型以及传感器三维感知模型,提出了基于粒子群算法和遗传算法的面向地球表面三维空间的远程监视覆盖优化算法,通过仿真分析了不同参数下两种算法的性能及效率,为有向远程感知传感器网络的部署提供了技术支撑。
本文提出的智能优化算法适应度为目标空间的一重覆盖率,然而一重覆盖下传感器网络不能对目标空间进行协同监视,且可能在入侵方向上存在入侵盲区。在后续工作中,将进一步采用多目标适应度函数,加入空间多重覆盖和入侵方向栅栏覆盖作为优化目标,提高目标空间监视效果。此外,本文对目标空间离散化处理,分别对每个传感器到每个离散点进行可见性分析,串行计算非常耗时。后续工作中,将研究并行计算方法,以降低算法的时间复杂度。
