基于三元采样图卷积网络的半监督遥感图像检索

冯孝鑫 王子健 吴 奇*

①(上海交通大学电子信息与电气工程学院 上海 200240)

②(香港大学化学系 香港 999077)

1 引言

近年来由于遥感卫星数量的增多，导致遥感图像的数据量正在以指数级增长，这对遥感数据库的设计提出了新的挑战。图像检索是遥感数据库的基本功能，如何在遥感图像数据库中准确地对给定查询图像的相关图进行检索是当下遥感图像数据库一个重要的研究内容。基于内容的图像检索(Content-Based Image Retrieval, CBIR)正在成为具有海量图像的大型遥感数据库值得深入探索的技术问题。

为了实现准确的CBIR，国内外相关研究提出了多种基于深度学习的图像检索方法，特别是基于卷积神经网络(Convolutional Neural Networks,CNN)的图像检索方法以其强大特征提取能力受到了广泛的关注[1]。例如，Ye等人[2]提出了一个两阶段模型，首先通过CNN提取图像特征，再根据特征空间中的加权距离计算图像的相似度来评估数据库图像与给定查询图像的相似性。为了实现可扩展和高精度的图像检索，Roy等人[3]提出了一种基于度量学习的深度哈希网络以学习遥感图像的哈希码。该网络将图像的三元组作为输入，驱动度量学习并得到嵌入空间。目前，将三元组与三元组损失函数[4]结合使用是训练深度度量学习模型的常用方法。三元组即由一个锚点样本、一个与锚点样本同类别的正样本以及一个来自其余类别的负样本组成的一组训练样本。由三元组损失驱动的深度模型旨在减小同类图像样本在度量空间中的距离并增大不同类图像的距离。学习得到的嵌入空间的有效性在一定程度上取决于所选择的三元组。因此，选择合适的三元组有助于提高度量学习模型最终的图像检索性能。

目前一些研究表明[5]，基于度量空间(空间中语义相似的图像彼此接近)的深度度量学习方法在遥感图像检索任务中具有显著效果，尤其是基于三元组的度量学习方法。其优化目标是在最小化锚点与其正样本之间的特征距离的同时最大化锚点与负样本之间的特征距离，最终使得正样本比负样本更接近锚点样本。如果三元组中的锚点样本与正样本之间的距离小于锚点样本与负样本之间的距离，则该三元组被视为困难三元组(Hard Triplet)。反之，如果三元组中的锚点样本与正样本之间的距离大于锚点样本与负样本之间的距离，则该三元组被视为简单三元组(Easy Triplet)。图1展示了三元组的度量学习和度量空间更新过程。其中，图像Xp和Xn分别作为正样本和负样本图像，与锚点图像Xa共同构成困难三元组。图像样本之间的距离表征了图像样本之间的相似度。在三元组损失的驱动下，该三元组更新度量空间后，Xp被拉近Xa得到Xp′，而Xn则 被疏远Xa得到Xn′。

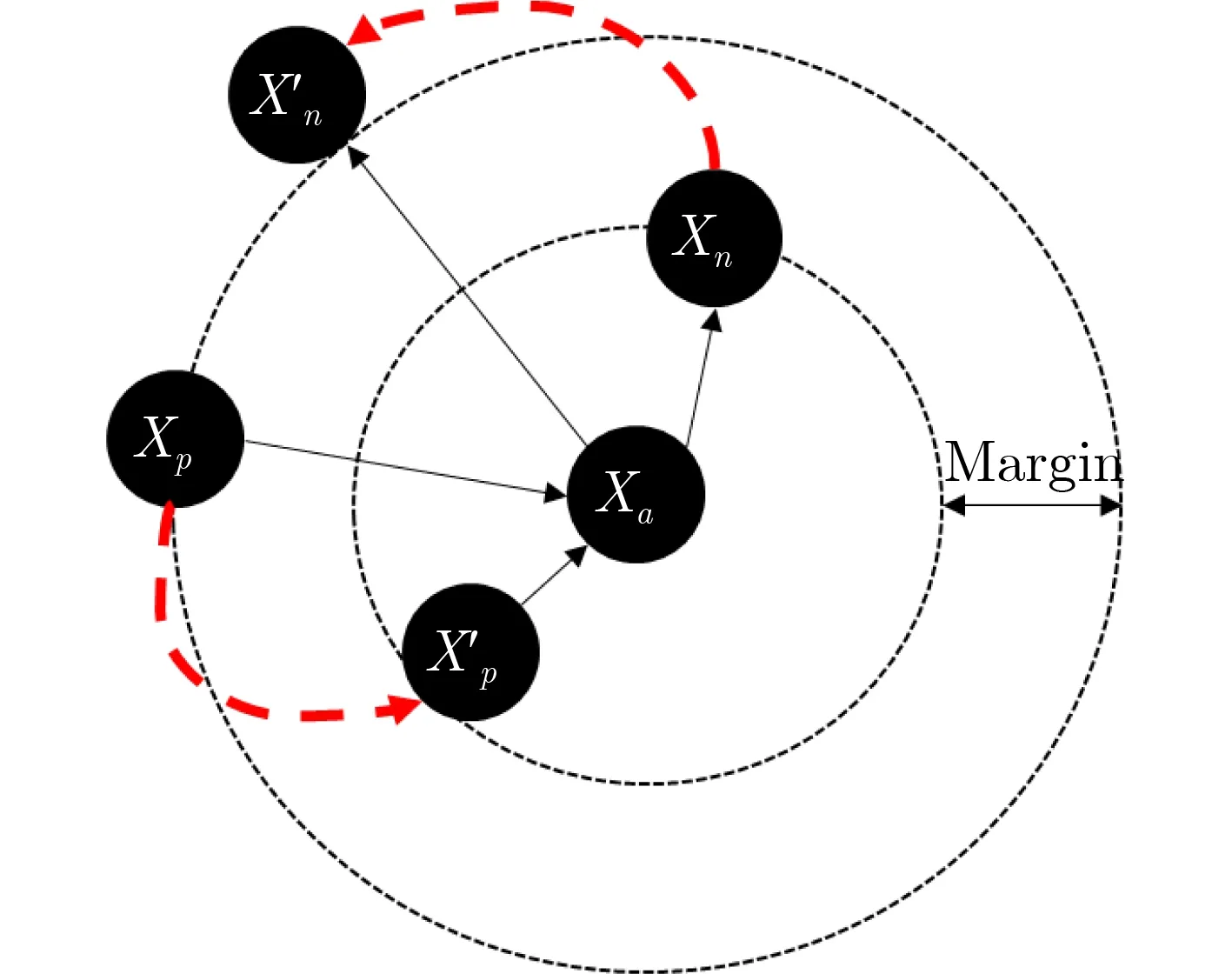
图1 三元组与度量学习

随机三元组采样算法(R a n d o m T r i p l e t Sampling, RTS)指在训练样本中采用随机选择的方式根据样本类别标签构建三元组的方法，由于数据的类内相似性和类间相似性差异，通过此种方法构建的三元组有很大比例为简单三元组。在训练中，如果使用简单三元组组成的样本集合，将导致计算损失时梯度值小，收敛速度慢。因此，选择利用构建困难三元组组成的样本集合进行训练能够获得更高损失值与梯度值，从而有效地加速模型参数的更新。

三元组深度度量学习算法的研究主要包含三元组损失函数改进和三元组采样算法优化两个方面。针对三元组损失函数的研究中，Zhang等人[6]基于focal loss对现有的三元组损失函数进行了改进，赋予困难三元组更高的权重。Kim等人[7]提出了新的用于姿态估计的三元组损失，其保留了嵌入空间中与标签空间的距离比。部分研究同样聚焦于提出具有加权策略的三元组[8,9]，增强困难样本在训练中的效果。Wang等人[9]提出了多类别N对损失函数的三元组损失函数。Zhang等人[10]引入了Dual-anchor三元组损失函数，除了三元组损失的目标之外，该损失函数同时增加了给定锚点与正样本和负样本之间的距离。Wu等人[11]证明当使用相同的采样算法时，使用不同改进损失函数的深度学习模型能够得到相似的精度水平。

目前遥感图像领域的大多数方法在选择三元组中样本图像中并未考虑到所选择三元组中样本图像的性质，主要利用上文中提到的随机三元组采样算法[11]。而在计算机视觉领域的研究中，三元组选择的重要性则被更广泛的研究[12]。例如，Xuan等人[13]提出了一种三元组选择算法，为每个锚点样本选择最接近的简单正样本(Easy positive)和最接近的困难负样本(Hard negative)。Yuan等人[14]提出HDC (Hard-aware Deeply Cascaded)嵌入方法。对于每个锚点和一个选定的正样本，HDC选择多个难度级别的负样本来构建不同的三元组。其中，难度级别根据嵌入空间中的距离定义。上述两种算法无法有效学习正类中的难样本。而Yang等人[15]则通过将正样本图像与该批次中的所有负类图像对组合对困难正样本进行了研究。Ge等人[16]同样提出了一种困难三元组选择方法，该方法为整个数据集构建图像特征的类级层次树，并递归合并视觉上相似的类，基于锚点图像和不同图像类对之间通过分层树计算的距离来选择三元组。然而，这类算法往往需要在整个数据集或大批量样本中采样困难三元组，效率较低且网络泛化性差，易陷入局部最优。可以发现，现有主流三元组算法在困难三元组采样上仍存在不足，因此，本文聚焦于提出一种更合理有效的困难三元组采样算法。

目前，大多数基于三元组的方法根据图像类别选择样本从而构建三元组。然而，此类有监督的学习方式意味着需要大量有标注图像[17]。在实际的遥感图像应用中，获取大量的有标注遥感图像是一件耗时、耗力、标注难度极大的工作。近期的部分研究已经证明，通过基于图结构的半监督方式学习图像表征以及学习不同图像之间的关系有着显著效果[18]。基于图结构的半监督学习的主要思想是通过将训练图像的标签借助图结构(其中节点表示图像，边描述图像之间的关系)传播到未标注的图像节点上。近年来已出现一系列通过深度神经网络来提取和利用图结构特征的方法，其中，图卷积网络(Graph Convolutional Network, GCN)是最具代表性的一种方法。图卷积网络是由Duvenaud等人[19]提出的，GCN被定义为在图结构化数据上实现端到端学习的一种卷积神经网络。之后，Jiang等人提出Graph Learning Convolutional Network，以获得用于半监督学习的最佳图表示。Bruna等人[20]使用平滑谱乘子在图上构建了Spectral-based深度神经网络。此外，Kipf等人[21]首次采用GCN进行半监督分类。

在遥感领域，Kang等人[22]提出一种基于图网络的多标签遥感图像分类与检索方法，通过图结构对多标签遥感图像的标签依赖性和场景相关性进行建模。Chaudhuri等人[23]基于学习遥感图像的判别特征空间提出了Siamese GCN模型，以实现图像检索。该模型由两个GCN组成，用于测量一对图嵌入样本之间的相似性。孪生GCN架构实现了相应样本度量空间的学习。然而，由于仅考虑样本对，孪生GCN架构难以充分捕获具有复杂语义内容的遥感图像存在的高阶相关性。计算机视觉领域近期提出了一种度量学习算法框架，其使用一种三元组驱动的有监督度量学习框架来学习图之间的距离[24]，通过比较图编辑距离(Graph Edit Distance, GED)的近似值，将三元组损失直接应用于图样本之间。上述几种代表性算法均为有监督算法，由于需要大量有标注的图像，限制了其在遥感图像检索领域的适用性。可以发现，基于度量学习的主流算法在遥感半监督场景下普遍存在局限性，无法有效学习无标注数据。因此，本文聚焦于提出一种基于图卷积网络的半监督三元组算法，并应用于遥感图像检索。

综上可以看出，遥感领域以三元组算法为代表的度量学习方法主要存在两方面的局限性，一是困难三元组采样有效性不足，二是三元组算法无法用于半监督学习。为解决以上问题，准确表征遥感图像内容以及评估不同图像之间的相似性关系，本文提出了一种新的用于半监督遥感图像检索的三元采样图卷积网络。提出的方法在两个遥感数据集上开展了实验验证。实验结果说明了提出方法的可行性。此外，通过与基于三元组的近期深度度量学习方法相比，所提出的方法在准确学习度量空间方面的优越性得到了验证。

基于以上考虑，本文提出的遥感图像检索方法的主要创新点如下：

(1) 考虑到遥感图像检索的复杂性，提出了基于三元图卷积网络(Triplet Graph Convolutional Network, TGCN)的度量学习方法，以刻画遥感图像具有的复杂语义以及不同图像之间存在相似性关系；

(2) 考虑到三元组采样方式对度量学习效果的影响，提出了基于图的三元组采样(Graph-based Triplet Sampling, GTS)算法，通过图结构选择最有效的三元组，从而提升度量学习模型训练效率和精度；

(3) 考虑到遥感应用中标注样本稀缺的问题，提出了半监督三元组算法，通过对图的无标注节点分配伪标签，并进一步用于构建三元组辅助训练，从而提升算法半监督场景下的性能。

本文的结构如下：第2节介绍三元采样图卷积网络的结构和算法原理；第3节给出实验设计、实验结果及分析，并在两个遥感数据集上进行实验。通过与当前主要度量学习算法的对比，在半监督场景下验证了所提出算法的优越性；第4节对本文进行了总结。

2 三元采样图卷积网络

2.1 三元图卷积网络

本文所提出的基于三元采样图卷积网络由具有基于图的三元组采样GTS算法的TGCN组成。其中，TGCN包含3个结构相同的网络，彼此共享参数并以端到端的方式进行训练(见图2)。每个网络由一个基于ResNet的CNN和一个3层GCN组成。给定一批训练图像X={xt}t=1,...,T，CNN作为嵌入网络，通过嵌入函数φ(·)获 得每个图像xt ∈X的特征嵌入φ(xt)。具体来说，将一组由输入图像中锚点、正类和负类图像(根据标签相似性随机选择)构成的三元组分别输入各自对应的CNN网络φa，φ+和φ−中，输出得到三元组对应的特征嵌入，将该特征嵌入分别用于构建图Ga，G+和G−的初始节点。各图其余节点使用来自X的剩余训练图像(包括标注和未标注图像)构建。

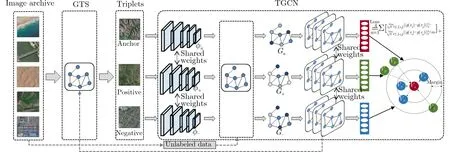
图2 三元采样图卷积网络

图3给出了图结构的详细构建方式，图结构Ga=(Va,Ea)以 锚点和来自X的其余图像作为初始节点进行构建。其中，vi ∈V代表第i个节点，eij=(vi,vj)∈E代表一个连接vi和vj的 边。图Ga的第i个 节点vi ∈V初始状态为图像嵌入特征ϕ(xi)和图像标签li的o n e-h o t 编码hi的拼接向量，即vi=(ϕ(xi),hi)。

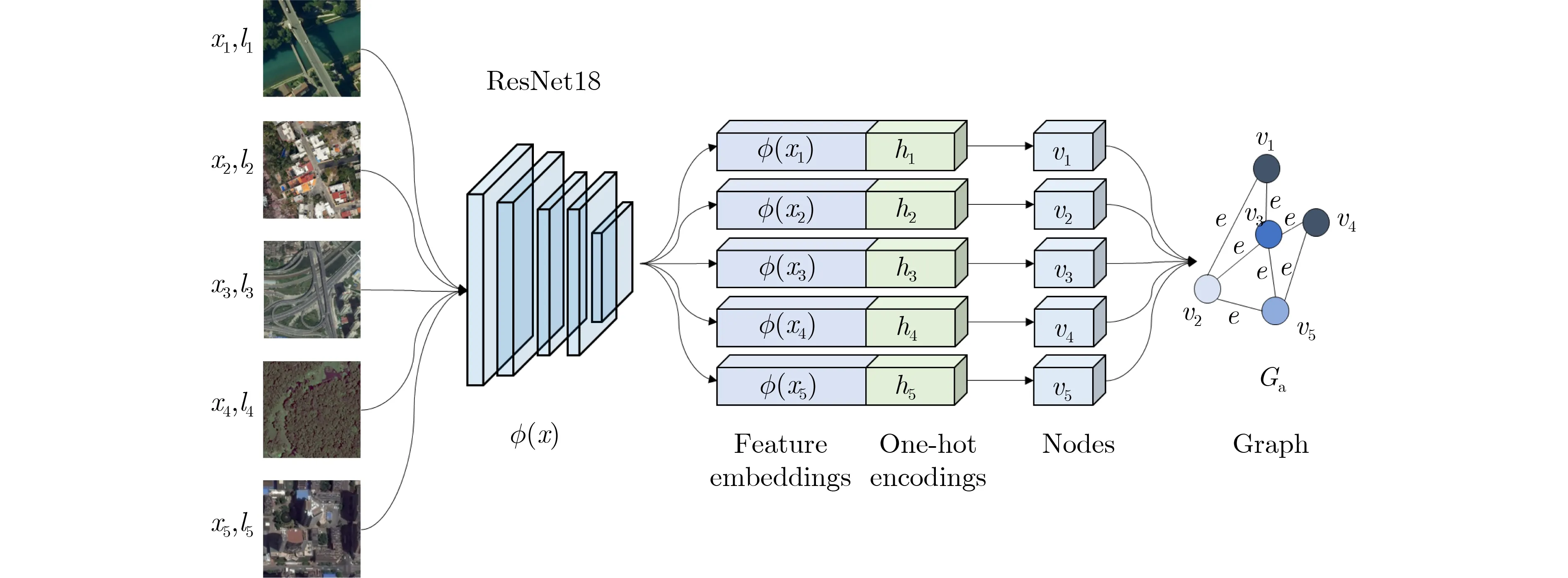
图3 图构建方式

图的节点属性用节点特征矩阵Z ∈Rn×d表示，其中zv ∈Rd是节点v的特征向量。

A ∈Rn×n是邻接矩阵，其中Aij表示vi和vj的连通性。基于邻接关系，标签信息通过图结构从标注图像传播到未标注图像。

其中，Θ∈Rd×l表示网络第k个卷积层中的可学习参数，ρ表示leaky-ReLU激活函数。

在每个GCN层之前，通过由3层神经网络Fθ参数化的对称函数ψθ从节点的当前隐藏状态中学习得到邻接矩阵A。两个节点的相似度根据节点的特征距离得到，表示为

与图Ga类 似，用同样的方式构建图G+和G−并将其分别作为正类图样本和负类图样本。之后将构建的图输入到GCN中，GCN通过图卷积操作对图特征进行学习，并对标签进行传播，输出得到图嵌入。

最终，构建的TGCN通过三元组损失进行优化，该损失函数由GCN提供的图嵌入作为三元组样本输入。

2.2 基于图卷积的三元组采样

为了训练基于三元组的深度度量学习模型，选择信息丰富且有效的三元组至关重要。选择三元组的常用方法是基于类标签相似性对图像进行随机选择，即在与锚点相同的类中随机选择正类图像，并在任何其他类别中随机选择负类图像。这种随机三元组采样算法可能会获得许多简单三元组。由于简单三元组在训练过程中不会引起网络参数的显著变化而导致训练效果较差[5]。为了避免该问题，本小节提出GTS算法，通过TGCN中训练的图卷积网络在图结构中度量不同节点之间的相似关系，从而针对锚点图像节点在图上其余节点中选择对应的困难正样本与困难负样本节点。通过该方式构建困难三元组，能够使模型准确地学习不同类别之间的本质差异[4]。具体的采样算法如下：

通过以上方式，困难正样本图像可被自动选择用于构建三元组。困难负样本图像的选择可以通过相同的方式来实现。困难三元组的损失函数计算为

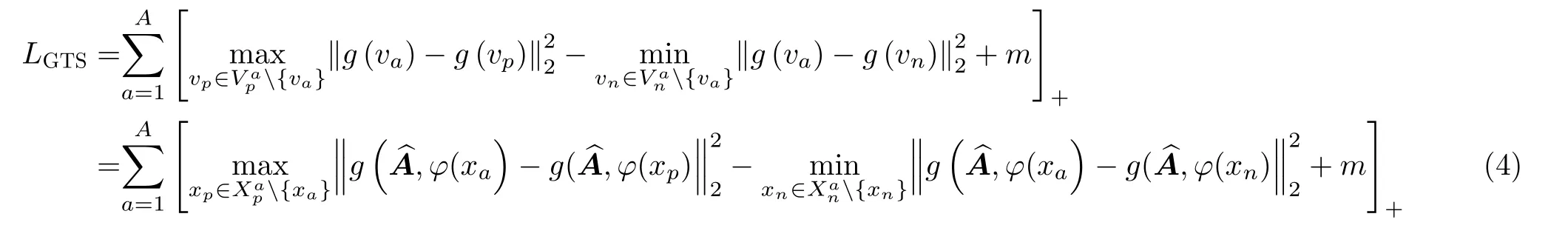
此外，本文的图像检索是通过在由TGCN构建的图嵌入空间中使用的k-最近邻算法实现的，即获取查询图像并计算查询图像与所有存档图像之间的相似度函数以找到与查询最相似的k个图像。

2.3 半监督三元组

基于三元组损失的度量学习是一种需要依赖于样本标签信息的有监督学习。其通过样本标签划分正样本和负样本，因此无法有效地利用大量的无标注训练样本。为此，本节在模型中引入基于图卷积的半监督三元组算法，通过GCN对Graph中由无标注训练样本构成的节点分配正类或负类的伪标签，将该样本也用于组建三元组Graph并用于GCN度量学习。伪标签准确度也会随训练迭代次数增加而提高，最终通过利用大量的无标注训练样本以进一步提升检索的准确性。具体的策略如下：

对于每个batch中的锚点图像xa，选择部分正 类 图 像Xp={xp}p=1,2,...,k， 负 类 图 像Xn={xn}n=1,2,...,k以 及无标注图像Xunlabel={xu}u=1,2,...,k组建mini-batch，通过CNN嵌入网络生成初始节点特征并构建图Gu输入GCN中，根据输出的图节点特征与边特征计算对应无标注图像的伪标签lu。lu的公式为

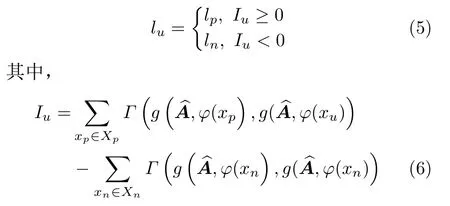
3 实验

3.1 实验设置

实验在两个不同的遥感数据集上进行。第1个数据集是Aerial Image Dataset (AID)[25]，由10000张图像组成，包含30个类别。第2个数据集是NWPU-RESISC45[26]，该数据集包含31500张图像的大型遥感数据集，共包含45个类别。对于这两个数据集，随机选择每类图像的70%和10%分别构建训练集和查询集，其余图像用于构建测试集。本文中图像检索与分类任务均基于模型学习的特征进行。验证集图像输入训练完成的模型以构建存档特征库，测试集图像输入训练完成的模型以输出图像检索的查询图像特征或图像分类的测试样本特征。本文中存档特征与测试样本特征维度均为64 维。

实验中，对于训练集，标注图像比例分为设置为5%，15%和20%3种，其余图像则被视为未标注的训练图像。用于构建图的初始节点特征是通过在ImageNet上预训练的ResNet18模型[27]获得的。来自上述两个数据集的输入图像被统一调整为256像素×256像素。训练中使用了RandomGrayscale,ColorJitter和RandomHorizontalFlip3种数据增强算法。训练的Batchsize设置为16，三元组损失的阈值m设置为0.2。随机梯度下降(Stochastic Gradient Descent, SGD)优化器被用于更新梯度。此外，初始学习率设置为0.001，每30个epoch衰减0.5倍。在实验中，使用欧几里得距离作为K-最近邻算法的相似度度量指标。实验在由2个NVIDIA Tesla P100 GPU组成的集群上进行。

为了评估所提出的基于RTS(表示为TGCNRTS)和GTS(表示为TGCN-GTS)的TGCN模型的有效性，提出的算法与以下4种度量学习和半监督学习算法进行比较：(1)基于三元组损失和Batch All Triplet Mining (BATM)的深度度量学习方法(DML)[27]；(2)D-CNN[28]；(3)SNCA[29]；(4)HRS2DML[30]。

实验的检索结果是针对不同的标注训练数据率(Labeled Training Data Rates, LTDR)呈现的，例如10%LTDR表示使用了总图像数量的10%作为有标注的训练图像。我们使用对前40幅检索得到图像的平均精度(mean Average Precision, mAP)作为检索效果的评价指标。图4展示了DML与提出的TGCN-RTS和TGCN-GTS3种算法在AID数据集上的检索图像示例。实例中查询图像为airport类，分别展示了从数据库中检索到的第1, 5, 9, 13和17幅图像。

3.2 实验结果

从图4(b)可以看出，DML错误地检索到了部分与查询图像无关的图像(第13和第17张分别属于commercial和railwaystation类)。与之相比，本文提出的TGCN-RTS和TGCN-GTS方法检索到了语义上更相似的图像。图4(c)展示了TGCN-RTS的检索结果，只有第17个检索到的图像与查询图像属于不同的类别。而在图4(d)中，TGCN-GTS检索到的所有图像都来自与查询图像相同的类别。由此验证了，相比于RTS, GTS对TGCN模型的训练能够起到更好的提升效果。

图4 图像检索结果对比

表1展示了各算法在AID和NWPU-RESISC45两个数据集上获得的检索前40幅图像的mAP。所有结果都表明TGCN在半监督场景下明显优于DML,D-CNN, SNCA为代表的度量学习算法。以AID数据集上的实验结果为例，当LTDR分别为5%，10%和20%时，TGCN-RTS算法与DML算法相比检索mAP分别提高了9.76%, 8.37% 和 1.69%(见表1)。该实验结果显著地表明通过图卷积网络能够学习到更好的数据结构性信息以及能够有效地利用未标注图像，验证了本文提出算法性能的优越性。

从表1还可以看出，TGCN-GTS在所有LTDR上的表现都明显优于TGCN-RTS，例如，在AID数据集上，对于5%, 10%和20%的LTDR，分别为14.00%, 10.03%和8.78%。表1在NWPU-RESISC45数据集上也取得了类似的效果。TGCN-RTS和TGCN-GTS之间的差异表明了三元组采样算法对最终检索准确度的重要性，相比于随机采样三元组，选择困难三元组能够显著地提高度量学习模型最终的图像检索性能。通过横向对比3种不同标注比例下的实验结果可以发现，TGCN-GTS算法在标注比例较低的半监督场景下性能提升更为显著。DML能够利用三元组损失有效学习高判别性的度量空间，然而，由于其无法有效利用无标注训练数据，在半监督场景下存在局限性。而HRS2DML为代表的半监督算法则无法有效建模细粒度遥感场景图像的类内差异性和类间相似性，训练数据标注比例越低则其学习各场景类别特征相关性的效果下降越多。与之相比，本文的TGCN-GTS算法一方面能够根据图结构的节点相关性对无标注数据分配伪标签，另一方面能够利用困难三元组学习细粒度遥感数据集的难样本，利用有限的数据学习高判别性的度量空间。因此，在标注比例较低的半监督场景中TGCN-GTS的优势更明显。

需要指出的是，提出的TGCN模型实现的图像检索准确率的提升是以训练阶段的计算复杂度略有增加为代价的。表2对比了TGCN-RTS, TGCNGTS和DML3种模型的网络参数量(Number of Parameters, NP)和浮点运算次数(Floating-point Operations, FLOPS)。通过分析表格，可以发现TGCN的NP和FLOPS与DML的比较接近。NP的增加是因为GCN引入了相关网络参数。而FLOPS增加的主要包括以下2个原因：(1)与DML相比，GCN包含更多可学习的参数；(2)GTS算法涉及选择困难三元组需要额外的计算量。值得注意的是，FLOPS与训练的离线过程相关，因此不会影响检索过程所需的在线计算时间。

表2 算法模型复杂度比较

为了进一步分析提出的GTS算法的性能，图5给出通过t分布随机邻域嵌入(t-Distributed Stochastic Neighbor Embedding, t-SNE)将选择的三元组从度量空间投影到2维空间中的结果。通过分析该图可以发现，与RTS选择的图像样本相比，GTS采样的triplet样本分布有以下特征：(1)正样本和负样本分布互相接近，视觉上互相重叠；(2)正样本和负样本呈现紧凑的聚类分布，主要由于以下2个原因。一方面GTS算法根据图结构中的相似性信息选择困难三元组，从而在度量空间中锚点与正样本距离较远而与负样本较近，此类困难正样本和困难负样本相互之间具有较难区分的高相似性。因此，在特征空间的2维映射下呈现相互重叠的位置关系。另一方面，对于每一个锚点样本，选择的困难正样本和困难负样本均属于难样本，而对于每一类锚点，其所有对应的困难负样本图像均具有与该类别图像相似度较高的特征，从而在特征空间中呈现聚类分布。因此，GTS算法相比于RTS有着更好的特征区分能力。

图5 triplet样本t-SNE 2维映射图

4 结束语

本文提出了一种针对半监督遥感图像检索问题的三元采样图卷积网络，其由三元图卷积网络TGCN以及基于图的三元组采样GTS算法组成。TGCN提供了对遥感图像复杂语义内容及其相似性的更完整和详细的表征。GTS提供了基于图的更优的样本采样方式以提升提高度量学习模型训练效率和性能。在两个遥感数据集上得到的测试结果表明，提出的TGCN-GTS由于其高精度的度量学习能力，显著地提高图像检索的准确性。鉴于三元采样图卷积网络在表征遥感图像复杂语义信息及学习具有更高特征区分度的度量空间上的潜在优越性，未来应进一步探索其在多标签遥感图像检索或分类领域内的应用。