基于均匀圆阵的近场源定位技术研究进展

刘 振 陈 鑫 苏晓龙 户盼鹤 刘天鹏 彭 勃 刘永祥

①(国防科技大学电子科学学院 长沙 410073)

②(航天飞行器生存技术与效能评估实验室 北京 100094)

1 引言

阵列信号处理[1]在通信[2]、声呐[3]和雷达[4]等领域的电子侦察环节中发挥着非常重要的作用。空间中的辐射源按照与接收阵列距离分为远场源和近场源[5,6]。通常来说，远场源与阵列间的距离大于2D2/λ， 其中D是 阵列的孔径，λ是信号的波长，此时信号近似为平面波，对远场源定位只需要对波达方向(Direction Of Arrival, DOA)进行估计[7]；而近场源与阵列间的距离小于 2D2/λ[8]，处于阵列的菲涅耳区，对近场源定位除了需要对DOA进行估计，还需要对距离参数进行估计。相对于窄带辐射源信号，宽带辐射源信号更有利于目标检测、参量估计和目标特征提取，在实际中获得了更广泛的应用。在阵列结构上，由于均匀线阵导向矩阵具有范德蒙(Vandermonde)形式，便于在数学上处理，因此研究相对广泛，但是均匀线阵的分辨力主要集中在法线方向，当DOA为±60°时，分辨力下降了1/2。均匀圆阵(Uniform Circular Array, UCA)下近场源定位场景示意图如图1所示，均匀圆阵由M个阵元组成，半径为R，第k个近场源位置为(ϕk,θk,rk)， 方位角ϕk ∈[0,2π]是从x轴按逆时针方向旋转的角度，俯仰角θk ∈[0,π/2]是从z轴按顺时针旋转的角度，rk是近场源到均匀圆阵中心的距离，rm,k是第k个近场源到第m个阵元的距离。相较于均匀线阵只能对1维DOA进行估计，均匀圆阵可以实现方位角和俯仰角等2维DOA估计[9,10]，并且在不同方位角的分辨率具有各向同性[11,12]。由于均匀圆阵的导向矩阵不具有Vandermonde形式，不能直接将均匀线阵下的方法应用在均匀圆阵。此外，当圆阵直径大于半波长时，利用相位进行参数估计会出现模糊，导致算法失效。

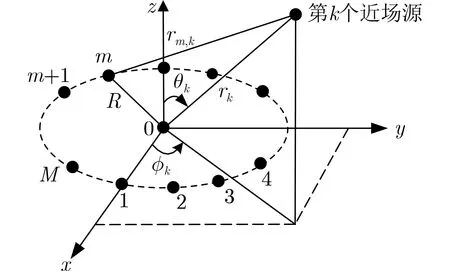
图1 均匀圆阵下近场源定位场景示意图

在近场定位的信号形式上，目前主要针对单频信号或窄带信号进行研究。相较于窄带信号，宽带信号具有目标回波携带信息量大，混响背景相关性弱，更有利于目标检测、参量估计和目标特征提取等特点[13–19]。线性调频(Linear Frequency Modulated,LFM)信号是一种典型的宽带信号，具备较强的抗多径效应、抗频谱弥散和抗干扰等特性[20,21]，逐渐应用在雷达[22–24]与声呐[25,26]中。由于基于窄带平稳信号模型提出的方法不能够表述LFM信号的时频特性，因此不能够适用于LFM信号的定位。当前LFM信号定位方法主要围绕其时频特性，提出了以基于短时傅里叶变换(Short Time Fourier Transform,STFT)[27–30]和基于分数阶傅里叶变换(FRactional Fourier Transform, FRFT)[31–33]的定位算法；当前针对宽带近场源定位主要存在以下两大挑战：一是将宽带远场源的定位方法直接运用到近场源定位中会降低定位精度，二是针对宽带信源定位的算法存在计算量大、实时性差等缺点。

为深入介绍均匀圆阵下宽带近场源定位的研究方法和进展，本文第2节首先从2阶矩、高阶累积量和相位差等方面梳理了均匀圆阵下的近场源定位方法，接着从旋转短基线和多子阵结果聚类等方面梳理了近场源定位解模糊方法，最后从时域、频域、分数阶傅里叶域等方面系统阐述了近场LFM信号的方位角、俯仰角和距离等3维位置参数快速精确估计方法。第3节对相干辐射源和近远场混合源参数估计等后续研究内容提出了解决思路。最后，第4节对全文进行了总结。

2 研究进展

2.1 基于均匀圆阵的窄带近场源定位方法

针对均匀线阵下的远场辐射源DOA估计，形成了以基于线性预测类算法[34,35]、子空间分解类算法[36–40]和子空间拟合类算法[41–44]等一系列经典的方法。随着近场源定位在军事和民用领域需求的不断提升和重要性的不断凸显，国内外学者对其展开了深入的研究，取得了以基于2阶统计量的方法[45–49]和基于高阶累计量的方法[50–53]为代表的一系列丰硕成果。在引言中介绍了均匀圆阵相对于均匀线阵的结构优势，也正是考虑到这些优点以及对近场源3维定位的现实需要，围绕均匀圆阵下的近场源3维参数估计取得了卓有成效的成果。一方面是基于线阵下的方法发展演化而来的3维多重信号分类(MUltiple SIgnal Classification, MUSIC)方法[54]和高阶累积量方法[55,56]以及在此基础上改进后的降维方法；另一方面是通过空间模式变换，搭建起均匀圆阵与均匀线阵的桥梁，将均匀线阵下的方法推广运用到均匀圆阵上[57,58]；除此之外，基于均匀圆阵的阵元间相位信息反演得到近场源3维参数的方法[59,60]以兼具精准的估计和极低的计算复杂度受到广泛的关注。

2.1.1 基于2阶矩的近场源参数估计方法

MUSIC算法是最具代表性的一种空间谱算法，最早由Schmidt等人[36]提出，其核心思想是对任意阵列输出数据的协方差矩阵进行特征分解，得到信号子空间和噪声子空间，并利用两个子空间之间的正交性，通过谱峰搜索的方式确定辐射源信号的位置参数。后来Huang等人[45]将其引入到近场源定位场景，提出了一种联合角度和距离搜索的2维(Two Dimensional, 2D)MUSIC方法。Lee等人[61]进一步提出一种基于均匀圆阵的多维MUSIC算法实现近场源的3维参数估计，核心思想是基于线阵下的路径跟踪方法，首先将信号模型假设为远场辐射源信号参数估计模型，通过2D谱峰搜索获得角度估计值；其次，利用两者信号模型之间的代数关系式建立搜索路径，沿路径搜索谱峰，得到近场源的3维位置参数。Hayashi等人[62]通过盲源定标的方法对均匀圆阵的阵元互耦进行了校正，提高了近场源定位精度。

2.1.2 基于高阶累积量的近场源参数估计方法

相对于2阶统计量方法只能有效抑制服从高斯分布的加性白噪声，高阶累积量方法可以同时适用于非高斯噪声和高斯色噪声的处理。针对基于高阶累积量的近场源定位方法，最早由Challa和Shamsunder[51]提出了基于4阶累积量的总体最小二乘(Total Least Square, TLS)结合旋转子空间不变(Estimating Signal Parameters via Rotational Invariance Techniques, ESPRIT)的方法，尽管无需谱峰搜索，但高阶累积量的计算和参数配对的过程需要较大的计算度。吴云韬等人[63]提出一种基于高阶累积量的近场源方位、距离及频率3维参数的联合估计方法。此外，梁军利等人[64]还利用特殊的阵元接收数据构造高阶累积量矩阵，通过矩阵的特征值和特征向量完成了近场源参数的估计。上述都是基于线阵下的高阶累积量方法，胡增辉等人[65]将其推广到了均匀圆阵，通过构造的高阶累积量矩阵结合矩阵联合对角化得到阵列流形矩阵的估计，再利用近场和远场下方位角相同的结论得到方位角的估计，最后通过估计得到的阵列流形和方位角获得俯仰角和距离的估计。虽然算法估计精度较高，但高阶累积量和矩阵联合对角化的构造都带来了极高的计算代价。Mathews和Zoltowski[66]还提出了UCA-ESPRIT算法，算法通过模式空间变换将均匀圆阵转化为虚拟的均匀线阵，接着对转换得到的矩阵进行实值特征分解，通过特征值对应的特征向量得到信号源的角度估计，算法无需谱峰搜索，能够自动配对，但不能对辐射源的距离信息进行估计。

2.1.3 基于相位差的近场源参数估计方法

和前面提到的基于2阶统计量的方法和基于高阶累积量的方法相比，直接利用阵元接收数据的相位信息，通过多参数解耦实现辐射源位置参数的估计方法在计算复杂度上具有显著的优势，这一类方法将其统称为基于相位差反演参数估计算法[67]。在均匀圆阵下，Bae等人[68]提出一种带中心阵元的单近场源3维参数估计方法，利用中心对称阵元的共轭积解耦得到近场源的角度估计，随后利用中心阵元乘积得到距离参数的估计，算法分为两步完成对近场源3维参数估计的闭式求解，无需谱峰搜索，计算复杂度明显减小的同时还保留了高精度的参数估计。Wu等人[69]采用同样的两步估计方法，利用两组相关函数分别得到近场源的DOA和距离估计，算法无需中心阵元，但对阵元个数有严格的限制。Jung等人[70]对相位差反演参数估计算法作了进一步的改进，将原来的两步估计合成为一步，提出了一种仅利用1组相关函数的近场源3维参数估计闭式解方法，利用1对阵元接收数据的相位差结合最小二乘算法就能直接得到近场源的3维参数估计，算法步骤更加简单，计算复杂度得到进一步减小，同时放宽了对阵元个数的要求。Liu等人[71]对相位差反演参数估计算法做了进一步的推广，利用频谱峰值来获取相位差信息，使其能适用于对多个非相干近场源的3维参数估计。Ma等人[72]在通过MUSIC方法获得方位角的基础上，通过相位差之间的代数关系来估计俯仰角和距离，实现在均匀圆阵下近场源的高精度定位。

2.2 基于均匀圆阵的近场源定位解模糊方法

当阵列的孔径大于辐射源的半波长时，相位模糊会导致辐射源位置参数的算法估计失效[73–75]。在基于均匀线阵下的参数估计中，Sundaram等人[76]提出求模转换方法，该方法通过逐步减少最长基线的相位差中模糊量实现解模糊。Zheng等人[77]提出旋转基线方法，该方法通过计算位置参数在量化函数的最大值实现解模糊。在基于均匀圆阵下的参数估计中，王伟等人[78]提出一种循环搜索解模糊的远场源参数估计算法，由于真实相位差具有正弦特性，通过遍历可以得到无模糊的相位差。潘玉剑等人[79]采用三角函数化简得到由远场源位置参数构成的复数，结合距离的聚类算法可以得到无模糊参数。为了解决上述方法计算复杂度较大和近场源定位等问题，作者团队提出了基于旋转短基线的解模糊方法。此外，为了同时解决定频和调频近场源定位的问题，作者团队提出了一种基于模糊度搜索下多子阵结果聚类的解模糊算法。

2.2.1 基于旋转短基线的解模糊方法

针对近场源定位，作者团队提出一种利用旋转均匀圆阵形成虚拟短基线的解模糊算法[80]。首先，利用均匀圆阵中心阵元的初始相位差对其他阵元旋转前后的两组数据进行相位补偿；随后，在通过阵元的复共轭积计算旋转前后无模糊相位差的基础上，使用最小二乘法反演出近场源的方位、俯仰和距离等3维位置参数；最后，利用无模糊近场源位置参数消除旋转前次长基线阵元间的相位差模糊，得到长基线下的高精度3维位置参数。相比于文献[81]中基于MUSIC算法下的旋转解模糊方法，利用相位差解模糊方法的计算复杂度更小，但是需要接收旋转前后两组数据，因此只适用于频率不变的定频近场源的参数估计。

2.2.2 基于多子阵结果聚类的解模糊方法

为了解决旋转短基线方法只适用于定频近场源参数轨迹场景，作者团队提出了一种基于模糊度搜索下多子阵结果聚类的解模糊算法[82]，该方法能够同时解决定频和调频近场源定位场景。首先，由于模糊是近场源的角度参数引起的，考虑到接收数据中角度和距离参数相互耦合对解模糊造成的困难，算法利用中心对称阵元的相位差将近场源的角度和距离进行解耦；随后，通过无模糊的相位差得到仅由角度参数构成的复数，将中心对称阵元的相位差经过模糊度遍历搜索得到包含无模糊相位差的矩阵，该矩阵的每列均包含由真实角度构成的复数；随后，通过基于欧氏距离的聚类方法可以搜索到真实角度对应的复数，进而反演出近场源的真实角度估计；最后，利用真实角度估计结果对长基线下的相位差参数估计解模糊，得到近场源3维位置参数估计。基于模糊度搜索下多子阵结果聚类解模糊算法能够解模糊的范围广，并且计算复杂度较小，估计的性能较好。

2.3 基于均匀圆阵的近场LFM信号定位方法

在综合现有的宽带和窄带下近场源参数估计算法的基础之上，作者团队从时域、频域、分数阶傅里叶域将均匀圆阵下的宽带LFM信号进行窄带化处理，通过多种方式提取窄带化模型下的相位信息，建立了相邻阵元相位差与近场源位置参数对应的数学关系，结合相位差反演参数估计算法，提出了基于聚焦变换的近场LFM信号定位方法、基于分数阶傅里叶变换的近场LFM信号定位方法以及基于时延的近场LFM信号定位方法，并对所提算法的性能进行分析和比较。

2.3.1 宽带辐射源窄带化处理方法

宽带辐射源信号相对于窄带辐射源信号更有利于目标检测、参量估计和目标特征提取等因此国内外专家学者对宽带辐射源信号处理技术进行了深入的分析和研究，形成了以基于统计推断和基于信号子空间方法为主体的宽带高分辨测向算法。

基于统计推断的方法中最具代表性的就是贝叶斯估计方法[83]和最大似然估计(Approximated Maximum Likelihood, AML)方法[84]，且后者是前者在白噪声情况下的一个特例。AML宽带信号估计算法是将窄带信号确定性和随机性最大似然估计器推广运用到宽带信号中，本质上依然是一种非线性最优化算法，优化过程相对于窄带信号更加复杂，运算量更大。Agrawal等人[85]提出了一种宽带迭代2次型最大似然(Iterative Quadratic Maximum Likelihood, IQML)算法，将宽带信号分解成若干个窄带信号和的形式，建立宽带下的ARMA(AutoRegressive-Moving Average)模型，并对各个窄带频点进行角度粗估计，然后运用最小二乘算法对角度估计值进行优化改进。Cadalli等人[86]提出改进的期望最大(Estimate-Maximize, EM)算法，用正则化最小二乘方法结合树结构对信号进行估计，相比于传统EM算法具有更好的估计性能。Jin等人[87]将AML的谱函数视为恒定比例的目标分布，提出了完美采样的马尔可夫蒙特卡罗方法实现宽带辐射源的角度估计，相比于传统的AML方法，该方法能够降低计算复杂度，同时还能适应低信噪比(Signal-to-Noise Ratio, SNR)的情况。尽管国内外许多专家学者提出了若干减少多维优化过程降低算法运算量的改进AML算法，但这些算法大都是针对特定的情况具有一定的局限性，无法掩盖AML算法本身因多维优化过程带来的计算复杂度极高，易收敛到局部极值导致结果出错等问题，因而难以在实际中得到应用。

基于信号子空间类算法是将窄带下的子空间算法推广到宽带辐射源信号参数估计中，相对于统计推断类算法，计算复杂度得到了极大的改善，也吸引了众多国内外专家学者的关注和研究，其主要可以分为非相干信号子空间方法(Incoherent Signal-Subspace Method, ISSM)[88–90]和相干信号子空间方法(Coherent Signal-Subspace Method, CSSM)[91,92]。在ISSM类方法中，Wax等人[89]最早提出的方法处理方式比较简单，就是将宽带辐射源信号在频域进行分段，将划分的每段视为窄带信号，利用窄带下的高分辨参数估计方法对每个子段进行DOA估计，最后将各段的估计结果进行汇总，加权求和得到最终的估计结果，但是由于该方法仅利用了宽带信号的部分信息，加权系数也难以合理有效，导致估计性能不高同时还不能适用于相干宽带辐射源信号的参数估计，每段数据的高分辨处理也带来了较大计算量。于红旗等人[93]提出了基于频域子空间正交性测试(Test of Orthogonality of Frequency Subspaces, TOFS)方法，通过角度和频率构造各频点噪声子空间的正交性程度来得到DOA估计，算法无需参考频点的投影变换，避免了伪峰的出现，并降低了计算量。

针对ISSM算法存在的问题，Wang等人[94]引入“聚焦”的思想，提出了CSSM算法，该方法同样将宽带辐射源信号在频域划分为多个子频段，通过构造“聚焦”转换矩阵，将各个子频段的协方差矩阵聚焦到参考频点上，得到平均聚焦协方差矩阵，利用该矩阵结合窄带下高分辨参数估计算法得到宽带辐射源信号的DOA估计。顾名思义，CSSM算法的聚焦转换类似于空间平滑，能够处理相干辐射源信号的参数估计，估计精度比ISSM算法高，计算复杂度比ISSM算法小。经典的CSSM类算法有：旋转信号子空间(Rotate Signal Subspace, RSS)变换算法[95]、信号子空间变换(Signal Subspace Transform, SST)算法[96]以及双边相关变换(Two side Correlation Transformation, TCT)算法[97]。尽管CSSM算法在估计精度和计算复杂度上有较大程度的改进，但是其需要辐射源位置参数的先验估计和聚焦频点的预选择，并且算法性能受预估计误差的影响较大。

2.3.2 基于聚焦变换的近场LFM信号定位方法

传统的基于聚焦变换的宽带信号参数估计算法在获得聚焦协方差矩阵后均采用基于谱峰搜索的MUSIC算法估计得到辐射源信号的参数信息，如果延用3D-MUSIC算法，计算复杂度将成倍增加。相较而言，基于相位差反演的近场LFM信号3维位置参数估计方法具有在计算复杂度和估计精度上的优势。因此，将聚焦协方差矩阵和相位差反演参数估计算法结合起来，能够实现快速的近场LFM信号参数估计。瞄准非相干宽带近场LFM信号的3维位置参数估计问题，作者团队在双边相干变换算法的基础之上对其加以改进，无需LFM信号位置参数的先验信息，突出算法对宽带近场LFM信号参数估计的精准性和实时有效性[98]。首先，将阵元接收到的数据在频域进行展开，通过带通滤波器将不同频带的数据进行分离；接着，将分离后的各组数据在时域进行分段，并将各段数据变换到频域；然后，选取聚焦参考频点，利用各频点接收数据的协方差矩阵和聚焦频点的协方差矩阵构造聚焦转换矩阵，并通过聚焦变换获得聚焦频点下的协方差矩阵；紧接着，提取聚焦协方差矩阵副对角线上元素的相位构造相邻阵元接收数据的相位差；最后，结合相位差反演参数估计算法得到宽带近场LFM信号的3维位置参数的估计值。对于聚焦变换方法的计算复杂度，在频域展开中需要O(KMNlg(MN))，在协方差矩阵特征分解中需要O(KJM2)，在相位差反演3维参数估计中需要O(K(M −1)M)，其中K表示近场LFM信号数，N表示接收数据的快拍数，M表示均匀圆阵的阵元数，J表示分段数。由于基于聚焦变换方法通过提取平均聚焦协方差矩阵副对角线元素的相位，并与相位差反演参数估计算法建立连接，能够快速准确地获得宽带近场LFM信号3维位置参数的估计值，计算复杂度得到了极大的降低，能够满足实际应用中对实时性的要求。

2.3.3 基于分数阶傅里叶变换的近场LFM信号定位方法

针对非相干的宽带近场LFM信号，利用其在分数阶傅里叶域的能量聚焦性，作者团队提出了基于FRFT的宽带近场LFM信号3维位置参数估计算法[99]。算法首先将阵列传感器接收到的时域数据变换到分数阶傅里叶域，观察LFM信号在分数阶傅里叶域形成的谱峰个数，确定非相干宽带近场LFM信号的个数；接着，提取出LFM信号在分数阶傅里叶域的峰值及其相位信息，根据无模糊范围条件判断提取的相位是否存在模糊；对于无模糊的相位，直接计算相邻阵元相位差矩阵，建立其与相位差反演参数估计算法的连接；对于存在模糊的相位，计算中心对称阵元的相位差，利用解模糊方法得到宽带近场LFM信号无模糊的角度估计，利用得到的角度粗估计值解相邻阵元相位差的模糊，得到更高精度的LFM信号角度估计和剩下的距离估计。由于算法对信号模型的导向矢量做了近似处理，因此算法估计结果与真值存在偏差。相对于传统的谱估计方法，计算复杂度得到了极大的降低，但分数阶傅里叶域峰值点搜索需要消耗一定的时间，对单个LFM信号位置估计的计算效率低于基于聚焦变换的算法，但针对多个非相干的宽带LFM信号，算法无需采用带通滤波器对LFM信号进行分离，降低了硬件成本。对于基于FRFT的近场LFM信号定位方法的计算复杂度，在分数阶傅里叶变换中需要O((M+1)N4)，在计算相邻阵元相位差矩阵需要O(KM)，在相位差反演3维参数估计中需要O(K(M+1)M)。

为了验证解模糊的有效性，将基于FRFT算法的3维位置参数估计的均方根误差(Root Mean Square Errors, RMSE)与基于聚焦变换(FOcus SHift, FOSH)算法以及基于FRFT结合3维MUSIC方法(FRFT-3DMUSIC)进行了对比。从图2可以看出，基于FRFT结合3维MUSIC算法的无模糊估计范围比相位差反演参数估计算法更广，能够实现对超过无模糊估计阈值频率的LFM信号的精确参数估计。此外，基于聚焦变换和基于FRFT定位算法对超过无模糊估计阈值频率的LFM信号进行3维位置参数估计时，会出现相位模糊的情况，导致算法失效。在采用解模糊算法后，基于FRFT的算法和基于聚焦变换的算法均能实现对LFM信号3维位置参数的无模糊估计，从而证明了算法采用解模糊方法后对超过无模糊估计阈值频率的LFM信号进行定位的有效性。

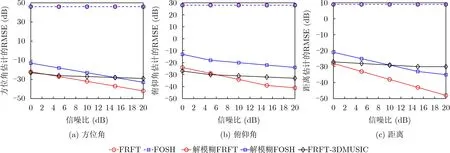
图2 近场LFM信号3维位置参数估计的RMSE

2.3.4 基于时延的近场LFM信号定位方法

针对非相干宽带近场LFM信号的高频段大带宽的定位问题，作者团队结合“去斜”的基本原理，直接在时域对LFM信号进行时延混频处理，通过输出的单频信号建立新的类窄带信号模型，通过提取类窄带信号模型下频域输出的峰值实现对非相干LFM信号的分离，同时利用峰值相位构建相邻阵元相位差矩阵建立与相位差反演参数估计算法的联系，得到LFM信号3维位置参数的估计值[100]。对于基于时延的宽带近场LFM信号定位方法的计算复杂度，在建立类窄带信号模型中需要O(M(N −N1))，在计算相邻阵元相位差矩阵需要O(K(M −1))，在相位差反演3维参数估计中需要O(K(M −1)M)，其中N1为时延的快拍数。各类方法单次运行的时间如表1所示，可以看出，基于时延的算法耗时最少，基于分数阶傅里叶变换算法和ISSM-3DMUSIC算法的计算复杂度相对较大。

表1 单次运行平均时间对比(s)

3 展望

本文主要围绕均匀圆阵下的非相干近场源定位进行研究，但是实际环境下，因为多径效应等因素会产生完全相干或部分相干的辐射源信号同时入射到阵元的情形，因此需要考虑能够估计相干辐射源位置参数的算法。其次，入射到阵元的宽带辐射源信号并非只处于阵列的近场菲涅尔区，可能存在近场和远场辐射源同时存在的情形，此时需要算法能够对近远场混合辐射源进行分类识别并估计出相应的位置参数。

3.1 相干辐射源信号参数估计问题

辐射源定位会受到多径效应的影响，由此将带来阵元同时接收到多个相干宽带辐射源信号的情形，此时需要定位算法能够从多个相干的宽带辐射源耦合数据中分离并估计得到各个辐射源的位置参数，并结合先验信息判断得出真实的宽带辐射源的位置信息。针对相干辐射源的参数估计问题，现有文献主要针对线阵下的远场窄带辐射源信号，提出了以空间平滑、矢量矩阵重构为代表的解相干算法。对均匀圆阵下的宽带相干辐射源解相干参数估计的思路包括以下两方面，一方面是将均匀圆阵接收到的宽带数据经过窄带化处理后通过相位模式激励的方法变换为虚拟的均匀线阵，借鉴线阵下空间平滑以及矢量矩阵重构等解相干方法实现对相干宽带辐射源的位置参数精确估计；另一方面是考虑通过水平或者垂直移动均匀圆阵，使得移动前后的均匀圆阵接收数据间的相位差满足Vandermonde结构形式，从而可以实现平滑解相干。

3.2 近远场混合源参数估计问题

相对于单独的远场或者近场源，近远场混合源的参数估计研究起步较晚，且主要针对窄带下的近远场混合源参数估计问题展开研究。现有的近远场混合源参数估计技术主要采用基于特征子空间的方法，大体可分为两类：一类是同时获得远场和近场源的角度的估计值，通过1维谱峰搜索实现混合源的识别和近场源的距离估计[101–103]。另一类则是首先对近场源和远场源进行分离，并分别对远场源的角度以及近场源的角度和距离进行估计[104,105]。但是相对于窄带信号，宽带近远场混合源信号的很多特性都发生了改变，无法将窄带下的近远场混合源参数估计方法直接拓展运用到宽带辐射源中，需要探索新的参数估计方法或者建立起窄带和宽带下近远场辐射源信号的对应方式，结合深度学习方法[106,107]实现宽带近远场混合源参数估计。

4 结论

针对均匀圆阵下近场源定位问题，本文梳理了通过2阶矩、高阶累积量和相位差反演的定位方法，以及通过旋转短基线和多子阵结果聚类解模糊方法。在利用统计推断和基于信号子空间方法将宽带信号窄带化的基础上，本文系统阐述了分别利用聚焦变换、分数阶傅里叶变换和时延实现近场线性调频信号高效精准定位方法，并分析比较了算法的优缺点。最后对相干辐射源和近远场混合源参数估计等后续研究内容进行了展望，为研制辐射源定位系统提供技术支撑。