一种水下体目标高精度长基线定位方法
2023-03-01孙大军李宗晏郑翠娥
孙大军 李宗晏 郑翠娥
(哈尔滨工程大学水声技术重点实验室 哈尔滨 150001)
(海洋信息获取与安全工信部重点实验室 哈尔滨 150001)
(哈尔滨工程大学水声工程学院 哈尔滨 150001)
1 引言
长基线定位作为一种高精度的技术手段,广泛地应用于水下航行器定位[1–4]。国际上知名的高精度长基线定位设备有英国Sonardyne的Fusion 6G、挪威Kongsberg的cPAP、法国iXblue的Ramses等,均在海洋工程领域取得了广泛的应用[5–7]。
近年来国内外学者对长基线定位技术开展了深入研究[8]。文献[9]针对泰勒级数展开法依赖初始参考值的问题,通过Chan算法解算求得初始参考值,兼顾了解算精度和解算效率。为了克服“询问-应答”测量系统应用中的不足,文献[10,11]通过在水下航行体上安装合作声信标的方式,提高了水下运动目标的定位精度。文献[12]通过水面浮标和水下信标结合的阵型修改阵型拓扑结构,提升了定位性能。文献[13]通过增加基站数量提高测点冗余度的方式提升定位精度。以上研究工作分别从算法特性、长基线的信号量测模式、阵型结构设计等方面优化了长基线定位性能,证明了水下长基线3维定位可以达到米级甚至亚米级的精度。然而,目前仍然存在许多因素制约着长基线定位精度的进一步提高。
传统长基线定位场景中目标总被简化为质点模型。而实际情况下存在几何尺度大(口径达到几米)、运动姿态未知的体目标,若继续使用质点长基线定位模型,会带来较大的模型误差,无法满足高精度定位需求。目前针对该问题还没有有效的解决途径。
针对上述问题,本文通过引入体目标姿态、位置联合估计,消除了传统质点算法的模型误差,实现体目标高精度定位。本文从以下4部分展开:第1部分从长基线定位原理出发,分析长基线定位精度的影响因素;第2部分理论分析质点模型对体目标定位精度的影响关系;第3部分提出一种基于体目标姿态、位置联合估计的长基线定位方法,并进行了性能分析;第4部分通过计算机仿真定量评价本文方法对体目标的定位精度,证实了本方法的优势。
2 传统长基线定位模型与体目标的适配性分析
2.1 传统长基线定位模型及误差分析
长基线定位系统由预置于水下的参考声信标和安装于被定位目标上的测距仪构成,由声信号的传播时间来确定目标和各参考声信标之间的距离,通过距离交汇解算目标位置,如图1所示。
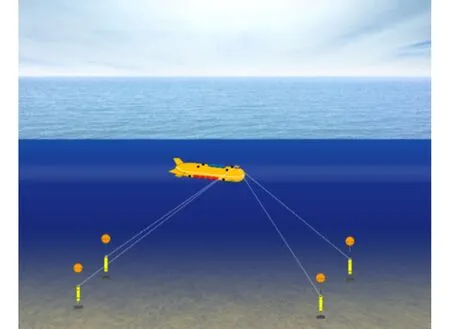
图1 长基线定位系统
对传统长基线定位,将目标当作质点基于球面交汇原理构建量测方程,通过最小二乘估计求解目标位置
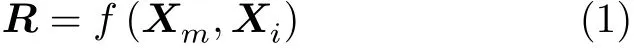
其中,R为 测 量 斜 距,f(a,b) 为//a −b//2,Xm=[xm,ym,zm]T为目标的位置坐标,Xi=[xi,yi,zi]T为参考声信标的位置坐标,T代表转置。
将式(1)在初值Xm0处进行线性化后,得到如式(2)的目标位置的矩阵表达形式为
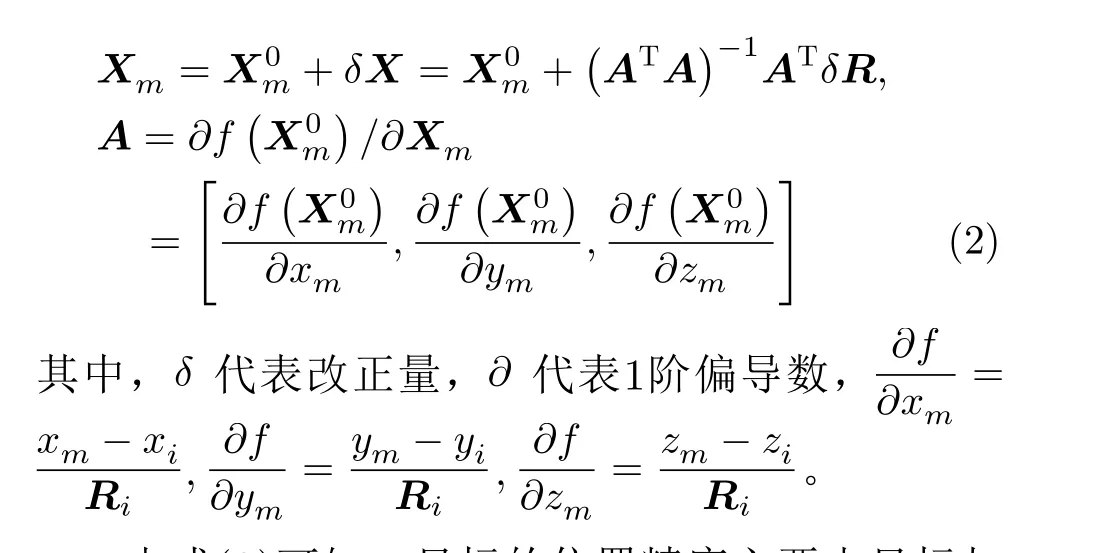
由式(2)可知,目标的位置精度主要由目标与长基线阵型的相对位置关系和测距精度决定。
2.2 传统长基线模型与体目标的适配性分析
试验工况参考文献[13],如图2所示,信标布放海底,目标位于基阵中心处。区别在于文献中被定位的目标为质点目标,而本文为体目标。体目标模型如图3所示,其上均匀安装了一圈发射换能器(声源),红色换能器为1号声源,其余声源按照逆时针排序。由于换能器的指向性和体目标自身遮挡问题,不同声信标接收体目标上不同声源的信号,如第i个长基线信标接收体目标上第k个换能器的信号,i̸=k。o为 体目标质心,r1i为 参考声信标i到体目标质心的距离,r2i为 参考声信标i到体目标上声源的距离,r0为体目标质心到声源的距离。

图2 体目标试验工况
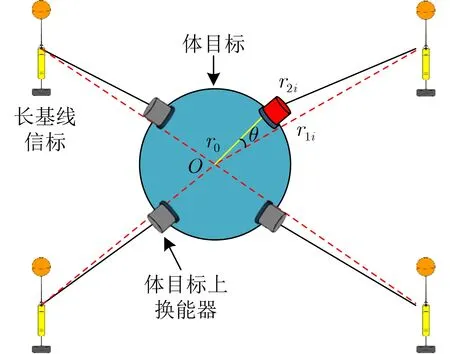
图3 体目标模型
对于几何尺寸较大的体目标,通常用几何中心来描述位置。体目标的几何中心与其上对称安装的换能器基阵中心重合。由于体目标上各发射换能器与几何中心不重合,做质点模型处理时,带来距离误差dR
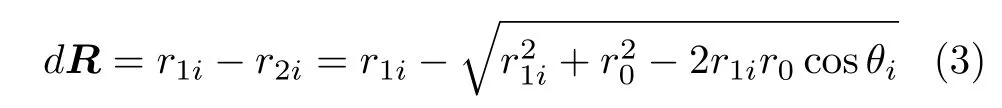
其中,θi为信标到体目标质心和体目标质心到声源之间的夹角,其余弦取值范围为[ 0,1],与体目标的姿态、半径、体目标与长基线信标几何位置关系均有关。且模型误差与夹角余弦正相关,当cosθi=1时,质心、换能器、信标共线,此时距离的模型误差为r0,即体目标半径。
模型误差到定位误差的传播公式[14]为
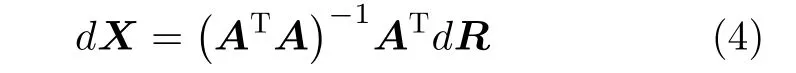
其中,dX为目标的3维位置误差,A参照式(2)。
由此,对体目标采用传统长基线模型解算时,主要误差因素有目标与长基线阵型的相对位置关系、体目标半径、体目标姿态等。由于测距误差是长基线定位的主要误差来源,当体目标的半径与测距精度需求相比拟时,模型误差不可忽略,须修正解算模型以解决体目标模型失配问题。
3 基于体目标姿态、位置联合估计的长基线定位方法
为解决上述问题,本文提出基于体目标姿态、位置联合估计的定位解算方法。本方法引入体目标姿态、位置联合估计,得到地理坐标系下体目标上各发射换能器与几何中心的关系,消除了传统质点算法的模型误差,解决了体目标姿态未知问题,实现体目标高精度定位。
3.1 体目标坐标系建立与旋转
假设各换能器与体目标刚性连接,相对位置关系恒定,此时可构建体目标坐标系。引入体目标坐标系相对于地理坐标系的姿态参数,即可确定换能器在地理坐标系下的空间位置。体目标坐标系定义参照地理坐标系,如图4所示。
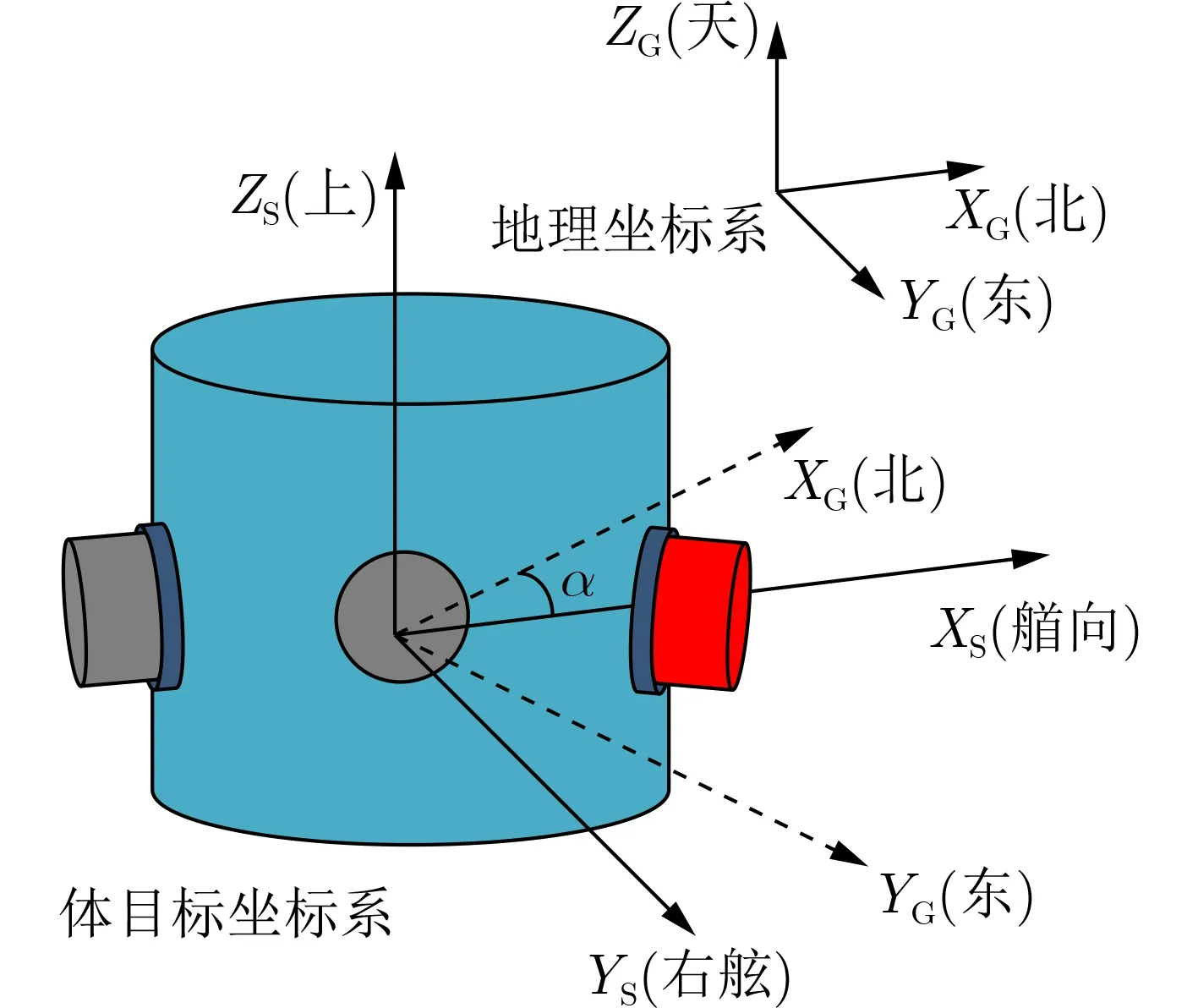
图4 体目标坐标系建立
地理坐标系XG轴指向北方向,YG轴指向东方向,ZG轴 指向天方向,记为O-XGYGZG;体目标坐标系以体目标质心为原点,XS轴指向体目标艏向,YS轴 指向体目标右舷向,ZS轴指向体目标上方向,记为O-XSYSZS。其中体目标艏向为体目标质心到体目标上红色(1号)换能器的朝向。

其中,φk为体目标上第k个换能器与XS轴的夹角,当体目标均匀安装6个换能器时,φk=60◦·(k −1),k=1,2,...,6。
上述两坐标系夹角即体目标姿态参数α,β和γ,从地理坐标系旋转到体目标坐标系时,依次绕Z,Y,X轴分别旋转α,β,γ角度,参照文献[15]得到的旋转矩阵为
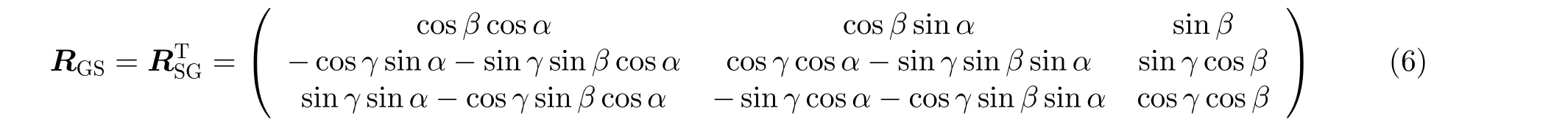
3.2 体目标长基线定位模型
下面建立体目标姿态、位置联合解算模型,此模型的待求参数为体目标质心在地理坐标系下的坐标和体目标姿态,此时以距离为量测量的观测方程如式(7)
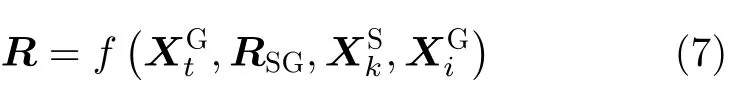


3.3 体目标方法的误差分析
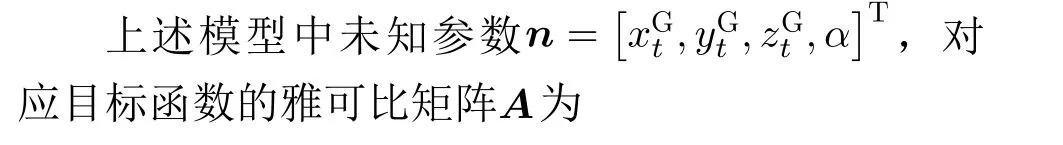

算法1 体目标长基线定位方法
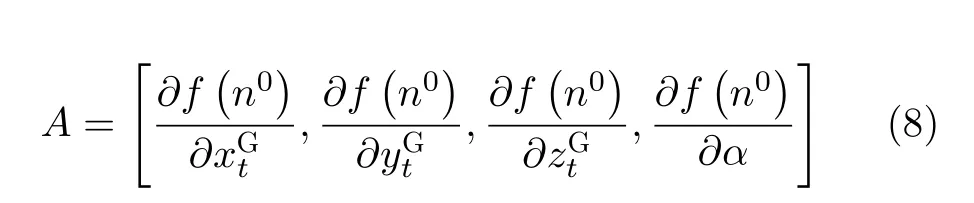
其中
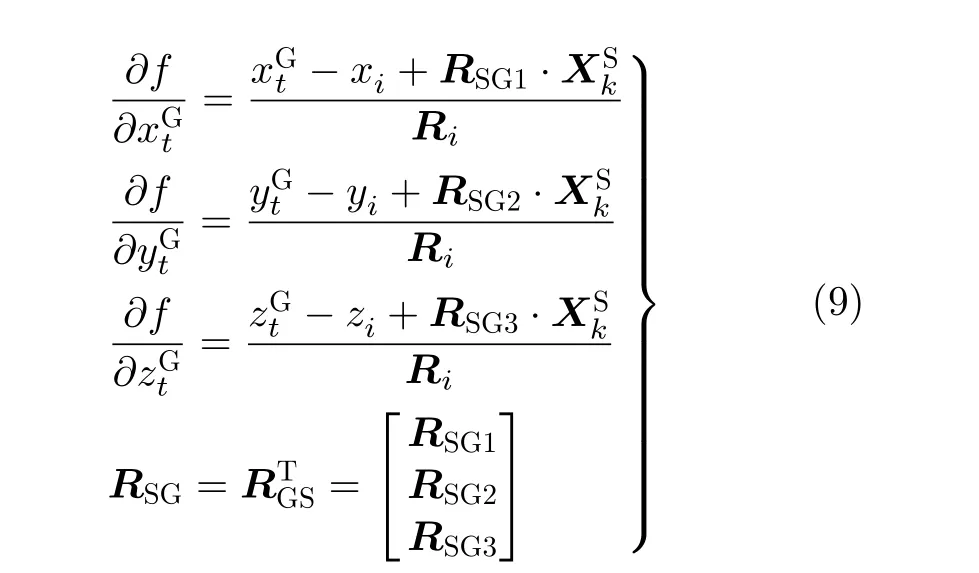
其中,RSG为体目标坐标系到地理坐标系的旋转矩阵
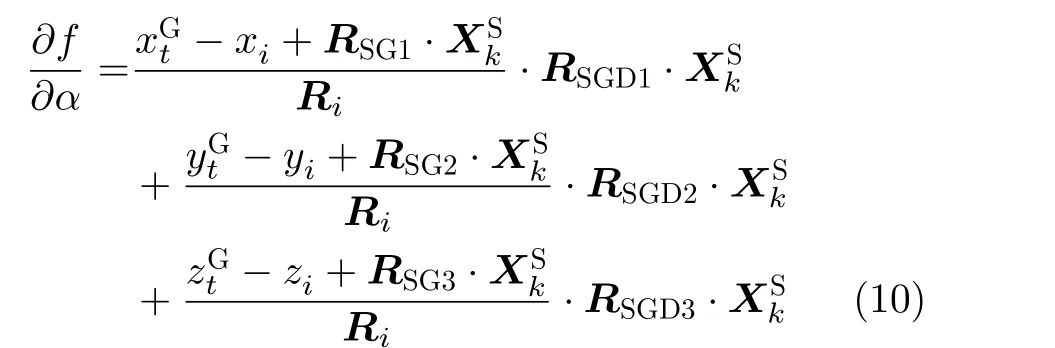
其中
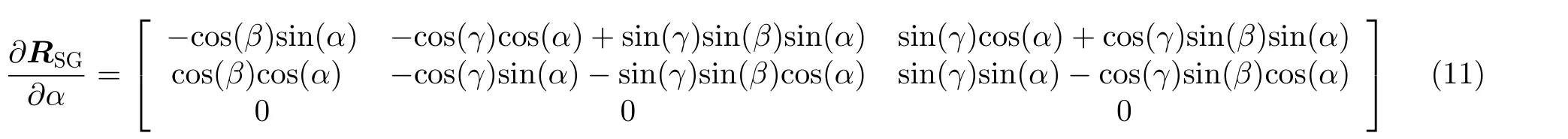
体目标长基线定位的误差传播公式同式(4)。
因此,影响体目标长基线定位精度的因素主要有体目标与长基线阵型的相对位置关系、体目标半径、体目标姿态以及测距精度。在其他条件确定的前提下该方法的定位性能受制于测距精度。
3.4 优势分析
针对质点模型对体目标失配问题,本文先构建体目标坐标系,并引入体目标姿态参数,得到地理坐标系下体目标上各发射换能器与几何中心的关系,后通过体目标姿态、位置联合估计,得到一种体目标长基线定位方法。相较于传统的质点长基线定位方法,本文方法具有以下优势:
(1)消除模型误差。本文的体目标定位模型相较传统定位模型,加入了RSG和XkS两个参数,从而在定位方程中将体目标上每个换能器转换到体目标的质心处,消除了模型误差。同时,本模型中若姿态已知,该方法可以直接得到体目标上不同换能器的地理位置;若姿态未知,通过求解出体目标质心位置和姿态后,即可得到体目标上不同换能器的地理位置。
(2)解决姿态未知问题。定位模型中新增的RSG和体目标姿态参数有关,但此时体目标的姿态和质心位置均是未知的,本文方法同时估计体目标姿态、位置,解决姿态未知问题。
综上,本方法在定位模型和求解参数上进行改进,建立了体目标定位模型,消除了模型误差,同时估计体目标姿态,解决体目标姿态未知问题。
4 仿真分析
为了验证本文提出的体目标长基线方法的可行性,并与传统长基线方法对比,进行了仿真试验。仿真条件如下,以8只长基线信标布置长基线阵,具体如图5(a),阵型设计为1 km×1 km的正方形,水深500 m。体目标在长基线阵型的几何中心处,其质心坐标(0,0,400) m。体目标自身状态如图5(b),其质心为P0点,并在圆周上均匀装有6个换能器,分别为P1到P6,体目标半径为5 m。其初始状态如下所示,以质心为原点6个换能器刚性连接,建立体目标坐标系,P1为1号基元,其在体目标坐标系与x轴的初始角度φ为0°。体目标坐标系与地理坐标系的姿态角α,β,γ均为0°。
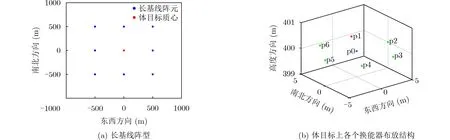
图5 仿真基本场景
由表1可知,体目标位于阵中心时,本文方法不存在定位误差,而传统方法存在较大的定位误差,且所有误差均体现在垂直方向。
由于未加入随机误差,此时影响传统方法定位精度的仅有模型误差。故目标位于基阵中心时模型误差均传递到垂向定位误差上,此时垂向定位误差达到32 m,模型误差不可忽略。相较于传统方法,本文方法消除了模型误差,提高了定位精度。
在后文的仿真中,先分别从体目标与长基线阵型的相对位置关系、体目标半径、体目标姿态、测距精度独立对比分析两种算法的定位性能,后结合实际工况,分析两种算法在各因素耦合时的性能表现。
4.1 仿真试验1:独立因素变化下的定位精度
4.1.1 体目标与长基线阵型几何位置关系影响
首先分析体目标位于长基线阵型中不同位置的情况。长基线阵型结构固定,待测体目标位于长基线阵型偏心处(300,300,400)m,其他仿真条件同上,表2为体目标位于阵型偏心处两种方法的定位误差。
由表2可知,体目标位于阵偏心处时,本文方法不存在模型误差,而传统方法存在较大的定位误差,且水平和垂直方向均存在定位误差,此时垂直定位误差从32 m减小到21 m。
综合表1、表2可知:(1)传统方法下定位误差与体目标和长基线阵型的相对位置有关,并非恒定量;(2)传统方法下在阵内时水平定位误差相较垂直定位误差较小;(3)相同仿真条件下本文方法不受几何位置关系的影响,定位误差均为0 m。

表1 体目标位于阵型中心处定位误差(m)

表2 体目标位于阵型偏心处定位误差(m)
4.1.2 体目标半径的影响
然后分析体目标半径对两种方法定位结果的影响。体目标半径从1 m变化到8 m,其他仿真条件同上。由于体目标位于阵型中心处两种方法水平定位误差均极小,故仅观察垂直定位误差。两种方法定位结果如图6所示,传统方法垂直定位误差随着半径增大而近似线性增大,半径达到5 m时,定位误差已达到32 m,本文方法不受体目标半径的影响,定位误差均为0 m。
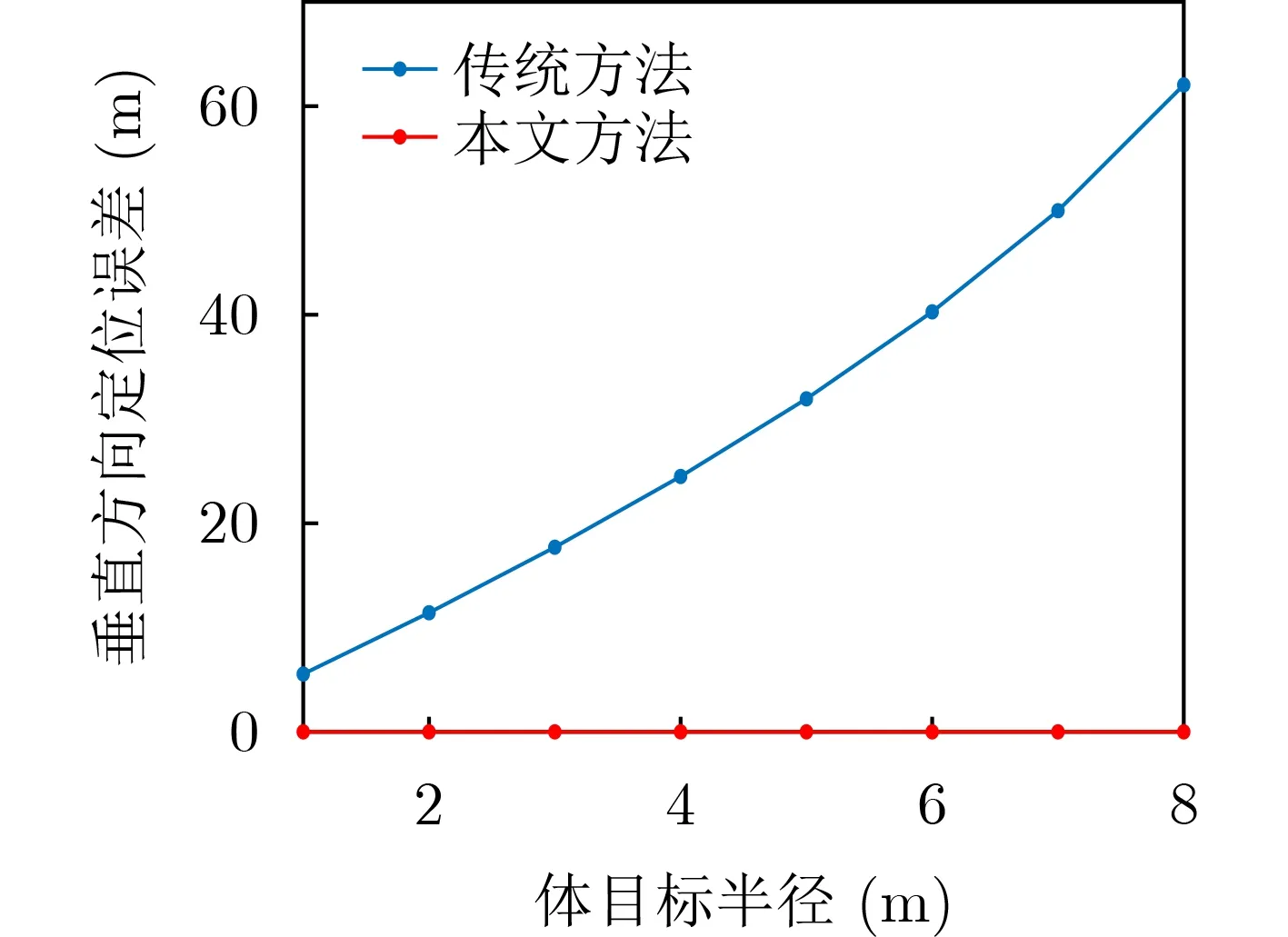
图6 垂直定位误差与体目标半径的关系
4.1.3 体目标姿态的影响
接下来分析体目标初始姿态对两种方法定位结果的影响。体目标初始姿态从0°变化到60°,其他仿真条件同上。两种方法定位结果如图7所示,在半径固定时,传统方法受目标初始姿态影响较小,不同姿态下定位误差在31.9~32.4 m附近,本文方法不受初始姿态的影响,定位误差均为0 m。
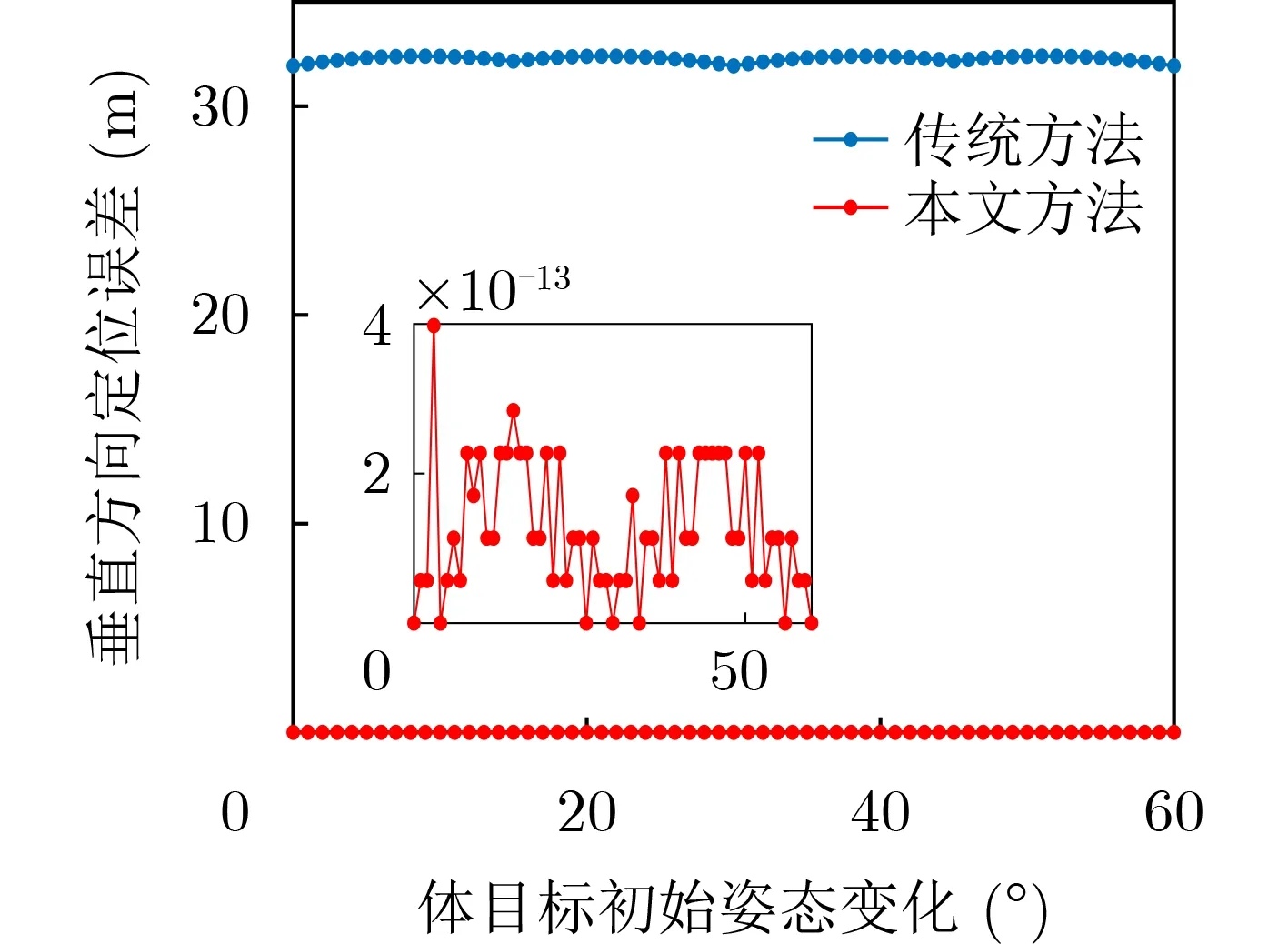
图7 垂直定位误差与目标姿态的关系
4.1.4 测距误差的影响
最后分析测距误差对两种方法定位结果的影响。测距误差从0.1 m变化到0.5 m,其他仿真条件同上。假设测距误差服从零均值高斯分布,进行200次蒙特卡罗仿真。两种方法定位结果如图8所示,本文方法水平定位误差数值上与传统方法相当,定位误差均随测距误差线性增大。本文方法在测距误差0.5 m时,垂直定位误差达到1 m,远优于传统方法的32 m。
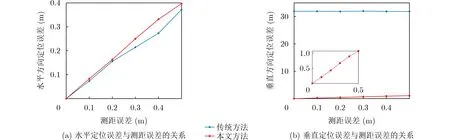
图8 定位误差与测距误差的关系
4.1.5 小结
本节分别针对体目标与长基线阵型的相对位置关系、体目标半径、体目标姿态、测距误差等因素对两种方法进行仿真试验,本文方法定位精度均优于传统方法。
从仿真结果看出传统方法定位的模型误差与体目标与长基线阵型的相对位置关系、体目标半径、体目标姿态均有关。体目标和长基线阵型的相对位置关系主要影响模型误差到定位误差的传递方向;体目标半径的尺度直接影响模型误差的大小,半径大尺度下模型误差不可忽略。
同时也能看出本文方法相较传统方法消除了模型误差,故受体目标半径和姿态影响较小,但本文方法和传统方法的定位误差同时受测距误差的影响。
4.2 仿真试验2:实际工况下的定位精度
在实际工况下,体目标与长基线阵型的相对位置关系、体目标半径、测距误差等因素均是固定的,仅体目标初始姿态未知。下面针对实际工况,分析此时两种方法的定位精度。仿真条件如下,长基线阵型结构固定,阵型设计为1 km×1 km的正方形,体目标位于阵型中心处,测距精度0.2 m,体目标半径5 m,体目标初始姿态从0°变化到30°,其他仿真条件同上。假设测距误差服从零均值高斯分布,进行200次蒙特卡罗仿真,在此工况下两种方法的定位结果如图9所示。在测距精度0.2 m,体目标半径5 m,初始姿态0~30°的条件下,本文方法相较传统方法水平定位精度基本相同,最大相差2 cm。垂直定位精度从32 m提高到0.5 m,达到了亚米级定位精度。
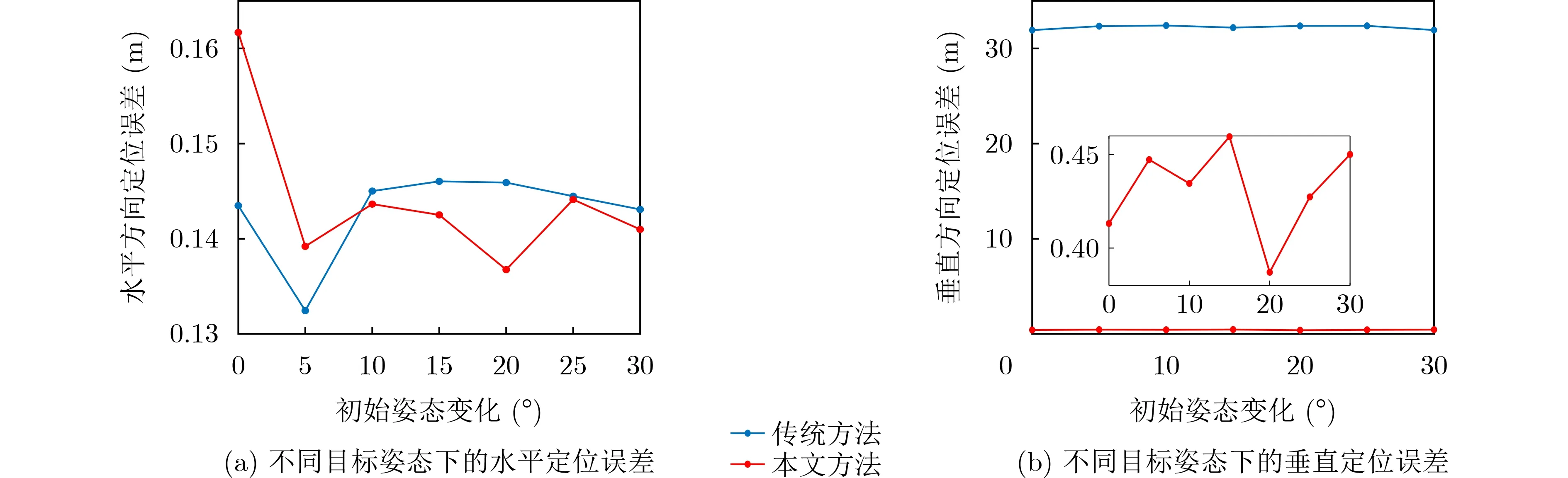
图9 实际工况下不同目标初始姿态的定位误差
5 结论
本文针对水下体目标几何尺度大、姿态未知等因素,导致传统长基线定位模型不适配、难以实现高精度定位的问题,基于体目标上各点刚性连接、相对运动状态恒定的特性,引入了体目标姿态位置联合估计,获得一种针对水下体目标的定位解算方法。通过理论分析证明体目标半径大尺度下模型误差不可忽略的问题。并且用仿真表明了本文的体目标长基线定位方法可以达到亚米级定位精度。本文提出的定位方法和分析方式可为其他类型水下体目标的定位方法、精度分析提供参考。
