基于迁移深度强化学习的低轨卫星跳波束资源分配方案

陈前斌 麻世庆 段瑞吉 唐 伦 梁承超

(重庆邮电大学通信与信息工程学院 重庆 400065)

1 引言

宽带卫星通信系统由于其通信覆盖面广、终端架设快捷、稳定性高等特点，是全球信息高速公路的重要组成部分，也是空天地一体化的重要发展方向。作为宽带卫星通信系统的核心技术之一，多波束天线技术在波束成形和波束扫描方面具有高灵活性，目前已经广泛应用于实际卫星通信系统。低轨道(Low Earth Orbit, LEO)卫星通信系统是近年来应用多波束天线技术的热门卫星系统之一，也是未来空天地一体化的优化发展方向，对完善空天地一体化网络具有重要作用[1]，LEO卫星网络的进步也引起了工业界和学术界的广泛关注[2,3]。传统的LEO多波束技术平等分配带宽资源和功率资源，该方案星载资源损耗大，资源利用率低，容易造成特定小区资源分配策略无法满足通信需求。跳波束(Beam Hopping, BH)技术通过相控阵技术控制星载波束的空间指向，并灵活分配带宽和发射功率，为卫星用户动态分配通信资源[4]，因此BH技术可以用于LEO场景以增加卫星资源利用效率。

BH卫星系统相较于传统卫星系统在资源分配方面能大幅度地提高系统性能和资源分配效率。文献[5]利用遗传算法通过时分复用的方式设计与各时隙业务需求相匹配的BH方案，并展示引入BH技术对多波束卫星系统性能优化的效果。文献[6]提出一种联合资源优化方案，该方案利用迭代算法设计功率控制和波束成形优化策略，不仅能满足系统安全性要求，也大幅度提高资源分配效率。基于BH动态资源分配的思想，文献[7]以最大化高轨卫星用户性能公平性为目标，设计满足信道容量限制下的波束跳变策略，保障了瓶颈用户的通信质量。文献[8,9]均在提出BH系统资源分配的数学模型基础上，利用启发式算法等传统算法设计有效改善卫星前向链路的资源分配方案。为了降低传统优化问题的复杂性，文献[10]在BH资源分配上做了优化和改进，通过将双变量优化问题分解为两个单变量优化问题，有效地解决联合优化问题。文献[11,12]探索一种结合学习和优化的方法，为BH调度提供一种快速、可行和接近最优的解决方案，学习分量能够大大加快BH模式选择和分配的过程，而优化分量能保证解决方案的可行性，提高整体性能。

尽管现有研究在基于BH的资源分配方面已取得较好的成果，但仍然存在3个方面的问题：(1)现有的对BH的研究集中在高轨卫星，缺乏对LEO应用BH技术的可靠研究。(2)大多数基于BH的资源分配只关注系统的吞吐量，而LEO服务时间短暂，对业务的时延敏感，因此优化问题应侧重考虑减小业务时延性能，使优化目标与系统特性相匹配。(3)由于在LEO环境下通信资源和通信需求剧烈变化，传统的BH资源分配算法复杂度高、计算量大，无法直接使用于LEO上。

针对上述问题，本文提出一种基于深度强化学习(Deep Reinforcement Learning, DRL)的低轨卫星跳波束资源分配方案。本文主要的贡献如下：(1)根据LEO场景特点，本文联合星上缓冲信息、业务到达情况和信道状态信息(Channel State Information, CSI)，以最小化卫星上数据包的平均排队和传输时延为目标，建立了可靠的支持BH技术的LEO资源分配模型。(2)针对传统BH图案设计方法无法适应LEO场景的问题，本文考虑动态随机变化的通信资源和通信需求，采用DRL算法，将卫星数据包缓存量、信道状态重构为状态空间，执行小区的波束调度、功率分配决策，根据小区数据包的积累量定义奖励函数，使LEO资源分配过程更加自动化和智能化。(3)为了降低模型的训练成本，使模型更好地适应LEO动态变化的环境，提出了一种新颖的迁移深度强化学习(Transfer Deep Reinforcement Learning, TDRL)模型，将迁移学习(Transfer Learning, TL)和DRL算法结合起来，根据TL的策略迁移特性，使新接入网络的卫星在训练初期拥有少量样本的条件下，也能尽快取得最优资源分配方案，提高了算法的收敛速度。

2 系统模型

如图1所示，本文支持BH的卫星系统包括低轨卫星、网络控制中心、信关站和卫星用户。LEO通过宽波束收集用户信令，以统计不同小区的业务需求，星载处理器通过执行智能算法得出当前时刻波束调度和功率分配决策，完成对地面热点终端的灵活资源分配。新接入LEO网络的用户数据可以通过卫星直接转发给其他用户或透明转发至地面信关站，再由信关站通过地面网络转发数据，从而建立终端之间的通信链路。

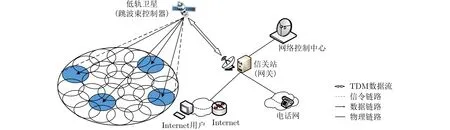
图1 基于跳波束的低轨卫星通信架构

2.1 天线模型

多波束天线辐射特性参考国际电信联盟(International Telecommunication Union, ITU)的建议书ITU-S.672，该建议书给出了卫星单波束天线的辐射特性[13]，LEO天线辐射特性估算参考模型可以设定为

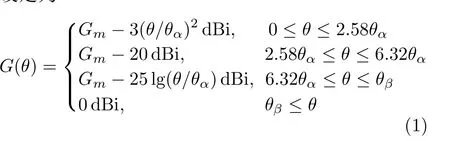
其中，θ为偏轴角，G(θ)为在该偏轴角下的天线增益大小；Gm为天线最大方向性的辐射效率，即天线最大增益，该数值与卫星天线硬件参数有关；θα为 半波束角；θβ为式中第3个等式等于0 dBi时的θ值。LEO卫星多波束模型可设置为由多个拥有该辐射特性的单波束组成，可计算任意时刻卫星对小区的天线增益。

2.2 信道模型

信道矩阵H包含低轨卫星前向链路预算信息和由于无线传播引起的相位旋转[12]。信道矩阵可以表示为

其中，矩阵Z代表信号通过不同传播路径所引发的相位变化，矩阵Z的具体表示为

其中，ϕx为 在区间[−π,π]上服从均匀分布的随机变量。

2.3 前向链路模型

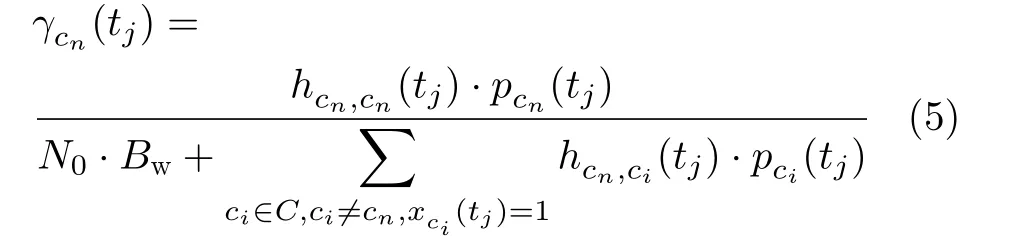
其中，hcn,ci(tj) 表示在时刻tj，覆盖小区cj的波束到小区cn中心的信道增益，该数值可通过查询信道矩阵得到；pci(tj)表 示在时刻tj， 覆盖小区cn的波束发射功率；N0表 示噪声功率谱密度；Bw为波束分配到的全带宽。

在tj时刻，信道条件可以定义为H(tj)={hcn,ci(tj)|cn,ci ∈C}，由于低轨卫星相对于地面移动速度很快，导致信道条件hcn,ci(tj)也随时间快速变化。将当前波束调度时刻与该数据包到达时刻的时间差定义为该数据包的排队时延，传输时延可以通过数据包大小和小区信道容量计算得出。假设小区数据包的到达服从泊松过程，到达率用L(tj)={λcn(tj)|cn ∈C}表示，其中λcn(tj)表 示小区cn在时间段[tj,tj+1]的 数据包到达率，假设数据包pi在tpi时刻到达卫星缓冲区，若波束调度时间间隔足够小，可令tpi ≈tj。F(tj)={fcn(tj)|cn ∈C}表示在tj时刻各小区缓冲区的所有数据包，因此fcn(tj)代表该时刻小区cn缓 冲区数据包集合。定义Tth为数据包最大排队时延，即数据包必须在到达后的Tth时段内被传输，否则以最大时延作为该数据包的排队时延。

假设所有数据包的传输过程遵循先到先服务的原则。卫星缓冲区中的数据包集合F(tj)仅由上一决策时刻的数据包集合F(tj−1)、波束调度决策X(tj−1)、 信道条件H(tj−1)、 功率分配情况P(tj−1)以及数据包到达率L(tj−1)决 定。因此，在tj时刻数据包的集合可以为式(6)表示

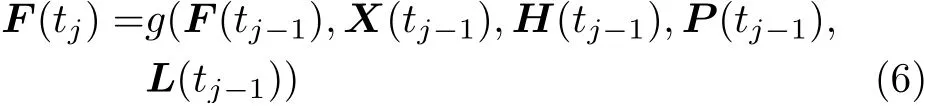
由于当前时刻的数据包集合F(tj)仅与上一时刻F(tj−1)相关，而与之前状态无关，因此，数据包在缓冲区的累计过程具有马尔可夫性。系统的吞吐量也可以根据前后波束调度时刻缓冲区&数据包的数量和当前时刻数据包到达率确定，小区cn在tj−1～tj时间段内的数据包吞吐量表示如式(7)所示

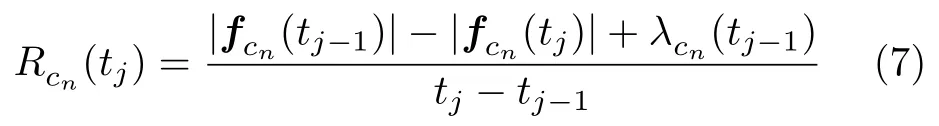
系统的总吞吐量也可以根据所有时刻缓冲区数据包的数量和数据包到达率确定，小区cn在总的时间段内的数据包吞吐量表示如式(8)所示

2.4 优化目标

通过动态的波束调度和功率分配，以最小化一段时间内每个小区数据包的平均时延。因此本文将最小化所有数据包的平均时延作为优化目标，而每个数据包的时延由排队时延和传输时延组成。假定所有数据包的大小相等，且均为Mbit，如式(9)所示，排队时延由包到达时刻与决策时刻的时间差决定，传输时延由数据包大小和该时刻小区的信道容量决定

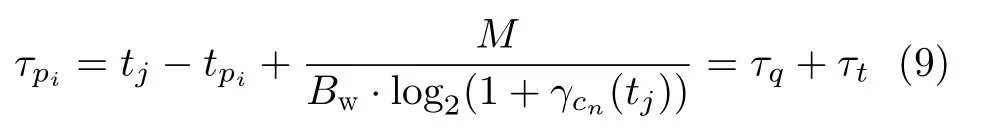
波束调度X(tj)和 功率分配P(tj)作为当前时刻的决策变量，并且决策受到当前时刻其他条件影响，因此决策应该基于数据包集合F(tj−1)、波束调度决策X(tj−1)、 信道条件H(tj−1)、功率分配情况P(tj−1)以 及数据包到达率L(tj−1)。数据包平均时延的最小化数学模型如式(10)所示

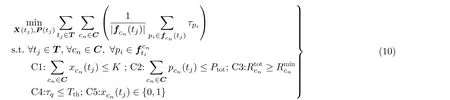
其中，集合T={t1,t2,...,t|T|}表示在卫星覆盖范围内的所有决策时刻的集合，Ptot是星载总功率，表示小区的最小吞吐量要求，Tth表示最大容忍排队时延。C1为最大波束数限制，保证获得波束调度的小区个数不能超过星载有源波束数K；C2为星载资源限制，意味着所有波束的发射功率应在卫星最大星载功率要求之内；C3表示资源分配情况需满足用户服务质量(Quality of Service,QoS)限制，保证小区的总吞吐量不能低于吞吐量阈值，即满足网络的最低服务要求；C4保证卫星缓冲区每个数据包的排队时延要在最大排队时延之内；C5为波束调度状态的二进制变量约束。

3 基于TL-DRL的LEO-BH方案

3.1 算法整体架构

图2为本文设计的基于TL-DRL的LEO-BH系统架构图。系统架构主要包括资源管理系统和LEO前向链路传输网络。首先，LEO宽波束搜集用户信令，统计用户业务量，数据包在即将发往各个小区的卫星缓冲区里排队；其次，监控器负责收集缓冲区队列情况、CSI、星载资源来更新控制器参数；控制器则根据监控器信息执行相应的学习算法；最后，分配器根据控制器的配置参数进行波束动态智能调度和功率分配。

对于该系统架构来说，控制器是可进行优化的模块，包含DRL和TL。DRL通过结合强化学习(Reinforcement Learning, RL)和深度学习(Deep Learning, DL)，完成系统特征的学习并智能地执行资源分配策略[14]。如图2所示，控制器首先利用RL不断与环境进行交互获取样本，再利用DL提取样本特征，完成当前场景到资源分配策略的映射。再利用TL中的策略迁移加速智能体快速寻找最优资源分配策略，优化DRL算法的收敛性能。TL与DRL的结合可以优化系统训练的过程，提高资源分配的效果。

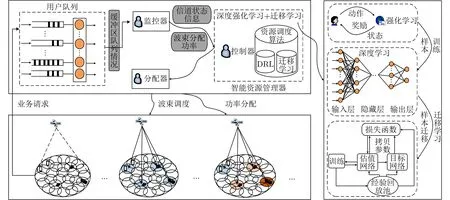
图2 基于TL-DRL的LEO-BH系统架构图

3.2 MDP模型

由以上分析可知，小区缓冲区数据包的累计情况与上一时刻的数据包缓存量、波束调度情况、CSI、功率分配情况和数据包的到达率有关，因此数据包的变化过程具有马尔可夫性，可以建模为马尔可夫决策过程(Markov Decision Process,MDP)，将系统的状态、动作和奖励设定如下。

3.2.1 状态

状态能抽象地表征环境，也是智能体进行波束调度和功率分配的依据。对于特定的时刻，卫星的缓冲区情况F(tj) 和 信道条件H(tj)能直接影响波束调度决策X(tj)和 功率分配动作P(tj)，其中信道条件会影响被服务小区缓冲区数据包的发送速率。在DQN中，若将卫星中所有的小区信道状态、功率分配和缓冲区数据包积累量等信息全部输入到深度神经网络(Deep Neural Network, DNN)中，网络的负载量过大，影响智能体的学习效率，因此需合理定义状态，但又不能遗失重要的环境信息。这里使用文献[15]的状态重构概念进行设计，设计规则和实例如下所示。

由于最大排队时延Tth的限制，因此对于缓冲区fcn(tj)中 的任意一个数据包pi，其到达时间tpi一定处在时间间隔[tj −Tth,tj]中。以当前的决策时刻tj为 起点，往前将Tth时间段分割成大小相等的多个部分，在每一个部分统计该时间段中缓冲包的积累量，该时间段中所有数据包的时延设置为与当前决策时刻tj的时间差。

如图3所示为状态重构实例，“× ”符号表示在某段相邻的决策时刻之间ts到达特定小区的数据包，假定数据包的时延阈值Tth=9·ts，即分成9个部分。W矩阵与D矩阵分别表示数据包的个数与时延，其中W矩阵由不同时间段的F组成，即W(tj)=(F(tj−9),F(tj−8),...,F(tj−1))，相邻时间段的数据包差异反映了各小区数据包到达率、波束调度情况和数据包处理速率等信息，数据包的处理速率又与当前时刻各小区信道条件H(tj)和功率分配情况P(tj) 有 关。因此，重构后的状态W和D既能反映当前环境下的重要状态信息，又大幅度地减少存储状态所需的空间。在该实例中，假设在时隙[tj−4,tj−3]到 达了1个数据包，将要发送给小区c2，则W(tj) 中 的w2,6(tj)为 1，D(tj) 矩 阵中的d2,6(tj)为4。

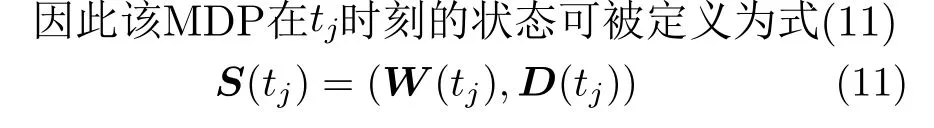
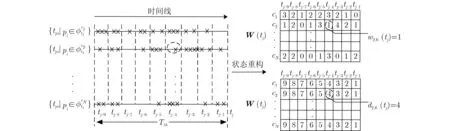
图3 状态重构过程

3.2.2 动作

智能体在观察环境后，通过获得相应的状态S(tj)， 确定在该状态下执行的动作A(tj)。由式(10)定义的时延最小化问题可知，决策组合应该是在满足限制条件C1～C5的一组波束调度向量X(tj)和功率分配向量P(tj)。 所以可将动作空间A(tj)定义为式(12)

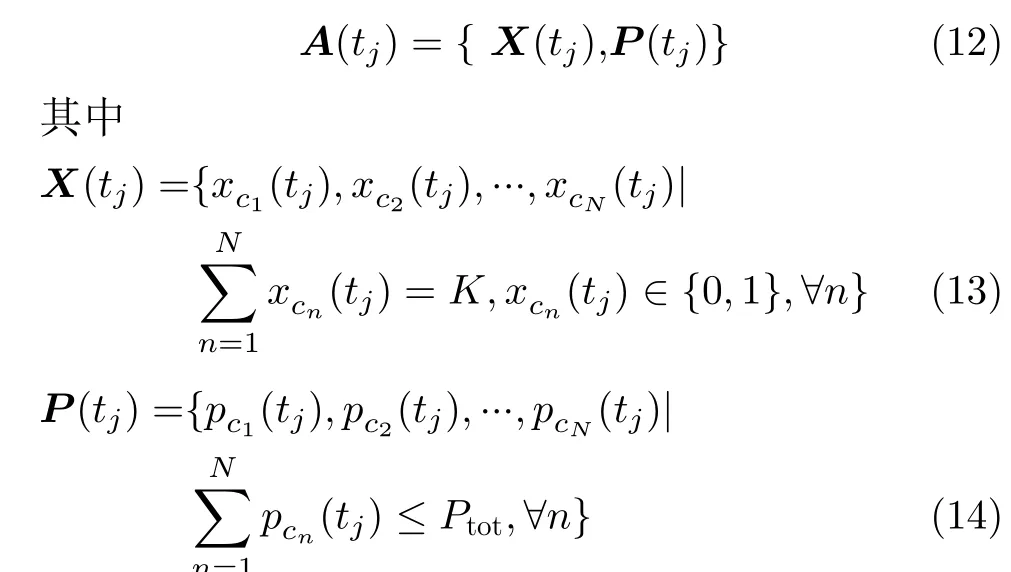
其中，xcn(tj) 代表第n个小区的波束调度情况，pcn(tj)代 表第n个小区能分配到的功率，当小区未获得波束调度权限时，分配到的功率为0，则有

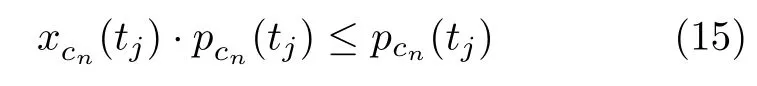
3.2.3 奖励

奖励是MDP中智能体采取动作后的即时反馈。对于式(10)定义的时延最小化问题，根据重构后的状态，可以定义奖励如式(16)所示

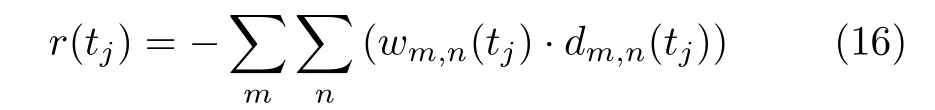
利用当前时刻W矩阵与D矩阵对应元素的乘积之和，该结果能反映卫星缓冲区所有小区的数据包从到达到当前时刻拟发送成功的时间差的和，即所有数据包时延的和，而将其相反数设定为当前时刻奖励，满足奖励的定义要求，即当前的缓冲区数据包积累量越多，数据包的平均时延就越大，获得奖励就越小。

3.2.4 DQN网络结构设计

在DRL中，深度Q网络(Deep Q Network,DQN)是最受关注的算法之一，DQN使用非线性神经网络来近似状态-动作值函数，可以从高维数据中提取特征，并且DQN已广泛应用于智能序贯决策问题中[16]。因此本文将LEO-BH资源分配算法转化成一个深度Q学习过程，通过观察当前网络环境的状态，选择适当的资源分配决策以最小化系统的平均时延。在智能体观测环境并得到状态s(ti)后，立刻通过神经网络得到基于当前状态的决策动作a(ti)， 并 输出 奖励r(ti) 。Q网络 完成 状态s(ti)到 状态-动作值的映射，经验回放池负责存储交互得到的4元组样本，与目标网络和自适应估计 (Adaptive moment estimation, Adam) 优化器共同作用以训练Q网络，提高神经网络的拟合特性。

Q∗(s,a)为 最优的Q值函数，通常情况下以递归方式获取函数 (s(ti),a(ti),r(ti),s(ti+1),a(ti+1))，表示了在当前时刻ti下，系统处于s(ti)状态，采取动作a(ti)并 得到即时奖励r(ti)后，在下一时刻进入状态s(ti+1) 并 有一定概率采取动作a(ti+1) ，Q值函数更新规则如式(18)所示

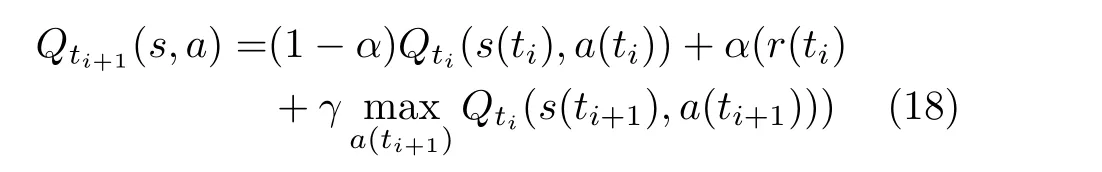
其中，α表示学习率，γ∈[0,1]是折扣因子，折扣因子反映了网络对得到即时奖励的期望程度。本文采用卷积神经网络(Convolutional Neural Networks,CNN)来提取类像素矩阵，拟合Q值函数。为了打破数据间的关联性和缓解非线性网络中Q值函数出现的不稳定问题，利用经验回放池存储获取到的4元组样本，并随机抽取小批量样本数据进行训练，通过存储加采样的方法将数据关联性打破，使训练更加稳定。

如图4所示，深度神经网络由输入层、两层卷积层、3层全连接层和输出层构成。网络的输入是当前时刻状态重构后的时延矩阵和缓冲区数据包滞留矩阵，然后利用CNN提取类像素矩阵的特征，展开并作为全连接层的输入。全连接层拥有“分类器”的功能，能增加系统模型的非线性表达能力。同时，为降低全连接层节点间相互依赖性，防止神经网络出现过拟合现象，在全连接层上采用随机失活策略[17]。

图4 深度神经网络模型

在Q网络训练时需要计算损失函数，损失函数用于评价目标网络和估值网络的差距，引导下一步训练的正确方向，因此损失函数最小也表明算法达到意义上的最优[14]。本文将损失函数定义为

需要通过抽取的4元组样本计算当前估值网络的梯度dw，再使用Adam算法[18]更新参数w

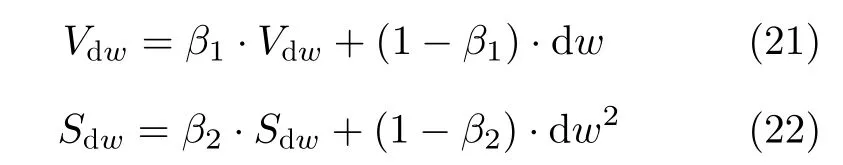
Vdw和Sdw分别表示指数加权平均数和平方数指数加权平均数，为了防止初始化权重更新出现偏差，利用式(23)和式(24)计算该两个平均数的无偏估计，完成对偏差的修正[18]

3.2.5 基于TL-DQN的低轨卫星跳波束方案

LEO虽然可以通过DRL算法采取最佳的资源分配动作，但对于新接入LEO网络的卫星(智能体)来说，虽然与其他卫星覆盖同一片区域，但仍然需要重新与LEO网络环境交互获取新的样本并重新训练DQN模型，以此来得到当前卫星的最优波束调度和功率分配策略。由于低轨卫星对地移动速度过快，较长的训练过程必定减少系统的有效服务时间，降低资源优化性能，且若每一个新接入网络的卫星都需要独立重新训练模型，这无疑增加了系统的训练成本，因此已有关于如何加快DRL算法训练速度的文献研究[19,20]。

其中，ζt=ηt为迁移率，η∈(0,1)为相应的迁移率因子，随着时间的推移和训练次数的增加，迁移率会越来越小。不同取值的迁移率因子会影响系统的迁移率减小速率，即会对迁移学习过程的策略迁移比例。在学习刚开始阶段，源卫星策略(s(ti),a(ti))在整体策略中占主导地位，源卫星策略的存在有较大概率促使系统选择源任务中状s(ti)态的最优动作，然而随着学习时间的推移，源卫星策略对整体策略的影响逐渐变小，这是因为尽管源任务与目标任务相似，但仍然存在差异，例如在不同的时刻，源卫星网络观测到的状态与目标卫星网络观测到的状态一致，但由于卫星处于不同位置，信道条件和各小区需求量也不同，目标卫星应更积极地寻求匹配当前网络环境的最优资源分配策略。因此该TLDQN系统不仅能利用源卫星网络学习到的经验知识，也能逐渐消除外来策略的消极影响。最后，将TL-DQN算法总结在算法1中。

算法1 基于TL-DQN的低轨卫星跳波束方案

4 性能仿真与分析

4.1 参数设置

为了评估模型和算法的有效性，针对LEOBH技术进行了实验仿真。场景设计如下：待服务区域的大小为6670× 6670 km2，并且被划分成49个规模相等的小区，卫星网络包括既定轨道和一个拥有7个点波束的LEO卫星组成。仿真场景的其余物理参数参考铱星系统[21]，其中，数据包大小均值设置为M=50 kbit，数据包到达服从泊松分布且到达率(包/s)范围为：λcn(t)∈[1,21]。仿真场景具体参数设置如表1所示。

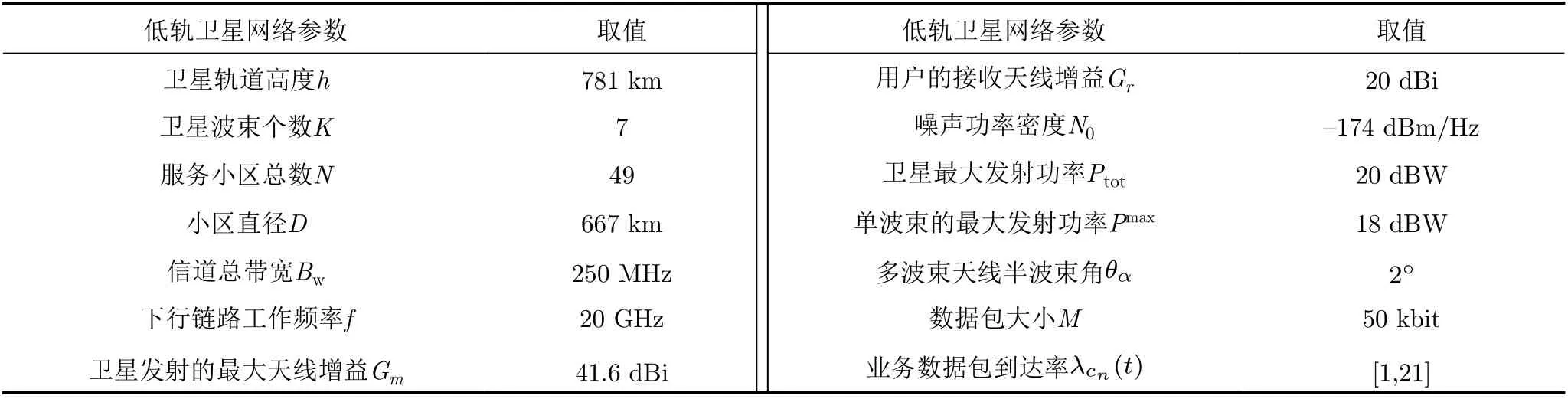
表1 低轨卫星场景设置参数

本文的算法采用TL-DQN算法来解决多波束低轨卫星网络中波束调度和功率分配问题，因此还需要对神经网络的参数进行训练，表2即TL-DQN算法的参数设置。经验回放池存储神经网络的样本来源于智能体与环境交互所感知到的数据，若容量过小，则会丢弃部分经验样本以至于训练不稳定，本文将经验池的容量设置为5000。当前Q网络每次进行训练时，会随机获取经验池中的10组数据进行训练，并且每100步更新目标Q网络的参数值。由于Adam的系统时延收敛值明显低于其他优化器且震荡幅度更小，因此本文选择Adam优化器对参数向量进行改进。神经网络的探索概率ε代表智能体随机选取动作的概率，探索概率过大或过小都不利于网络的训练，因此本文使用动态的探索概率[22]，其表达式满足：

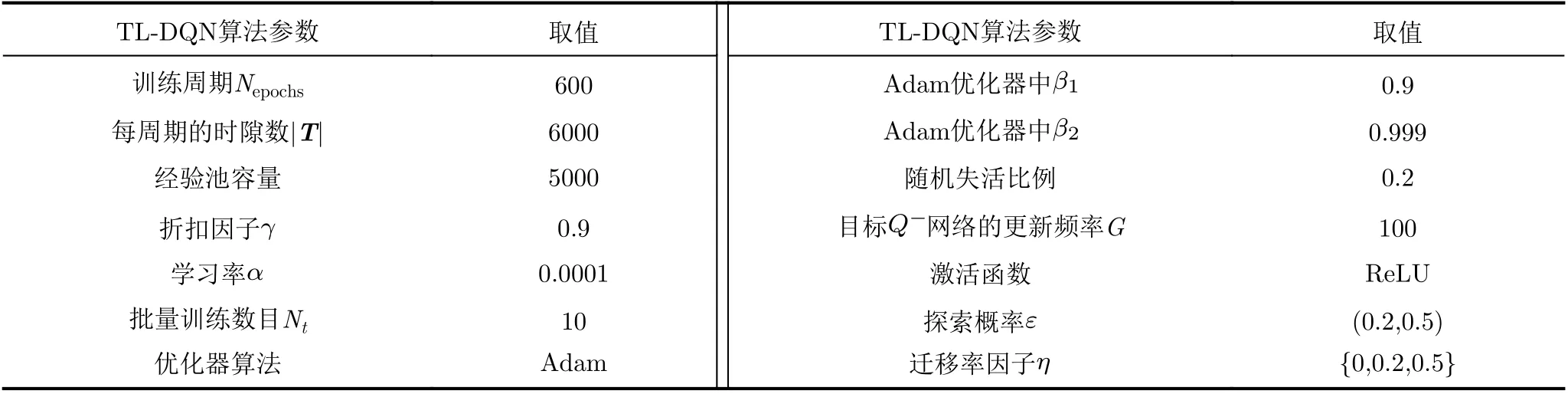
表2 TL-DQN算法参数设置

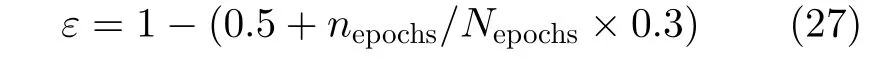
为了验证加入迁移学习后的DQN算法在收敛系统时延和收敛速度的性能优越性，需要设置不同迁移率，迁移率因子满足η ∈{0,0.2,0.5}，其中η=0时表示未使用迁移学习。

4.2 性能分析

4.2.1 算法收敛性能

图5展示了不同的迁移率因子收敛系统平均队列时延的结果。由该结果可以看出，TL-DQN算法的收敛速率优于DQN算法，同时，TL-DQN算法的稳定平均队列时延均低于DQN算法。随着迁移率因子的增大，系统受到迁移过程的影响程度增大，TL-DQN算法的收敛速度越快，且最终收敛的效果也越好。当迁移率因子η=0.5时，TL-DQN算法所达到的系统的平均队列时延相较于DQN算法降低了约13.23%。

4.2.2 系统性能

为了更好地体现本文基于TL-DQN算法的低轨卫星跳波束方案在各个小区拥有不同业务需求量的条件下时延和吞吐量上的优越性，本文将所提算法与轮询调度算法(Round-Robin Scheduling, RRS)和最大队列优先算法(Max Queue First, MQF)进行了比较。图6展示了在不同小区业务需求规律变化的情况下，不同算法的时隙分配个数、业务处理情况和包的平均时延。图6(a)描述了不同算法在低轨卫星服务用户的6000个时隙内，不同小区的时隙获得情况，其中RRS算法小区间的时隙分配差异不大，MQF算法则会根据当前决策时刻的小区队列情况分配时隙，TL-DQN算法根据当前的队列情况，信道状态和功率分配情况构建状态矩阵，通过神经网络得到小区的波束调度决策和功率分配情况，决定了小区获得的时隙情况。图6(b)描述了不同算法的业务处理情况，即小区吞吐率和QoS的满足情况，可以看出TL-DQN算法在满足小区QoS的前提下，大幅度地提高了热点区域的业务处理性能，实现了资源的有效利用，TL-DQN算法、RRS算法和MQF算法的QoS满足率为100%, 38.8%,71.4%，平均业务处理量分别超出QoS需求97.1%,0.4%, 27.6%。图6(c)展示了不同算法下不同小区的包平均时延，结果表示TL-DQN算法小区的总体包时延明显低于RRS算法和MQF算法，由于在RRS算法和MQF算法中，存在需求量较低的小区获得更多的调度时隙，因此可以解释TL-DQN算法有少量小区的包平均时延较高，但总体来说，TL-DQN各个小区的平均时延相较于RRS算法和MQF算法降低了28.15%和19.56%。

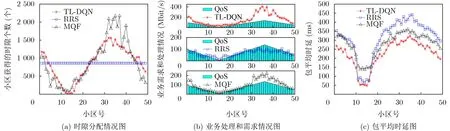
图6 小区需求规律变化下系统性能展示图

为了更直观地衡量TL-DQN算法的优化程度，现研究不同业务到达率对系统吞吐量、包平均时延的影响。图7描述了在业务非均匀分布的情况下，系统吞吐量和包平均时延与系统平均业务到达率的关系。可以看出，随着系统业务到达率的增大，待处理的数据包增多，系统的总吞吐量会增大，且由于队列的积累量变大，包平均时延也会变大。进一步地，可以看出TL-DQN算法的系统总吞吐量和包平均时延均优于RRS算法和MQF算法，且在业务到达率逐渐增大的情况下，性能恶化速度较慢。

图7 系统性能与业务到达率关系图

5 结束语

本文研究了低轨卫星波束调度和资源分配问题，通过将以最小化平均数据包时延为优化目标的随机优化问题转化为深度强化学习过程。本算法联合星上缓冲信息、业务到达情况和CSI，将各个小区数据包缓存情况、平均时延作为状态空间，协助低轨卫星快速、智能地执行小区波束调度、功率分配动作。进一步地，利用TL的算法特点，设置策略更新方式，加快DQN算法的收敛过程并提高收敛效果。仿真结果表明，TL-DQN算法在满足最低QoS需求的情况下能够实现包平均时延最小化，也有效地提高了系统的吞吐量。