复杂地形环境下基于GAMP-STAP的低空风切变风速估计方法

李 海 谢瑞杰 谢伶莉 孟凡旺

①(中国民航大学天津市智能信号与图像处理重点实验室 天津 300300)

②(中国航空工业集团公司雷华电子技术研究所 无锡 214063)

1 引言

低空风切变是影响民航运输安全和效率的危险天气之一，其具有持续时间短、作用距离小、瞬时强度大、变化多端、危害性强等典型特征[1]。当飞机在起降过程遭遇风切变时，由于此时飞行高度低，飞行员缺乏足够的时间和空间调整飞机姿态，从而导致飞行事故的发生，因而低空风切变检测和预警成为民航安全领域的重要课题。而风切变风速估计是风切变检测和预警的基础，因此，准确估计风速至关重要。近年来，我国大力推进机场建设，中西部高原地区需建设的机场越来越多[2]。建设在高原地区的机场，由于海拔较高，机场接近大气层的中层，乱流多，风场变化大，低空风切变明显，同时复杂的地形环境增大风切变的探测难度，严重威胁航空安全。机载气象雷达作为飞行气象环境实时探测的重要手段，探测低空风切变时，处于下视工作模式，风切变目标淹没在强地杂波中，因此首先需要杂波抑制然后估计风速。而高原机场复杂的地形环境，增大了地杂波的非均匀性，也会使风切变的类型变为更加复杂的非对称型风切变，进一步增大杂波抑制风速估计的难度，从而影响风切变检测的可靠性。

对于相控阵体制的机载气象雷达，空时自适应处理(Space-Time Adaptive Processing, STAP)技术[3]可以在空时联合域中获得更好的地杂波抑制效果。STAP技术最优权矢量依赖于杂波协方差矩阵(Clutter Covariance Catrix, CCM)的准确估计[4]。但是传统STAP技术要求独立同分布(Independent Identically Distributed, IID)样本达到系统自由度(Degree Of Freedom, DOF) 2倍或以上[5]才能准确的估计杂波协方差矩阵，以构造STAP滤波器。而在复杂地形环境下，由于地杂波的非均匀性和IID样本数严重匮乏，无法满足该条件。因此，探讨复杂地形环境情况下的低空风切变风速估计具有十分重要的意义。

目前，对于非均匀环境下的STAP目标检测技术主要有非均匀STAP[6]、降秩STAP[7]、降维STAP[8]、知识辅助STAP(Knowledge-Assisted STAP, KA-STAP)[9,10]、稀疏STAP[11]。单样本直接数据域(Direct Data Domain, DDD)非均匀STAP方法有效地消除了杂波非均匀的影响，但在空时域滑窗得到IID样本会存在孔径损失问题且受空域和时域自由度的影响较大，影响杂波抑制的性能。对角加载样本协方差矩阵求逆(L o a d e d Sampling Covariance Matrix Inversion, LSMI)的降秩STAP和多通道联合自适应处理(Multiple Doppler Channels Joint Adaptive Processing, MCAP)的降维STAP方法都减少了杂波协方差矩阵估计的IID样本数，但是，所需样本的数量仍然较多。知识辅助STAP (Knowledge-Assisted STAP,KA-STAP)方法利用地面杂波先验信息，减少估计杂波协方差矩阵的样本数需求，能够很好地估计出风速。然而复杂环境的无法预料可能导致IID训练样本严重不足，并且无法获取外界地理环境知识的辅助，无法满足KA-STAP的条件。稀疏STAP方法利用杂波空时功率谱的稀疏特性可在极少样本情况下高精度地恢复出杂波协方差矩阵，因而利用稀疏恢复STAP可提高复杂非均匀地形环境下杂波抑制与目标检测性能。然而传统稀疏恢复类算法[12]，如加权二范数最小化(FOCal Underdetermined System Solver, FOCUSS)算法[13]、正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法[14]等方法面临计算复杂度高且正则化参数设置难的问题；稀疏贝叶斯学习方法[15](Sparse Bayesian Learning,SBL)，无须设置正则化参数，性能稳健，但是SBL每次迭代都伴随着矩阵逆运算，因此随着问题维度的增加，将导致很高的计算量，从而无法进行实时处理。

针对上述稀疏恢复算法参数设置困难和运算量大的不足，本文提出了一种基于广义近似消息传递(Generalized Approximate Message Passing,GAMP)STAP的方法。GAMP是近似消息传递算法[16]的推广，稀疏恢复问题中，GAMP能够有效近似计算边缘后验分布，将其运用于稀疏恢复算法，可以减少算法复杂度[17]。因此本文利用GAMP算法开发低复杂度稀疏贝叶斯学习算法，该方法采用高斯混合稀疏先验模型，将GAMP嵌入到EM(Expectation-Maximization)框架中，通过GAMP迭代得到稀疏系数矢量后验分布的近似[18]。从而规避了传统SBL算法中矩阵求逆运算，显著地降低了运算时间。此外，引入了飞机飞行参数和雷达系统参数辅助GAMP-STAP中空时导向字典的构造，以避免网格失配和字典间相关性太强进而导致稀疏恢复算法性能下降的问题。该方法实现了复杂地形环境下杂波协方差矩阵的准确估计，有效地提高了STAP抑制杂波估计风速的性能。

2 机载气象雷达回波信号模型

机载雷达前视阵由N元均匀线阵组成，其探测低空风切变时如图1，机载平台高度为H，速度为V，θ0,φl分别表示风切变目标的方位角和俯仰角，θ和φ分别表示地面散射体的方位角和俯仰角。相干脉冲数为K，脉冲重复频率为fr，相干处理时间有L个距离单元，第l(1,2,...,L)个距离单元空时快拍数据yl表示为

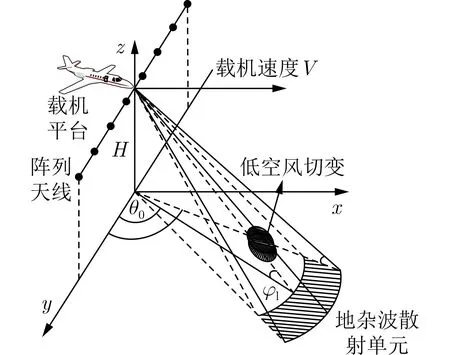
图1 机载气象雷达视探测低空风切变几何模型

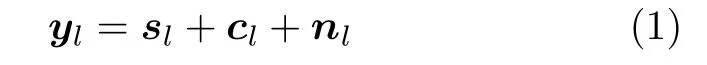
其中，nl为 高斯白噪声，sl为 第l个距离单元的风切变信号，cl为非均匀地杂波信号，本文采用Ward模型融合DEM和NLCD数据仿真高保真地杂波信号[19]。

sl表示为

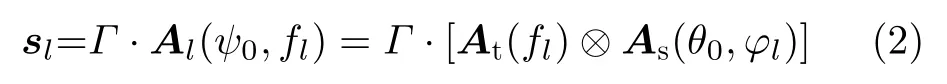
其中，Γ为风切变信号复幅度，A(ψ0，fl)为风切变信号空时导向矢量，ψ0为风切变信号空间锥角，cosψ0=cosθ0cosφl，fl(fl ∈[−1,1])为风切变信号归一化多普勒频率，As(θ0，ϕl)、At(fl)分别为风切变信号的空域导向矢量和时域导向矢量[20]

3 基于GAMP-STAP的低空风切变风速估计方法

基于GAMP-STAP的低空风切变风速估计方法结合飞机飞行参数和雷达系统参数，利用杂波脊的先验信息构造空时导向字典；然后在空时导向字典上通过GAMP算法迭代获得杂波幅度计算协方差矩阵；进而设计STAP滤波器实现杂波抑制并估计风速，该方法原理框图如图2所示。

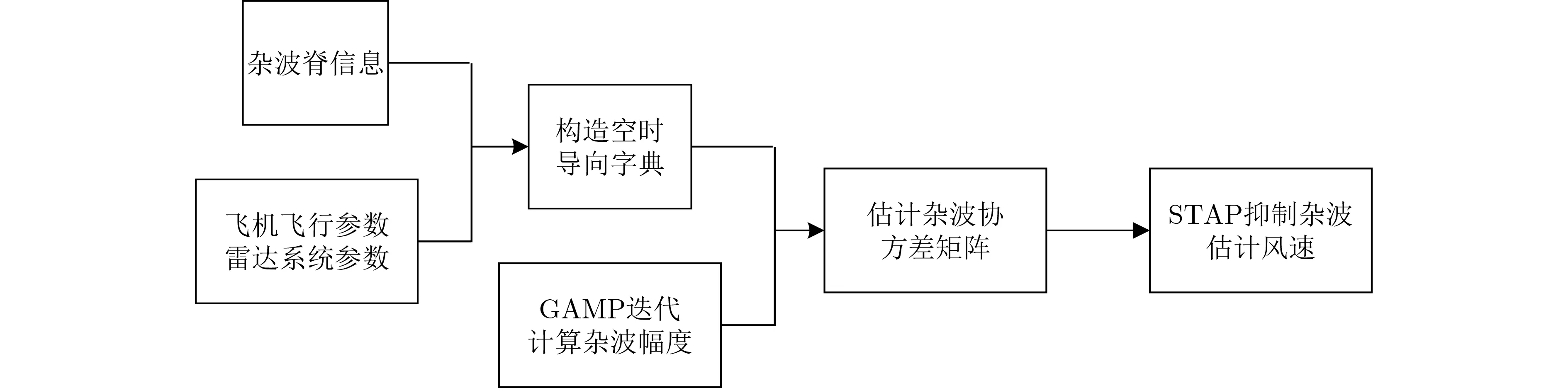
图2 GAMP-STAP的低空风切变风速估计原理框图

3.1 空时导向字典构造

机载雷达回波信号由不同方向和不同多普勒频率的回波信号叠加而成。如果将空域和多普勒频率分别均分成Ns=ρsN和Nt=ρtK个网格点(ρs，ρt分别表示离散化系数)，整个空时平面被分成J=Ns×Nt个 点，则距离单元l的回波接收数据稀疏模型[22]可以表示为

目前，稀疏恢复STAP方法中字典主要是根据以上均匀划分处理得到，虽然简单易处理，但是存在网格失配问题。因此本文利用杂波脊的先验信息构造空时导向字典[23]可以减小上述影响。

机载前视阵雷达下杂波的归一化多普勒频率与归一化空间频率关系为

3.2 基于GAMP估计杂波协方差矩阵

基于GAMP算法估计杂波协方差矩阵，首先建立GAMP模型，给出稀疏系数矢量的稀疏先验分布，通过GAMP迭代得到稀疏系数矢量的近似真实后验分布，然后利用EM算法更新超参数，最后获得空时导向字典每个网格点的杂波幅度以计算杂波协方差矩阵。

(1) GAMP模型。GAMP算法中采用通用的D项高斯混合(GM)[23]对待估计的稀疏向量x=[x1,x2,...,xg,...,xG]T建模，其先验分布为式(8)所示的复高斯分布：

根据文献[24]，GAMP算法中有两个重要的近似：

一是使用输出端的边缘后验分布来近似真正的边缘后验分布p(zw|y;q)( 其中w=1,2,...,W)

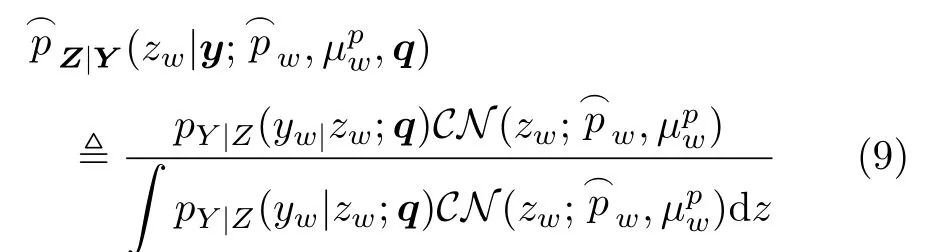
其中，pY|Z(yw|zw;q)是 输出端的似然函数，zw≜aTwx表示无噪声输出量，aTw表 示字典A的 第w行 ，͡pw和µzw是GAMP算法的迭代中间变量。

另一个是在输入端用下式来近似真实的后验分布pX|Y(xg|y;q)( 其中g=1,2,...,G)

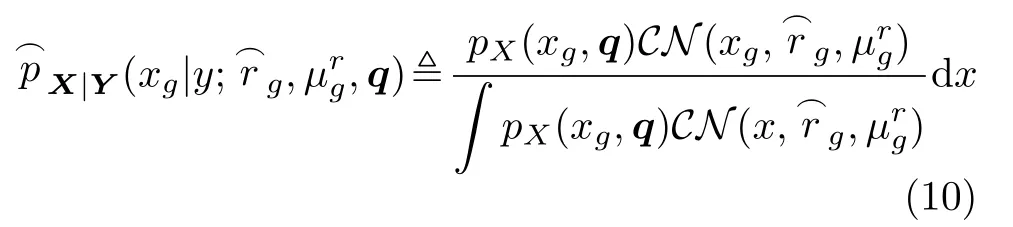
此时，根据贝叶斯准则，结合稀疏向量先验式(8)和后验分布式(10)，得到稀疏向量的边缘分布，根据高斯分布乘积法则可得到pX|Y(xg|y;q)服从高斯分布，具体式(11)所示。

GAMP算法估计待重建信号的过程可用图3的因子图来表示，其中输出变量xg(红色圆圈表示)代表空时平面上第g(g=1,2,...,G)个网格点复幅度，即所求的稀疏向量；输出变量yw(蓝色方框表示)代表接收数据向量分量，即雷达回波数据IID样本；首先是红色的小箭头，表示信息传递方向，代表的是xg传 递给yw节 点的信息，即xg结合自身先验概率更新的后验概率；蓝色的小箭头表示yw传 递给xg节点的信息，即对xg的后验概率的更新推断；物理意义即在已知雷达接收数据、稀疏字典以及输入后验分布、输出端的先验分布基础上，通过输入端和输出端的不停迭代直到算法收敛[24]，得到基于MMSE准则下xg的估计。对于GAMP算法，最重要的是尺度函数的求解。

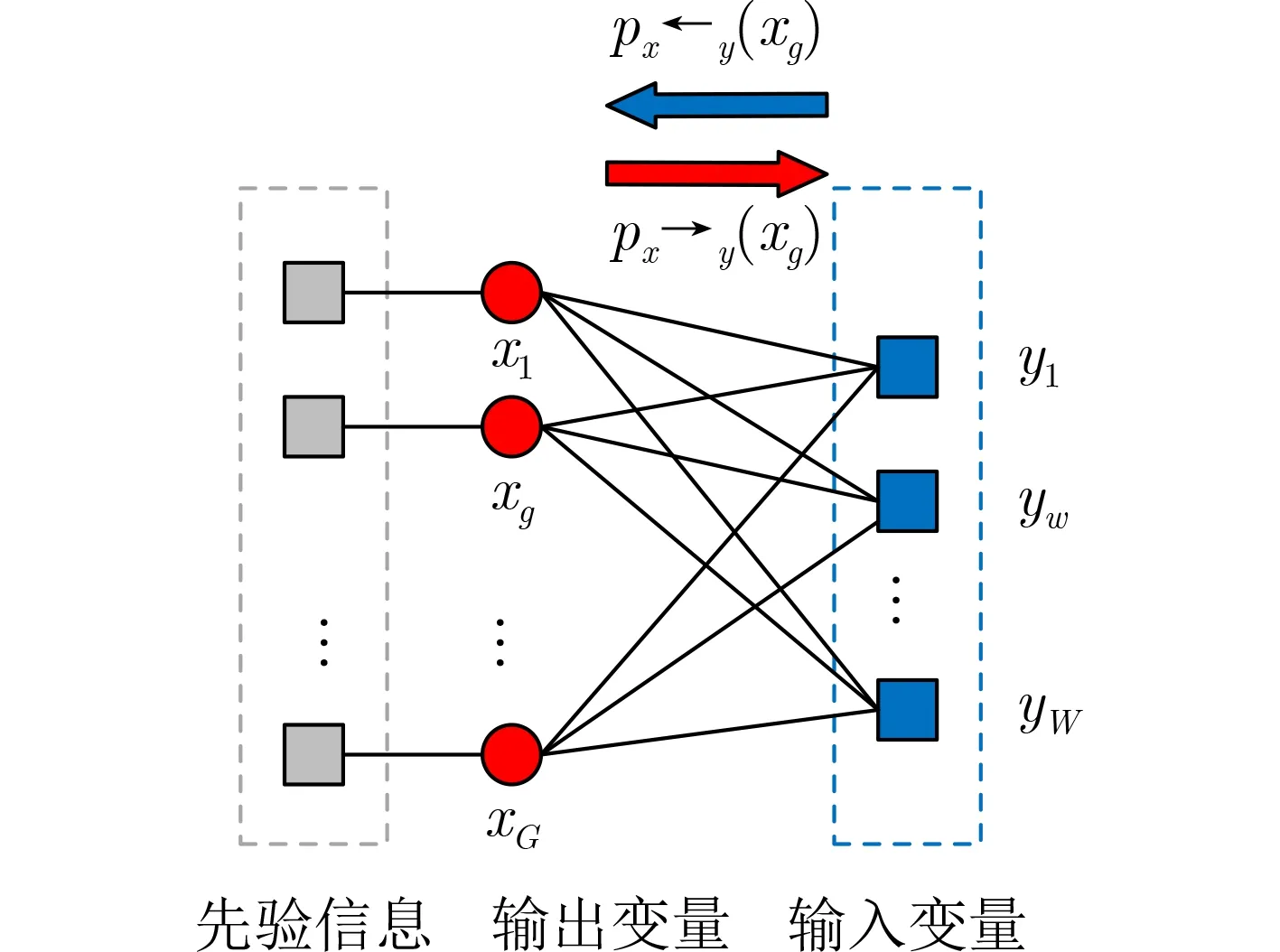
图3 GAMP算法估计待重建信号因子图

3.3 风速估计

对雷达回波信号进行滤波处理后，当前待检测距离单元的地杂波被抑制，且该距离单元风场目标的多普勒频率可由下式搜索得到

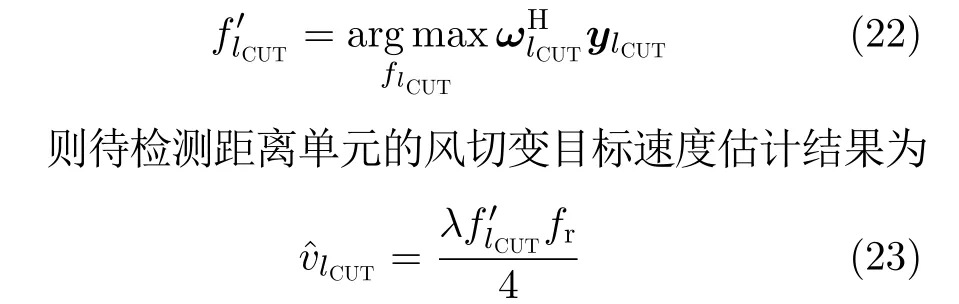
4 方法流程

本文提出的基于GAMP-STAP的风切变风速估计方法流程如图4所示。

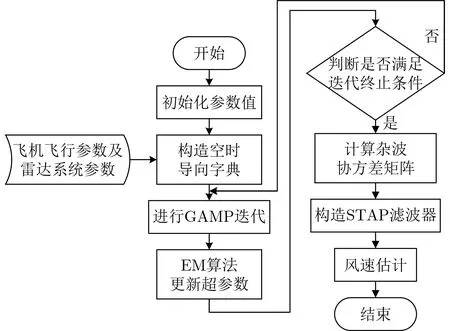
图4 基于GAMP-STAP的风切变风速估计方法流程图

步骤总结如下：

步骤1 初始化参数值；

步骤2 结合飞机飞行参数和雷达系统参数构造空时导向字典；

步骤3 给出稀疏系数向量的稀疏先验模型，并利用GAMP算法进行迭代，求解稀疏系数向量；

步骤4 将GAMP算法得到的稀疏系数向量和中间量按照式(16)、式(17)EM更新规则，进行迭代更新，并判断是否达到迭代停止条件，若无，则重复步骤3，若有，则输出最终的稀疏系数向量估计值；

步骤5 计算杂波协方差矩阵；构建STAP滤波器，进行杂波抑制以及低空风切变风速估计。

5 实验结果分析

5.1 仿真条件描述

本文中，设定非对称低空风切变场的入射倾角为20°，入口速度为40 m/s ，风场范围为飞机前方8.5～16.5 km，雷达系统仿真参数如表1所示。

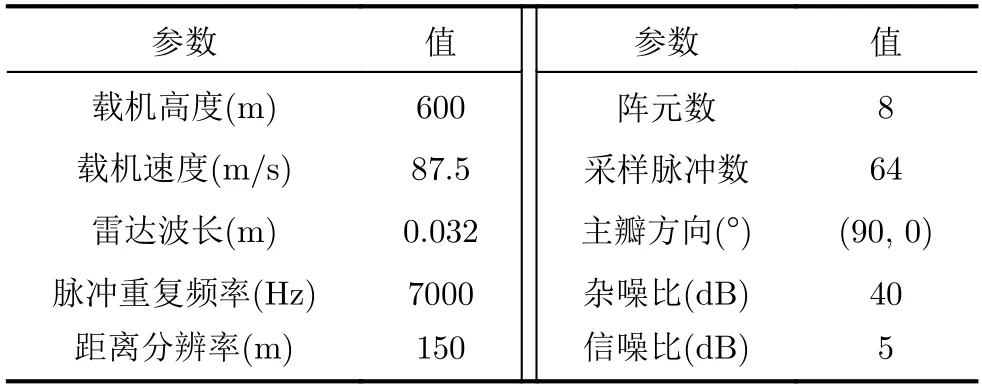
表1 雷达系统仿真参数

5.2 仿真结果分析

图5展示了地杂波的距离多普勒图，图5(a)和图5(b)分别为均匀环境和复杂地形环境下地杂波距离多普勒图，从图中可看出，复杂地形环境下杂波的非均匀性和非平稳性现象十分明显，表现了高原地区回波数据特征。

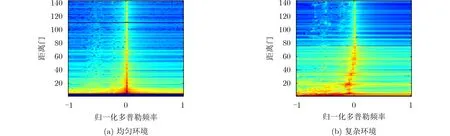
图5 地杂波距离多普勒图

图6为前视阵机载气象雷达回波信号空时2维谱，杂波谱呈半圆形分布，体现了杂波谱前视阵结构的空时耦合特性，低空风切变信号在空时域呈现为有一定的展宽的一条“窄带”，并且从图中可以看出地杂波信号的回波功率远大于低空风切变信号的回波功率，风切变回波多普勒信息淹没在地杂波的多普勒信息中，严重影响风切变速度估计与检测。

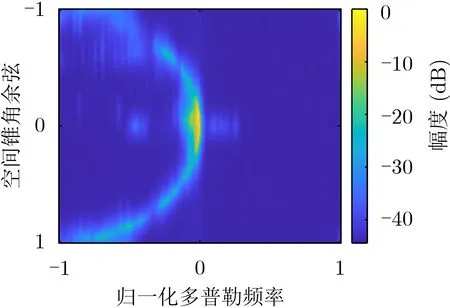
图6 机载气象雷达回波空时2维谱

图7为本文基于GAMP算法对第60号距离单元杂波功率谱的恢复结果，空间尺度ρs=10,ρt=8，当采用传统的空时字典时，算法性能不稳定并不能保证每次算法都能收敛；当网格划分致密导致字典的列相关性太强，算法性能损失时，杂波谱恢复结果如图7(a)所示，图7(b)为在相同的空间尺度下引入杂波脊先验信息构造的字典情况下恢复的结果，能够保证算法每次都能收敛，得到较好的信号恢复结果。同时说明本文算法利用8个训练样本能够较好地恢复杂波的功率谱。

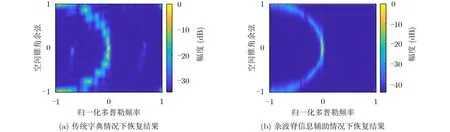
图7 GAMP算法恢复的杂波功率谱

图8为GAMP-STAP方法与传统STAP, KASTAP, SBL-STAP的风速估计结果对比图，可以看出本文方法在复杂地形环境下能够准确估计风速，而传统STAP, KA-STAP方法性能很差。相较于SBL-STAP方法，本文方法准确度更高一些，并且运算量和运算速度得到很大提升。

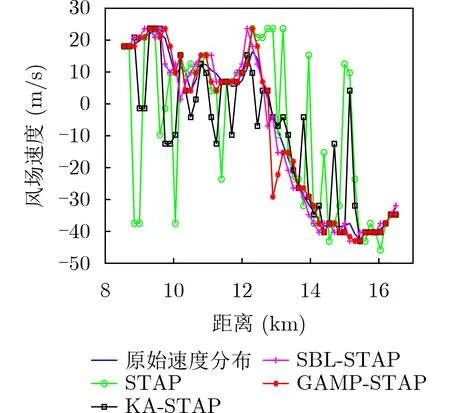
图8 不同方法风速估计结果对比

表2为本文方法与传统SBL-STAP方法完成单个距离门风速估计的运行时间对比，其中W=NK为接收信号维度，其中N为阵元数，K为脉冲数；G为空时2维平面的离散点数。计算复杂度为1次迭代复杂度，运行时间为估计1个距离单元风速的时间。取同样的空间分辨尺度(ρs=10,ρt=8)，可以看出由于传统SBL-STAP方法涉及矩阵逆运算，计算复杂度高，运行时间慢，而本文方法在贝叶斯框架下使用GAMP算法来迭代估计杂波幅度，计算过程仅涉及乘法运算，大大减少了运行时间。

表2 算法运行时间对比

6 结束语

本文针对复杂地形环境造成的非均匀杂波情况和IID样本数不足问题，提出一种基于GAMP-STAP的风切变风速估计方法。在稀疏背景下，该方法首先利用杂波脊的先验信息构造空时导向字典，接着用GAMP算法迭代计算稀疏系数向量，并用EM算法更新学习超参数集合，最后得到杂波协方差矩阵的估计结果，构造STAP滤波器抑制杂波实现风切变风速的准确估计。实验仿真结果表明该方法能使用少量IID样本实现风速较准确估计，并且算法计算复杂度低，较于传统SBL-STAP大大减小了运行时间，对于复杂地形环境下的低空风切变风速估计具有更好的实用价值。