数学推广:模式、方法及教育价值
2023-02-28吉智深
吉智深
(南通师范高等专科学校, 江苏 南通 226500)
在《小学数学基础理论》这门课程的考试中,笔者出了这样一道题:你能够推广“连续两个自然数的乘积能够被2整除”这个结论吗?这道题就是想考考师范生对数学推广的认识与掌握,本以为比较简单的题目,但答题情况很不理想,许多学生都空在那里,没有任何想法。考试结束后,问学生做不出的原因,不少学生说不知道什么是推广。推广可是数学研究中极重要的手段之一,数学专业的师范生还有一些人不知道什么是推广、更不知道如何推广,有点说不过去。由此可以看出把学会数学推广纳入数学教师专业知识是非常必要的,对广大小学数学老师的专业知识也是有益的补充,只有教师理解了数学推广,学会了数学推广,才能有意识引导学生去探究、去思考、去创新,才能在培养创新人才的道路上向前再踏实地迈一步。
一、数学推广的模式
“数学推广是指在一定范围内或一定层次上对数学概念、定理、法则进行拓展,使之在更大范围或更高层次上成立,此外,也指对条件、结论进行结构分析以后,进行适当变化,使得到的新命题为真。”[1]数学家们一致认为“数学推广本身就是数学研究的重要方法”。比如,米山国藏就曾指出:“每当我发现一个新定理,就立即集中力量从各方面考查这定理能不能将它一般化、能不能推广,从而一步一步进行研究工作?”[2]既然推广在数学研究中的地位如此之高,那数学推广的模式是什么?这是我们必须首先了解的问题。
模式1:空间高维化
数学习惯上把直线叫作一维空间,平面叫作二维空间,立体几何中所在的“空间”叫作三维空间。除此之外,“维数”还泛指未知数与变量的个数、方程与不等式的次数、行列式与数表的阶数等。数学家喜欢将数学问题从低维推广到高维,如平面几何的勾股定理能否推广到立体几何?一元一次方程和一元二次方程都有公式解,那么推广到一元三次方程、一元四次方程、……都有公式解吗?大数学家费马通过推广毕达哥拉斯方程:x2+y2=z2,提出了举世闻名的费马猜想,即“xn+yn=zn是否有整数解”。前面的试题“‘推广连续两个自然数的乘积能够被2整除’这个结论”也属于这方面的推广,从未知数的两个推广到三个,四个,……。这方面的例子比较多,也是最容易被我们忽视的一点。
模式2:范围扩大化
数学的概念、定义与定理等随着数学研究的范围不断扩大,如何把原有的这些数学知识与方法推广到更大的范围内适用呢?这是数学推广常用的一种模式,一些数学结论在大的范围是否适用?这方面小学数学最典型的例子是:加法的交换律与结合律推广到乘法是否成立?加法与乘法的运算律在自然数范围内研究的,但这些运算律从自然数推广到分数、小数范围内是否仍然是成立的呢?看到sin(α+β),能否也可以利用乘法分配律推广得到sin(α+β)=sinα+sinβ?高中数学把0°~360°角推广到任意角,随着角的范围扩大与研究的需要,有必要将锐角三角函数推广到任意角的三角函数,如何推广则将是摆在学生面前的一个好问题。
模式3:常数字母化
常数字母化就是把对于几个特殊常数(情况)成立的数学公式、规律推广到对于所有数字(情况)都成立的一种模式。如乘法分配律,根据苏教版教材情境,得到解决问题的两种方法:(6+4)×24=240(根)与6×24+4×24=240(根),从而有(6+4)×24=6×24+4×24,教材引导学生再写出几个这样的等式,最后用字母表示该规律得到:(a+b)×c=a×c+b×c。
高中数学也经常有这样从数字字母化的推广,如,一个口袋内装有大小不同的6个白球和1个红球,请问:
(1)从口袋内取出4个球,共有多少种取法?
(2)从口袋内取出4个球,使其中含有1红球,有多少种取法?
(3)从口袋内取出4个球,使其中不含红球,有多少种取法?
模式4:状态一般化

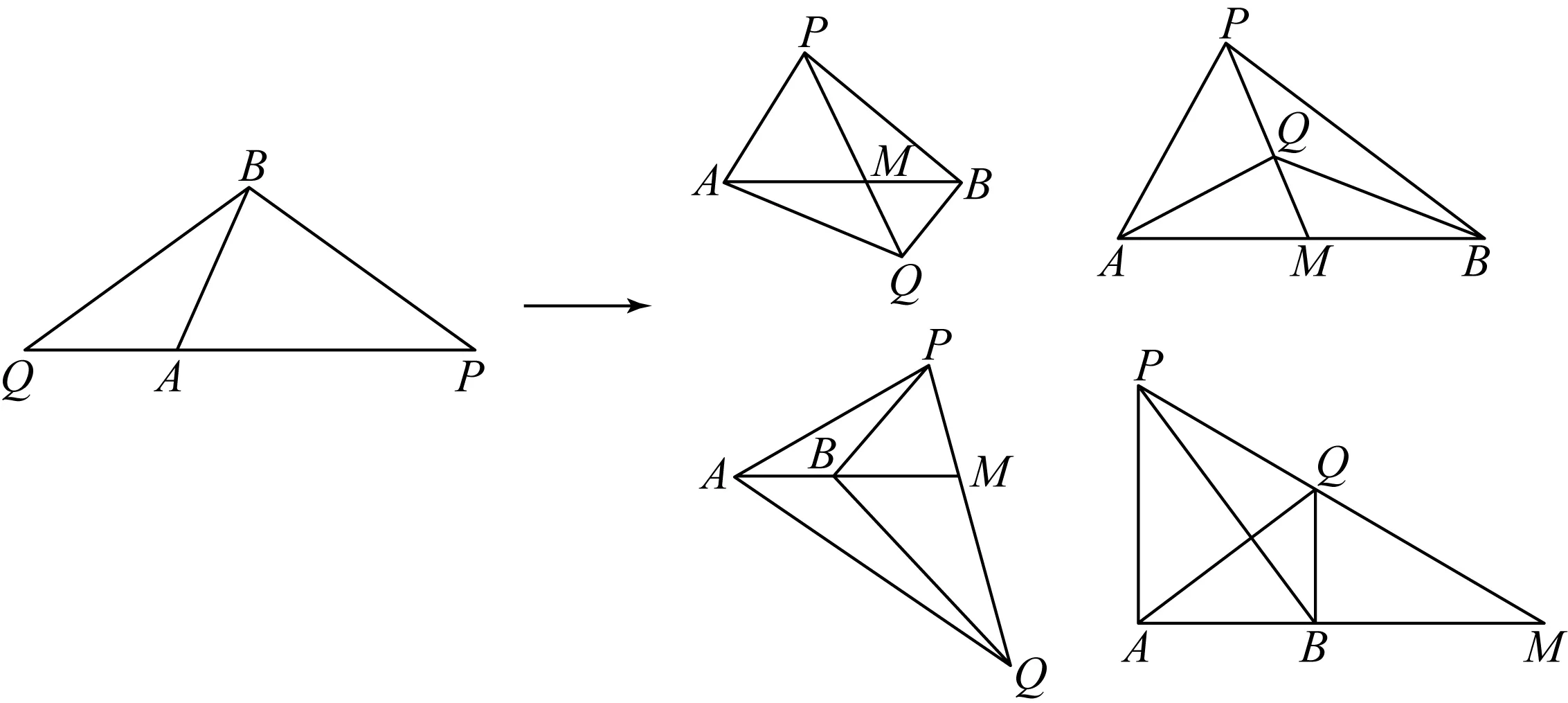
图1 图2


图3
模式5:思想迁移化
前面四种推广模式基本上都是数学命题、规律、定理和公式等在数学学科内深入推广,事实上,数学思想方法的推广更为重要,如果推广的思路被证明是正确的,那将会产生新的解法思路与数学理论。数学思想方法的一个源头就是欧几里得《几何原本》,它从大量现实中提炼出了23个定义、5个公理和5个公设的真理,由这些真理出发演绎出约500个定理。几千年以后,算术上也有了类似的理论,那就是皮亚诺算术公理,只不过这个自然数的公理体系中只有5个公理。另外,第5个公理不得不提,我们称其为 “归纳公理”,又称为“递归公理”,用此公理就可以证明有关对于任意自然数均成立的命题,这种方法被人们称为数学归纳法,后来数学归纳法有了进一步推广与变形,出现了第二数学归纳法、倒推数学归纳法,等等。数学思想方法的另一个源头就是《九章算术》,它主要通过“观察—分析—归纳—概括”的过程,总结出抽象的结论,对抽象理论辅以一定数量的实际问题来加深理解,这种思想方法就是推广的一般过程,另外推广与应用是紧密联系的,应用就体现了抽象理论的推广价值。
二、数学推广的方法
前面介绍的数学推广的5种模式,我们仔细分析与思考后不难发现,数学推广的主要思想方法是:归纳法与类比法,除了这两种方法以外还有探索性演绎与信息交合法。
(一)归纳推理法
模式1与模式3所体现的思想方法就是归纳法,当然这里主要用不完全归纳法,即通过对部分对象的研究,归纳出共性特征,最后提出推广的猜想命题。其思路是“举例—观察—归纳—猜想”,当然,这种推广的命题仅仅是猜想,它是正确或错误,还要经过举反例或严格证明来断定。用归纳法进行数学推广关键要帮助学生树立归纳的意识,要让学生理解把数学概念、命题与思想等进行推广的目的与意义。
如何把直角三角形的边之间满足的勾股定理推广到一般三角形?
如图4,直角三角形ABC的直角C变小时,边c也变小,直角C变大时,边c也变大,可以得出边c的长度与三角形边a、b以及它们的夹角C,而且是与夹角C的余弦函数有关,可以猜测:c2=a2+b2±( )cosC,当C是钝角时,cosC是负的,而边c变大,所以括号前面应该是“-”,而括号里面应该有ab这一项,也就是c2=a2+b2-(ab)cosC,我们再用一个特例检验,当a=b时,三角形ABC是等边三角形,a=b=c,所以前面的猜想是不正确的,ab的前面还应该有一个系数2,最后得出猜想:c2=a2+b2-2abcosC。
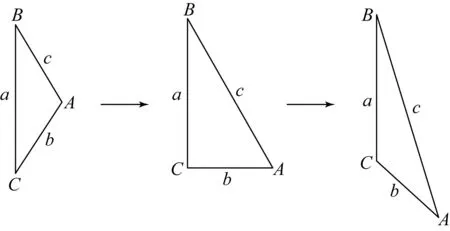
图4
类似还有从柱体与锥体的体积计算公式推广,得到台体体积的计算公式,用归纳法推广数学命题与公式时要学会归纳方法,鼓励学生敢想,敢猜,发展学生的直觉思维,并且在推广的过程中可以通过特例不断修正自己的猜想。
(二)类比推理法
模式2、模式4和模式5主要体现的思想方法就是类比法,德国天文学家开普勒非常重视类比的科学作用,他说:“我珍视类比胜于任何别的东西,它是我最可信赖的老师,它能揭示自然的所有奥秘。”类比推理就是根据对象或事物A、B间存在着的相同或相似属性,联想到另类事物B也可能是具有某种属性的思维方法。我们一般把A称类比源,B称为靶对象。如果我们没有认识到类比源和靶对象的某种(形式上、结构上与内容上)相似性,类比推理无法继续进行。

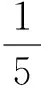
(三)逻辑演绎法
归纳推理法与类比推理法都是合情推理的,得出的命题都是猜想,需要用数学的方法给予证明,在推广数学命题时,为了命题推广的正确性,必要时还需要寻求逻辑推理支持与帮助,这方面最典型的例子就是对数的除法的重新认识。

用逻辑推理法推广的命题正确性得到了保证,但要注意学生的接受能力,就像上面例子中的基本事实何时呈现才合理,才能被学生广泛接受;另外,还要考虑到推广的命题与其他命题之间是否产生认识上的矛盾,如何处理这些矛盾,是教师必须正视的问题。
(四)要素交合法
“主要是对要推广的命题进行结构分解,按序找出若干要素,将每个要素的性质、状态、层次、特征等用直线表示成信息标轴;然后将各标轴上信息交叉进行交合,得到不同预选方案。”[4]从而推广出一些命题,当然有些命题很显然不正确,删去,保留可能正确的命题进行探讨与研究。
如大家熟悉的等式性质:等式两边同时加上或减去同一个数,所得结果仍然是等式。我们把这个命题进行分解,找出三个要素——等式、加上或减去、数,并且寻找与之相似的另外三个要素,即:等式—不等式;加上或减去—乘以或除以—乘方与开方;正数—负数—字母。
我们可以通过要素交合法,得到一系列推广:
(1)等式两边同时乘以或除以同一个数(正数),所得结果仍是等式。
(2)不等式两边同时乘以或除以同一个数(正数),所得结果仍是不等式(不等号方向不变)。
(3)不等式两边同时乘以或除以同一个数(负数),所得结果仍是不等式(不等号方向不变)。
(4)等式两边同时加上或减去同一个字母,所得结果仍是等式。
(5)不等式两边同时加上或减去同一个字母,所得结果仍是不等式(不等号方向不变)。
(6)等式两边同时乘以或除以同一个字母,所得结果仍是等式。
(7)不等式两边同时乘以或除以同一个字母,所得结果仍是不等式(不等号方向不变)。
(8)等式两边同时乘方与开方,所得结果仍是等式。
(9)不等式两边同时乘方与开方,所得结果仍是不等式(不等号方向不变)。
对于分数的基本性质“分数的分子和分母同时乘以或者除以相同的数(除外),分数的大小不变”。有兴趣的老师和同学不妨用“要素交合法”把该性质进行推广。
通过要素交合法推广得到的命题,要做好认真的筛选,哪些是显然不成立的命题,哪些是值得进一步验证与证明的命题,再在其中挑选出探讨价值比较高的问题继续研究。但在用该方法把命题推广时,要注意的是发散式思维很容易出错。
最后我们必须强调一点:推广的万能方法是没有的,唯一的办法是自己要敢想、敢做,不怕错;计算、推理,去实践。
三、数学推广的教育价值
数学推广不仅是一种重要的数学研究手段,也是一种重要的数学学习活动,具有丰富的教育价值,我们要注重挖掘与弘扬它的教育价值,让数学推广成为发展学生数学学科核心素养的重要途径。
(一)培养问题意识,拓宽学生发现问题、提出问题的渠道
《义务教育数学课程标准(2022年版)》(下文简称《课标2022》)把“四能”(发现问题、提出问题、分析问题和解决问题的能力)作为数学课程的总目标之一,“四能”中发现问题与提出问题能力尤为重要,这是因为问题是思维的起点和动力,发现问题并提出问题往往比解决问题更具创造的成分。广大数学教育工作者在教学实践过程中总结出一些富有成效的方法,培养了学生发现问题、提出问题的能力,如在数学情境中、在反思性数学教学中、在类比与比较中培养学生提出问题的能力。数学推广培养了学生从“小范围”到“大范围”、从“低层次”到“高层次”的问题意识,数学推广模式为学生发现问题、提出问题拓宽了的渠道。中学数学特别是高中数学,非常强调数学问题与解法的推广,小学阶段的数学老师要理解“数学推广”是拓宽发现问题、提出问题的重要渠道,知道如何通过具体内容的教学培养学生的数学推广意识与能力。学生到了中学以后自然就会延续这种意识,能够发现并提出更多、更有价值的数学问题。数学推广过程中强调问题意识以及发现问题、提出问题的培养,希望它们不仅仅在学生学习数学时发挥作用,也能迁移到其他学科的学习和工作中。
(二)发展直觉思维,落实学生创新意识、创新能力的培养

(三)体验研究历程,养成学生独立思考、理性思考的习惯
数学推广的过程本身就是数学研究的过程。首先,要思考能不能推广,不能想当然,需要理性思考。如有人利用分数的基本性质推导出分数除以分数的算法,即除以分数等于乘以它的倒数,具体过程如下:

(四)完善数学认知,促进学生基本原则、基本思想的理解

总之,数学推广不仅是数学自身发展的需要,也是落实数学学科核心素养的有效路径,教师要就数学推广操作层面的具体策略展开深入研究,熟悉数学推广的模式,了解数学推广背后的思想方法,在课堂教学中有意识引导学生开展数学推广活动,丰富了数学教与学方式,加深对数学本质理解的同时,注重弘扬数学推广的教育价值,为国家建设培养出一大批高质量的创新型人才。▲
