时变拓扑卫星集群分布式自主相对导航方法
2023-02-28龚翼飞李克行
李 爽,龚翼飞,李克行,刘 旭,曹 凯,王 沙
(1.南京航空航天大学航天学院,南京 211106;2.北京控制工程研究所,北京 100094)
0 引 言
随着航天技术的快速发展,对卫星应用的需求也日益增加,依赖单颗卫星完成各种复杂飞行任务的传统方案存在着成本高、难度大、灵活性低等缺点[1-3]。分布式卫星系统(Distributed satellite system,DSS)是由多颗卫星构成并协同完成特定功能的系统,在研制成本、灵活性、安全性等方面具有优于单颗卫星系统的独特优势,因而得到了越来越多的关注和研究[4]。相对导航技术是确定卫星集群间相对位置速度的关键技术,有助于提升集群系统的整体定位精度和保障复杂任务的顺利高效执行,具有重要的研究意义。
分布式相对导航通过相对导航敏感器获得相对测量信息,然后采用滤波方法实现相对信息融合与估计。其中,相对导航测量敏感器主要有相对GPS、微波雷达、激光雷达、相机等[5-8]。基于GPS载波相位差分的相对导航系统在工程中应用广泛[9],但易受到外部干扰,且信号中断后重新捕获会对高动态系统的实时性造成严重影响[10]。基于无线电和相机等设备的测距测角导航方式,具有设备相对简单、可靠性高等优势,可以降低系统的复杂度,已经成为了相对导航领域的研究热点[11-12]。尽管仅测角相对导航技术已经得到了较为广泛的研究,但光学测角敏感器容易受到光照时间窗口约束的限制而无法正常工作[11,13-14]。在光学测量失效时,可靠性强且对空间环境不敏感的测距敏感器仍可继续工作[15]。譬如,基于到达时间的无线电链路测量或激光雷达测量[16],可为导航系统提供相对距离信息,但视线角信息的缺失会带来目标轨道模糊性的问题。因此,仅测距相对导航不可观/弱可观的问题开始受到关注。解决仅测距相对导航模糊轨道问题常用的方法有轨道机动法[17-18]、传感器偏置法[15,19-20]、多航天器测量法[21-22]、非线性模型法[23-27]等。文献[28-29]通过在编队飞行相对导航中引入一致性约束,解决了近圆轨道仅测距相对导航的不可观测问题,并使用李导数的可观测性判据证明了一致性估计对系统可观测性的改进。但上述算法仅考虑了观测卫星与目标卫星之间的相对状态估计,缺少对大规模集群卫星之间通讯网络的设计。
文献[30]以四星编队为例,设计了一种日地L2点编队卫星的分布式相对导航系统,每颗卫星通过与主星及另一颗从星相互测量得到测距信息,从而实现局部的状态估计,但这种方法也依赖于唯一的主星,并没有实现完全的分布式相对导航。文献[31]对具有固定通信拓扑的分布式系统进行了研究,将AFF(Autonomous formation flying)传感器输出的伪距和相位作为观测值,设计了分布式的相对状态估计系统。此外,当节点卫星只能获得与其相邻卫星之间距离时,分布式算法易陷入局部极小值的问题。为此,文献[32]提出了一种完全分布式定位算法,将节点卫星与相邻卫星的随机子集进行交互,通过合理地构造和更新估计值以及相应的协方差矩阵,融合内部节点信息。文献[33]使用星间相对距离测量,提出了可用于集中式、分散式和分布式网络配置的集群相对定位算法。当前分布式相对导航方法主要针对具有固定拓扑结构的卫星集群,但在网络节点信息拓扑周期性变化情况下,当发生节点运行所导致的可预测连接变化,或节点损毁、链路失效等非可预测突发情况时,为了保持网络的鲁棒性和快速收敛,需要实时地对网络信息拓扑结构进行重新计算[34-35],因此亟待发展适用于时变拓扑星群的分布式相对导航方法。
本文针对地球同步卫星集群的相对导航需求,提出了基于图论的时变拓扑下的分布式相对导航方法。首先建立了卫星集群相对导航的测角测距测量方程和构造了无迹卡尔曼滤波算法,然后针对仅测距相对导航系统的不可观/弱可观问题,提出基于矢量环一致性约束的分布式一致性无迹卡尔曼滤波算法,以提高系统的可观度;其次,针对卫星集群拓扑的时变特性,利用图论相关概念,在Dijkstra算法的基础上考虑拓扑结构对导航滤波精度的影响,对卫星集群拓扑结构进行重构;最后,通过仿真验证了基于一致性无迹卡尔曼滤波的时变拓扑卫星集群分布式相对导航的可行性和鲁棒性。
1 分布式相对导航系统模型
1.1 系统状态方程
首先对卫星集群的相对运动进行建模,作如下假设:
(1)忽略主动控制和摄动影响;
(2)卫星轨道为圆轨道或近圆轨道;
(3)星间距离相对轨道半径可忽略不计。
本文考虑的应用场景为地球静止轨道(Geostationary orbit,GEO)上的近距离卫星集群系统,因此以上假设均可认为成立。基于以上假设,采用Hill-Clohessy-Wiltshire(HCW)动力学方程对相对导航系统状态方程进行建模,这是描述航天器相对运动最广泛使用的模型,仅包括来自二体相对运动模型的一阶泰勒展开线性项。
系统状态量表示为:
(1)
式中:ri为卫星i的位置矢量;vi为卫星i的速度矢量;rij为卫星j相对卫星i的位置矢量;vij为卫星j相对卫星i的速度矢量。上标表示矢量所投影的坐标系,Oi为卫星i的轨道系;下标表示卫星编号。
在卫星轨道坐标系下,利用HCW方程可以得到如下的相对导航系统状态方程:
(2)
式中:G(k)为已知噪声驱动矩阵;W(k)为过程噪声,假设是均值为零的高斯白噪声,协方差矩阵为Q。
(3)
(4)
(5)
(6)
式中:n为主卫星轨道角速度;t为时间间隔。
1.2 系统测量方程
考虑到GEO及更高轨道上GPS导航困难,本文选择光学相机和星载数据链为测量敏感器,以卫星之间的相对距离和相对角度信息作为相对导航系统的测量信息,在卫星轨道坐标系中得到如下的测量方程:
(7)
式中:h1为俯仰角,h2为偏航角,h3为视向距离,表达式如式(8)至式(10)所示。V(k)为观测噪声,假设为加性均值为零的高斯白噪声,协方差矩阵为R,假设观测噪声与过程噪声互不相关。
(8)
(9)
(10)
太空环境复杂多变,相机成像距离受到相机分辨率限制,光学相机还会受到光照时间窗口的约束,导致相对导航中相机失效无法完成光学测量的情况时有发生,此时,仅测距敏感器可用,可观测的相对测角测距导航系统退化为不可观测的相对测距系统,式(7)所示的测量方程退化为:
(11)
1.3 信息融合与状态估计
多传感器信息融合方法根据结构的不同可以分为集中式融合和分布式融合方法。集中式融合方法即系统的测量信息输入到一个滤波器中,对所有待估计状态量进行同步估计,在卫星数量增加时,系统的状态维度加大,对星上的实时计算将会带来挑战。分布式融合方法具有设计简单方便、计算负担小、可靠性高等优点,根据是否具有主航天器可分为分层分布式融合和完全分布式融合。分层分布式融合将滤波器分为多层,底层滤波器处理系统的测量信息,其余层滤波器处理来自上一层的信息;完全分布式融合不存在主滤波器,各个滤波器之间互相交换数据与信息。
本文采用分布式导航系统,每颗卫星只需要处理自己与相邻卫星之间的测量数据,估计出对应的相对状态信息,并将所得的状态信息传递给相邻卫星(如图1所示),最终实现所有系统状态的全局估计。针对1.2节中所述的测量不完备情况,以可以形成最小网格的三颗卫星系统为例,根据星间测量受损的严重程度,设计了以下三种状态估计算法:

图1 分布式导航结构示意图Fig.1 Illustration of the distributed navigation structure
1)全连通相对导航系统
当三颗卫星间的测角测距条件都满足时,测量条件最优,状态方程如式(2),测量方程如式(7),系统的测量拓扑结构图如图2所示,图中矢量箭头表示卫星间的相对角度和距离测量。
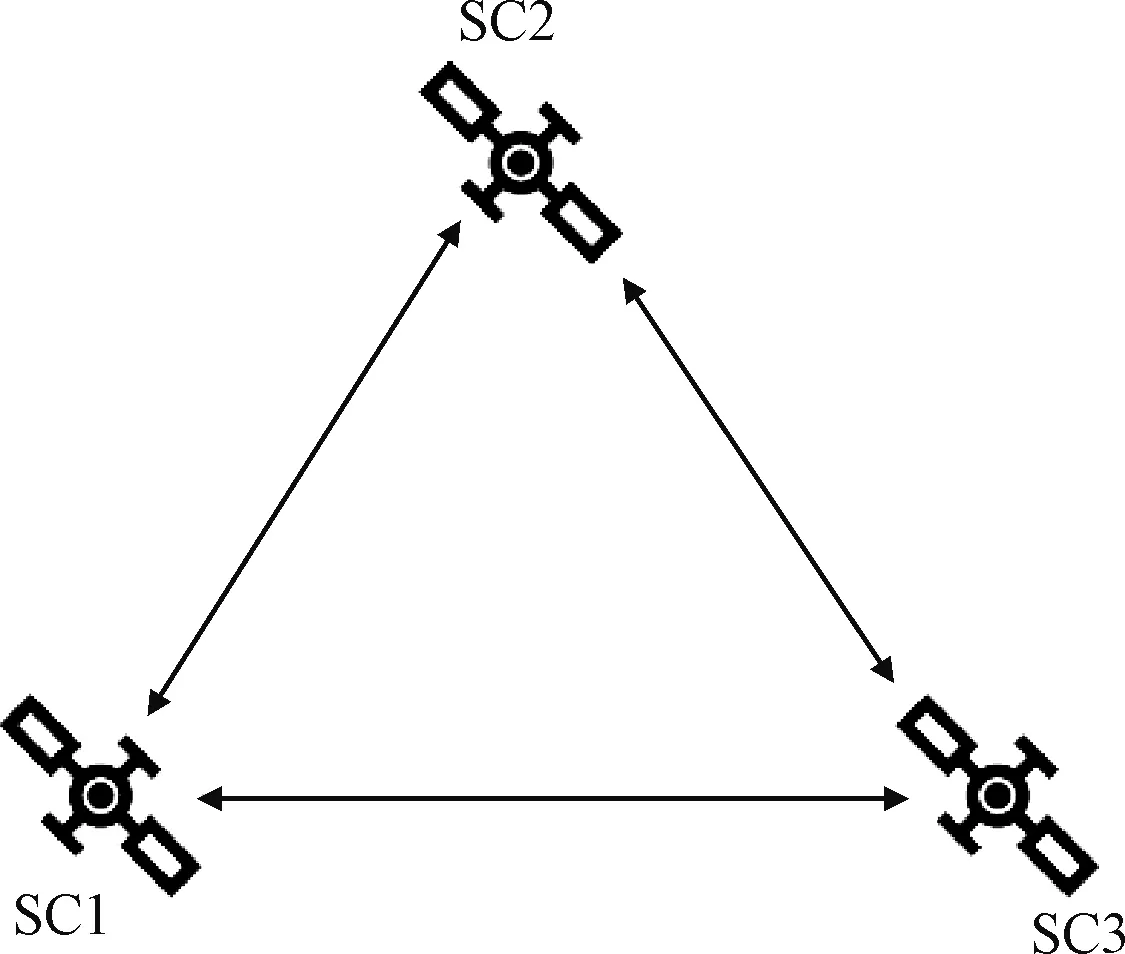
图2 全连通系统测量拓扑图Fig.2 Measurement topology of the fully connected system
针对系统的强非线性,选用无迹卡尔曼滤波(Unscented Kalman filter,UKF)进行数据融合和状态估计,具体计算公式如下所示:
(1)使用UT(Unscented transform)变换,计算一组sigma采样点集及其对应的权值。
(12)
式中:n为状态量维数,在此系统中n= 6。
(2)计算sigma点集的一步预测。
X(l)(k+1|k)=f(k,X(l)(k|k))
(13)
(3)计算系统状态量的一步预测及协方差矩阵。
(14)
(15)
(4)根据一步预测值再次使用UT变换产生新的sigma点集。
(16)
(5)将sigma点集代入观测方程(7),得到预测观测值。
Z(l)(k+1|k)=h(X(l)(k+1|k))
(17)
(6)由预测观测值加权求和得到系统预测的均值和协方差。
(18)
(19)
(20)
(7)计算卡尔曼增益。
(21)
(8)计算系统的状态更新和协方差更新。

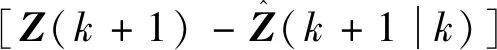
(22)
P(k+1|k+1)=P(k+1|k)-K(k+1)·
PzzKT(k+1)
(23)
2)半连通相对导航系统
当三颗卫星中存在两颗卫星无法进行相对角度测量时,即有一条测量链路中断时,系统的测量拓扑图如图3所示。图中实线箭头矢量表示卫星间进行相对测角测距,虚线箭头矢量表示卫星间相对角度测量失效。
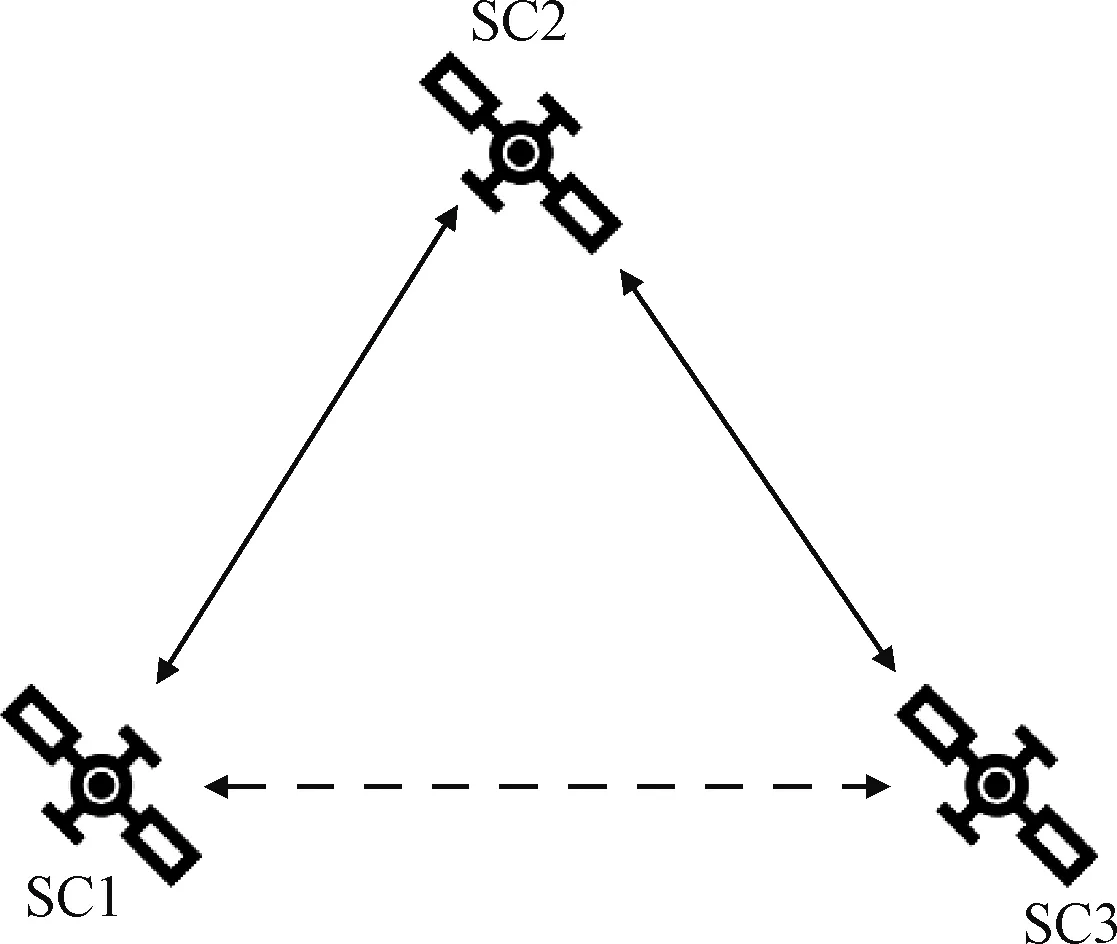
图3 半连通系统测量拓扑图Fig.3 Measurement topology of the semi connected system
此时SC1与SC2、SC2与SC3之间的状态方程与测量方程同全连通系统,SC1与SC3之间仅能进行相对距离测量,在仅有相对距离信息的情况下实现相对导航,属于测量信息不完备情况下的相对导航技术[12]。因此引入几何约束,根据SC1与SC2、SC2与SC3间滤波得到的后验相对状态量转换得到SC1与SC3之间的相对状态估计值,如式(24)所示。
(24)
式中:上标I表示惯性系。
转换到轨道坐标系下:
(25)
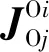
(26)
式中:Rji表示从j号航天器到i号航天器的旋转矩阵;ωi表示i号航天器相对于惯性系的角速度在Oi中的投影。
3)不连通相对导航系统
当三颗卫星间存在两条测量链路失效时,系统的测量拓扑结构图如图4所示。

图4 不连通系统测量拓扑图Fig.4 Measurement topology of the disconnected system
此时SC2与SC3、SC1与SC3间都仅支持相对距离测量,视线角信息的缺失会带来目标轨道模糊问题,直接进行滤波会导致此局部相对导航系统不收敛,无法精确地完成相对状态估计,从而导致星群相对导航系统的发散。

从可观性的角度来看,一般来说,只要在系统上添加附加约束,系统的可观测度就会提高[29]。接下来对此系统的可观性进行理论分析。
文献[25]研究表明,具有相同距离信息的模糊轨道一共有七条,如表1所示。

表1 仅测距模糊轨道类型Table 1 Types of ambiguous orbits based on range-only measurements
表中的(t)轨道表示真实轨道;(a)~(c)为镜像模糊轨道,与真实轨道形状相似;(d)~(g)为变形模糊轨道,其平面内和平面外运动的幅度与真实轨道不同,上标~表示变形量。
在不连通系统的测量条件与矢量环一致性约束下,若存在模糊轨道,则模糊轨道的状态X′12(t),X′23(t),X′13(t)需要满足如下的约束方程:
(27)
而表1的七种模糊轨道中不存在同时满足式(27)的轨道,这表明矢量环一致性约束下的仅测距相对导航系统不存在长期稳定的模糊轨道,系统的可观度得以提高,可观性能够得到满足。


图5 航天器测量与通信拓扑图Fig.5 Spacecraft measurement and communication topology
时间更新方程、协方差测量更新方程和UKF算法相同,下面仅给出CUKF算法的状态测量更新方程:
Xk+1=Xk+1|k+K[Z-h(Xk+1|k,0)]-
(28)
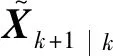
2 时变拓扑结构重构
卫星集群的通讯网络是一个时变拓扑结构,网络中各个卫星之间的连通情况由卫星间所满足的测量条件决定。上一节以三颗卫星系统为例,给出了不同测量条件下的固定拓扑结构,当卫星集群数量增大时,拓扑结构需要根据各个卫星节点之间的测量情况进行动态调整,即对拓扑结构进行实时设计与重构。为此,本节基于图论的思想,设计了一种以滤波精度为导向的改进Dijkstra算法来动态确定卫星集群的拓扑结构,为后续采用一致性无迹卡尔曼滤波算法完成分布式相对导航提供基础。
2.1 图论基础
无向图G由点集VG=[1,…,N]和边集εG⊂VG×VG定义,其中N为节点数目。若(i,j)∈εG,则表明节点i和节点j是连通的,表示为i~j。单个节点的度由与之相连的节点数目决定,定义di为节点i的度,则图G的度矩阵D(G)∈RN×N表示为:
D(G)=diag(d1,…,dN)
(29)
路径i0i1…iL为一个有限节点序列,其中ik-1~ik,k=1 …L。若在任意一对不同的节点之间至少有一条路径,则图G是连通图。
定义图G的邻接矩阵A(G)∈RN×N如下所示:
(30)

2.2 改进的Dijkstra算法
卫星集群既有自组织网络无中心、自治、动态拓扑等特性,又具有卫星在轨运行时轨道已知且周期性变化等特点。对于角度测量时变失效的测距测角相对导航系统而言,能够根据通信链路失效状况进行实时的拓扑重构,对于提高导航系统的鲁棒性与精度具有重要意义。本节基于图论中Dijkstra最短路径规划算法,结合后验状态估计误差精度,设计了一种自适应的时变网络拓扑结构优化算法。
经典Dijkstra算法解决的是有向图上单源点最短路径规划问题。Dijkstra算法把图中所有节点分为两组:集合V表示已经求出最短路径上的节点的集合,初始状态为空集;集合T表示集合V之外所有节点的集合。把集合T中节点按权值非减的次序排序,并按此顺序依次加入到集合V里。V中节点表示的距离是从出发点v0到该集合中每一个节点的最短路径长度,集合T中所有节点表示从出发点v0到T中所有的节点且只经过V中节点作为中间节点的最短路径长度。
在卫星集群相对导航系统拓扑结构图中,同一时刻从节点v0到节点vn可能会有多条长度相同的路径,此时经典Dijkstra算法将优先选择编号总和最小的航天器节点路径,但在编号随机的集群系统中,这个选择是无意义且非最优的。而在导航滤波中,不同航天器间的滤波精度由于测量条件、建模精度等的不同具有显著差异,如果能将滤波精度作为优化目标引入到路径规划的算法中,将对提高导航系统拓扑结构设计的效率与可靠性大有帮助。将状态估计误差协方差矩阵对角元素作为Dijkstra算法中的路径权重,对最短路径规划加以约束,则基于滤波精度的Dijkstra算法可描述为:
设置辅助数组dist,其中每个分量dist[k]表示当前所求得的从源点v0到其余各顶点k的最短路径。
(1)V= {v0};
(2)设置集合T中各顶点的初始距离值为对应航天器的上时刻后验状态估计误差协方差;
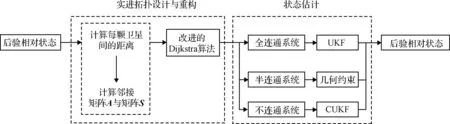
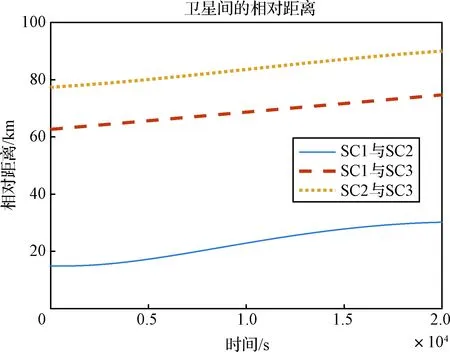
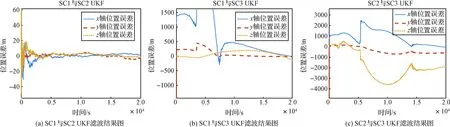
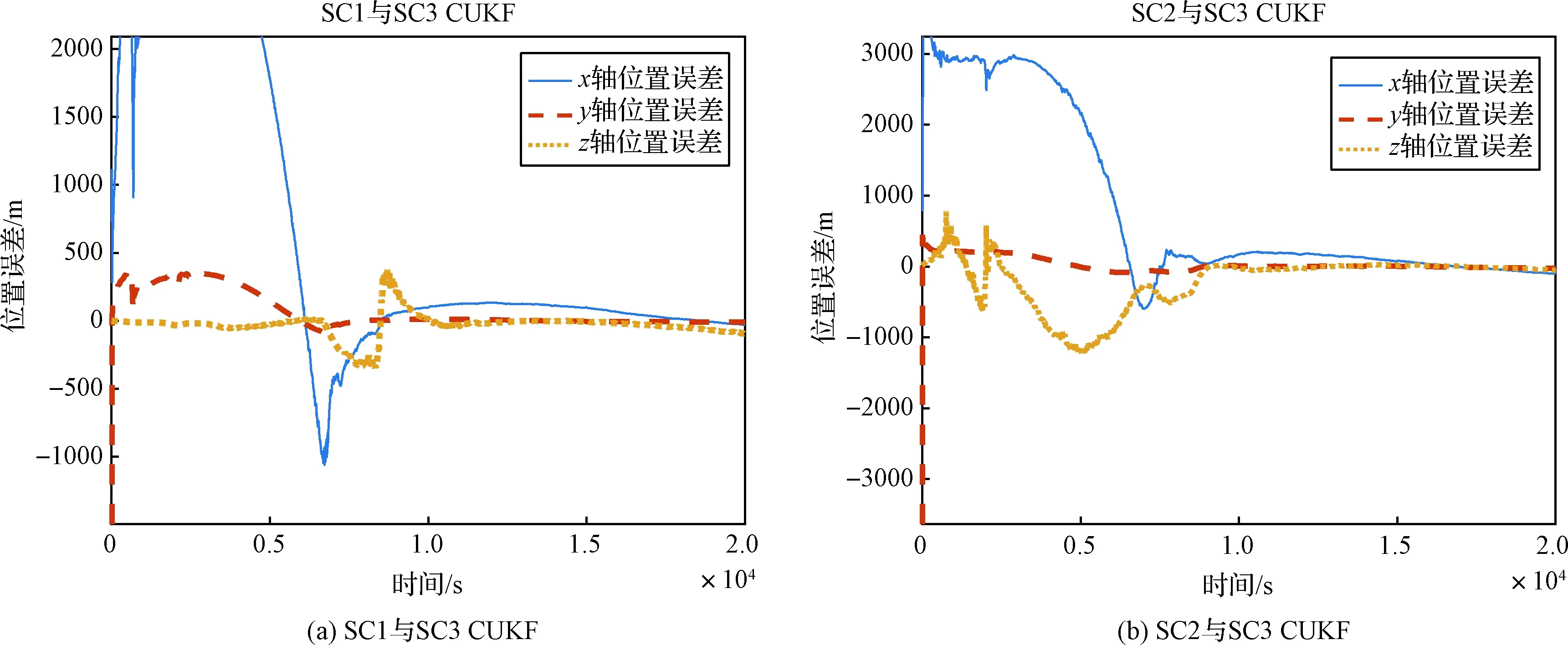
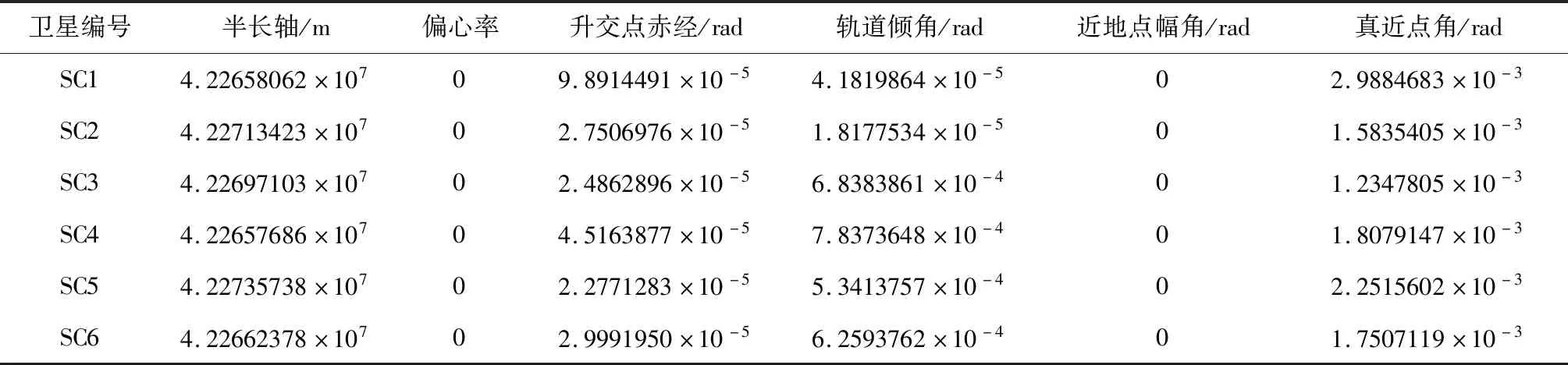
(3)while (集合V中顶点数 {在集合T中选择距离最小的顶点vj; V←V+{vj}; 调整集合T中顶点的距离值;} 在每一步滤波过程中,首先需要对当前时刻的星间拓扑结构进行设计,具体方法为:根据上一时刻的后验估计相对状态,计算出相邻卫星之间的距离,若满足相对测角测距条件,即相对距离小于光学相机成像阈值时,邻接矩阵对应元素置1,否则置0,从而计算出当前时刻卫星集群系统的邻接矩阵A和连通矩阵S;然后利用改进的Dijkstra算法对卫星间的测量与通信路径进行规划,设计出时变网络的拓扑结构。 得到星群的拓扑结构之后,对导航系统的状态进行估计:卫星间根据测量条件的不同可分为全连通系统、半连通系统与不连通系统,全连通系统采用无迹卡尔曼滤波算法,半连通系统根据几何约束得到状态估计,不连通系统采用矢量环一致性约束下的一致性无迹卡尔曼滤波算法,从而得到当前时刻系统状态的后验估计。时变拓扑下的分布式相对导航算法流程框图如图6所示。 图6 时变拓扑分布式相对导航算法流程图Fig.6 Flow chart of time-varying topology of the distributed relative navigation algorithm 本节针对所提出的算法分别进行了仿真验证。3.1节建立了一个固定拓扑下的不连通三星相对导航系统,分别采用UKF与构造的CUKF算法进行状态估计,以验证测量不完备情况下CUKF对系统可观测度的影响。3.2节建立了一个四星的相对导航系统,需要实时地对拓扑结构进行设计,在此分别采用了经典的Dijkstra算法与改进的Dijkstra算法,以验证改进算法可以带来的导航精度上的改进。3.3节建立了一个GEO轨道六星系统,在此系统中应用了2.3节所描述的时变拓扑分布式相对导航算法,以验证提出的算法在更大规模集群系统中的可行性与鲁棒性。 首先选取一个三颗卫星组成的固定拓扑结构系统对提出的CUKF算法进行验证。 三颗卫星的轨道根数设置如表2所示。设置仿真时间为20000 s,步长10 s,三颗卫星间的相对距离如图7所示。 表2 卫星初始轨道六根数Table 2 Initial orbit elements of satellites 图7 卫星间的相对距离Fig.7 Relative range between satellites 假设当星间距离大于40 km时,卫星间光学测量方式失效,无法获得相对角度信息。由图7可知,在仿真过程中,SC3与另外两颗卫星之间的距离始终大于40 km,只能得到仅测距信息;而SC1与SC2之间可以获得测角测距信息,根据1.3节中所述的三种导航系统分类定义,此系统为固定拓扑下的不连通系统。 设置SC1与SC2间的初始状态误差为:[1×103,2×103,1×103,0,0.02,0.2]T,(前三项单位:m,后三项单位:(m·s-1);如无特别说明,下文与此处相同)。初始误差协方差为:diag(510,510,510,1,1,1)。SC3与其他卫星间的初始状态误差为:[800,1.5×104,50,0,0.1,0.4]T,初始误差协方差为:diag(6×106,2×109,3×103,1,1,1)。测角测距测量噪声协方差为:diag(100,0.052,0.052)(第一项单位:m,后两项单位:(°));仅测距测量噪声协方差为:100 m。 使用传统的无迹卡尔曼滤波算法对此系统进行状态估计,得到的结果如图8所示。 图8 固定拓扑下不连通系统UKF滤波结果Fig.8 UKF result of the disconnected system in fixed topology SC1与SC2之间可以得到充足的相对测量信息,因此可以很快地达到收敛,收敛后精度在±2 m左右。而相对地,SC3与其他卫星之间由于测量信息的不足,滤波收敛速度很慢,状态估计的误差也远远大于SC1和SC2之间的状态估计误差。 在同样的参数设置下,引入矢量环一致性约束下的CUKF算法,令一致性反馈项γ=0.03,得到的滤波结果如图9和表3所示。 表3 CUKF与UKF滤波结果对比Table 3 Comparison of the filtering results between CUKF and UKF 根据图8图9可以看出,CUKF相较UKF的收敛速度大大加快;根据表3可以看出,CUKF合位置误差的均方根误差(Root mean square error,RMSE)降低了50%以上,但单次滤波耗时增加不到4%。由此可见,一致性约束的引入对于解决不完备测量下可观测度不足的问题有很大帮助,导航系统在收敛速度和精度上都有了较大的改善,且带来的计算时间上的增加是可以接受的。 图9 固定拓扑下不连通系统CUKF滤波结果图Fig.9 CUKF result of the disconnected system 本节采用一个四颗卫星组成的系统对所提出的改进Dijkstra算法进行验证,卫星的轨道根数设置如表4,仿真时间为1000 s,步长10 s。不同于基础的三星系统,四星系统需要实时地对通信与测量链路进行规划,在此分别采用传统的Dijkstra算法及以滤波精度为优化目标的改进Dijkstra算法来完成拓扑设计。 表4 星群初始轨道六根数Table 4 Initial orbit elements of the satellite cluster 设置除SC2外各卫星间的初始状态误差为[1×103,2×103,100,1,2,0.1]T,状态误差协方差为diag(1.8×106,1.8×106,1.8×106,1.8,1.8,1.8)。SC2与其他卫星的初始状态误差为[1×104,2×104,1×103,10,20,1]T,状态误差协方差为diag(1.8×108,1.8×108,1.8×108,180,180,180)。其余参数同3.1节。 在仿真过程中,SC1与SC4之间距离大于所设阈值,满足1.3节定义的半连通系统,需要进行实时的拓扑设计,分别采用传统Dijkstra算法与改进Dijkstra算法,得到的滤波结果如表5所示。 由表5可以看出,改进Dijkstra算法在单次滤波耗时增加不到10%的前提下,x轴和y轴方向的状态估计均方根误差分别降低了72.6%和92.0%,在滤波精度上的提高效果足以得到验证。需要注意的是,本节为了体现所提出算法能够带来的滤波精度上的改进,刻意放大了卫星间的状态误差,在实际仿真过程中可能并不会有如此大的差异,但同样能展现出所提算法的优越性。 表5 传统与改进Dijkstra算法下SC1与SC4滤波结果对比Table 5 Comparison of SC1 and SC4 filtering results under traditional and improved Dijkstra algorithms 为验证整体算法在时变拓扑结构星群中的应用效果,本文选取一个具有6颗卫星的GEO轨道星群作为仿真对象,初始轨道根数设置如表6所示。 表6 星群初始轨道六根数Table 6 Initial orbit elements of the satellite cluster 设置仿真时间30000 s,仿真步长10 s。SC1与其他卫星间初始状态误差为[50,5.6×10-3,10,0,0,0.2]T,状态误差协方差为diag(6×103,1×108,100,0,0,0)。其余卫星间的初始状态误差为[1×103,2×103,100,1,2,0.1]T,状态误差协方差为diag(1.8×106,1.8×106,1.8×106,1.8,1.8,1.8)。其余参数同3.1节。仿真结果如图10至图12所示。 图10 不同时刻的系统拓扑结构图Fig.10 System topology at different times 图11 两组卫星滤波结果图Fig.11 Filtering results of two groups of satellites 图12 星群时变拓扑分布式相对导航状态估计均方根误差Fig.12 RMSEs of the satellite cluster relative navigation in time-varying topology 在30000 s的仿真时间内,系统一共完成了五次自主拓扑重构工作,分别发生在t=0 s(即导航开始时刻),4960 s,7650 s,20900 s,28580 s时,自主设计的拓扑结构如图10所示,其中不同形状的点分别表示6颗卫星,实线表示卫星之间为全连通状态,可以直接进行测角测距相对导航;虚线表示卫星之间为半连通状态,通过几何约束进行状态估计;未连线表示卫星之间为不连通状态,需要通过一致性约束下的一致性无迹卡尔曼滤波完成仅测距相对导航。由于卫星数量众多,不便完全展示所有卫星之间的相对状态估计误差,以下选取两组卫星作为展示。 根据图11(b)的滤波结果可以看出,SC3与SC4之间的相对导航可以快速达到收敛,收敛后精度在±2 m以内;由图10的拓扑结构图可知,SC1与其他卫星前期保持半连通状态,后期由于相对距离增加,拓扑结构转变为不连通状态,相应地,状态估计误差相较半连通状态时也会变大,图11(a)的滤波结果印证了这一结论:前期状态误差保持在米级,后期增大到数十米量级,但在所提出的CUKF算法下仍能够将状态误差控制在可控的收敛范围内。 图12为每颗卫星间的状态估计均方根误差(RMSE),其中纵坐标表示状态估计均方根误差的大小,RMSE的值越大,则状态估计误差越大、导航精度越低。可以看出,SC1由于测量条件较差,状态估计的误差相较其他卫星会更大,但根据图11(a)显示,在不完备测量下状态估计误差较大时,系统也可以保证滤波收敛。 仿真结果可以表明,本文所提出的改进Dijkstra算法可以实时地对拓扑结构进行设计与重构,且滤波效果良好,收敛速度和精度都较为理想。 本文针对地球同步轨道卫星集群的相对导航问题,研究了时变拓扑卫星集群的分布式相对导航方法。根据卫星之间测量条件的差异,本文将分布式的相对导航系统分为全连通、半连通、不连通三种情况,并针对不连通系统不可观/弱可观的问题引入矢量环的一致性约束,构造了CUKF算法来解决轨道模糊问题。相较无迹卡尔曼滤波,所提出的CUKF在有限的时间消耗增加下,大大提高了仅测距相对导航系统的收敛速度与状态估计精度。本文还提出了以状态估计精度作为优化指标的改进Dijkstra算法,实现了对系统时变拓扑结构的动态优化,进而结合CUKF实现分布式相对导航。该方法相比基于传统Dijkstra算法的分布式相对导航方法,在鲁棒性和导航精度方面均更优。2.3 时变拓扑星群分布式相对导航方法
3 仿真校验
3.1 CUKF算法对比与校验


3.2 改进Dijkstra算法对比与校验


3.3 时变拓扑星群分布式相对导航系统校验



4 结 论
