星历模型下地月自由返回全飞行过程轨道设计

彭祺擘，和星吉，陈天冀，武新峰，徐 明

(1.中国航天员科研训练中心，北京 100094；2.北京航空航天大学宇航学院，北京 102206；3.北京航空航天大学未来空天技术学院/高等理工学院，北京 100191)

0 引 言

月球是人类进入深空的起点，自1961年启动阿波罗计划[1]至今的六十多年来，人类从未停下探索月球、开发地月空间的脚步。特别是近年来，各航天强国均提出了自己的载人探月计划，人类重返月球的脚步势不可挡。转移轨道设计作为地月空间探测与开发的关键技术之一，是所有地月空间探测任务的基础[2]。一般的地月转移轨道设计只需要满足飞行时间、月面着陆区、测控等基本约束条件即可，轨道设计的空间往往较大[3]。但沿一般转移轨道飞行，飞行器在地月转移过程中发生故障后，在不进行轨道机动的前提下，将无法返回地球，因此其安全性相对较低。

与无人月球探测不同，航天员的安全是载人登月任务的首要考虑因素。由于自由返回方式具有较高的安全特性，且实施过程较为简单，因此载人登月任务通常采用具备自由返回能力的地月转移方案。20世纪60年代美国航天局便已经开始对自由返回轨道展开研究并将其用于阿波罗计划的轨道设计[4]。在自由返回轨道的研究初期，普遍采用的是在二体模型下求解转移轨道初值再进行修正的思想。例如，Carlson[5]通过简单公式和图解法分析了绕月自由返回轨道在月球影响球上的入口点范围，以及入口点范围同相关轨道参数的关系。Battin[6]、陈海萍[7]、黄文德等[8]、Liu等[9]都研究了基于双二体模型的自由返回轨道解析设计方法，并利用此方法进行了大量轨道特性分析。陆林等[12]给出了基于自由返回轨道的载人月球探测转移方案，Li等[10]对多段拼接自由返回轨道设计方法展开了研究，Miele等[11]利用镜像特性对月球与火星任务的自由返回轨道进行了优化设计。该类方法可获得解析的初值，特别是对转移轨道的近地段和近月段有较好的近似效果。但是，由于在地月转移中途地月引力对航天器均具有可观的影响，二体近似结果产生的误差很大。

随着计算机数值计算能力的提高和多体引力场转移轨道研究的深入，研究人员开始在多体模型下对具备自由返回能力的地月转移轨道进行设计。Jesick等[13]给出了圆型限制性三体模型下对称自由返回轨道的设计方法。彭坤等[14]在三体模型下研究了地月空间对称自由返回轨道的设计方法并对4种类型对称自由返回轨道的轨道特性进行了分析。孟占峰等[15]基于改进的三体Lambert算法提出了一种适用于在轨自主生成和实施的绕月自由返回轨道应急制导策略。王艾雪等[16]提出了采用地心顺行月心逆行自由返回轨道进入DRO轨道的方法。上述研究解决了三体模型下的自由返回轨道设计方法，但并未涉及到达月球后的近月轨道进入问题。

基于自由返回轨道的终端变轨方案安全性较高，适用于早期的载人登月任务[17]。考虑到我国尚未实施过载人登月任务，本文在地月三体模型自由返回轨道求解的基础上,对星历模型下的自由返回+近月三脉冲的地月转移全飞行过程轨道设计方法展开了研究。

1 三体模型下的标称自由返回轨道设计

圆型限制性三体问题(CR3BP)研究质量可以忽略的航天器在两个大天体引力作用下的运动，该模型假设两个大天体分别绕其公共质心做圆周运动。在初步设计地月系统内的转移轨道时，可将地-月-航天器所组成的三体问题简化为圆型限制性三体问题。通常，在质心会合坐标系下描述CR3BP中航天器的运动。对于地月系统，会合坐标系的原点与地月系统的质心重合，x轴由地心指向月心，z轴沿月球绕地球转动的动量矩方向，y轴在白道面内由右手定则确定。为了数值运算的方便常常将单位进行归一化，时间、距离、质量的归一化单位分别为TEM/2π,LEM和ME+MM，其中，TEM为月球绕地球转动的周期，LEM为地月距离，ME为地球质量，MM为月球质量，在此规定下，万有引力系数等于1。定义质量系数μ=MM/(ME+MM)，于是会合坐标系下地月的横坐标分别为-μ和1-μ。根据文献[18]，本文取地月系统的μ=0.012150568。会合坐标系下描述航天器的动力学方程为

(1)

式中：

状态转移矩阵(STM)是动力学方程的流函数对初始状态的导数，在CR3BP模型下，状态转移矩阵反映了参考轨道对微小扰动的线性特征，在周期轨道的微分修正和不变流形的计算等方面都有很广泛的应用。对于CR3BP动力学方程，从t0时刻到t时刻的状态转移矩阵Φ(t,t0)满足：

(2)

式中：I6×6为6阶单位阵;A(t)与等效势函数U有关：

(3)

(4)

(5)

(6)

状态转移矩阵Φ(t,t0)的各个分量具有如下物理意义：

(7)

式中：x0和x分别为航天器在t0时刻和t时刻的状态量。

本文采用微分修正的方法在CR3BP模型下对自由返回轨道的初值进行搜索。有关微分修正方法在CR3BP模型下的详细推导和介绍可查阅参考文献[19]，下面仅对微分修正方法在自由返回轨道上的具体应用过程进行介绍。如图1所示，在CR3BP模型下自由返回轨道从高度为hA的近地停泊轨道出发，到达近月距离为hB的环月弧段绕月后返回地球，返回段终点的高度为hC。设航天器在A,B,C点处的状态量为分别SA=[rA,vA],SB=[rB,vB],SC=[rC,vC]。约束为A,B和C点处的速度切向约束rA/B/C·vA/B/C=0，以及高度约束hA,hB和hC，写为矩阵F的形式：

图1 CR3BP下自由返回轨道示意图Fig.1 Schematic diagram of a free return trajectory under CR3BP model

(8)

式中：RE和RM分别为地球和月球的半径。

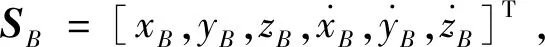
(9)

在采用微分修正算法对自由返回轨道进行求解时，选定的设计变量为：

(10)

式中：tAB和tBC分别为地月转移段和月地转移段的飞行时间。微分修正迭代时，以B点处的状态为初值，沿时间逆向积分tAB得到A点状态，沿时间正向积分tBC得到B点状态。载人登月任务通常要求tAB+tBC<6天，微分修正时可将初次迭代的转移时间初值估计为tAB=tBC=2.5天。

每次迭代更新时的修正量为

δX=-DF-1F

(11)

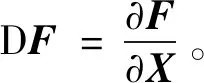
令

(12)

那么

(13)

根据式(7)，式(13)可写作：

(14)

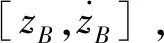
图2 三体模型下自由返回轨道分布情况Fig.2 Free return trajectories distribution under CR3BP model

获得CR3BP模型下的自由返回轨道后，将其作为高精度星历模型下的初值进行寻优和修正，可得到高精度星历下满足工程约束的自由返回轨道。

2 环月三脉冲机动设计

航天器沿自由返回轨道实现地月转移后，需在月球临近区域进行一系列的轨道机动进入目标环月轨道。通常采用如图3所示的三脉冲机动方式：当航天器沿自由返回轨道到达近月点时，实施一次制动脉冲进入环月大椭圆轨道，实现月球引力捕获；之后，在大椭圆轨道远月点附近进行一次变平面机动，目的是改变轨道平面以满足目标环月轨道面的约束；第三次机动则是近月点圆化，使航天器进入目标近月圆轨道。采用该自由返回+环月三脉冲变轨的地月转移方案，在三脉冲开始前的奔月过程中出现故障均可沿自由返回轨道实现无动力返回，具有安全性高的优点。

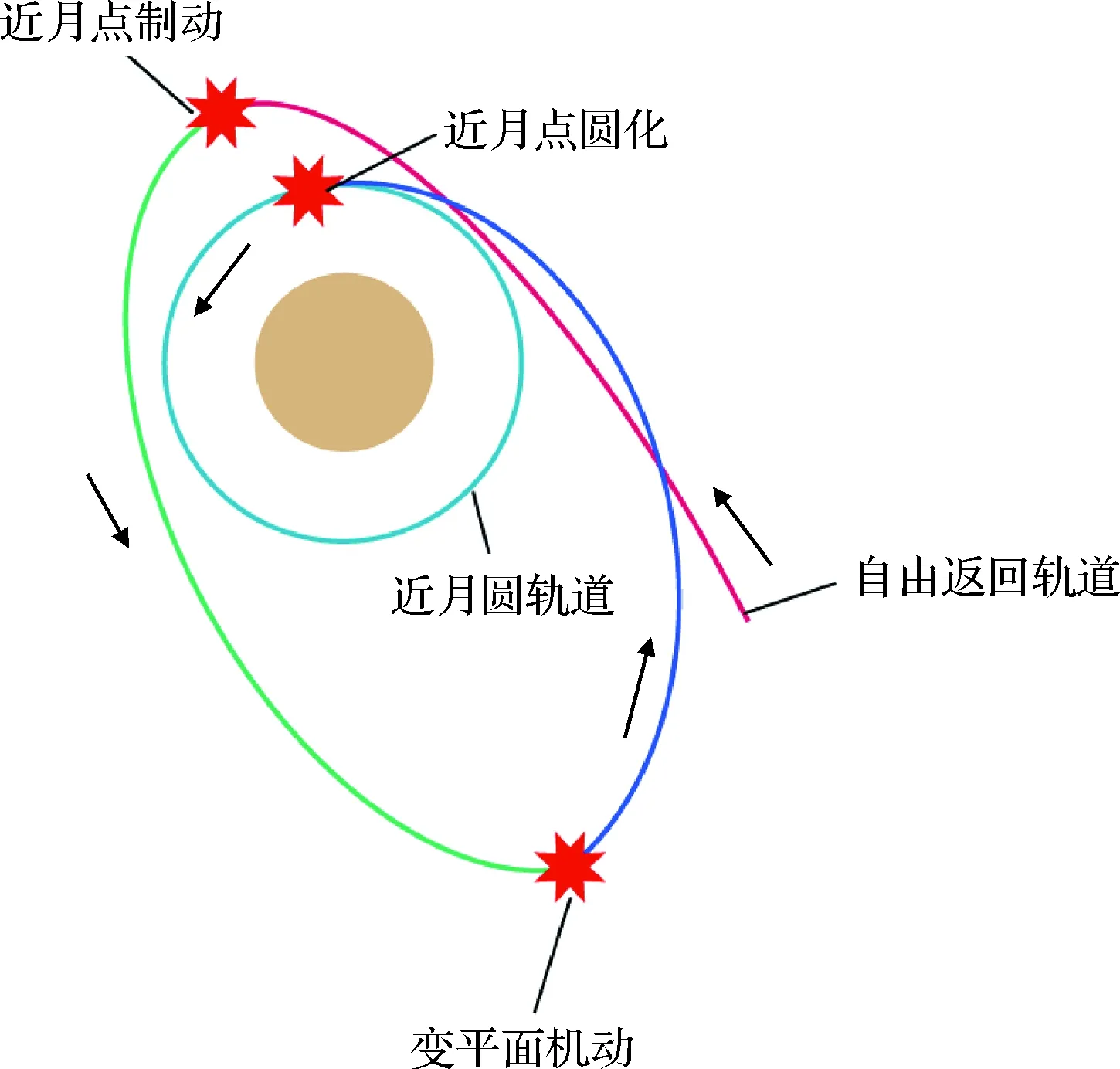
图3 环月三脉冲机动示意图Fig.3 Schematic diagram of the lunar three-pulse maneuver

假设三次机动的脉冲分别为ΔvM1,ΔvM2和ΔvM3。由于三脉冲变轨是在月球附近实施的，地球引力的影响不大，因此在计算初值时可仅考虑月球引力影响，在二体模型下进行求解。第一和第三次机动均是在近月点施加的制动脉冲，用于改变半长轴，其方向与近月点处机动前的速度方向相反，大小满足：

(15)

图4 变平面机动示意图Fig.4 Schematic diagram of orbital plane changing maneuver

图5 变平面机动脉冲Fig.5 Orbital plane changing maneuver

机动前的轨道径向速度大小为

(16)

(17)

(18)

进而可得到变倾角机动需要的脉冲

(19)

3 星历模型下的地月转移轨道优化修正

三体模型考虑了地球、月球引力同时作用下的航天器运动，适用于对于地月空间探测轨道的初步设计和航天器轨道演变规律的探寻。然而，三体模型或其他近似模型忽略了系统的真实偏心率以及空间中其他天体的引力等摄动因素，直接将这些模型下的结果用于工程设计是不够可靠的。因此，在三体等近似模型的基础上，需要考虑各天体实际的位置情况以反映地月空间内飞行时真实的轨道动力学环境，天体的位置可由高精度星历提供。J2000地球平赤道坐标系下建立的航天器星历模型如式(20)所示。

(20)

式中：μE为地球引力常数；Fi是各天体的引力摄动，该模型详细推导以及与三体动力学模型的相互转换可从文献[20]得到。DE430星历模型[17]考虑了太阳以及各行星的引力摄动，可准确反映真实天体引力摄动对轨道的影响。

若直接将三体模型和二体模型下得到的轨道初值在星历模型下进行积分，各种摄动的影响会导致得到的转移轨道产生较大偏差。例如，当近地出发点高度hA= 170 km、近月点高度hB= 200 km时，将CR3BP模型下的近月点状态作为起点在星历模型下进行逆向积分：若积分时长设为与在CR3BP模型下得到的地月转移时长一样，那么积分停止点处的轨道高度为35418 km，此时的积分停止点并不是星历模型下的近地点；但如果将星历模型下的逆向积分停止条件设置为在近地点处停止，得到的近地出发高度则为181 km，并且此时的逆向积分时长并非CR3BP模型下得到的地月转移时长。可见，直接将三体模型下的结果用于星历模型确实会产生较大偏差。因此，本节将三体模型下获得的自由返回轨道和二体模型下的近月三脉冲机动作为初值，在DE430星历模型下进行寻优和修正，得到星历模型下满足约束的地月转移轨道。

在星历模型下，由于历元时刻对白道面、地月距离和地月相位关系的影响较大，因此需要对航天器在近地停泊轨道上的奔月出发位置进行优化修正。为了提高星历模型下自由返回轨道优化修正的收敛性，如图6所示，本文采用先以近月点为起始点的第一层优化，后以近地轨道出发点为起始点的第二层优化相结合的两步优化修正策略。

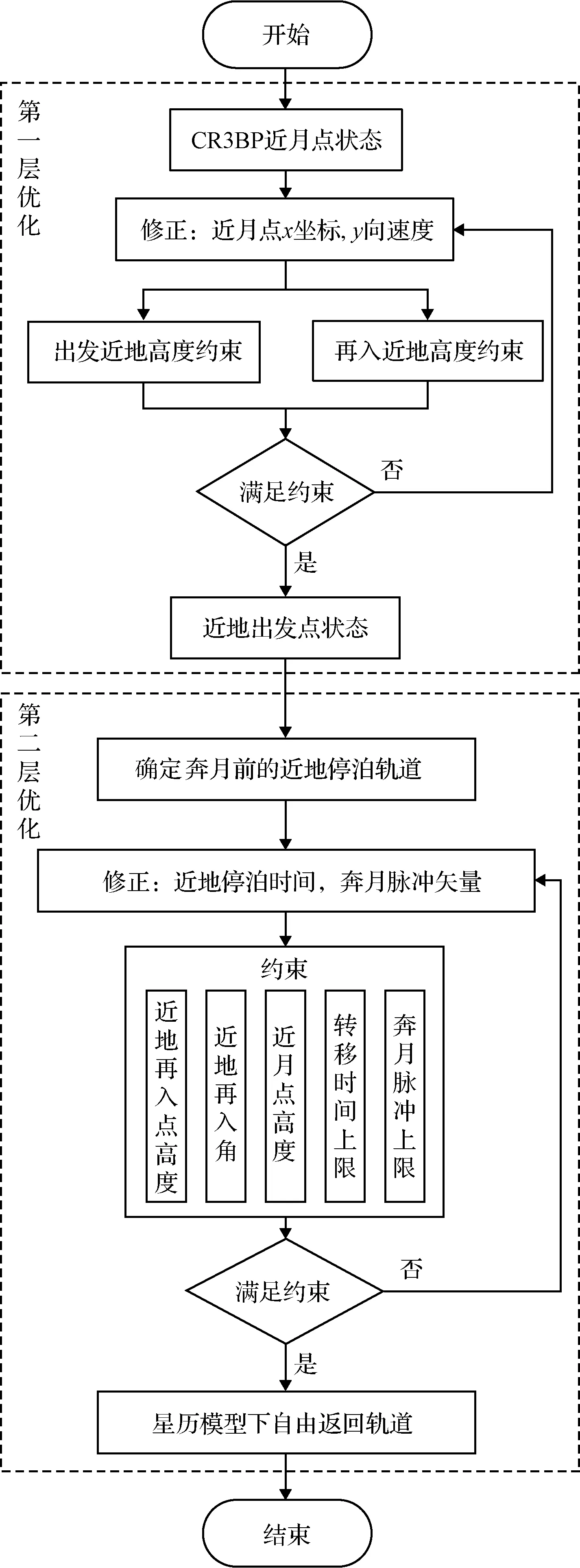
图6 两步优化修正策略流程图Fig.6 Flow chart of the two-step optimization-correction strategy

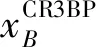
优化变量为

X=[xB,vyB]T

(21)

性能指标为

minJ=‖ΔVins‖

(22)

约束条件为

(23)

优化变量初值为

(24)

第二层优化修正在第一层优化修正后得到的近地出发点状态基础上进行。如图7所示，第一层优化结束后，在地月转移轨道的平面上可得到通过近地出发点(即图中的近地出发点I)的奔月前近地停泊圆轨道和所需的奔月脉冲ΔVinsI。

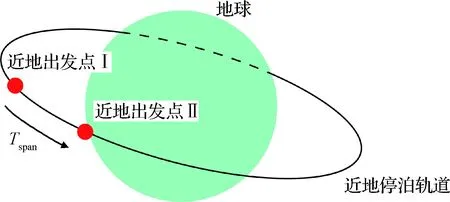
图7 近地停泊轨道示意图Fig.7 Schematic diagram of a low-Earth parking orbit

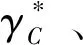
优化变量为

(25)

性能指标为

minJ=‖ΔVins‖

(26)

约束条件为

(27)

优化变量初值为

(28)

前述两层优化策略各层均是含约束非线性多变量函数优化问题，可采用常见的非线性规划方法进行求解。本文采用内点法[21]对第一层优化进行求解，内点法对初值敏感度低，内存使用量少，能够快速求解大型问题，适用于初值偏差较大且对求解速度要求高的第一层优化。由于第一层优化的结果相比于CR3BP下的结果已经进一步接近最终结果，因此在第二层优化时本文采用SQP方法[22]对第一层优化的结果进行局部寻优修正。

在星历模型下，当飞行器沿自由返回轨道到达近月点后，将二体模型下得到的三脉冲机动作为初值，在星历模型下利用SQP算法进行优化修正，优化约束为机动后的轨道参数，优化目标为燃料消耗最小，以此得到星历模型下的三脉冲机动策略。

SB0=[0.9929,0,0,0,-2.4447,0]T

第一层优化结束后，可得近地停泊轨道的初始点瞬时轨道根数为：近地点高度179.86 km、偏心率1×10-6、倾角24.51°、升交点赤经347.80°、近地点幅角314.09°、真近点角0°，地心惯性系下的奔月脉冲为

ΔVinsert1=[2640.45，1475.28，914.32]Tm/s

将第一层优化的结果作为初值，进行第二层优化，得到初始点到实际奔月出发点的时间Tspan=1.4 s，地心惯性系下的奔月脉冲为

ΔVinsert=[2641.17，1474.25，913.915]Tm/s

该算例求解得到的Tspan很小，说明该算例中第一层优化得到的近地出发点和实际出发点十分接近。当飞行器抵达近月点后实施三脉冲机动，进入倾角168.37°、升交点赤经86.8°的近月圆轨道。利用二体模型下给出的三脉冲机动如表1所示，星历模型下经过优化修正后的三脉冲机动结果如表2所示，而表3则给出了三脉冲经优化修正前后的环月轨道参数。结果显示，二体模型下给出的脉冲机动直接用于星历模型会导致最终的轨道参数与给定的轨道参数约束有所偏差，而将其作为初值在星历模型下进行优化修正后得到的三脉冲机动策略则能够很好地满足给定的目标轨道约束。图8给出了地心惯性系下的自由返回+三脉冲机动的全过程轨迹，图9给出了月心惯性系下三脉冲变轨前后的运动轨迹。

表1 二体模型下的近月三脉冲机动脉冲Table 1 Lunar three-pulse maneuvers under the two-body model

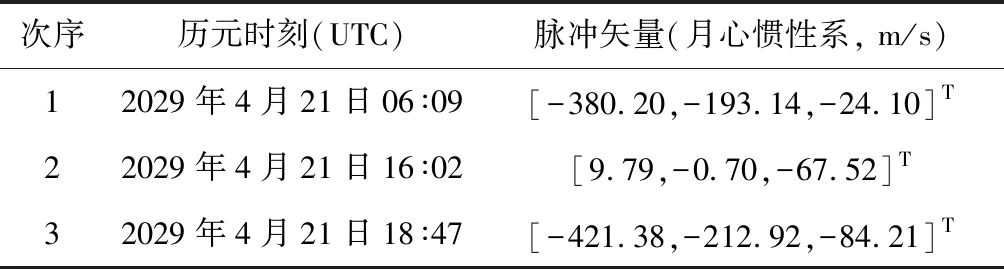
表2 星历模型下的近月三脉冲机动脉冲Table 2 Lunar three-pulse maneuvers under the ephemeris model

表3 三脉冲机动脉冲优化修正前后的轨道参数Table 3 Orbital elements after lunar three-pulse maneuvers with &without optimization and correction

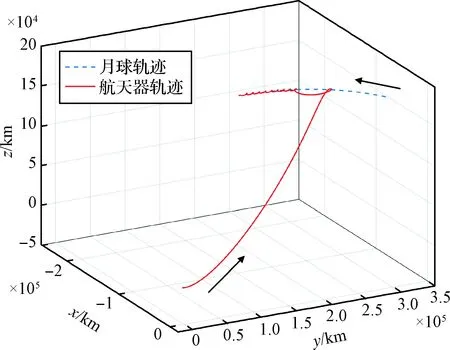
图8 地心惯性系下的全程地月转移轨迹Fig.8 Entire Earth-Moon transfer trajectory in the Earth-centered inertial coordinate system

图9 月心惯性系下的三脉冲变轨Fig.9 Lunar three-pulse maneuver in the Moon-centered inertial coordinate system

4 结 论

针对载人登月任务背景，本文提出了一种星历模型下的地月转移轨道设计方法。首先在圆型限制性三体模型下对地月空间内的自由返回轨道进行构造，之后在二体模型下对近月三脉冲变轨问题进行求解。提出了基于上述简化模型结果的两轮逐次优化修正策略，先后以高度和再入走廊约束为主约束,在星历模型下采用内点法和SQP算法对自由返回轨道进行优化修正，得到了星历模型下的自由返回+近月三脉冲变轨地月转移策略。仿真校验结果表明本文提出的方法能够在给定约束下有效求解星历模型下具备自由返回能力的地月转移轨道，为载人登月任务的转移轨道设计提供参考。