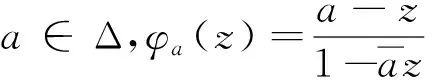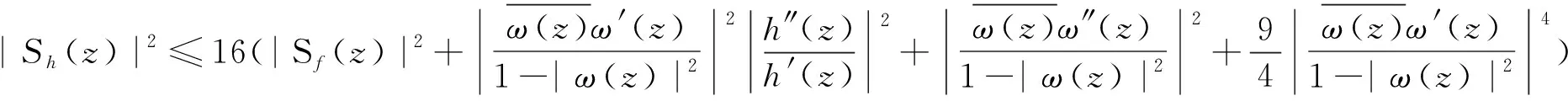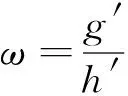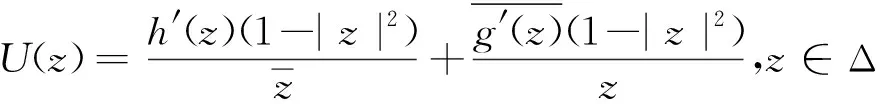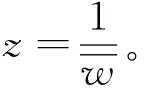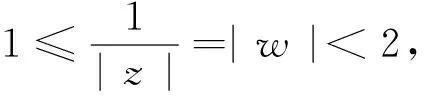单叶调和映射的Qp-拟共形延拓
2023-02-27陈艳林唐树安杨丛丽
陈 燚,陈艳林,唐树安,杨丛丽
(贵州师范大学 数学科学学院,贵州 贵阳 550025)
0 引言及主要的结果
为了叙述相关背景和结果,我们先从一些定义和记号开始。用Δ={z:|z|<1}表示全平面C上的单位圆盘,S1=∂Δ={z∈C:|z|=1}表示单位圆周,H(Δ)表示单位圆盘内的所有解析函数。设f(z)=u(x,y)+v(x,y)i是一个关于(x,y)的连续可微复值函数,其中u(x,y),v(x,y)分别是f(z)的实部和虚部,在z=x+yi,复值函数f的形式偏导数的定义为
其中fx=ux+vxi,fy=uy+vyi。如果单位圆盘内的一个复值函数f满足
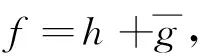
设k是一个非负实数且0≤k<1,f是区域Ω到Ω′的同胚映射,若f在Ω内具有ACL性质并且在Ω内几乎处处满足
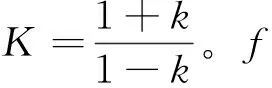
单位圆盘内的单叶函数的拟共形延拓理论与几何函数论、Teichmüller理论以及微分方程理论紧密相关,大量学者的研究得到了很多好的结果,并且这些结果得到了很好的应用,见文献[3-7]。然而,单位圆盘内单叶调和映射的拟共形延拓理论却是近些年才开始研究的,类似的单叶函数的拟共形映射的相关结果得到了推广和应用。

(1)
其中ω是f的第二复伸缩商。它的Schwarzian导数Sf的定义为
(2)

在文献[9]中,借助f的Pre-Schwarzian导数,Hernández和Martin证明了下列结果:

(3)
其中k满足
(4)
那么f在Δ内单叶且可以拟共形延拓至整个复平面C上。
文献[10]借助f的Schwarzian导数,相应地获得了下列结果:

|Sf(z)|(1-|z|2)2≤δ0t
(5)
则f在Δ内单叶且可以拟共形延拓至整个复平面C上,其中0≤t<1。
在文献[11]中,作者考虑了单叶调和映射能拟共形延拓且复伸缩商满足一定的Carleson测度条件的情形。我们首先给出Carleson测度的定义。设D=Δ或者D=Δ*:={z∈C:|z|>1},单位圆周S1上给一段弧I,Carleson集定义为:
其中|I|表示弧I的规范化长度,即
设0 那么称正测度λ为有界的p-Carleson测度,若 在文献[11]中,作者证明了下列结果: (6) 则下列陈述等价: A1:|Pf|2(1-|z|2)dxdy∈∈CM1(Δ) A2:|Sf|2(1-|z|2)3dxdy∈∈CM1(Δ) 此外,如果条件A1或者A2成立,则调和映射f在Δ内单叶且可以拟共形延拓至整个复平面C上,使得它的复伸缩商μ满足 本文将这一结果推广至p-Carleson测度情形。实际上,在单叶函数情形,Pua和Peláez证明了下列的结果: 定理4[12]设0 B1:|Pφ|2(1-|z|2)pdxdy∈CMp(Δ); B2:|Sφ|2(1-|z|2)p+2dxdy∈CMp(Δ)。 其中Pφ,Sφ为单叶函数经典的Pre-Schwarzian导数和Schwarzian导数。 对于紧的p-Carleson测度情形,Jin在文献[13]中证明了下列结果: 定理5[13]设0 C3:φ可以拟共形延拓至整个复平面C上,使得它的复伸缩商μ满足 本文将上述结果推广至单叶调和映射情形,主要结果如下: (7) 则下列陈述等价: D1:|Pf|2(1-|z|2)pdxdy∈CMp(Δ); D2:|Sf|2(1-|z|2)p+2dxdy∈CMp(Δ); 此外,若以上3个等价条件之一成立,则调和映射f在Δ内单叶且可以拟共形延拓至整个平面C上,使得它的复伸缩商μ满足 (8) 则下列陈述等价: E1:|Pf|2(1-|z|2)pdxdy∈CMp(Δ) E2:|Sf|2(1-|z|2)p+2dxdy∈CMp(Δ) 此外,如果条件E1或者E2成立,则调和映射f在Δ内单叶且可以拟共形延拓至整个平面C上,使得它的复伸缩商μ满足 当p=1时,所对应的结果为定理3。目前还不知道定理中的第二个结论的反向是否正确,由定理5可知,当f为共形映射时,在紧的Carleson测度情况下,第二结论反向是成立的。 这一小节将证明定理6。为此,需要下面准备。 其对应的小Qp空间定义为: Qp空间在文献[14-15]中被引入和研究。在文献[14]中作者证明了如果p>1,那么Qp空间就是Bloch空间,其中Bloch空间的定义如下: 关于Qp空间更多结果,请参考文献[16]。在文献[12]中,Pua等证明了: 定理7[12]假设0 F1:g=logφ′∈Qp; F2:|Sφ|2(1-|z|2)p+2∈CMp(Δ)。 其中φ为共形映射。注意当p>1时,Qp=B。 下面我们开始定理6的证明。 定理6的证明: (9) 其中k满足式(4)。因为h(z)是共形映射,所以由共形映射的理论知: (10) 根据调和映射f的Pre-Schwarzian导数和式(9)可知: (11) 根据式(7)可知: |Ph(z)|2(1-|z|2)pdxdy∈CMp(Δ) (12) 由定理4可知,式(12)等价于 |Sh|2(1-|z|2)p+2dxdy∈CMp(Δ) (13) 由(9)和(10)式,可以推出 (14) 由于ω是单位圆盘到自身的解析函数,由文献[17]中的结果可知,存在1个常数M>0,使得: (15) 因此由式(9)和式(15)可以推出: (16) 同理可得: (17) 根据调和映射f的Schwarzian导数可得: (18) 结合式(7)、式(13)、式(14)、式(16)和式(17),可推出: |Sf(z)|2(1-|z|2)2+pdxdy∈CMp(Δ), (19) 结合式(7)、式(14)、式(16)和式(17)可知,式(13)成立,再由定理4可知,式(13)等价于式(12)。根据调和映射f的Pre-Schwarzian导数可得: |Pf(z)|2(1-|z|2)p≤4(|Ph(z)|2(1-|z|2)p+ (20) 再结合式(7)和式(12),即可推出: |Pf|2(1-|z|2)pdxdy∈CMp(Δ), 综上,完成了D1⟺D2的证明。其次将完成D2⟺D3的证明,不妨假设D2成立,根据Schwarzian导数的定义以及式(7)、式(14)、式(16)和式(17),可以推出: |Sh|2(1-|z|2)p+2dxdy∈CMp(Δ) (21) 由于h为共形映射,所以根据定理7可知,式(21)等价于 (22) 即 (23) 由于p>1,所以可得出式(23)等价于 (24) 结合式(22)和式(24),可以推出: 反之,假设D3成立,根据Pre-Schwarzian导数的定义,有 即 结合式(24),可以推出式(22)成立,又因为h为共形映射,根据定理7可知: |Sh(z)|2(1-|z|2)p+2dxdy∈CMp(Δ), 根据Schwarzian导数的定义以及式(7)、式(13)、式(14)、式(16)和式(17),可以推出D2成立。这样我们完成了D2⟺D3的证明。 对第二部分的证明:不妨假设D1成立。则由文献[9]的定理2可知,f在Δ内单叶且可以拟共形延拓至整个复平面C上,该延拓函数为: 其中 如果|w|<1,则有|μF(w)|=|ω(w)|,所以由条件式(7)知: 和 根据复伸缩商的定义,我们有 (25) 另一方面,由于g″=(ωh′)′=ω′h′+ωh″,所以我们得到: 由于‖ω‖∞<1,根据式(3),于是可以推出: (26) 对于推论1的证明,其证明过程完全类似于定理6的证明过程。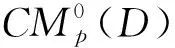

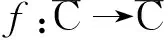
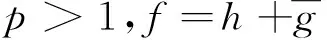

1 主要结果的证明