一个可抵抗关键词猜测攻击的可搜索加密方案

2023-02-27邓伦治

贵州师范大学学报（自然科学版） 2023年1期

王波,邓伦治

(贵州师范大学数学科学学院，贵州贵阳 550025)

0 引言

云存储服务由于其诸多优势(如数据可访问性、数据共享性等)提高了用户的体验质量，并且允许用户在任意地点远程访问云中的数据，因而被大量的公司或个人接受以减轻本地数据存储和管理的沉重负担。尽管云存储服务为用户提供了很多便利，但也面临很多问题和挑战。当用户将其敏感数据外包给云服务器后，在用户失去了有效控制数据能力的同时，云服务器和非法用户可以尝试获取数据中包含的信息，用户的隐私安全问题面临着巨大的挑战。为了保护敏感数据的安全，用户在外包之前通常会将数据加密。但是，当用户想要搜索某个数据时，如何搜索加密数据成为一个棘手的问题。

在2000年，由Song等[1]首先提出可搜索加密的概念，并且第一次提出了在密文上进行搜索的对称可搜索加密(Symmetric searchable encryption，SSE)方案，但是该方案存在密钥分配和检索效率较低的问题。2004年，由 Boneh 等[2]提出了第一个公钥可搜索加密(Public key encryption with keyword search，PEKS)方案，并将其运用到邮件路由的场景中。他们在方案中定义了IND-CKA (Indistinguishability against chosen keyword attack)安全模型，并证明了该方案的安全性。由于PEKS克服了SSE密钥分配的问题，因此PEKS更加适合数据分享的场景。在此之后，各种应用于区块链、物联网、智能电网、电子医疗和电子邮件系统等场景的PEKS方案被不断提出。

在 2006 年, Byun 等[3]发现当前的公钥可搜索加密体制存在严重的安全隐患:关键词往往是从一些小的关键词空间中选取出来(比如一些学科中的专业名词),因此攻击者通过发起离线关键词猜测攻击(Off-Line keyword guessing attacks)能够轻松获取关键词密文和搜索陷门中的关键词信息。2008年，Baek 等[4]提出了一个无安全信道的PEKS(Secure-channel-free PEKS,SCF-PEKS)方案，该方案移除了传统PEKS方案在关键词陷门传输过程中对安全信道的需求。然而，Yau等[5]指出在公共信道上传输的关键词陷门容易被一个外部敌手(通常指服务器和用户之外的实体)截取，外部敌手通过发起离线关键词猜测攻击可以揭露关键词陷门中的关键词信息，并对Baek 等[4，6]提出的两个方案进行了详细的离线关键词猜测攻击分析。

为了抵御由外部敌手发起的离线关键词猜测攻击,在 2009年，Rhee 等[7]提出了一种指定测试者的可搜索加密 (Searchable public key encryption with a designated tester，DPEKS)方案, 方案中的匹配算法只能由指定的服务器来执行。该方案还引入了陷门不可区分(Trapdoor indistinguishability)的概念, 加强了PEKS方案中的陷门安全。后来，Rhee 等[8]又提出了一个变体方案，该方案可以抵抗由外部敌手发起的离线关键词猜测攻击。然而，不久之后， Hu等[9-10]指出文献[7-8]的方案无法抵御由恶意服务器发起的离线关键词猜测攻击，并提出了相应的改进方案。之所以会发起该攻击，原因是执行匹配算法的服务器往往是“诚实且好奇”的，即服务器会按照用户的指令执行操作，但也会对用户数据 “感兴趣”。在2013年，Yau等[11]对关键词猜测攻击进行了更深层次的研究，提出了一种称为“在线关键词猜测攻击(On-Line keyword guessing attacks)”的新攻击方式。该攻击之所以能够实现，主要原因是只有公钥参与关键词加密算法或陷门生成算法，使得任意一个敌手都可以假冒成数据拥有者或用户去生成关键词密文或陷门。

2015年，基于双服务器的公钥可搜索加密(Dual-server PEKS，DS-PEKS)方案被Chen等[12]提出。在该方案安全模型中，前服务器(Front Server)与后服务器(Back server)都是“半诚实”的，但两者不能串谋。虽然基于两个服务器的模型可以增强方案安全性，不能串谋的条件也使得方案看似可以抵抗来自内部敌手的关键词猜测攻击，但是该方案的关键词加密算法与陷门生成算法都是使用前服务器与后服务器的公钥加密，所以任意一个敌手依然可以实施在线关键词猜测攻击。后来，Huang等[13]指出了Chen等[12]的方案的缺陷，同时提出了一个新的DS-PEKS方案，并声称新方案能够抵抗来自内部敌手的关键词猜测攻击。虽然该方案的安全模型中假定至少有一个服务器是“诚实”的，但遗憾的是，Huang等[13]提出的方案和文献[12]的方案一样，在关键词加密算法与陷门生成算法中都是使用服务器的公钥加密，所以一个恶意的内部敌手仍然可以发起在线关键词猜测攻击。与此同时，黄海平等[14]也提出了一个“基于云存储的多服务器多关键词可搜索加密方案”，该方案中需要将密文文档按照某种规则等分成N份分别发送给N个服务器。虽然该方案可以抵抗在线关键词猜测攻击，但是该方案需要安全信道去传输密钥，且计算成本较高。

考虑到只有公钥参与关键词密文生成算法或陷门生成算法是在线关键词猜测攻击得以实施的原因，因此，如果想要成功抵抗在线关键词猜测攻击，关键词密文生成算法与陷门生成算法都必须使用私钥。2018年，Huang等[15]提出了一个公钥认证可搜索加密(Public-key authenticated encryption with keyword search，PAEKS)方案，该方案加入了认证功能：关键词密文需要数据拥有者的私钥来生成，其他个体不能伪造出该数据拥有者才能生成的有效关键词密文，这一性质对于用户生成陷门也一样。结果表明，该方案可以成功抵抗在线关键词猜测攻击。2019年，Chen等[16]提出了一个基于双服务器的公钥认证可搜索加密(Dual-server public-key authenticated encryption with keyword search，DPAEKS)方案。该方案是基于两个不能串谋的双服务器模型，同样可以成功抵抗在线关键词猜测攻击。与此同时，张玉磊等[17]提出一个基于多服务器的密钥聚合可搜索加密方案。虽然该方案可以抵抗在线关键词猜测攻击，但是需要安全信道去传输加密钥和授权密钥；Lu等[18]提出了一个可抵抗两类关键词猜测攻击的DPEKS方案一般构造方法，该方案的关键一步是：利用Diffie-Hellman密钥协商方案，数据拥有者和用户之间可以得到一个相同的密钥，该密钥只有两者知道，这就相当于数据拥有者和用户之间在没有使用安全信道的条件下就得到了一个对称密钥,同时实现了认证功能； Lu等[19]还将关键词猜测攻击分为3种类型(来自外部敌手的离线关键词猜测攻击、来自外部敌手的在线关键词猜测攻击和来自内部敌手的离线关键词猜测攻击)，并提出了一个应用于电子医疗记录的PEKS方案，该方案在标准模型下被证明实现了关键词密文不可区分性和陷门不可区分性。同时，Lu等[20-21]又提出2个新的PEKS方案，且方案[21]适用于计算能力有限的场景，并在新的安全模型下证明了安全性。后来，Qin等[22]提出了一个PAEKS方案，并在新的安全模型下实现了“多密文”不可区分性。在该方案安全模型的挑战阶段，敌手会挑选2个关键词组发送给挑战者，挑战者也会随机对某一个关键词组中所有关键词加密来生成挑战密文，这是与其它方案的安全模型最显著的区别。杨宁滨等[23]提出了一个无配对公钥可搜索加密方案，也实现了多关键词密文不可区分性；郭丽峰等[24]提出了一个SCF-PEKS方案,但是由于关键词加密算法是用公钥加密，并没有私钥参与，所以并不能有效抵抗在线关键词猜测攻击。在2021年，陈宁江等[25]提出了一个可以抵御内部关键字猜测攻击的PEKS方案，该方案引入了一种叫做“倒排索引”的技术，并实现次线性搜索，其搜索效率只与包含相关查询关键字的密文数成正比。与此同时，Nayak等[26]也提出了一个PEKS方案，该方案需要指定的服务器执行匹配算法且可以抵抗关键词猜测攻击； Pan等[27]提出了一个实现多密文不可区分性与多陷门不可区分性的PEKS方案；Zhang等[28]提出了一个可以实现搜索由其他用户或自己分享的加密邮件的PEKS方案；郑东等[29]提出了一个基于区块链的多用户环境下的可搜索加密方案，该方案基于判定性双线性 Diffie-Hellman 假设和修改的判定性双线性 Diffie-Hellman 假设被证明可以抵御内部关键词猜测攻击；张键红等[30]提出了一个云环境下安全的可验证多关键词搜索加密方案，该方案虽然实现了数据完整性验证的功能并且能够抵抗关键词猜测攻击，然而该方案中的用户只能搜索自己的数据，没有实现搜索他人数据的功能。

本文提出了一个可以抵抗关键词猜测攻击的可搜索加密方案。该方案具有以下特点：

1)本文提出的方案在随机预言模型下实现了关键词密文的不可区分性、陷门的不可区分性、关键词密文的不可伪造性与陷门的不可伪造性。关键词密文的不可区分性与陷门的不可区分性保证了方案可以抵抗由外部敌手发起的离线关键词猜测攻击；关键词密文的不可伪造性与陷门的不可伪造性保证了方案可以抵抗由外部敌手发起的在线关键词猜测攻击；而以上4种安全性质保证了方案可以抵抗由内部敌手发起的离线关键词猜测攻击。总之，我们的方案可以抵抗现已知的3种关键词猜测攻击。

2)关键词加密算法和陷门生成算法都没有使用双线性对，这使得数据发送者和接收者只需承担较低的计算成本。

1 预备知识

1.1 双线性映射

定义1(双线性映射[19]):设G1和G2是两个p阶循环群，p是素数，g是G1的生成元。映射e:G1×G1→G2是满足以下性质的双线性映射：

2)非退化性:e(g，g)≠1;

1.2 困难问题

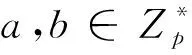
2 系统框架与安全模型

2.1 系统模型

我们方案的系统模型包括4个参与方：可信中心、发送者、接收者以及云服务器(图1)。

图1 系统模型Fig.1 System model

1)可信中心：可信中心主要负责生成和发布系统参数。

2)发送者：发送者先对关键词进行加密，生成索引，然后将加密后的数据以及索引发送给云服务器。

3)接收者：接收者生成关键词陷门，发送给云服务器，并将从云服务器接收到的数据进行解密。

4)云服务器：服务器收到由接收者发送的关键词陷门后，执行测试算法并将满足检索条件的数据发送给接收者。

2.2 方案框架

本文提出的方案由以下算法构成：

· Global Setup (λ)：输入安全参数λ，算法输出全局参数GP。

· KenGen(GP)：输入GP, 算法输出发送者和接收者的公、私钥对(skS,pkS)和(skR,pkR)。

· PEKS (GP,skS,pkR,w):输入GP,发送者的私钥skS,接收者的公钥pkR和关键词w,算法计算关键词密文Cw。

· Trapdoor (GP,skR,pkS,w′)输入GP,发送者的公钥pkS,接收者的私钥skR和关键词w′,算法计算关键词陷门Tw′。

· Test (GP,Cw,Tw′): 输入GP,关键词密文Cw和关键词陷门Tw′,算法测试等式是否成立：若等式成立输出1，否则输出0。

参数详情见表1。

表1 符号及其意义Tab.1 Symbol and its meaning

2.3 安全模型

在本文中，我们要求提出的方案满足关键词密文的不可区分性、陷门的不可区分性、关键词密文的不可伪造性和陷门的不可伪造性，并以游戏的方式定义安全模型。其中，关键词密文的不可区分性和陷门的不可区分性保证了方案可以抵抗由外部敌手发起的离线关键词猜测攻击；关键词密文的不可伪造性和陷门的不可伪造性保证了方案可以抵抗由外部敌手发起的在线关键词猜测攻击；而以上4种安全性质保证了方案可以抵抗由内部敌手发起的离线关键词猜测攻击。总之，我们的方案可以抵抗现已知的3种关键词猜测攻击。

游戏1关键词密文的不可区分性

设置给定安全参数λ,挑战者C生成全局参数GP,然后将参数GP发送给敌手A。

阶段1 在此阶段，多项式时间敌手A适应性地查询以下预言机：

Opk查询：当敌手A提交1个身份IDi,挑战者C返回公钥pki给敌手A；

Osk查询：当敌手A提交1个身份IDi,挑战者C返回私钥ski给敌手A；

OC查询：当敌手A提交2个身份(IDi,IDj)和1个关键词w,挑战者C返回发送者身份为IDi而接收者身份为IDj的、关于关键词w的密文Cw；

OT查询：当敌手A提交2个身份(IDi,IDj)和1个关键词w,挑战者C返回发送者身份为IDi而接收者身份为IDj的、关于关键词w的陷门Tw；

OM查询：敌手A提交1个关键词密文Cw和1个关键词陷门Tw′,挑战者C返回Test (GP,Cw,Tw′)的结果。

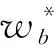
定义2 如果概率多项式时间敌手A赢得游戏1的优势是可以忽略的，则称该方案满足关键词密文的不可区分性。

游戏2 陷门的不可区分性

设置同游戏1。

阶段1 同游戏1。

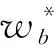
定义3 如果概率多项式时间敌手A赢得游戏2的优势是可以忽略的，则称该方案满足陷门的不可区分性。

游戏3 关键词密文的不可伪造性

设置同游戏1。

阶段1 同游戏1。

挑战敌手A输出2个身份(IDi*,IDj*)和关键词w*的伪造密文Cw*发送给挑战者C,这里要求敌手A没有对(IDi*,IDj*,w*)进行过OC查询。随后，C对(IDi*,IDj*,w*)进行OT查询，并获得关键词w*的陷门Tw*。最后，挑战者C对(Cw*,Tw*)进行OM查询，可以得到结果0或1。如果OM输出结果为1，则敌手A获胜。定义敌手A赢得这一游戏的优势为Adv(A)=|Pr[OM→1]|。

定义4 如果概率多项式时间敌手A赢得游戏3的优势是可以忽略的，则称该方案满足关键词密文的不可伪造性。

游戏4 关键词陷门的不可伪造性

设置同游戏1。

阶段1 同游戏1。

挑战敌手A输出2个身份(IDi*,IDj*)和关键词w*的伪造陷门Tw*发送给挑战者C,这里要求敌手A没有对(IDi*,IDj*,w*)进行过OT查询。随后，C对(IDi*,IDj*,w*)进行OC查询，并获得关键词w*的密文Cw*。最后，挑战者C对(Cw*,Tw*)进行OM查询，可以得到结果0或1。如果OM输出结果为1，则敌手A获胜。定义敌手A赢得这一游戏的优势为Adv(A)=|Pr[OM→1]|。

定义5 如果概率多项式时间敌手A赢得游戏4的优势可以忽略的，则称该方案满足陷门的不可伪造性。

3 提出的方案

3.1 方案构造

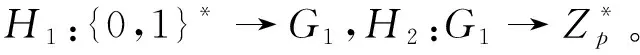
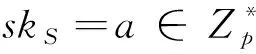
Cw=(C1,C2)=(C1=H1(w)kgr,C2=hr)

其中k=H2((pkR)skS)=H2((gb)a)=H2(gab)。

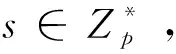
Tw′=(T1,T2)=(T1=(H1(w′)k)-1gs,T2=hs)

其中k=H2((pkS)skR)=H2((ga)b)=H2(gab)。

· Test (GP,Cw,Tw′): 输入GP,关键词密文Cw=(C1,C2)和关键词陷门Tw′=(T1,T2),算法测试等式

e(C1·T1,h)=e(g,C2·T2)

如果等式成立，则输出1;否则，输出 0。

3.2 安全性分析

定理1 在随机预言模型下，若 HDH问题是困难的，则该方案满足关键词密文的不可区分性。

给定HDH问题实例(g,ga,gb,X),C将扮演游戏中的挑战者去判断X=H2(gab)是否成立。

设置输入安全参数λ,C通过Global Setup (λ) 算法生成系统参数GP={p,G1,G2,e,g,h,H1,H2},然后将参数GP发送给A。

阶段1敌手A将在多项式时间内进行以下查询。不失一般性，假定每次查询互不相同，且在没有进行Opk查询前不能进行其它查询。

Opk查询：C以的格式设置列表Lpk。当敌手A输入IDi时，C查找列表Lpk,若已经存在于列表Lpk,则返回pki；否则，C按照如下方式进行回应：

若i=I,C将=添加进列表Lpk,并返回pkI给A；

若i=J,C将=添加进列表Lpk,并返回pkJ给A；

Osk查询：C以的格式设置列表Lsk。当敌手A输入IDi时，若i=I或者i=J,则游戏终止；否则，C查找列表Lsk,并返回ski给A。

H1查询:C以的格式设置列表L1。当敌手A输入w时，若已经存在于列表L1,则返回h1；否则，C随机选取h1∈G1,将保存至列表L1,并把H1(w)=h1返回给敌手A。

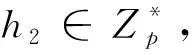
Cw=(C1,C2)=(C1=H1(w)X*gr,C2=hr)

其中，X*的取值如表2所示。

Tw=(T1,T2)=(T1=(H1(w)X*)-1gs,T2=hs)

其中，X*的取值如表2所示。

表2 X*的值Tab.2 The value of X*

OM查询：敌手A提交1个关键词密文Cw和1个关键词陷门Tw′,挑战者C返回Test (GP,Cw,Tw′)的结果。

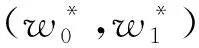
如果{i*,j*}≠{I,J},游戏终止；

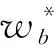
当X≠H2(gab),那么当b=0或b=1时，密文各部分具有相同的概率分布。因而A在区分b上不具有任何的优势。所以

因此:

概率分析设事件E1：在阶段1游戏终止；事件E2：挑战阶段游戏终止；事件E：游戏终止。则

定理2在随机预言模型下，如果HDH问题是困难的，那么我们的方案满足关键词陷门的不可区分性。

给定HDH问题实例(g,ga,gb,X),C将扮演游戏中的挑战者去判断X=H2(gab)是否成立。

设置输入安全参数λ,C通过Global Setup (λ) 算法生成系统参数GP={p,G1,G2,e,g,h,H1,H2},然后将参数GP发送给A。

阶段1敌手A可以进行H1、H2、Opk、Osk、OC、OT和OM查询，挑战者C按照定理1中相同的方式回应。

如果{i*,j*}≠{I,J},游戏终止；

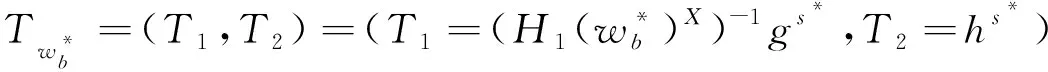
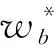
因此:

概率分析设事件E1：在阶段1游戏终止；事件E2：挑战阶段游戏终止；事件E：游戏终止。则

定理3 在随机预言模型下，如果HDH问题是困难的，那么我们的方案满足关键词密文的不可伪造性。

给定HDH问题实例(g,ga,gb,X),C将扮演游戏中的挑战者去判断X=H2(gab)是否成立。

设置输入安全参数λ,C通过Global Setup (λ) 算法生成系统参数GP={p,G1,G2,e,g,h,H1,H2},然后将参数GP发送给A。

阶段1敌手A可以进行H1、H2、Opk、Osk、OC、OT和OM查询，挑战者C按照定理1中相同的方式回应。

挑战敌手A输出2个身份(IDi*,IDj*)和关键词w*的伪造密文Cw*发送给挑战者C,这里要求敌手A没有对(IDi*,IDj*,w*)进行过OC查询。挑战者C按照如下方式回应：

如果{i*,j*}≠{I,J},游戏终止；

如果{i*,j*}={I,J},则C对(IDi*,IDj*,w*)进行OT查询，并获得关键词w*的陷门Tw*。然后，挑战者C对(Cw*,Tw*)进行OM查询，可以得到结果0或1。如果输出结果为1，则挑战者C返回1，即此时有X=H2(gab)；否则，挑战者C返回0。

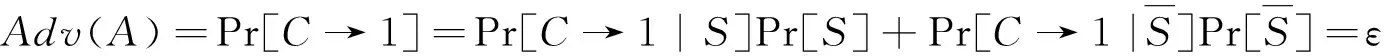
概率分析假设事件E1：在阶段1游戏终止；事件E2：挑战阶段游戏终止；事件E：游戏终止。则

定理4 在随机预言模型下，如果HDH问题是困难的，那么我们的方案满足关键词陷门的不可伪造性。

给定HDH问题实例(g,ga,gb,X),C将扮演游戏中的挑战者去判断X=H2(gab)是否成立。

设置输入安全参数λ,C通过Global Setup (λ) 算法生成系统参数GP={p,G1,G2,e,g,h,H1,H2},然后将参数GP发送给A。

阶段1 敌手A可以进行H1、H2、Opk、Osk、OC、OT和OM查询，挑战者C按照定理1中相同的方式回应。

挑战敌手A输出2个身份(IDi*,IDj*)和关键词w*的伪造陷门Tw*发送给挑战者C,这里要求敌手A没有对(IDi*,IDj*,w*)进行过OT查询。挑战者C按照如下方式回应：

如果{i*,j*}≠{I,J},游戏终止；

如果{i*,j*}={I,J},则C对(IDi*,IDj*,w*)进行OC查询，并获得关键词w*的密文Cw*。然后，挑战者C对 (Cw*,Tw*)进行OM查询，可以得到结果0或1。如果输出结果为1，则挑战者C返回1，即此时有X=H2(gab)；否则，挑战者C返回0。

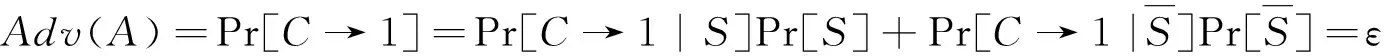
概率分析设事件E1：在阶段1游戏终止；事件E2：挑战阶段游戏终止；事件E：游戏终止。则

4 性能分析

4.1 安全性比较

在表3，我们将本文提出的方案与几个已经提出的公钥可搜索加密方案作一个安全性对比，对比项目主要包括该方案是否能够抵抗现已知的3种关键词猜测攻击：KGAI: 来自外部敌手的离线关键词猜测攻击; KGAII: 来自外部敌手的在线关键词猜测攻击; KGAIII: 来自内部敌手的离线关键词猜测攻击。为了简便，我们使用“是”表示该行所对应的方案可以抵抗该列所对应的关键词猜测攻击，“否”则表示该行所对应的方案不能够抵抗该列所对应的关键词猜测攻击。

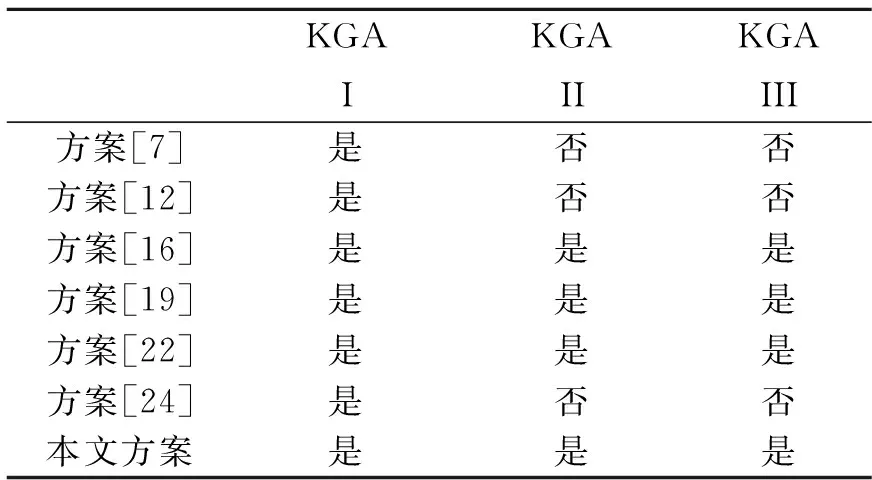
表3 安全性对比Tab.3 Security comparison

4.2 计算成本比较

为了公平，我们使用Lu等[19]的第三方实验数据，该数据是在配置为Interl(R) CoreTMi3-2310M CPU@2.10 GHz 和 4 GB RAM 内存的笔记本电脑上运行得到，而基准时间是通过利用PBC(Pairing-based cryptography)库[31]获得。为了实现1 024比特RSA的安全级别，Lu等[19]使用定义在超奇异椭圆曲线E(Fq):y2=x3+x的Type-A配对，并选择SHA-1作为一般Hash函数。在效率比较上，我们同样只考虑关键词加密算法、陷门生成算法和测试算法的计算成本。其中，计算成本的比较主要考量以下4种运算造成的计算成本：双线性对计算成本(TBP)、映射到群G1的哈希函数计算成本(THP)、群G1上的幂运算成本(TE1)和群G2上幂运算成本(TE2)。由文献[19]，这4种计算单次运行时间分别是2.486 ms,0.334 ms,0.311 ms和0.059 ms。于是，在我们的方案中，执行一次关键词加密算法的计算成本是：0.334+4×0.311=1.578 ms；执行一次陷门生成算法的计算成本是：0.334+4×0.311=1.578 ms；执行一次测试算法的计算成本是：2×2.486=4.972 ms。同理，可以求出其它方案分别执行一次关键词加密算法、陷门生成算法和测试算法的计算成本，并由此得到表4和图2。由表4或图2可知，与其它使用双线性对的可搜索加密方案相比，本文提出方案的关键词加密算法和陷门生成算法只需要较低的计算成本。为了更加直观与符合实际情况，我们将各个方案的关键词加密算法和陷门生成算法分别执行多次来比较2个算法的计算成本，得到图3和图4。其中，横轴表示算法执行次数，纵轴表示运行时间。